13.1.2线段的垂直平分线的性质 教案 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 13.1.2线段的垂直平分线的性质 教案 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 619.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 20:11:49 | ||
图片预览




文档简介
第十三章 轴对称
·13.1.2 线段的垂直平分线的性质·
教案
班级: 课时: 课型:
学情分析
学生在上一课时的探究中,得出了线段的垂直平分线的概念,对其性质有初步的认识,但未利用公理及其推导出的定理进行证明,因此不够严谨.垂直平分线的性质定理在日后学习几何图形的研究中占据一定的地位,因此要求学生理解并掌握.
二、教学目标
1.掌握线段的垂直平分线的性质定理及判定定理.
2.会利用线段的垂直平分线的性质和判定进行简单的推理.
三、重点难点
【教学重点】
线段垂直平分线的性质和判定及其应用.
【教学难点】
灵活运用线段的垂直平分线的性质和判定进行推理.
四、教学过程设计
第一环节 【复习旧知 引入新课】
师生共同回顾旧知:
如果一个平面图形沿一条直线 折叠 ,直线两旁的部分能够 互相重合 ,这个图形就叫做轴对称图形.这条直线就是它的 对称轴 .
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形 关于这条直线(成轴)对称 .这条直线叫做 对称轴 ,折叠后重合的点是对应点,叫做 对称点 .
设计意图:通过复习轴对称的有关知识,为本课的学习做好知识储备,减小学习难度.
第二环节 【合作交流 探索新知】
如图,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到点A与点B的距离,你有什么发现?
学生独立思考,发现P1A=P1B,P2A=P2B,P3A=P3B.
因此得出猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
师生共同求证:
求证:线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC=CB.点P在l上.
求证:PA=PB.
证明:∵l⊥AB,
∴∠PCA=∠PCB.
又AC=CB,PC=PC,
∴△PCA≌△PCB(SAS).
∴PA=PB.
归纳:线段的垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵AC=BC,l⊥AB,点P在l上,
∴PA=PB.
师:反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
猜想:与线段两个端点距离相等的点在这条线段的垂直平分线上.(教师引导学生类比前面的探究证明这个猜想)
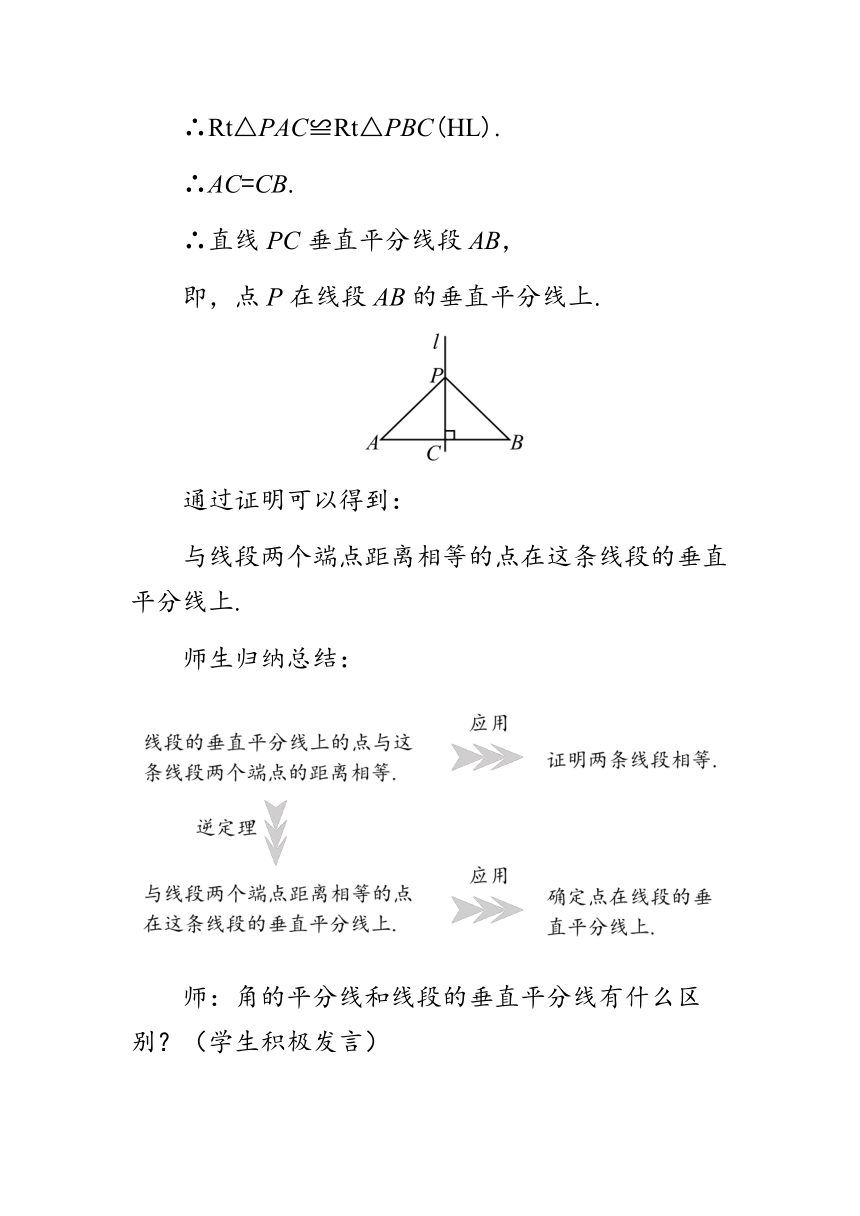
如图,若PA=PB,你能说明点P在线段AB的垂直平分线上吗?
证明:过点P作PC⊥AB于C,
∴∠PCA=∠PCB=90°.
在Rt△PAC和Rt△PBC中,
∴Rt△PAC≌Rt△PBC(HL).
∴AC=CB.
∴直线PC垂直平分线段AB,
即,点P在线段AB的垂直平分线上.
通过证明可以得到:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
师生归纳总结:
师:角的平分线和线段的垂直平分线有什么区别?(学生积极发言)
设计意图:通过观察、思考,让学生自主探究出垂直平分线的定义,在教师的指引下,学生动手实践分析总结出图形轴对称的性质,推理得到线段垂直平分线的性质的判定,展现以学生为主体的教学理念.
第三环节 【应用迁移 巩固提高】
例1.如图,AB=AC,MB=MC.直线AM是线段BC的垂直分线吗?并说明理由.
例2.尺规作图:经过已知直线外一点作这条直线的垂线.
例3.如图,在△ABC中,已知AC=27,DE垂直平分AB,交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
设计意图:通过例题的教学,让学生能够运用所学知识解决问题,激发学生学习的积极性.
【答案】
例1.解:直线AM是线段BC的垂直平分线.
理由如下:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
例2.已知:直线AB和AB外一点C.(如图)
求作:AB的垂线,使它经过点C.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,
交AB于点D和点E.
(3)分别以点D和点E为圆心,大于DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求作的垂线.
例3.解:∵ 点E在BA的垂直平分线上,
∴ AE=BE.
∵ △BCE的周长=BC+CE+BE=50,
∴ BC+CE+AE=BC+AC=50.
∵ AC=27,
∴ BC=23.
第四环节 【随堂练习 巩固新知】
1.(2019秋 蓝山县期中)下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(2020 和平区校级模拟)如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
3.(2019秋 大冶市期末)如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=10cm,则△EBC的周长为( )
A.16cm B.18cm C.26cm D.28cm
4.(2019秋 清江浦区期末)如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A的度数为( )
A.31° B.62° C.87° D.93°
5.(2019秋 孟津县期末)如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,AE=7cm,AP=4cm,则P点到直线AB的距离是 .
设计意图:本环节为基础练习,目的在于考察学生对线段的垂直平分线的性质的理解程度.
【答案】
C 2.B 3.B 4.C 5.3cm.
第五环节 【当堂检测 及时反馈】
1.(2019 梧州)如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
2.(2019秋 博山区期中)如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC B.PB=PC
C.PB<PC D.PB=2PC
3.(2019 雁塔区校级模拟)如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
4.如图,△ABC中,DG垂直平分AB交AB于点D,交BC于点M,EF垂直平分AC交AC于点E,交BC于点N,且点M在点N的左侧,连接AM、AN,若BC=12cm,则△AMN的周长是( )
A.10 cm B.12 cm C.14 cm D.16 cm
5.(2020春 北镇市期中)如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BD于点E,连接CE,若∠A=60°,∠ACE=24°,则∠ABE的度数为( )
A.24° B.30° C.32° D.48°
6.(2019秋 平果县期末)如图,在△ABC中,DH是AC的垂直平分线,交BC于点P,MN是AB的垂直平分线,交BC于点O,连接AP、AQ,已知∠BAC=72°,则∠PAQ= .
7.(2019秋 息县期末)如图,BD垂直平分AG于D,CE垂直平分AF于E,若BF=1,FG=3,GC=2,则△ABC的周长为 .
8.(2019秋 三台县期末)如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,则△ABC的面积是 cm2.
9.(2019秋 浏阳市期末)如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,求证:AD垂直平分EF.
10.(2019秋 泰兴市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
求∠DAF的度数;
若△DAF的周长为10,求BC的长.
设计意图:通过本环节练习,锻炼学生的思维,考察学生能否灵活应用本课知识进行求解,突出本课重点.
【答案】
B 2.B 3.D 4.B 5.C
6.36°. 7.15. 8.24.
9.证明:设AD、EF的交点为K,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF.
∴AD是线段EF的垂直平分线.
10.解:(1)∠BAC=180°-∠ABC-∠ACB
=180°-30°-50°=100°,
∵DE是AB的垂直平分线,∴DA=DB,
∴∠DAB=∠ABC=30°,
∵FG是AC的垂直平分线,∴FA=FC,
∴∠FAC=∠ACB=50°,
∴∠DAF=∠BAC-(∠DAB+∠FAC)=20°;
(2)∵△DAF的周长为10,
∴AD+DF+FC=10,
∴BC=BD+DF+FC=AD+DF+FC=10.
第六环节 【拓展延伸 能力提升】
1.(2019秋 莱西市期中)如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
2.如图,OE,OF分别是△ABC中AB,AC边的中垂线(即垂直平分线),∠OBC、∠OCB的平分线相交于点I,试判定OI与BC的位置关系,并给出证明.
设计意图:本环节的目的在于拓展学生的知识面,展现有梯度的教学理念.
【答案】
1.解:(1)当x=5时,点E在线段CD的垂直平分线上,
理由是:当x=5时,AE=2×5cm=10cm=BC,
∵AB=25cm,DA=15cm,CB=10cm,
∴BE=AD=15cm,
在△ADE和△BEC中,
∴△ADE≌△BEC(SAS),
∴DE=CE,
∴点E在线段CD的垂直平分线上,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-(∠AED+∠CEB)=90°,
∴DE⊥CE.
2.解:OI⊥BC.
理由:连接OA,过点I作IM⊥OB于点M,过点I作IN⊥OC于点N,过点I作IG⊥BC于点G,
∵OE,OF分别是AB,AC边的中垂线,
∴OA=OB,OA=OC,
∴OB=OC,
∵∠OBC,∠OCB的平分线相交于点I,
∴IM=IG,IN=IG,
∴IM=IN,
∴点I在∠BOC的角平分线上,
∵OB=OC,
∴OI⊥BC.
第七环节 【总结反思 知识内化】
设计意图:通过小结,使学生梳理本节课所学内容,突出重点.
第八环节 【布置作业 夯实基础】
·13.1.2 线段的垂直平分线的性质·
教案
班级: 课时: 课型:
学情分析
学生在上一课时的探究中,得出了线段的垂直平分线的概念,对其性质有初步的认识,但未利用公理及其推导出的定理进行证明,因此不够严谨.垂直平分线的性质定理在日后学习几何图形的研究中占据一定的地位,因此要求学生理解并掌握.
二、教学目标
1.掌握线段的垂直平分线的性质定理及判定定理.
2.会利用线段的垂直平分线的性质和判定进行简单的推理.
三、重点难点
【教学重点】
线段垂直平分线的性质和判定及其应用.
【教学难点】
灵活运用线段的垂直平分线的性质和判定进行推理.
四、教学过程设计
第一环节 【复习旧知 引入新课】
师生共同回顾旧知:
如果一个平面图形沿一条直线 折叠 ,直线两旁的部分能够 互相重合 ,这个图形就叫做轴对称图形.这条直线就是它的 对称轴 .
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形 关于这条直线(成轴)对称 .这条直线叫做 对称轴 ,折叠后重合的点是对应点,叫做 对称点 .
设计意图:通过复习轴对称的有关知识,为本课的学习做好知识储备,减小学习难度.
第二环节 【合作交流 探索新知】
如图,直线l垂直平分线段AB,P1,P2,P3,…是l上的点,分别量一量点P1,P2,P3,…到点A与点B的距离,你有什么发现?
学生独立思考,发现P1A=P1B,P2A=P2B,P3A=P3B.
因此得出猜想:线段垂直平分线上的点与这条线段两个端点的距离相等.
师生共同求证:
求证:线段垂直平分线上的点与这条线段两个端点的距离相等.
已知:如图,直线l⊥AB,垂足为C,AC=CB.点P在l上.
求证:PA=PB.
证明:∵l⊥AB,
∴∠PCA=∠PCB.
又AC=CB,PC=PC,
∴△PCA≌△PCB(SAS).
∴PA=PB.
归纳:线段的垂直平分线的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等.
符号语言:
∵AC=BC,l⊥AB,点P在l上,
∴PA=PB.
师:反过来,如果PA=PB,那么点P是否在线段AB的垂直平分线上呢?
猜想:与线段两个端点距离相等的点在这条线段的垂直平分线上.(教师引导学生类比前面的探究证明这个猜想)
如图,若PA=PB,你能说明点P在线段AB的垂直平分线上吗?
证明:过点P作PC⊥AB于C,
∴∠PCA=∠PCB=90°.
在Rt△PAC和Rt△PBC中,
∴Rt△PAC≌Rt△PBC(HL).
∴AC=CB.
∴直线PC垂直平分线段AB,
即,点P在线段AB的垂直平分线上.
通过证明可以得到:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
师生归纳总结:
师:角的平分线和线段的垂直平分线有什么区别?(学生积极发言)
设计意图:通过观察、思考,让学生自主探究出垂直平分线的定义,在教师的指引下,学生动手实践分析总结出图形轴对称的性质,推理得到线段垂直平分线的性质的判定,展现以学生为主体的教学理念.
第三环节 【应用迁移 巩固提高】
例1.如图,AB=AC,MB=MC.直线AM是线段BC的垂直分线吗?并说明理由.
例2.尺规作图:经过已知直线外一点作这条直线的垂线.
例3.如图,在△ABC中,已知AC=27,DE垂直平分AB,交AB于点D,交AC于点E,△BCE的周长等于50,求BC的长.
设计意图:通过例题的教学,让学生能够运用所学知识解决问题,激发学生学习的积极性.
【答案】
例1.解:直线AM是线段BC的垂直平分线.
理由如下:∵AB=AC,
∴点A在线段BC的垂直平分线上.
∵MB=MC,
∴点M在线段BC的垂直平分线上.
∴直线AM是线段BC的垂直平分线.
例2.已知:直线AB和AB外一点C.(如图)
求作:AB的垂线,使它经过点C.
作法:
(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C为圆心,CK长为半径作弧,
交AB于点D和点E.
(3)分别以点D和点E为圆心,大于DE的长为半径作弧,两弧相交于点F.
(4)作直线CF.直线CF就是所求作的垂线.
例3.解:∵ 点E在BA的垂直平分线上,
∴ AE=BE.
∵ △BCE的周长=BC+CE+BE=50,
∴ BC+CE+AE=BC+AC=50.
∵ AC=27,
∴ BC=23.
第四环节 【随堂练习 巩固新知】
1.(2019秋 蓝山县期中)下列说法:①若直线PE是线段AB的垂直平分线,则EA=EB,PA=PB;②若PA=PB,EA=EB,则直线PE垂直平分线段AB;③若PA=PB,则点P必是线段AB的垂直平分线上的点;④若EA=EB,则过点E的直线垂直平分线段AB.其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
2.(2020 和平区校级模拟)如图,在四边形ABCD中,AC⊥BD,垂足为E,且BE=DE,下列结论不一定成立的是( )
A.AB=AD B.AC=BD
C.CA平分∠BCD D.△BEC≌△DEC
3.(2019秋 大冶市期末)如图,DE是△ABC中AC边上的垂直平分线,如果BC=8cm,AB=10cm,则△EBC的周长为( )
A.16cm B.18cm C.26cm D.28cm
4.(2019秋 清江浦区期末)如图,在△ABC中,∠C=31°,∠ABC的平分线BD交AC于点D,如果DE垂直平分BC,那么∠A的度数为( )
A.31° B.62° C.87° D.93°
5.(2019秋 孟津县期末)如图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,AE=7cm,AP=4cm,则P点到直线AB的距离是 .
设计意图:本环节为基础练习,目的在于考察学生对线段的垂直平分线的性质的理解程度.
【答案】
C 2.B 3.B 4.C 5.3cm.
第五环节 【当堂检测 及时反馈】
1.(2019 梧州)如图,DE是△ABC的边AB的垂直平分线,D为垂足,DE交AC于点E,且AC=8,BC=5,则△BEC的周长是( )
A.12 B.13 C.14 D.15
2.(2019秋 博山区期中)如图所示,线段AB,AC的垂直平分线相交于点P,则PB与PC的关系是( )
A.PB>PC B.PB=PC
C.PB<PC D.PB=2PC
3.(2019 雁塔区校级模拟)如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对 B.2对 C.3对 D.4对
4.如图,△ABC中,DG垂直平分AB交AB于点D,交BC于点M,EF垂直平分AC交AC于点E,交BC于点N,且点M在点N的左侧,连接AM、AN,若BC=12cm,则△AMN的周长是( )
A.10 cm B.12 cm C.14 cm D.16 cm
5.(2020春 北镇市期中)如图,在△ABC中,BD平分∠ABC,BC的垂直平分线交BD于点E,连接CE,若∠A=60°,∠ACE=24°,则∠ABE的度数为( )
A.24° B.30° C.32° D.48°
6.(2019秋 平果县期末)如图,在△ABC中,DH是AC的垂直平分线,交BC于点P,MN是AB的垂直平分线,交BC于点O,连接AP、AQ,已知∠BAC=72°,则∠PAQ= .
7.(2019秋 息县期末)如图,BD垂直平分AG于D,CE垂直平分AF于E,若BF=1,FG=3,GC=2,则△ABC的周长为 .
8.(2019秋 三台县期末)如图,△ABC中,∠BAC=90°,AC=8cm,DE是BC边上的垂直平分线,△ABD的周长为14cm,则△ABC的面积是 cm2.
9.(2019秋 浏阳市期末)如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高,求证:AD垂直平分EF.
10.(2019秋 泰兴市期末)如图,△ABC中,∠ABC=30°,∠ACB=50°,DE、FG分别为AB、AC的垂直平分线,E、G分别为垂足.
求∠DAF的度数;
若△DAF的周长为10,求BC的长.
设计意图:通过本环节练习,锻炼学生的思维,考察学生能否灵活应用本课知识进行求解,突出本课重点.
【答案】
B 2.B 3.D 4.B 5.C
6.36°. 7.15. 8.24.
9.证明:设AD、EF的交点为K,
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴DE=DF,∠AED=∠AFD=90°,
在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF.
∴AD是线段EF的垂直平分线.
10.解:(1)∠BAC=180°-∠ABC-∠ACB
=180°-30°-50°=100°,
∵DE是AB的垂直平分线,∴DA=DB,
∴∠DAB=∠ABC=30°,
∵FG是AC的垂直平分线,∴FA=FC,
∴∠FAC=∠ACB=50°,
∴∠DAF=∠BAC-(∠DAB+∠FAC)=20°;
(2)∵△DAF的周长为10,
∴AD+DF+FC=10,
∴BC=BD+DF+FC=AD+DF+FC=10.
第六环节 【拓展延伸 能力提升】
1.(2019秋 莱西市期中)如图,四边形ABCD中,∠A=∠B=90°,AB=25cm,DA=15cm,CB=10cm.动点E从A点出发,以2cm/s的速度向B点移动,设移动的时间为x秒.
(1)当x为何值时,点E在线段CD的垂直平分线上?
(2)在(1)的条件下,判断DE与CE的位置关系,并说明理由.
2.如图,OE,OF分别是△ABC中AB,AC边的中垂线(即垂直平分线),∠OBC、∠OCB的平分线相交于点I,试判定OI与BC的位置关系,并给出证明.
设计意图:本环节的目的在于拓展学生的知识面,展现有梯度的教学理念.
【答案】
1.解:(1)当x=5时,点E在线段CD的垂直平分线上,
理由是:当x=5时,AE=2×5cm=10cm=BC,
∵AB=25cm,DA=15cm,CB=10cm,
∴BE=AD=15cm,
在△ADE和△BEC中,
∴△ADE≌△BEC(SAS),
∴DE=CE,
∴点E在线段CD的垂直平分线上,
即当x=5时,点E在线段CD的垂直平分线上;
(2)DE与CE的位置关系是DE⊥CE,
理由是:∵△ADE≌△BEC,
∴∠ADE=∠CEB,
∵∠A=90°,
∴∠ADE+∠AED=90°,
∴∠AED+∠CEB=90°,
∴∠DEC=180°-(∠AED+∠CEB)=90°,
∴DE⊥CE.
2.解:OI⊥BC.
理由:连接OA,过点I作IM⊥OB于点M,过点I作IN⊥OC于点N,过点I作IG⊥BC于点G,
∵OE,OF分别是AB,AC边的中垂线,
∴OA=OB,OA=OC,
∴OB=OC,
∵∠OBC,∠OCB的平分线相交于点I,
∴IM=IG,IN=IG,
∴IM=IN,
∴点I在∠BOC的角平分线上,
∵OB=OC,
∴OI⊥BC.
第七环节 【总结反思 知识内化】
设计意图:通过小结,使学生梳理本节课所学内容,突出重点.
第八环节 【布置作业 夯实基础】
