12.2.1 三角形全等的判定(SSS) 教案 2023--2024学年人教版八年级数学上册
文档属性
| 名称 | 12.2.1 三角形全等的判定(SSS) 教案 2023--2024学年人教版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 400.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览




文档简介
第十二章 全等三角形
·12.2三角形全等的判定·
第一课时 三角形全等的判定(SSS)
教案
班级: 课时: 课型:
学情分析
学生通过上节课的学习,了解了全等图形的概念及特征,掌握了全等图形的对应边和对应角的关系,这为探究三角形全等的条件打下了基础.另外,该阶段的学生具备了用尺规作最简单图形的能力,减小本课的探究难度.
二、教学目标
1.经历探索判定三角形全等条件(SSS)的过程,体会分类的数学方法.
2.掌握“边边边”判定两个三角形全等的方法,理解三角形的稳定性.
3.通过三角形全等的证明,培养有条理的思考和表达能力.
三、重点难点
【教学重点】
“边边边”判定两个三角形全等的方法及应用.
【教学难点】
理解证明的基本过程,初步学会综合分析法.
四、教学过程设计
第一环节 【复习旧知 引入新课】
1.什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
3.已知△ABC≌△A'B'C',试找出其中相等的边与角.
∵ △ABC≌△A'B'C',
∴ (1)AB = A'B',(2)BC = B'C',(3)CA = C'A',(4)∠A =∠A',(5)∠B =∠B',(6)∠C =∠C'.
教师提出问题:满足这六个条件,可得到什么结论?
通过PPT展示,可以得到△ABC≌△A'B'C'.
用文字叙述为三条边对应相等,三个角对应相等的两个三角形全等.(这是全等三角形的定义)
教师提出能否在上述六个条件中选择部分条件,简捷地判定两个三角形全等?
引发学生思考,同时揭示本课课题——今天我们一起来探究判定三角形全等的条件.
设计意图:以问题串的形式让学生回顾全等三角形的相关概念,通过全等三角形的性质得到三角形全等的一种判定方法,以此提出判定两个三角形全等是否还有其他的条件,引发学生思考,由易到难,循序渐进.
第二环节 【合作交流 探索新知】
探究一:如果满足六个条件中的一个,是否可以判定两个三角形全等呢?
先任意画出一个△ABC.再画出一个△A'B'C',使△ABC与△A'B'C'满足上述六个条件中的一个(一边或一角分别相等).你画出的△A'B'C'与△ABC一定全等吗?
学生经历探究发现,有一条边相等或有一个角相等的两个三角形不一定全等.
探究二:如果满足两个条件呢?并给出以下几种情况与学生探究.
1.有两个角对应相等的两个三角形.
2.有两条边对应相等的两个三角形.
3.有一个角和一条边对应相等的两个三角形.
学生独立思考,然后小组进行探究,通过画图,展示交流,最后得出,满足两个条件的另两个三角形不一定全等.
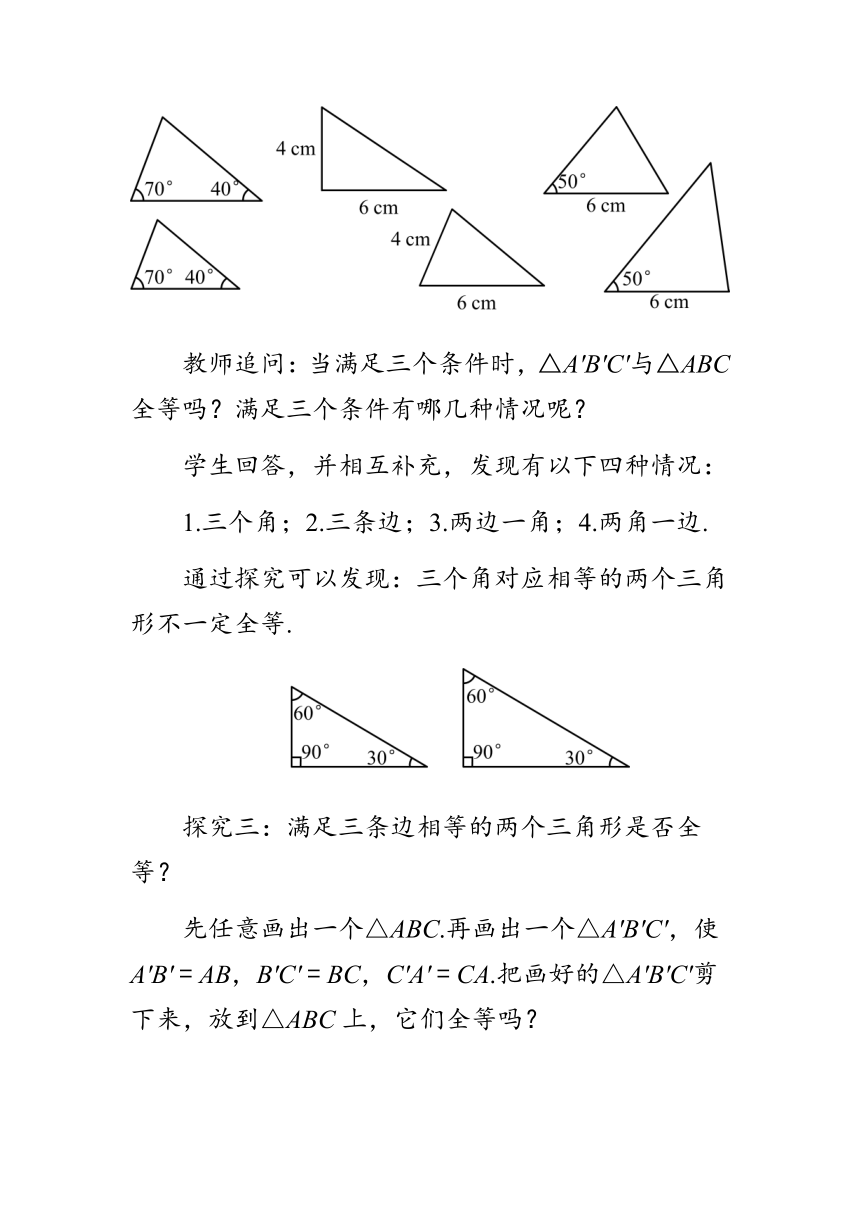
教师追问:当满足三个条件时,△A'B'C'与△ABC全等吗?满足三个条件有哪几种情况呢?
学生回答,并相互补充,发现有以下四种情况:
1.三个角;2.三条边;3.两边一角;4.两角一边.
通过探究可以发现:三个角对应相等的两个三角形不一定全等.
探究三:满足三条边相等的两个三角形是否全等?
先任意画出一个△ABC.再画出一个△A'B'C',使A'B' = AB,B'C' = BC,C'A' = CA.把画好的△A'B'C'剪下来,放到△ABC上,它们全等吗?
师生活动:师生共同用尺规作图,学生剪图、比较图.具体过程如下:(1)学生在已画出△ABC的相同的纸上分别用尺规作出线段B'C',使B'C'=BC,进而确定B'、C'的位置;(2)由于此时应同时满足A'B' = AB,C'A' = CA,所以分别以B',C'为圆心,线段AB,AC长为半径画弧,两弧相交于点A',把△A'B'C'画出来,将其剪下,放到△ABC上.
师:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
生:三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
教师展示符号语言的表达:
在△ABC和△A'B'C'中,
∴ △ABC≌△A'B'C'(SSS).
教师指出:判断两个三角形全等的推理过程,叫做证明三角形全等.
思考:我们曾做过这样的实验:将三根木条用钉子钉成一个三角形木架,这个木架的形状、大小就不变了.你能用“边边边”解释三角形具有稳定性吗?
生:三角形三条边的长度确定了,这个三角形的形状、大小也就确定了.这就是三角形具有稳定性的原因.
设计意图:本环节通过构建三角形全等条件的探索路径,以问题串的形式进行探究,由浅到深引导学生思考,让学生经历作图、剪图等过程,感悟基本事实,并用所学知识解释生活现象,进一步感受数学的应用价值.
第三环节 【应用迁移 巩固提高】
例1.在如图所示的三角形钢架中,AB = AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
例2.已知:∠AOB.
求作:∠A'O'B',使∠A'O'B' =∠AOB.
例3.(2020 云南模拟)如图,AB = DE,AC = DF,BE = CF,求证:△ABC≌△DEF.
设计意图:本环节结合新课知识对例题进行讲解,培养学生的论证推理能力,并通过解题过程,归纳证明三角形全等的步骤,锻炼学生的归纳能力.
【答案】
例1.证明:∵ D是BC的中点,
∴ BD = CD.
在△ABD和△ACD中,
∴ △ABD≌△ACD(SSS).
例2.作法:(1)以点O为圆心,以任意长为半径画弧,分别交OA,交OB于点C,D.
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
(3)以点C'为圆心,以CD长为半径画弧,与第 2 步中所画的弧相交于点D'.
(4)过点D'作射线O'B',则∠A'O'B' =∠AOB.
如图,∠A'O'B'即为所求.
例3.证明:∵ BE = CF,
∴ BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS).
第四环节 【随堂练习 巩固新知】
1.如图,△ABC中,AB = AC,EB = EC,则由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
2.△ABC和△DEF中,AB = 3,BC = 4,CA = 5,DE = 5,EF = 4,要使△ABC与△DEF全等,则DF等于( )
A.3 B.4 C.5 D.不能确定
3.(2019秋 滨海县期中)三角形具有稳定性,就是当三角形的三边长确定时,三角形的形状和大小就确定了,其理论依据是( )
A.SAS B.ASA C.AAS D.SSS
4.如图,已知在△ABC与△DCB中,AC = DB,若不增加任何字母与辅助线,要使△ABC≌△DCB(SSS).则还需要添加的一个条件是 .
5.如图,射线AB交CD于O,AC = AD,BC = BD,OC = OD,则图中全等三角形有
,共 对.
设计意图:学生利用“SSS”判定方法解答简单练习,加深对新学知识的理解,巩固好基础.
【答案】
B 2.A 3.D
4.AB=DC 5.△ACB≌△ADB,ACO≌△ADO,△BCO≌△BDO,3.
第五环节 【当堂检测 及时反馈】
1.如图,下列三角形中,与△ABC全等的是_____.
2.(2019秋 平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
3.(2019秋 江城区期末)如图,已知AC = FE,BC = DE,点A、D、B、F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD = FB B.DE = BD
C.BF = DB D.以上都不对
4.如图,已知AB = CD,BC = DA,下列结论:①∠BAC =∠DCA;②∠ACB =∠CAD;③AB∥CD.其中正确的结论有( )
A.0 个 B.1 个 C.2 个 D.3 个
5.(2019秋 黄陂区期末)在如图所示3×3的正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画( )个
A.1 B.2 C.3 D.4
6.如图,AB = ED,AC = EC,C是BD边的中点,若∠A = 36°,则∠E = .
7.如图所示,过点C作直线DE,使DE∥AB.
8.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM = ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C的射线OC便是∠AOB的平分线.为什么?
9.如图,AC、BD相交于点O,AC = BD,AB = DC,求证:∠A =∠D.
10.如图,在四边形ABCD中,AB = CD,AD = BC,AB与CD平行吗?请说明理由.
设计意图:学生运用“SSS”判定方法进行解答及推理论证,锻炼学生的推理论证和综合分析能力.
【答案】
② 2.A 3.A 4.D 5.D 6.36°
7.作法:(1)过点C作直线MN与AB相交,交点为F;
(2)在直线MN的右侧作∠FCE,使∠FCE =∠AFC;
(3)反向延长CE,则直线DE即为所求.
8.解:在△COM和△CON中,,
∴ △COM≌△CON(SSS).
∴ ∠COM = ∠CON.
∴ 射线OC是∠AOB的平分线.
9.证明:连接B、C两点,
在△ABC和△DBC中,
∴ △ABC≌△DBC(SSS).
∴ ∠A =∠D.
10.解:AB与CD平行,理由如下:
∵ AD = BC,
∴ BC = DA.
在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS).
∴ ∠BAC =∠DCA.
∴ AB∥CD.
第六环节 【拓展延伸 能力提升】
1.如图,已知AB = AC,AD = AE,BD = CE,求证:∠3 =∠1+∠2.
2.已知C是BD上一点,AC = CE,AB = CD,BC = DE,∠B = 90°.
求证:AC⊥CE.
设计意图:全等三角形的判定在几何论证中有这十分重要的地位,本环节主要考察学生的综合能力,展现有层次的教学.
【答案】
1.证明:在△ABD和△ACE中,
∴ △ABD≌△ACE(SSS).
∴ ∠2 =∠ABD,∠1 =∠BAD.
∵ ∠3 =∠ABD+∠BAD,
∴ ∠3 =∠1+∠2.
2.证明:在△ABC和△CDE中,
∴ △ABC≌△CDE(SSS).
∴ ∠B =∠D = 90°,∠A =∠ECD,∠ACB =∠E.
∵ ∠A +∠ACB = 90°,
∴ ∠ACB +∠ECD = 90°,
∴ ∠ACE = 180°-(∠ACB +∠ECD)= 90°.
∴ AC⊥CE.
第七环节 【总结反思 知识内化】
课堂小结:
1.已知三角形三条边的长度,画三角形;
2.三边分别相等的两个三角形全等(简写成“边边边”或“SSS”);
3.初步学会证明的思路,应用“边边边”证明两个三角形全等.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
·12.2三角形全等的判定·
第一课时 三角形全等的判定(SSS)
教案
班级: 课时: 课型:
学情分析
学生通过上节课的学习,了解了全等图形的概念及特征,掌握了全等图形的对应边和对应角的关系,这为探究三角形全等的条件打下了基础.另外,该阶段的学生具备了用尺规作最简单图形的能力,减小本课的探究难度.
二、教学目标
1.经历探索判定三角形全等条件(SSS)的过程,体会分类的数学方法.
2.掌握“边边边”判定两个三角形全等的方法,理解三角形的稳定性.
3.通过三角形全等的证明,培养有条理的思考和表达能力.
三、重点难点
【教学重点】
“边边边”判定两个三角形全等的方法及应用.
【教学难点】
理解证明的基本过程,初步学会综合分析法.
四、教学过程设计
第一环节 【复习旧知 引入新课】
1.什么叫全等三角形?
能够完全重合的两个三角形叫全等三角形.
2.全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
3.已知△ABC≌△A'B'C',试找出其中相等的边与角.
∵ △ABC≌△A'B'C',
∴ (1)AB = A'B',(2)BC = B'C',(3)CA = C'A',(4)∠A =∠A',(5)∠B =∠B',(6)∠C =∠C'.
教师提出问题:满足这六个条件,可得到什么结论?
通过PPT展示,可以得到△ABC≌△A'B'C'.
用文字叙述为三条边对应相等,三个角对应相等的两个三角形全等.(这是全等三角形的定义)
教师提出能否在上述六个条件中选择部分条件,简捷地判定两个三角形全等?
引发学生思考,同时揭示本课课题——今天我们一起来探究判定三角形全等的条件.
设计意图:以问题串的形式让学生回顾全等三角形的相关概念,通过全等三角形的性质得到三角形全等的一种判定方法,以此提出判定两个三角形全等是否还有其他的条件,引发学生思考,由易到难,循序渐进.
第二环节 【合作交流 探索新知】
探究一:如果满足六个条件中的一个,是否可以判定两个三角形全等呢?
先任意画出一个△ABC.再画出一个△A'B'C',使△ABC与△A'B'C'满足上述六个条件中的一个(一边或一角分别相等).你画出的△A'B'C'与△ABC一定全等吗?
学生经历探究发现,有一条边相等或有一个角相等的两个三角形不一定全等.
探究二:如果满足两个条件呢?并给出以下几种情况与学生探究.
1.有两个角对应相等的两个三角形.
2.有两条边对应相等的两个三角形.
3.有一个角和一条边对应相等的两个三角形.
学生独立思考,然后小组进行探究,通过画图,展示交流,最后得出,满足两个条件的另两个三角形不一定全等.
教师追问:当满足三个条件时,△A'B'C'与△ABC全等吗?满足三个条件有哪几种情况呢?
学生回答,并相互补充,发现有以下四种情况:
1.三个角;2.三条边;3.两边一角;4.两角一边.
通过探究可以发现:三个角对应相等的两个三角形不一定全等.
探究三:满足三条边相等的两个三角形是否全等?
先任意画出一个△ABC.再画出一个△A'B'C',使A'B' = AB,B'C' = BC,C'A' = CA.把画好的△A'B'C'剪下来,放到△ABC上,它们全等吗?
师生活动:师生共同用尺规作图,学生剪图、比较图.具体过程如下:(1)学生在已画出△ABC的相同的纸上分别用尺规作出线段B'C',使B'C'=BC,进而确定B'、C'的位置;(2)由于此时应同时满足A'B' = AB,C'A' = CA,所以分别以B',C'为圆心,线段AB,AC长为半径画弧,两弧相交于点A',把△A'B'C'画出来,将其剪下,放到△ABC上.
师:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
生:三边分别相等的两个三角形全等(简写成“边边边”或“SSS”).
教师展示符号语言的表达:
在△ABC和△A'B'C'中,
∴ △ABC≌△A'B'C'(SSS).
教师指出:判断两个三角形全等的推理过程,叫做证明三角形全等.
思考:我们曾做过这样的实验:将三根木条用钉子钉成一个三角形木架,这个木架的形状、大小就不变了.你能用“边边边”解释三角形具有稳定性吗?
生:三角形三条边的长度确定了,这个三角形的形状、大小也就确定了.这就是三角形具有稳定性的原因.
设计意图:本环节通过构建三角形全等条件的探索路径,以问题串的形式进行探究,由浅到深引导学生思考,让学生经历作图、剪图等过程,感悟基本事实,并用所学知识解释生活现象,进一步感受数学的应用价值.
第三环节 【应用迁移 巩固提高】
例1.在如图所示的三角形钢架中,AB = AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
例2.已知:∠AOB.
求作:∠A'O'B',使∠A'O'B' =∠AOB.
例3.(2020 云南模拟)如图,AB = DE,AC = DF,BE = CF,求证:△ABC≌△DEF.
设计意图:本环节结合新课知识对例题进行讲解,培养学生的论证推理能力,并通过解题过程,归纳证明三角形全等的步骤,锻炼学生的归纳能力.
【答案】
例1.证明:∵ D是BC的中点,
∴ BD = CD.
在△ABD和△ACD中,
∴ △ABD≌△ACD(SSS).
例2.作法:(1)以点O为圆心,以任意长为半径画弧,分别交OA,交OB于点C,D.
(2)画一条射线O'A',以点O'为圆心,OC长为半径画弧,交O'A'于点C';
(3)以点C'为圆心,以CD长为半径画弧,与第 2 步中所画的弧相交于点D'.
(4)过点D'作射线O'B',则∠A'O'B' =∠AOB.
如图,∠A'O'B'即为所求.
例3.证明:∵ BE = CF,
∴ BE+EC = CF+EC,即BC = EF,
在△ABC和△DEF中,
∴ △ABC≌△DEF(SSS).
第四环节 【随堂练习 巩固新知】
1.如图,△ABC中,AB = AC,EB = EC,则由“SSS”可以判定( )
A.△ABD≌△ACD B.△ABE≌△ACE
C.△BDE≌△CDE D.以上答案都不对
2.△ABC和△DEF中,AB = 3,BC = 4,CA = 5,DE = 5,EF = 4,要使△ABC与△DEF全等,则DF等于( )
A.3 B.4 C.5 D.不能确定
3.(2019秋 滨海县期中)三角形具有稳定性,就是当三角形的三边长确定时,三角形的形状和大小就确定了,其理论依据是( )
A.SAS B.ASA C.AAS D.SSS
4.如图,已知在△ABC与△DCB中,AC = DB,若不增加任何字母与辅助线,要使△ABC≌△DCB(SSS).则还需要添加的一个条件是 .
5.如图,射线AB交CD于O,AC = AD,BC = BD,OC = OD,则图中全等三角形有
,共 对.
设计意图:学生利用“SSS”判定方法解答简单练习,加深对新学知识的理解,巩固好基础.
【答案】
B 2.A 3.D
4.AB=DC 5.△ACB≌△ADB,ACO≌△ADO,△BCO≌△BDO,3.
第五环节 【当堂检测 及时反馈】
1.如图,下列三角形中,与△ABC全等的是_____.
2.(2019秋 平山县期末)我国的纸伞工艺十分巧妙.如图,伞不论张开还是缩拢,伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC,从而保证伞圈D能沿着伞柄滑动.为了证明这个结论,我们的依据是( )
A.SSS B.SAS C.AAS D.ASA
3.(2019秋 江城区期末)如图,已知AC = FE,BC = DE,点A、D、B、F在一条直线上,要利用“SSS”证明△ABC≌△FDE,还可以添加的一个条件是( )
A.AD = FB B.DE = BD
C.BF = DB D.以上都不对
4.如图,已知AB = CD,BC = DA,下列结论:①∠BAC =∠DCA;②∠ACB =∠CAD;③AB∥CD.其中正确的结论有( )
A.0 个 B.1 个 C.2 个 D.3 个
5.(2019秋 黄陂区期末)在如图所示3×3的正方形网格中,△ABC的顶点都在小正方形的顶点上,像△ABC这样顶点均在格点上的三角形叫格点三角形,在图中画与△ABC有一条公共边且全等的格点三角形,这样的格点三角形最多可以画( )个
A.1 B.2 C.3 D.4
6.如图,AB = ED,AC = EC,C是BD边的中点,若∠A = 36°,则∠E = .
7.如图所示,过点C作直线DE,使DE∥AB.
8.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB是一个任意角,在边OA,OB上分别取OM = ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合.过角尺顶点C的射线OC便是∠AOB的平分线.为什么?
9.如图,AC、BD相交于点O,AC = BD,AB = DC,求证:∠A =∠D.
10.如图,在四边形ABCD中,AB = CD,AD = BC,AB与CD平行吗?请说明理由.
设计意图:学生运用“SSS”判定方法进行解答及推理论证,锻炼学生的推理论证和综合分析能力.
【答案】
② 2.A 3.A 4.D 5.D 6.36°
7.作法:(1)过点C作直线MN与AB相交,交点为F;
(2)在直线MN的右侧作∠FCE,使∠FCE =∠AFC;
(3)反向延长CE,则直线DE即为所求.
8.解:在△COM和△CON中,,
∴ △COM≌△CON(SSS).
∴ ∠COM = ∠CON.
∴ 射线OC是∠AOB的平分线.
9.证明:连接B、C两点,
在△ABC和△DBC中,
∴ △ABC≌△DBC(SSS).
∴ ∠A =∠D.
10.解:AB与CD平行,理由如下:
∵ AD = BC,
∴ BC = DA.
在△ABC和△CDA中,
∴ △ABC≌△CDA(SSS).
∴ ∠BAC =∠DCA.
∴ AB∥CD.
第六环节 【拓展延伸 能力提升】
1.如图,已知AB = AC,AD = AE,BD = CE,求证:∠3 =∠1+∠2.
2.已知C是BD上一点,AC = CE,AB = CD,BC = DE,∠B = 90°.
求证:AC⊥CE.
设计意图:全等三角形的判定在几何论证中有这十分重要的地位,本环节主要考察学生的综合能力,展现有层次的教学.
【答案】
1.证明:在△ABD和△ACE中,
∴ △ABD≌△ACE(SSS).
∴ ∠2 =∠ABD,∠1 =∠BAD.
∵ ∠3 =∠ABD+∠BAD,
∴ ∠3 =∠1+∠2.
2.证明:在△ABC和△CDE中,
∴ △ABC≌△CDE(SSS).
∴ ∠B =∠D = 90°,∠A =∠ECD,∠ACB =∠E.
∵ ∠A +∠ACB = 90°,
∴ ∠ACB +∠ECD = 90°,
∴ ∠ACE = 180°-(∠ACB +∠ECD)= 90°.
∴ AC⊥CE.
第七环节 【总结反思 知识内化】
课堂小结:
1.已知三角形三条边的长度,画三角形;
2.三边分别相等的两个三角形全等(简写成“边边边”或“SSS”);
3.初步学会证明的思路,应用“边边边”证明两个三角形全等.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
