2023-2024学年第一学期甘肃省武威市凉州区清水镇九年制学校九年级数学《二次函数》寒假复习作业(含答案)
文档属性
| 名称 | 2023-2024学年第一学期甘肃省武威市凉州区清水镇九年制学校九年级数学《二次函数》寒假复习作业(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 75.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 00:00:00 | ||
图片预览



文档简介
2023-2024学年第一学期甘肃省武威市凉州区清水镇九年制学校
九年级数学《二次函数》寒假复习作业
二次函数综合训练(共20题;共120分)
1.(4分)已知二次函数的表达式为y=
x2+x+2.
(1)(2分)求该二次函数图象的开口方向、对称轴和顶点坐标;
(2)(2分)当x小于多少时,y随x的增大而增大?
2.(4分)已知函数 是二次函数.
(1)(2分)求m的值;
(2)(2分)求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.
3.(4分)已知关于x的二次函数 ,其图像经过点(1,8).
(1)(2分)求k的值.
(2)(2分)求出函数图象的顶点坐标.
4.(4分)如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
(1)(2分)求梯形的面积y与高x的表达式;
(2)(2分)求x的取值范围.
5.(4分)已知二次函数 .
(1)(2分)求抛物线开口方向及对称轴.
(2)(2分)写出抛物线与y轴的交点坐标.
6.(4分)在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.
(1)(2分)直接写出抛物线的顶点坐标;
(2)(2分)求抛物线的解析式.
7.(6分)如图,矩形ABCD的长AD=5 cm,宽AB=3 cm,长和宽都增加x cm,那么面积增加y cm2.
(1)(3分)写出y与x的函数关系式;
(2)(3分)当增加的面积y=20 cm2时,求相应的x是多少?
8.(6分)如图,二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,顶点为D.
(1)(3分)求此二次函数的解析式.
(2)(3分)求点D的坐标及△ABD的面积.
9.(6分)二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=﹣1.
(1)(3分)求函数解析式;
(2)(3分)若图象与x轴交于A、B(A在B左)与y轴交于C,顶点D,求四边形ABCD的面积.
10.(6分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,图像交x轴于A、B(-1,0)两点,交y轴于点C(0,3),根据图像解答下列问题:
(1)(3分)直接写出方程ax2+bx+c=0的两个根;
(2)(3分)直接写出不等式ax2+bx+c<3的解集.
11.(6分)如图,已知二次函数y=ax +bx+c的图象与x轴交于点A、B,与y轴交于点C.
(1)(3分)写出A、B、C三点的坐标;
(2)(3分)求出二次函数的解析式.
12.(10分)商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场每天可多售出2件,设每件商品降低x元据此规律,请回答:
(1)(4分)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(2)(3分)在上述条件不变,销售正常的情况下,设商场日盈利y元,求y与x的函数关系式;
(3)(3分)在(2)的条件下,每件商品降价多少元时,商场日盈利最高?
13.(6分)已知抛物线的顶点坐标为(-1,2),与y轴交于点(0, )
(1)(3分)求二次函数的解析式;
(2)(3分)判断点P(2,- )是否落在抛物线上,请说明理由.
14.(6分)如图,用20m的篱笆围成一个矩形的花圃.设连墙的一边为x(m),矩形的面积为y(m2).
(1)(3分)写出y关于x的函数解析式;
(2)(3分)当x=3时,矩形的面积为多少?
15.(6分)某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)(3分)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)(3分)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
16.(6分)已知二次函数y=ax2的图象经过A(2,﹣4)
(1)(3分)求这个二次函数的解析式;
(2)(3分)请写出这个二次函数图象的顶点坐标、对称轴和开口方向.
17.(6分)已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)(3分)求这个二次函数的解析式;
(2)(3分)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
18.(6分)若二次函数 的x与y的部分对应值如下表:
x -1 0 1 2 3 4
y 0 3 4 3 0 -5
(1)(3分)求这个二次函数的表达式;
(2)(3分)当x=﹣2时,y的值.
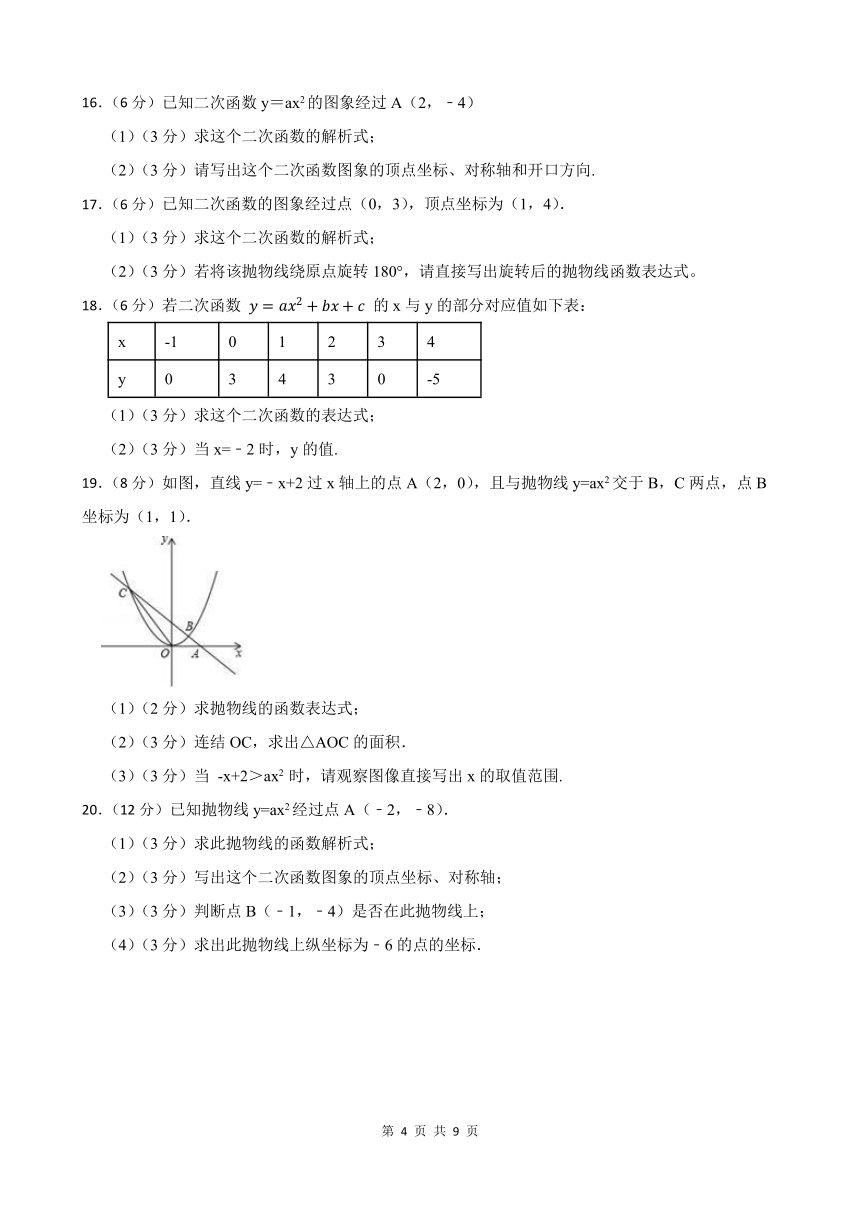
19.(8分)如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
(1)(2分)求抛物线的函数表达式;
(2)(3分)连结OC,求出△AOC的面积.
(3)(3分)当 -x+2>ax2 时,请观察图像直接写出x的取值范围.
20.(12分)已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)(3分)求此抛物线的函数解析式;
(2)(3分)写出这个二次函数图象的顶点坐标、对称轴;
(3)(3分)判断点B(﹣1,﹣4)是否在此抛物线上;
(4)(3分)求出此抛物线上纵坐标为﹣6的点的坐标.
答案
1.(1)解:y= x2+x+2 = (x2-4x+4-4)+2= (x-2)2+3,
∴该二次函数图象的开口向下,对称轴为直线x=2,顶点坐标为(2,3).
(2)解:∵二次函数图象开口向下,
∴在对称轴的左侧y随x的增大而增大,
∴当x<2时,y随x的增大而增大.
2.(1)∵
∴
∵
∴m≠3
∴
(2)将m=-3代入解析式中,得二次函数的解析式为
∵a=-6<0
∴开口方向向下
∴对称轴是直线 ,顶点坐标是(-2,-5).
3.(1)解:把(1,8)代入二次函数 得:
解得:k=5
(2)解:把k=5代入二次函数得:
化简
∴二次函数得顶点坐标为(-2,-1)
4.(1)解:如图,连接DE,过点A作AE⊥BC于E,则四边形ADCE为矩形,DC=AE=x,∠DAE=∠AEB=90°,
则∠BAE=∠BAD﹣∠EAD=45°,
在直角△CDE中,
又∵∠AEB=90°,
∴∠B=45°,
∴DC=AE=BE=x,
∴AD=CE=30﹣2x,
∴梯形ABCD面积y= (AD+BC) CD= (30﹣2x+30﹣x) x=﹣ x2+30x
(2)解:∵ ,
∴0<x<15
5.(1)解:∵ ,
∴抛物线开口向上,
∵ = ,
∴对称轴是直线 ;
(2)解:∵ ,
∴ ,
∴与y轴交点坐标是 .
6.(1)解:(2,﹣2)
(2)解:∵抛物线的顶点坐标为(2,﹣2);∴抛物线的解析式为:y=(x﹣2)2﹣2,即抛物线的解析式为:y=x2﹣4x+2.
7.(1)解:由题意可得(5+x)(3+x)-3×5=y,化简得:y=x2+8x
(2)解:把y=20代入解析式y=x2+8x中,得x2+8x-20=0,
解得x1=2,x2=-10(舍去).
∴当增加的面积为20 cm2时,相应x为2 cm.
8.(1)解:∵二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴ ,
解得: ,
∴二次函数的解析式为 ;
(2)解:由(1),得: ,
∴点 ,
∵A(﹣1,0),B(3,0),
∴ ,
∴ .
9.(1)解:∵对称轴是x=-1,所以与x轴的另一个交点为(-3,0)
所以设函数的解析式为y=a(x-1)(x+3),把(0,3)代入得a=-1
所以函数的解析式为y=-(x-1)(x+3)或y= x2-2x+3
(2)解:根据题意得:C(0,3) D(-1,4),连接OD, ∴S=
9。
10.(1)解:B(-1,0),对称轴为直线x=1,则点A(3,0),故ax2+bx+c=0的两个根为x1=3、x2=-1
(2)解:点C(0,3),则点C关于对称轴的对称点为:(2,3),则不等式ax2+bx+c<3的解集
为x<0或x>2
11.(1)A、B、C三点的坐标为A(-1,0),B(4,0),C(0,-3
(2)解:把A(-1,0),B(4,0),C(0,-3)代入y=ax2+bx+c可得
,
解得
∴y=
12.(1)2x;(50-x)
(2)解:根据题意得:
(3)解:,
当时,y有最大值,
答:每件商品降价17.5元时,商场日盈利最高.
13.(1)解:∵抛物线的顶点坐标为(-1,2),
∴设抛物线的解析式为:y=a(x+1)2+2,
将(0, )代入得,a=- ,
∴抛物线的解析式为y=- (x+1)2+2;
(2)解:将P的横坐标x=2代入抛物线,则y=- ,
所以P点落在抛物线上.
14.(1)解:设连墙的一边为x(m),矩形的面积为y(m2),
则另一边长为:(20﹣2x)m,
∴y关于x的函数解析式为:y=x(20﹣2x)=﹣2x2+20x
(2)解:当x=3时,矩形的面积为:y=﹣2×32+20×3=42(cm2)
15.(1)解:设每盆花卉应降价x元,
根据题意可得:(40-x)(20+2x)=1200,
解得:x1=10,x2=20,
∵为了增加盈利并尽快减少库存,
∴x=20,
答:若花圃平均每天要盈利1200元,每盆花卉应降价20元
(2)解:设每盆花卉降低x元,花圃每天盈利y元,
则 y=(40-x)(20+2x) =-2x2+60x+800 =-2(x-15)2+1250,
由 ,
解得:0≤x<40 ,
故当x=15时,y最大=1250,
答:每盆花卉降低15元时,花圃每天盈利最多为1250元
16.(1)解:∵二次函数y=ax2的图象经过A(2,﹣4), ∴﹣4=4a,
解得a=﹣1,
∴二次函数的解析式为y=﹣x2
(2)解:∵二次函数的解析式为 y=﹣x2,
∴这个二次函数图象的顶点坐标为(0,0),对称轴为y轴,开口方向向下
17.(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
18.(1)解:把(﹣1,0)、(0,3)、(1,4)代入 ,得
,解得: ,
∴这个二次函数的解析式是 ;
(2)解:把x=﹣2代入 ,得 .
19.(1)解:∵点B在抛物线上,
∴1=a×1,
∴a=1,
∴ y=x2 .
(2)由题意得:-x+2=x2
得 -2
∴C(-2,4)
∴
(3)-2<x<1
20.(1)解:∵抛物线y=ax2经过点A(﹣2,﹣8),
∴a (﹣2)2=﹣8,
∴a=﹣2,
∴此抛物线对应的函数解析式为y=﹣2x2
(2)解:由题可得,抛物线的顶点坐标为(0,0),对称轴为y轴
(3)解:把x=﹣1代入得,y=﹣2×(﹣1)2=﹣2≠﹣4,
∴点B(﹣1,﹣4)不在此抛物线上
(4)解:把y=﹣6代入y=﹣2x2得,﹣6=﹣2x2,
解得x=± ,
∴抛物线上纵坐标为﹣6的点的坐标为( ,﹣6)或(﹣ ,﹣6)
九年级数学《二次函数》寒假复习作业
二次函数综合训练(共20题;共120分)
1.(4分)已知二次函数的表达式为y=
x2+x+2.
(1)(2分)求该二次函数图象的开口方向、对称轴和顶点坐标;
(2)(2分)当x小于多少时,y随x的增大而增大?
2.(4分)已知函数 是二次函数.
(1)(2分)求m的值;
(2)(2分)求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.
3.(4分)已知关于x的二次函数 ,其图像经过点(1,8).
(1)(2分)求k的值.
(2)(2分)求出函数图象的顶点坐标.
4.(4分)如图,校园要建苗圃,其形状如直角梯形,有两边借用夹角为135°的两面墙,另外两边是总长为30m的铁栅栏.
(1)(2分)求梯形的面积y与高x的表达式;
(2)(2分)求x的取值范围.
5.(4分)已知二次函数 .
(1)(2分)求抛物线开口方向及对称轴.
(2)(2分)写出抛物线与y轴的交点坐标.
6.(4分)在平面直角坐标系中,已知抛物线y=x2+bx+c的对称轴为x=2,且其顶点在直线y=﹣2x+2上.
(1)(2分)直接写出抛物线的顶点坐标;
(2)(2分)求抛物线的解析式.
7.(6分)如图,矩形ABCD的长AD=5 cm,宽AB=3 cm,长和宽都增加x cm,那么面积增加y cm2.
(1)(3分)写出y与x的函数关系式;
(2)(3分)当增加的面积y=20 cm2时,求相应的x是多少?
8.(6分)如图,二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,顶点为D.
(1)(3分)求此二次函数的解析式.
(2)(3分)求点D的坐标及△ABD的面积.
9.(6分)二次函数y=ax2+bx+c的图象过点(1,0)(0,3),对称轴x=﹣1.
(1)(3分)求函数解析式;
(2)(3分)若图象与x轴交于A、B(A在B左)与y轴交于C,顶点D,求四边形ABCD的面积.
10.(6分)二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=1,图像交x轴于A、B(-1,0)两点,交y轴于点C(0,3),根据图像解答下列问题:
(1)(3分)直接写出方程ax2+bx+c=0的两个根;
(2)(3分)直接写出不等式ax2+bx+c<3的解集.
11.(6分)如图,已知二次函数y=ax +bx+c的图象与x轴交于点A、B,与y轴交于点C.
(1)(3分)写出A、B、C三点的坐标;
(2)(3分)求出二次函数的解析式.
12.(10分)商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场每天可多售出2件,设每件商品降低x元据此规律,请回答:
(1)(4分)商场日销售量增加 件,每件商品盈利 元(用含x的代数式表示);
(2)(3分)在上述条件不变,销售正常的情况下,设商场日盈利y元,求y与x的函数关系式;
(3)(3分)在(2)的条件下,每件商品降价多少元时,商场日盈利最高?
13.(6分)已知抛物线的顶点坐标为(-1,2),与y轴交于点(0, )
(1)(3分)求二次函数的解析式;
(2)(3分)判断点P(2,- )是否落在抛物线上,请说明理由.
14.(6分)如图,用20m的篱笆围成一个矩形的花圃.设连墙的一边为x(m),矩形的面积为y(m2).
(1)(3分)写出y关于x的函数解析式;
(2)(3分)当x=3时,矩形的面积为多少?
15.(6分)某花圃销售一批名贵花卉,平均每天可售出20盆,每盆盈利40元,为了增加盈利并尽快减少库存,花圃决定采取适当的降价措施,经调查发现,如果每盆花卉每降1元,花圃平均每天可多售出2盆.
(1)(3分)若花圃平均每天要盈利1200元,每盆花卉应降价多少元?
(2)(3分)每盆花卉降低多少元时,花圃平均每天盈利最多,是多少?
16.(6分)已知二次函数y=ax2的图象经过A(2,﹣4)
(1)(3分)求这个二次函数的解析式;
(2)(3分)请写出这个二次函数图象的顶点坐标、对称轴和开口方向.
17.(6分)已知二次函数的图象经过点(0,3),顶点坐标为(1,4).
(1)(3分)求这个二次函数的解析式;
(2)(3分)若将该抛物线绕原点旋转180°,请直接写出旋转后的抛物线函数表达式。
18.(6分)若二次函数 的x与y的部分对应值如下表:
x -1 0 1 2 3 4
y 0 3 4 3 0 -5
(1)(3分)求这个二次函数的表达式;
(2)(3分)当x=﹣2时,y的值.
19.(8分)如图,直线y=﹣x+2过x轴上的点A(2,0),且与抛物线y=ax2交于B,C两点,点B坐标为(1,1).
(1)(2分)求抛物线的函数表达式;
(2)(3分)连结OC,求出△AOC的面积.
(3)(3分)当 -x+2>ax2 时,请观察图像直接写出x的取值范围.
20.(12分)已知抛物线y=ax2经过点A(﹣2,﹣8).
(1)(3分)求此抛物线的函数解析式;
(2)(3分)写出这个二次函数图象的顶点坐标、对称轴;
(3)(3分)判断点B(﹣1,﹣4)是否在此抛物线上;
(4)(3分)求出此抛物线上纵坐标为﹣6的点的坐标.
答案
1.(1)解:y= x2+x+2 = (x2-4x+4-4)+2= (x-2)2+3,
∴该二次函数图象的开口向下,对称轴为直线x=2,顶点坐标为(2,3).
(2)解:∵二次函数图象开口向下,
∴在对称轴的左侧y随x的增大而增大,
∴当x<2时,y随x的增大而增大.
2.(1)∵
∴
∵
∴m≠3
∴
(2)将m=-3代入解析式中,得二次函数的解析式为
∵a=-6<0
∴开口方向向下
∴对称轴是直线 ,顶点坐标是(-2,-5).
3.(1)解:把(1,8)代入二次函数 得:
解得:k=5
(2)解:把k=5代入二次函数得:
化简
∴二次函数得顶点坐标为(-2,-1)
4.(1)解:如图,连接DE,过点A作AE⊥BC于E,则四边形ADCE为矩形,DC=AE=x,∠DAE=∠AEB=90°,
则∠BAE=∠BAD﹣∠EAD=45°,
在直角△CDE中,
又∵∠AEB=90°,
∴∠B=45°,
∴DC=AE=BE=x,
∴AD=CE=30﹣2x,
∴梯形ABCD面积y= (AD+BC) CD= (30﹣2x+30﹣x) x=﹣ x2+30x
(2)解:∵ ,
∴0<x<15
5.(1)解:∵ ,
∴抛物线开口向上,
∵ = ,
∴对称轴是直线 ;
(2)解:∵ ,
∴ ,
∴与y轴交点坐标是 .
6.(1)解:(2,﹣2)
(2)解:∵抛物线的顶点坐标为(2,﹣2);∴抛物线的解析式为:y=(x﹣2)2﹣2,即抛物线的解析式为:y=x2﹣4x+2.
7.(1)解:由题意可得(5+x)(3+x)-3×5=y,化简得:y=x2+8x
(2)解:把y=20代入解析式y=x2+8x中,得x2+8x-20=0,
解得x1=2,x2=-10(舍去).
∴当增加的面积为20 cm2时,相应x为2 cm.
8.(1)解:∵二次函数y=x2+bx+c的图象与x轴交于A(﹣1,0),B(3,0)两点,
∴ ,
解得: ,
∴二次函数的解析式为 ;
(2)解:由(1),得: ,
∴点 ,
∵A(﹣1,0),B(3,0),
∴ ,
∴ .
9.(1)解:∵对称轴是x=-1,所以与x轴的另一个交点为(-3,0)
所以设函数的解析式为y=a(x-1)(x+3),把(0,3)代入得a=-1
所以函数的解析式为y=-(x-1)(x+3)或y= x2-2x+3
(2)解:根据题意得:C(0,3) D(-1,4),连接OD, ∴S=
9。
10.(1)解:B(-1,0),对称轴为直线x=1,则点A(3,0),故ax2+bx+c=0的两个根为x1=3、x2=-1
(2)解:点C(0,3),则点C关于对称轴的对称点为:(2,3),则不等式ax2+bx+c<3的解集
为x<0或x>2
11.(1)A、B、C三点的坐标为A(-1,0),B(4,0),C(0,-3
(2)解:把A(-1,0),B(4,0),C(0,-3)代入y=ax2+bx+c可得
,
解得
∴y=
12.(1)2x;(50-x)
(2)解:根据题意得:
(3)解:,
当时,y有最大值,
答:每件商品降价17.5元时,商场日盈利最高.
13.(1)解:∵抛物线的顶点坐标为(-1,2),
∴设抛物线的解析式为:y=a(x+1)2+2,
将(0, )代入得,a=- ,
∴抛物线的解析式为y=- (x+1)2+2;
(2)解:将P的横坐标x=2代入抛物线,则y=- ,
所以P点落在抛物线上.
14.(1)解:设连墙的一边为x(m),矩形的面积为y(m2),
则另一边长为:(20﹣2x)m,
∴y关于x的函数解析式为:y=x(20﹣2x)=﹣2x2+20x
(2)解:当x=3时,矩形的面积为:y=﹣2×32+20×3=42(cm2)
15.(1)解:设每盆花卉应降价x元,
根据题意可得:(40-x)(20+2x)=1200,
解得:x1=10,x2=20,
∵为了增加盈利并尽快减少库存,
∴x=20,
答:若花圃平均每天要盈利1200元,每盆花卉应降价20元
(2)解:设每盆花卉降低x元,花圃每天盈利y元,
则 y=(40-x)(20+2x) =-2x2+60x+800 =-2(x-15)2+1250,
由 ,
解得:0≤x<40 ,
故当x=15时,y最大=1250,
答:每盆花卉降低15元时,花圃每天盈利最多为1250元
16.(1)解:∵二次函数y=ax2的图象经过A(2,﹣4), ∴﹣4=4a,
解得a=﹣1,
∴二次函数的解析式为y=﹣x2
(2)解:∵二次函数的解析式为 y=﹣x2,
∴这个二次函数图象的顶点坐标为(0,0),对称轴为y轴,开口方向向下
17.(1)解:设二次函数解析式为y=a(x﹣1)2+4,把点(0,3)代入得a+4=3,
解得:a=﹣1,∴这个二次函数解析式为y=﹣(x﹣1)2+4.
(2)解:y=(x+1)2-4
18.(1)解:把(﹣1,0)、(0,3)、(1,4)代入 ,得
,解得: ,
∴这个二次函数的解析式是 ;
(2)解:把x=﹣2代入 ,得 .
19.(1)解:∵点B在抛物线上,
∴1=a×1,
∴a=1,
∴ y=x2 .
(2)由题意得:-x+2=x2
得 -2
∴C(-2,4)
∴
(3)-2<x<1
20.(1)解:∵抛物线y=ax2经过点A(﹣2,﹣8),
∴a (﹣2)2=﹣8,
∴a=﹣2,
∴此抛物线对应的函数解析式为y=﹣2x2
(2)解:由题可得,抛物线的顶点坐标为(0,0),对称轴为y轴
(3)解:把x=﹣1代入得,y=﹣2×(﹣1)2=﹣2≠﹣4,
∴点B(﹣1,﹣4)不在此抛物线上
(4)解:把y=﹣6代入y=﹣2x2得,﹣6=﹣2x2,
解得x=± ,
∴抛物线上纵坐标为﹣6的点的坐标为( ,﹣6)或(﹣ ,﹣6)
同课章节目录
