11.1.1三角形的边(学案) 人教版数学八年级上册
文档属性
| 名称 | 11.1.1三角形的边(学案) 人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 20:44:56 | ||
图片预览




文档简介
第十一章 三角形
·11.1与三角形有关的线段·
第一课时 三角形的边
学案
班级: 课时: 成绩:
学习目标
1.通过具体实例,进一步认识三角形的概念及其基本要素;
2.理解三角形的对边与对角的关系,掌握其三边之间的关系;
3.能将三角形按边分类.
知识构建
【自主学习】
请找出下列图片中的三角形,并将其画出.
【合作探究】
1.由 的三条线段 所组成的图形,叫做三角形.
2.判断下列图形是否为三角形.
3.组成三角形的 叫做三角形的边.
4.三角形相邻两边组成的角叫做三角形的 .简称 .
5.在△ABC中,
(1)AB边所对的角是: ,∠C所对的边是: ;
(2)BC边所对的角是: ,∠A所对的边是: ;
(3)AC边所对的角是: ,∠B所对的边是: .
6.三角形按角分类可分为 .
7.三角形如果按边进行分类,该如何分类?请在以下圆形中进行划分.
三角形
8.在A点的小狗,为了尽快吃到B点的香肠,它选择A→B路线,而不选择A→C→B路线,这体现了 的数学原理.
9.三角形两边的和 第三边,三角形两边的差 第三边.
层级练习
【应用迁移 巩固提高】
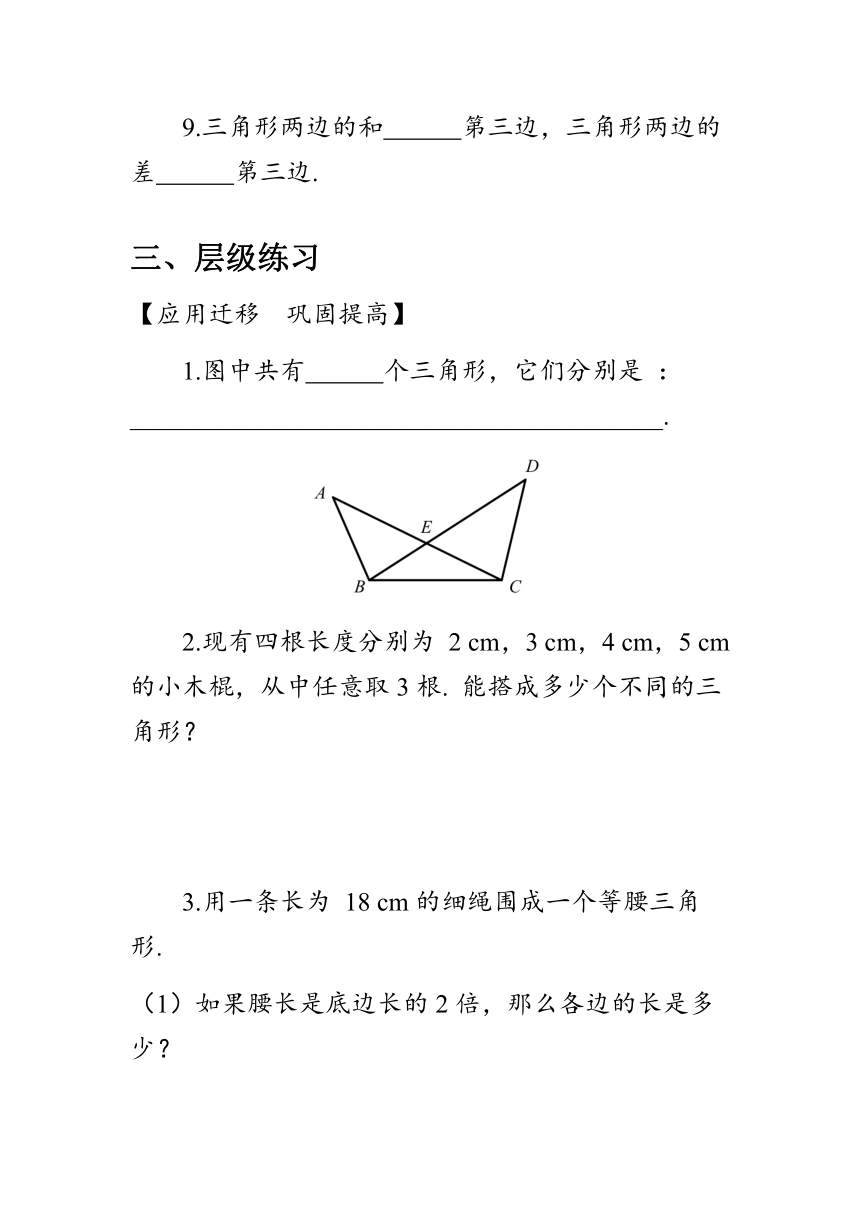
1.图中共有 个三角形,它们分别是 :_________________________________________.
2.现有四根长度分别为 2 cm,3 cm,4 cm,5 cm 的小木棍,从中任意取3根. 能搭成多少个不同的三角形?
3.用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
【随堂练习 巩固新知】
1.如图所示,图中有 个三角形;其中以AB为边的三角形为 ,含∠OCB的三角形为 ;在△BOC中,OC的对角是 ,∠OCB的对边是 .
2.(2020春 浦东新区期末)设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
3. 下列各组线段能组成一个三角形的是( )
A.3 cm,3 cm,6 cm B.2 cm,3 cm,6 cm
C.5 cm,8 cm,12 cm D.4 cm,7 cm,11 cm
4.图中有几个三角形?用符号表示这些三角形.
5.一个三角形两边分别为3和7,第三边为偶数,第三边长为__________.
【当堂检测 及时反馈】
1.(2020 浙江自主招生)如图,称有一条公共边的两个三角形为一对共边三角形,则图中的共边三角形有( )对
A.8 B.16 C.24 D.32
2.(2019 浦东新区期末)若△ABC三条边的长度分别为m,n,p,且|m-n|+(n-p)2 = 0,则这个三角形为( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
3.(2020春 沙坪坝区校级月考)下列各线段中,能与长为4,6的两线段组成三角形的是( )
A.2 B.8 C.10 D.12
4.(2019秋 江城区期末)若三角形的两边长分别为3和5,则其周长c的取值范围是( )
A.6<c<15 B.6<c<16
C.11<c<13 D.10<c<16
5. (2019春 无锡期中)如图,用四条线段首尾相接连成一个框架,其中AB = 12、BC = 14、CD = 18、DA = 24,则A、B、C、D任意两点之间的最长距离为 .
6.(2019秋 曾都区期末)我们定义三边长均为整数的三角形叫做整三角形.已知△ABC是整三角形,其周长为偶数,若AC-BC = 3.则边长AB的最小值是 .
7.(1)若三角形三条边的长分别是7,10,x,求x的范围.
(2)若三边分别为2,x-1,3,求x 的范围.
(3)若三角形两边长为7和10,求最长边x的范围.
8.一个等腰三角形的周长为18,若腰长的3倍比底边的2倍多6,求各边长.
9.(2019 嘉祥镇期中)已知a,b,c是△ABC的三边长,且b、c满足(b-5)+= 0,a为方程|a-3|= 2的解,求△ABC的周长,并判断△ABC的形状.
10.(2019秋 宜昌期中)已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)在(1)的条件下,若a=10,b=8,c=6,求这个式子.
【拓展延伸 能力提升】
1.已知:如图,P是△ABC内一点.请想一个办法说明AB+AC>PB+PC.
2.小明和小红在一本数学资料书上看到有这样一道竞赛题:“已知△ABC的三边长分别为a,b,c,且|b+c-2a|+(b+c-5)2= 0,求b的取值范围”.
(1)小明说:“b的取值范围,我看不出如何求,但我能求出a的长度.”你知道小明是如何计算的吗?帮他写出求解的过程.
(2)小红说:“我也看不出如何求b的范围,但我能用含b的代数式表示c”.帮小红写出过程.
(3)小明和小红一起去问数学老师,老师说:“根据你们二人的求解,利用书上三角形的三边满足的关系,即可求出答案.”你知道答案吗?请写出过程.
四、参考答案
【自主学习】
1.略.
【合作探究】
1.不在同一条直线上;首尾顺次相接.
2.是;否;否.
3.三条线段.
4.内角;三角形的角.
5.∠C;AB;∠A;BC;∠B;AC.
6.直角三角形、锐角三角形、钝角三角形.
7.
8.两点之间线段最短.
9.大于;小于.
【层级练习】
【应用迁移 巩固提高】
1.5;△ABE,△CDE,△BCE,△ABC,△BCD.
2.可以组成3个不同的三角形.分别是2 cm,3 cm,4 cm ;2 cm,4 cm,5 cm ;3 cm,4 cm,5 cm .
3.(1)三边长分别为 3.6 cm,7.2 cm,7.2 cm.
(2)因为长是 4 cm 的边可能是腰,也可能是底边,所以需要分情况讨论.
如果 4 cm 长的边为底边,腰长为7 cm,
如果 4 cm 长的边为腰,底边为10 cm,不符合三角形两边的和大于第三边.
由上讨论可知,可以围成底边是 4 cm 的等腰三角形.
【随堂练习 巩固新知】
1.8;△ABO、△ABC、△ABD;△BOC、△ABC;∠OBC;OB.
2.C 3.C
4.5个,分别是:△ ABD、△DPC、△CPB、△BCD、△ABC.
5.6或8.
【当堂检测 及时反馈】
1.D 2.B 3.B 4.D 5.32 6.5
7.(1)根据三角形三边关系,得10-7<x<10+7,即3<x<17.
(2)根据三角形三边关系,得3-2<x-1<3+2,解得2<x<6.
(3)根据三角形三边关系,得10-7<x<10+7,即3<x<17,∵ x为最长边,∴ 10≤x<17.
8.设腰长为x,底边为y,根据题意可得,
解得,故该三角形各边长均为6.
由题意解得a=5,b=5,c=7,所以△ABC是等腰三角形.
10.(1)|a-b-c|+|b-c-a|+|c-a-b|=a+b+c;
(2)当a=10,b=8,c=6时,a+b+c=24.
【拓展延伸 能力提升】
1.证明:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD,①
在△PCD中,PC<PD+CD,②
①+②得PB+PD+PC<AB+AD+PD+CD,
即:PB+PC<AB+AC,
即:AB+AC>PB+PC.
2.(1)a=;(2)c = 5-b;
(3)由三角形的三边关系,得当5-b≥,即b≤时,b<5-b+,且b>5-b-,解得<b≤;
当5-b<时,即b>时,则b<5-b+,且b>-(5-b),解得<b<;
∴ b的取值范围为<b<.
·11.1与三角形有关的线段·
第一课时 三角形的边
学案
班级: 课时: 成绩:
学习目标
1.通过具体实例,进一步认识三角形的概念及其基本要素;
2.理解三角形的对边与对角的关系,掌握其三边之间的关系;
3.能将三角形按边分类.
知识构建
【自主学习】
请找出下列图片中的三角形,并将其画出.
【合作探究】
1.由 的三条线段 所组成的图形,叫做三角形.
2.判断下列图形是否为三角形.
3.组成三角形的 叫做三角形的边.
4.三角形相邻两边组成的角叫做三角形的 .简称 .
5.在△ABC中,
(1)AB边所对的角是: ,∠C所对的边是: ;
(2)BC边所对的角是: ,∠A所对的边是: ;
(3)AC边所对的角是: ,∠B所对的边是: .
6.三角形按角分类可分为 .
7.三角形如果按边进行分类,该如何分类?请在以下圆形中进行划分.
三角形
8.在A点的小狗,为了尽快吃到B点的香肠,它选择A→B路线,而不选择A→C→B路线,这体现了 的数学原理.
9.三角形两边的和 第三边,三角形两边的差 第三边.
层级练习
【应用迁移 巩固提高】
1.图中共有 个三角形,它们分别是 :_________________________________________.
2.现有四根长度分别为 2 cm,3 cm,4 cm,5 cm 的小木棍,从中任意取3根. 能搭成多少个不同的三角形?
3.用一条长为 18 cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是 4 cm 的等腰三角形吗?为什么?
【随堂练习 巩固新知】
1.如图所示,图中有 个三角形;其中以AB为边的三角形为 ,含∠OCB的三角形为 ;在△BOC中,OC的对角是 ,∠OCB的对边是 .
2.(2020春 浦东新区期末)设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形.下列四个图中,能正确表示它们之间关系的是( )
3. 下列各组线段能组成一个三角形的是( )
A.3 cm,3 cm,6 cm B.2 cm,3 cm,6 cm
C.5 cm,8 cm,12 cm D.4 cm,7 cm,11 cm
4.图中有几个三角形?用符号表示这些三角形.
5.一个三角形两边分别为3和7,第三边为偶数,第三边长为__________.
【当堂检测 及时反馈】
1.(2020 浙江自主招生)如图,称有一条公共边的两个三角形为一对共边三角形,则图中的共边三角形有( )对
A.8 B.16 C.24 D.32
2.(2019 浦东新区期末)若△ABC三条边的长度分别为m,n,p,且|m-n|+(n-p)2 = 0,则这个三角形为( )
A.等腰三角形 B.等边三角形
C.直角三角形 D.等腰直角三角形
3.(2020春 沙坪坝区校级月考)下列各线段中,能与长为4,6的两线段组成三角形的是( )
A.2 B.8 C.10 D.12
4.(2019秋 江城区期末)若三角形的两边长分别为3和5,则其周长c的取值范围是( )
A.6<c<15 B.6<c<16
C.11<c<13 D.10<c<16
5. (2019春 无锡期中)如图,用四条线段首尾相接连成一个框架,其中AB = 12、BC = 14、CD = 18、DA = 24,则A、B、C、D任意两点之间的最长距离为 .
6.(2019秋 曾都区期末)我们定义三边长均为整数的三角形叫做整三角形.已知△ABC是整三角形,其周长为偶数,若AC-BC = 3.则边长AB的最小值是 .
7.(1)若三角形三条边的长分别是7,10,x,求x的范围.
(2)若三边分别为2,x-1,3,求x 的范围.
(3)若三角形两边长为7和10,求最长边x的范围.
8.一个等腰三角形的周长为18,若腰长的3倍比底边的2倍多6,求各边长.
9.(2019 嘉祥镇期中)已知a,b,c是△ABC的三边长,且b、c满足(b-5)+= 0,a为方程|a-3|= 2的解,求△ABC的周长,并判断△ABC的形状.
10.(2019秋 宜昌期中)已知a,b,c是三角形的三边长.
(1)化简:|a-b-c|+|b-c-a|+|c-a-b|;
(2)在(1)的条件下,若a=10,b=8,c=6,求这个式子.
【拓展延伸 能力提升】
1.已知:如图,P是△ABC内一点.请想一个办法说明AB+AC>PB+PC.
2.小明和小红在一本数学资料书上看到有这样一道竞赛题:“已知△ABC的三边长分别为a,b,c,且|b+c-2a|+(b+c-5)2= 0,求b的取值范围”.
(1)小明说:“b的取值范围,我看不出如何求,但我能求出a的长度.”你知道小明是如何计算的吗?帮他写出求解的过程.
(2)小红说:“我也看不出如何求b的范围,但我能用含b的代数式表示c”.帮小红写出过程.
(3)小明和小红一起去问数学老师,老师说:“根据你们二人的求解,利用书上三角形的三边满足的关系,即可求出答案.”你知道答案吗?请写出过程.
四、参考答案
【自主学习】
1.略.
【合作探究】
1.不在同一条直线上;首尾顺次相接.
2.是;否;否.
3.三条线段.
4.内角;三角形的角.
5.∠C;AB;∠A;BC;∠B;AC.
6.直角三角形、锐角三角形、钝角三角形.
7.
8.两点之间线段最短.
9.大于;小于.
【层级练习】
【应用迁移 巩固提高】
1.5;△ABE,△CDE,△BCE,△ABC,△BCD.
2.可以组成3个不同的三角形.分别是2 cm,3 cm,4 cm ;2 cm,4 cm,5 cm ;3 cm,4 cm,5 cm .
3.(1)三边长分别为 3.6 cm,7.2 cm,7.2 cm.
(2)因为长是 4 cm 的边可能是腰,也可能是底边,所以需要分情况讨论.
如果 4 cm 长的边为底边,腰长为7 cm,
如果 4 cm 长的边为腰,底边为10 cm,不符合三角形两边的和大于第三边.
由上讨论可知,可以围成底边是 4 cm 的等腰三角形.
【随堂练习 巩固新知】
1.8;△ABO、△ABC、△ABD;△BOC、△ABC;∠OBC;OB.
2.C 3.C
4.5个,分别是:△ ABD、△DPC、△CPB、△BCD、△ABC.
5.6或8.
【当堂检测 及时反馈】
1.D 2.B 3.B 4.D 5.32 6.5
7.(1)根据三角形三边关系,得10-7<x<10+7,即3<x<17.
(2)根据三角形三边关系,得3-2<x-1<3+2,解得2<x<6.
(3)根据三角形三边关系,得10-7<x<10+7,即3<x<17,∵ x为最长边,∴ 10≤x<17.
8.设腰长为x,底边为y,根据题意可得,
解得,故该三角形各边长均为6.
由题意解得a=5,b=5,c=7,所以△ABC是等腰三角形.
10.(1)|a-b-c|+|b-c-a|+|c-a-b|=a+b+c;
(2)当a=10,b=8,c=6时,a+b+c=24.
【拓展延伸 能力提升】
1.证明:延长BP交AC于点D,
在△ABD中,PB+PD<AB+AD,①
在△PCD中,PC<PD+CD,②
①+②得PB+PD+PC<AB+AD+PD+CD,
即:PB+PC<AB+AC,
即:AB+AC>PB+PC.
2.(1)a=;(2)c = 5-b;
(3)由三角形的三边关系,得当5-b≥,即b≤时,b<5-b+,且b>5-b-,解得<b≤;
当5-b<时,即b>时,则b<5-b+,且b>-(5-b),解得<b<;
∴ b的取值范围为<b<.
