11.2.3三角形的外角 学案 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.2.3三角形的外角 学案 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 478.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 20:45:36 | ||
图片预览




文档简介
第十一章 三角形
·11.2与三角形有关的角·
第三课时 三角形的外角
学案
班级: 课时: 成绩:
学习目标
1.了解三角形外角的概念.
2.掌握三角形外角的性质的推理过程.
3.能综合利用三角形的内角和定理及外角的性质解决问题.
知识构建
【自主学习】
1.如图,小颖从点A出发,绕着圆形花坛的外围走一圈,那么回到原来位置时,一共转了 度.
2.如果绕着三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时,一共转了 度吗.
3.三角形的 组成的角,叫做三角形的外角.
4.画出△ABC,然后画出它的所有外角,问:
(1)每一个顶点处相对应的外角有 个,它们之间互为 角.
(2)三角形的每一个外角与相邻的内角互为
角.
(3)每一个三角形有 个外角.
5.∠BEC是 的外角,
也是 的内角.
∠BDC是
的内角,也是 的外角.
∠BFC是
的外角,也是 的内角.
【合作探究】
1.如图,在△ABC中,∠A = 70 °,∠B = 60 °.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
2.如图,CD是边BC的延长线,求证:∠ACD =∠A+∠B.
三角形外角的性质:
(1)三角形的外角 与它不相邻的两个内角的和.
(2)三角形的一个外角 任何一个与它不相邻的内角.
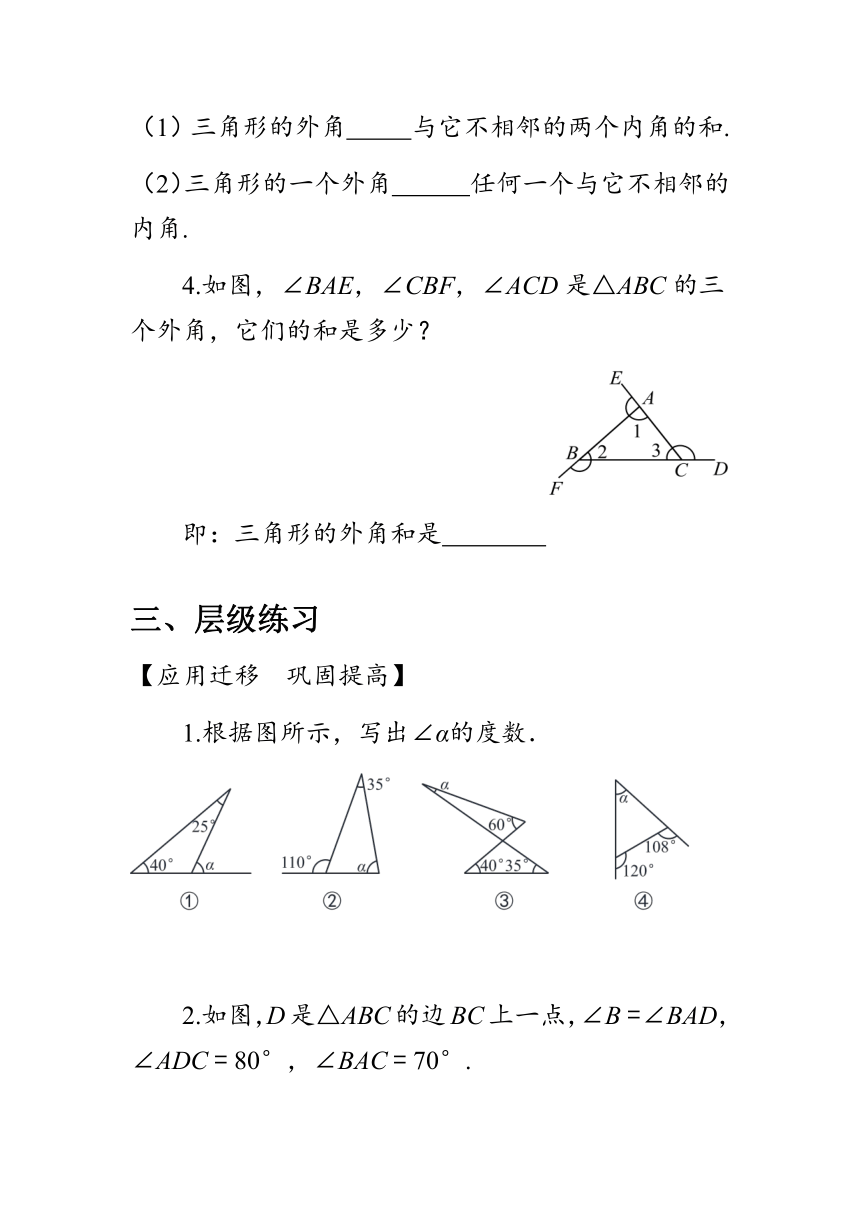
4.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
即:三角形的外角和是
层级练习
【应用迁移 巩固提高】
1.根据图所示,写出∠α的度数.
2.如图,D是△ABC的边BC上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
(1)求∠B的度数;
(2)求∠C的度数.
3.如图,直线AB∥CD,∠A = 70°,∠C = 40°,求∠E的度数.
【随堂练习 巩固新知】
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.
(2)三角形的外角和等于它内角和的 2 倍.
(3)三角形的一个外角等于两个内角的和.
(4)三角形的一个外角等于与它不相邻的两个内角的和.
(5)三角形的一个外角大于任何一个内角.
(6)三角形的一个内角小于任何一个与它不相邻的外角.
2.(2022秋 达孜区期中)如图,∠1、∠2、∠3 中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
4.(2022春 平昌县期末)如图,∠A,∠1,∠2 的大小关系为( )
A.∠A>∠1>∠2 B.∠A>∠2>∠1
C.∠2>∠1>∠A D.∠2>∠A>∠1
5.(2022秋 文山市期末)如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A = 44°,∠1 = 57°,则∠2 = .
【当堂检测 及时反馈】
1.(2022秋 新宾县期末)如图,BP是△ABC中∠ABC 的平分线,CP是∠ACB的外角的平分线,如果∠ABP = 20°,∠ACP = 50°,则∠A =( )
A.60° B.80° C.70° D.50°
2.(2022秋 路北区期末)如图,在△ABC中,∠A = 60 度,点D,E分别在AB,AC上,则∠1+∠2 的大小为多少度( )
A.140 B.190 C.320 D.240
3.(2022 枣庄)将一副直角三角板按如图所示的位置放置,使含 30°角的三角板的一条直角边和含 45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
4.(2022秋 织金县期末)如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2 =∠3+∠4 B.∠1+∠2 =∠4-∠3
C.∠1+∠4 =∠2+∠3 D.∠1+∠4 =∠2-∠3
5.(2022秋 蒙阴县期中)在△ABC中,∠A = 50°,∠B = 30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.60° B.10° C.45° D.10°或 60°
6.(2022秋 金凤区校级期末)如图,∠BCD = 150°,则∠A+∠B+∠D的度数为 .
7.有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F = 度.
8.求∠A +∠B +∠C +∠D +∠E的度数.
9.(2022秋 香洲区校级月考)一个零件的形状如图所示,按规定∠A = 90°,∠B和∠C分别是 32°和 21°的零件为合格零件,现质检工人量得∠BDC = 149°,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
10.(2022秋 汉滨区校级月考)已知:BP、CP是△ABC的外角的平分线,交于点P.求证:∠P = 90°- ∠A.
【拓展延伸 能力提升】
1.如图,D、E分别在BC、AC上,AD、BE交于F.求证:
(1)∠AFB>∠C;
(2)∠AFB =∠1+∠2+∠C.
2.(2020秋 彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A = 50°,则∠D = ;
(2)若∠A = 80°,则∠D = ;
(3)若∠A = 130°,则∠D = ;
(4)若∠D = 36°,则∠A = ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
四、参考答案
【自主学习】
1.360. 2.360. 3.一边与另一边的延长线.
4.画图略,(1)2,对顶,(2)邻补,(3)6.
5.△AEB,△BEC、△EFC,△BDC、△BDF,△ADC,△BDF 、△CEF,△BFC.
【合作探究】
1.解:由∠A +∠B +∠ACB = 180°,得∠ACB = 180°-∠A-∠B = 50°.
由∠ACB +∠ACD = 180°,得∠ACD = 180°-(180°-∠A-∠B)= ∠A +∠B = 130°.
2.
3.(1)等于,(2)大于.
4.解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE =∠2+∠3,∠CBF =∠1+∠3,∠ACD =∠1+∠2.
所以∠BAE+∠CBF+∠ACD = 2(∠1+∠2+∠3).
由∠1+∠2+∠3 = 180°,得
∠BAE+∠CBF+∠ACD = 360°.
360°.
【层级练习】
【应用迁移 巩固提高】
1.解:①∠α = 25°+40°= 65°;
②∠α = 110°-35°= 75°;
③∠α = 40°+35°-60°= 15°;
④∠α = 180°-(360°-120°-108°)= 48°.
2.解:(1)∵ ∠ADC是△ABD的外角,
∴ ∠ADC =∠B +∠BAD = 80°.
又∵ ∠B =∠BAD,
∴ ∠B = 80°×= 40°.
(2)在△ABC中,∠B+∠BAC+∠C = 180°,
由(1)得,∠B = 40°,
∴ ∠C = 180°-40°-70 °= 70°.
3.解:如图所示,标出∠1和∠2.
∵ AB∥CD,
∠1 =∠A = 70°.
∴根据三角形外角性质,得
∠E =∠1-∠C = 70°- 40°= 30°.
【随堂练习 巩固新知】
(1)×(2)√(3)×(4)√(5)×(6)√
C 3.C 4.C 5.101°
【当堂检测 及时反馈】
A 2.D 3.C 4.D 5.D
6.150° 7.360
8.解:∵ ∠1 是△FBE的外角,
∴ ∠1 =∠B+∠E.
同理∠2 =∠A+∠D,
在△CFG中∠C+∠1+∠2 = 180°,
∴ ∠A+∠B+∠C+∠D+∠E = 180°.
9.解:如图,延长BD交AC于E,
∵ ∠A = 90°,∠B = 32°,
∴ ∠DEC =∠A+∠B = 90°+32°= 122°,
∵ ∠C = 21°,
∴ ∠BDC =∠C +∠DEC = 21°+122°= 143°.
又∵ 质检工人量得∠BDC = 149°,
∴ 这个零件不合格.
10.证明:∵ BP、CP是△ABC的外角的平分线,
∴ ∠PCB =∠MCB,∠PBC =∠NBC,
∵ ∠MCB =∠A+∠ABC,∠NBC =∠A+∠ACB,
∴ ∠PCB+∠PBC =(∠A+∠ABC+∠A+∠ACB)= (180°+∠A)= 90°+ ∠A,
∴ ∠P = 180°-(∠PCB+∠PBC)= 180°﹣(90°+ ∠A)= 90°-∠A.
【拓展延伸 能力提升】
1.证明:(1)∵ ∠AFB是△AEF的一个外角,
∴ ∠AFB>∠AEF.
∵ ∠AEF是△BCE的一个外角,
∴ ∠AEF>∠C,∴ ∠AFB>∠C.
(2)∵ ∠AFB =∠AEB+∠1,
∠AEB =∠C+∠2,
∴ ∠AFB =∠1+∠C+∠2.
2.(1)25°,(2)40°,(3)65°,(4)72°,
(5)∠D =∠A.
理由如下:∵ BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴ ∠ACE = 2∠2,∠ABC = 2∠1,
∵ ∠ACE =∠ABC+∠A,
∴ 2∠2 = 2∠1+∠A,
而∠2 =∠1+∠D,
∴ 2∠2 = 2∠1+2∠D,
∴ ∠A = 2∠D,
即∠D =∠A.
·11.2与三角形有关的角·
第三课时 三角形的外角
学案
班级: 课时: 成绩:
学习目标
1.了解三角形外角的概念.
2.掌握三角形外角的性质的推理过程.
3.能综合利用三角形的内角和定理及外角的性质解决问题.
知识构建
【自主学习】
1.如图,小颖从点A出发,绕着圆形花坛的外围走一圈,那么回到原来位置时,一共转了 度.
2.如果绕着三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时,一共转了 度吗.
3.三角形的 组成的角,叫做三角形的外角.
4.画出△ABC,然后画出它的所有外角,问:
(1)每一个顶点处相对应的外角有 个,它们之间互为 角.
(2)三角形的每一个外角与相邻的内角互为
角.
(3)每一个三角形有 个外角.
5.∠BEC是 的外角,
也是 的内角.
∠BDC是
的内角,也是 的外角.
∠BFC是
的外角,也是 的内角.
【合作探究】
1.如图,在△ABC中,∠A = 70 °,∠B = 60 °.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
2.如图,CD是边BC的延长线,求证:∠ACD =∠A+∠B.
三角形外角的性质:
(1)三角形的外角 与它不相邻的两个内角的和.
(2)三角形的一个外角 任何一个与它不相邻的内角.
4.如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
即:三角形的外角和是
层级练习
【应用迁移 巩固提高】
1.根据图所示,写出∠α的度数.
2.如图,D是△ABC的边BC上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
(1)求∠B的度数;
(2)求∠C的度数.
3.如图,直线AB∥CD,∠A = 70°,∠C = 40°,求∠E的度数.
【随堂练习 巩固新知】
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.
(2)三角形的外角和等于它内角和的 2 倍.
(3)三角形的一个外角等于两个内角的和.
(4)三角形的一个外角等于与它不相邻的两个内角的和.
(5)三角形的一个外角大于任何一个内角.
(6)三角形的一个内角小于任何一个与它不相邻的外角.
2.(2022秋 达孜区期中)如图,∠1、∠2、∠3 中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
4.(2022春 平昌县期末)如图,∠A,∠1,∠2 的大小关系为( )
A.∠A>∠1>∠2 B.∠A>∠2>∠1
C.∠2>∠1>∠A D.∠2>∠A>∠1
5.(2022秋 文山市期末)如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A = 44°,∠1 = 57°,则∠2 = .
【当堂检测 及时反馈】
1.(2022秋 新宾县期末)如图,BP是△ABC中∠ABC 的平分线,CP是∠ACB的外角的平分线,如果∠ABP = 20°,∠ACP = 50°,则∠A =( )
A.60° B.80° C.70° D.50°
2.(2022秋 路北区期末)如图,在△ABC中,∠A = 60 度,点D,E分别在AB,AC上,则∠1+∠2 的大小为多少度( )
A.140 B.190 C.320 D.240
3.(2022 枣庄)将一副直角三角板按如图所示的位置放置,使含 30°角的三角板的一条直角边和含 45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
4.(2022秋 织金县期末)如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2 =∠3+∠4 B.∠1+∠2 =∠4-∠3
C.∠1+∠4 =∠2+∠3 D.∠1+∠4 =∠2-∠3
5.(2022秋 蒙阴县期中)在△ABC中,∠A = 50°,∠B = 30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.60° B.10° C.45° D.10°或 60°
6.(2022秋 金凤区校级期末)如图,∠BCD = 150°,则∠A+∠B+∠D的度数为 .
7.有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F = 度.
8.求∠A +∠B +∠C +∠D +∠E的度数.
9.(2022秋 香洲区校级月考)一个零件的形状如图所示,按规定∠A = 90°,∠B和∠C分别是 32°和 21°的零件为合格零件,现质检工人量得∠BDC = 149°,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
10.(2022秋 汉滨区校级月考)已知:BP、CP是△ABC的外角的平分线,交于点P.求证:∠P = 90°- ∠A.
【拓展延伸 能力提升】
1.如图,D、E分别在BC、AC上,AD、BE交于F.求证:
(1)∠AFB>∠C;
(2)∠AFB =∠1+∠2+∠C.
2.(2020秋 彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A = 50°,则∠D = ;
(2)若∠A = 80°,则∠D = ;
(3)若∠A = 130°,则∠D = ;
(4)若∠D = 36°,则∠A = ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
四、参考答案
【自主学习】
1.360. 2.360. 3.一边与另一边的延长线.
4.画图略,(1)2,对顶,(2)邻补,(3)6.
5.△AEB,△BEC、△EFC,△BDC、△BDF,△ADC,△BDF 、△CEF,△BFC.
【合作探究】
1.解:由∠A +∠B +∠ACB = 180°,得∠ACB = 180°-∠A-∠B = 50°.
由∠ACB +∠ACD = 180°,得∠ACD = 180°-(180°-∠A-∠B)= ∠A +∠B = 130°.
2.
3.(1)等于,(2)大于.
4.解:由三角形的一个外角等于与它不相邻的两个内角的和,得∠BAE =∠2+∠3,∠CBF =∠1+∠3,∠ACD =∠1+∠2.
所以∠BAE+∠CBF+∠ACD = 2(∠1+∠2+∠3).
由∠1+∠2+∠3 = 180°,得
∠BAE+∠CBF+∠ACD = 360°.
360°.
【层级练习】
【应用迁移 巩固提高】
1.解:①∠α = 25°+40°= 65°;
②∠α = 110°-35°= 75°;
③∠α = 40°+35°-60°= 15°;
④∠α = 180°-(360°-120°-108°)= 48°.
2.解:(1)∵ ∠ADC是△ABD的外角,
∴ ∠ADC =∠B +∠BAD = 80°.
又∵ ∠B =∠BAD,
∴ ∠B = 80°×= 40°.
(2)在△ABC中,∠B+∠BAC+∠C = 180°,
由(1)得,∠B = 40°,
∴ ∠C = 180°-40°-70 °= 70°.
3.解:如图所示,标出∠1和∠2.
∵ AB∥CD,
∠1 =∠A = 70°.
∴根据三角形外角性质,得
∠E =∠1-∠C = 70°- 40°= 30°.
【随堂练习 巩固新知】
(1)×(2)√(3)×(4)√(5)×(6)√
C 3.C 4.C 5.101°
【当堂检测 及时反馈】
A 2.D 3.C 4.D 5.D
6.150° 7.360
8.解:∵ ∠1 是△FBE的外角,
∴ ∠1 =∠B+∠E.
同理∠2 =∠A+∠D,
在△CFG中∠C+∠1+∠2 = 180°,
∴ ∠A+∠B+∠C+∠D+∠E = 180°.
9.解:如图,延长BD交AC于E,
∵ ∠A = 90°,∠B = 32°,
∴ ∠DEC =∠A+∠B = 90°+32°= 122°,
∵ ∠C = 21°,
∴ ∠BDC =∠C +∠DEC = 21°+122°= 143°.
又∵ 质检工人量得∠BDC = 149°,
∴ 这个零件不合格.
10.证明:∵ BP、CP是△ABC的外角的平分线,
∴ ∠PCB =∠MCB,∠PBC =∠NBC,
∵ ∠MCB =∠A+∠ABC,∠NBC =∠A+∠ACB,
∴ ∠PCB+∠PBC =(∠A+∠ABC+∠A+∠ACB)= (180°+∠A)= 90°+ ∠A,
∴ ∠P = 180°-(∠PCB+∠PBC)= 180°﹣(90°+ ∠A)= 90°-∠A.
【拓展延伸 能力提升】
1.证明:(1)∵ ∠AFB是△AEF的一个外角,
∴ ∠AFB>∠AEF.
∵ ∠AEF是△BCE的一个外角,
∴ ∠AEF>∠C,∴ ∠AFB>∠C.
(2)∵ ∠AFB =∠AEB+∠1,
∠AEB =∠C+∠2,
∴ ∠AFB =∠1+∠C+∠2.
2.(1)25°,(2)40°,(3)65°,(4)72°,
(5)∠D =∠A.
理由如下:∵ BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴ ∠ACE = 2∠2,∠ABC = 2∠1,
∵ ∠ACE =∠ABC+∠A,
∴ 2∠2 = 2∠1+∠A,
而∠2 =∠1+∠D,
∴ 2∠2 = 2∠1+2∠D,
∴ ∠A = 2∠D,
即∠D =∠A.
