11.1.2三角形的高、中线与角平分线 作业 2023-2024学年人教版八年级数学上册
文档属性
| 名称 | 11.1.2三角形的高、中线与角平分线 作业 2023-2024学年人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 268.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 20:46:34 | ||
图片预览



文档简介
11.1 与三角形有关的线段
·第2课时
三角形的高、中位线与角平分线·
课后作业(1)
班级:____ 姓名:_____ 难易度:★☆☆
一、选择题
1.如图所示,△ABC中AC边上的高线是( )
A.线段DA B.线段BA
C.线段BC D.线段BD
2.下列说法错误的是( )
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
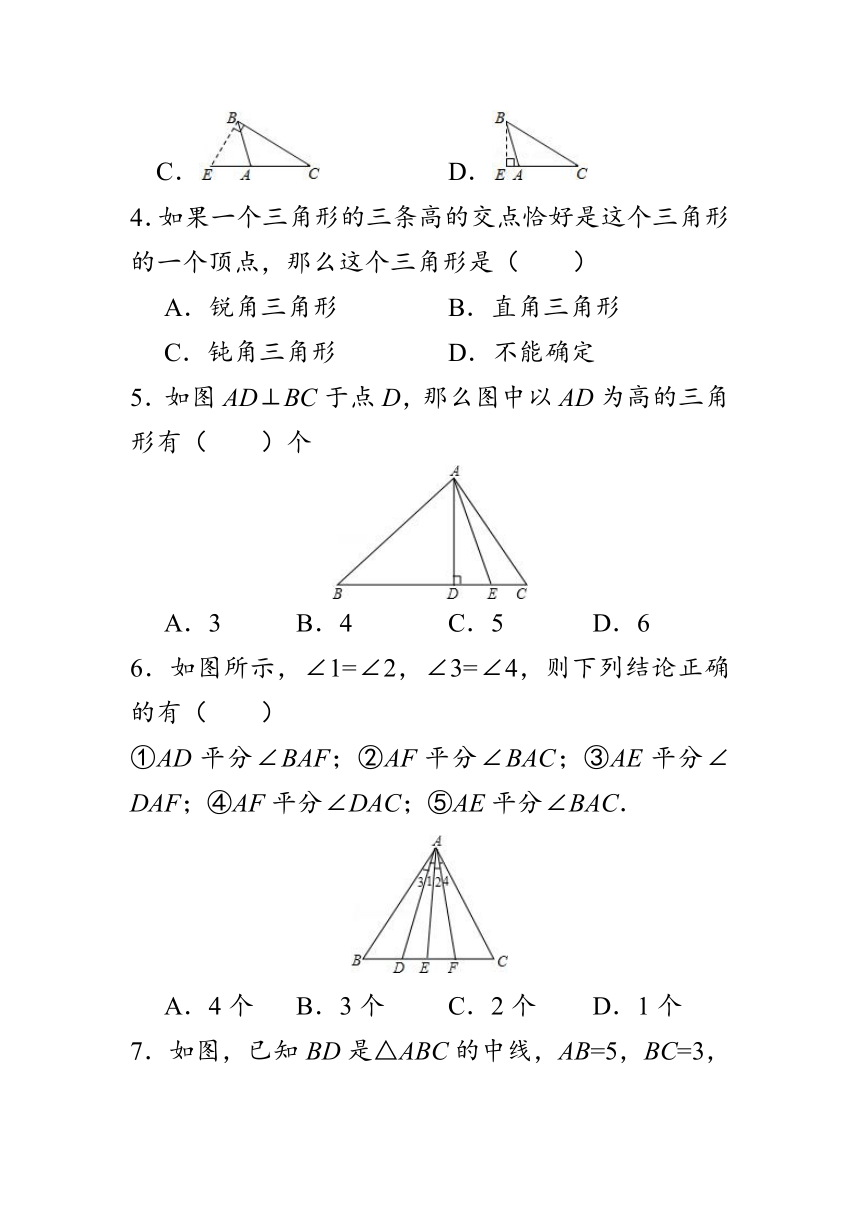
3.下列各图中,正确画出AC边上的高的是( )
A. B.
C. D.
4.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
5.如图AD⊥BC于点D,那么图中以AD为高的三角形有( )个
A.3 B.4 C.5 D.6
6.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A.4个 B.3个 C.2个 D.1个
7.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是( )
A.9 B.14 C.16 D.不能确定
8.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
AD是△ABE的角平分线
B.BE是△ABD边AD上的中线
C.CH为△ACD边AD上的高
D.AH为△ABC的角平分线
二、填空题
1.如图,在线段AD,AE,AF中,△ABC的高是线段 .
2.如图所示:在△AEC中,AE边上的高是 .
3.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
4.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
5.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于 .
三、解答题
1.已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.
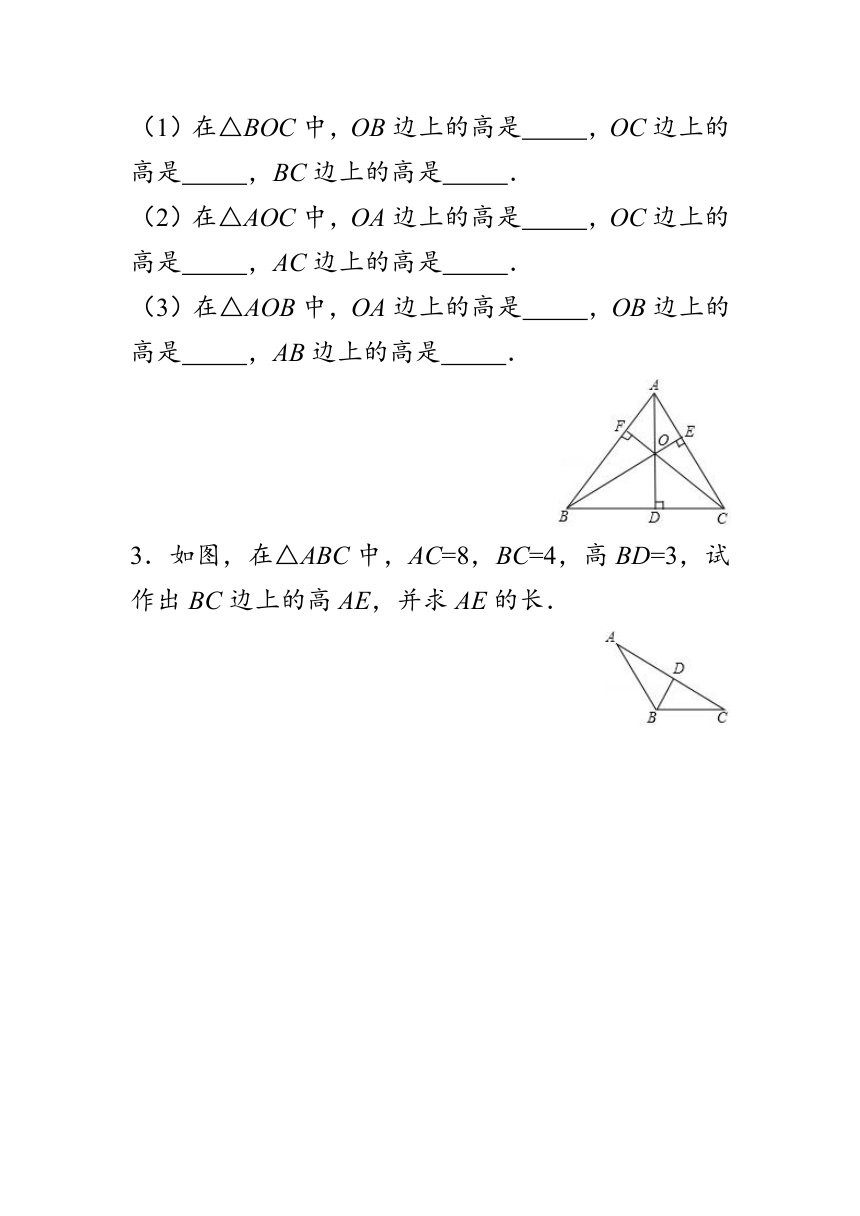
2.如图,△ABC的三条高AD、BE、CF相交于点O.
(1)在△BOC中,OB边上的高是 ,OC边上的高是 ,BC边上的高是 .
(2)在△AOC中,OA边上的高是 ,OC边上的高是 ,AC边上的高是 .
(3)在△AOB中,OA边上的高是 ,OB边上的高是 ,AB边上的高是 .
3.如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长.
课后作业(2)
班级:____ 姓名:_____ 难易度:★★☆
一、选择题
1.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
2.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
3.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
4.如图,AC⊥BC,CD⊥AB,DE⊥BC,分别交BC,AB,BC于点C,D,E,则下列说法中不正确的是( )
AC是△ABC和△ABE的高
DE,DC都是△BCD的高
C.DE是△DBE和△ABE的高
D.AD,CD都是△ACD的高
5.如图,已知BD=CD,则AD一定是△ABC的( )
A.角平分线 B.高线 C.中线 D.无法确定
6.如图所示,AC⊥BC于C,CD⊥AB于D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
7.如图,△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,( )
A.AD是△ABC的高 B.EB是△ABC的高
C.FC是△ABC的高 D.AE、AF是△ABC的高
8.如图,AD是△ABC的中线,已知△ABD的周长为22cm,AB比AC长3cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
1.锐角三角形的三条高都在 ,钝角三角形有 条高在三角形外,直角三角形有两条高恰是它的 .
2.如图,已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4cm.若AB=16cm,那么AC=
cm.
3.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段 是△ABC中AC边上的高.
4.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
5.如图,AD⊥BC于D,那么图中以AD为高的三角形有 个.
三、解答题
1.如图所示,AD,CE是△ABC的两条高,AB=4cm,BC=8cm,CE=6cm,求AD的长.
2.如图,△ABC中,∠ACB=90°,CD、CE、CF分别是△ABC的高、中线、角平分线.求证:∠1=∠2.
3.如图,在△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长.
课后作业(3)
班级:____ 姓名:_____ 难易度:★★★
一、选择题
1.三角形的高线、中线、角平分线都是( )
A.直线 B.线段
C.射线 D.以上情况都有
2.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A. B.
C. D.
3.在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多3,AB与AC的和为13,则AC的长为( )
A.7 B.8 C.9 D.10
4.如图所示,有一条线段是△ABC(AC>AB)的中线,该线段是( )
线段AD B.线段AE
C.线段 AF D.线段MN
5.如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,其中正确的个数是( )
①BG是△ABD中边AD上的中线;
②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;
③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线.
A.0 B.1 C.2 D.3
6.如图,已知P为直线l外一点,点A、B、C、D在直线l上,且PA>PB>PC>PD,下列说法正确的是( )
A.线段PD的长是点P到直线l的距离
B.线段PC可能是△PAB的高
C.线段PD可能是△PBC的高
D.线段PB可能是△PAC的高
7.如图,AD是△ABC的中线,则下列结论正确的是( )
AD⊥BC B.∠BAD=∠CAD
C.AB=AC D.BD=CD
8.若线段AM、AN分别是△ABC中BC边上的高线和中线,则( )
A.AM>AN B.AM>AN或AM=AN
C.AM<AN D.AM<AN或AM=AN
二、填空题
1.如图,以AD为高的三角形共有 个.
2.如图,已知BE⊥AD,CF⊥AD,且BE=CF.那么AD是△ABC的 .(填“中线”或“角平分线”)
3.如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为 cm.
4.在△ABC中,AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,则AC= ,AB= .
5.如图,在△ABC,AD是角平分线,AE是中线.AF是高,如果BC=10cm,那么BE= ;∠ABC=40°,∠ACB=60°,那么∠BAD= ,∠DAF= .
三、解答题
1.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
2.如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗?说明理由.
3.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
【参考答案】
课后作业(1)
一、1.D 2.A 3.D 4.B 5.D 6.C 7.A 8.C
二、1.AF 2.CD 3.50° 4.9 5.2
三、1.由题意画图可得:
2.CE,BF,OD;CD,AF,OE;BD,AE,OF.
3.如图,过点A作BC边上的高线AE,交CB延长线于点E.∵BC AE=AC BD,AC=8,BC=4,高BD=3,
∴×4AE=×8×3,
则AE=6.
课后作业(2)
一、1.B 2.B 3.B 4.C 5.C 6.D 7.A 8.A
二、1.三角形内部;二;直角边. 2.12 3.BE 4.45° 5.6
三、1.AD=3cm.
2.证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF.
∵CD⊥AB,∠ACB=90°,
∴∠ACD=∠B(同角的余角相等).
∵CE是AB边上的中线,
∴BE=CE,
∴∠BCE=∠B(等边对等角),
∴∠1=∠ACF-∠ACD=∠ACF-∠B,
∠2=∠BCF-∠BCE=∠ACF-∠B,
∴∠1=∠2.
3.AB=24,BC=14.
课后作业(3)
一、1.B 2.A 3.B 4.C 5.C 6.C 7.D 8.D
二、1.6 2.中线 3.2 4.48;28 5.5cm;40°;10°.
三、1.(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
CD=.
2.AD是△ABC的角平分线.
理由:∵DE∥AC,DF∥AB,
∴∠ADE=∠DAF,∠ADF=∠EAD,
又∵∠ADE=∠ADF,
∴∠DAF=∠EAD,
又∵∠DAF+∠EAD=∠BAC,
∴AD是∠BAC的角平分线.
3.AC=9cm.
·第2课时
三角形的高、中位线与角平分线·
课后作业(1)
班级:____ 姓名:_____ 难易度:★☆☆
一、选择题
1.如图所示,△ABC中AC边上的高线是( )
A.线段DA B.线段BA
C.线段BC D.线段BD
2.下列说法错误的是( )
A.三角形三条高交于三角形内一点
B.三角形三条中线交于三角形内一点
C.三角形三条角平分线交于三角形内一点
D.三角形的中线、角平分线、高都是线段
3.下列各图中,正确画出AC边上的高的是( )
A. B.
C. D.
4.如果一个三角形的三条高的交点恰好是这个三角形的一个顶点,那么这个三角形是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
5.如图AD⊥BC于点D,那么图中以AD为高的三角形有( )个
A.3 B.4 C.5 D.6
6.如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( )
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A.4个 B.3个 C.2个 D.1个
7.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是( )
A.9 B.14 C.16 D.不能确定
8.如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于E.F为AB上的一点,CF⊥AD于H.下列判断正确的有( )
AD是△ABE的角平分线
B.BE是△ABD边AD上的中线
C.CH为△ACD边AD上的高
D.AH为△ABC的角平分线
二、填空题
1.如图,在线段AD,AE,AF中,△ABC的高是线段 .
2.如图所示:在△AEC中,AE边上的高是 .
3.如图,在△ABC中,AD⊥BC,AE平分∠BAC,若∠1=30°,∠2=20°,则∠B= .
4.如图,已知BD是△ABC的中线,AB=5,BC=3,且△ABD的周长为11,则△BCD的周长是 .
5.若△ABC中,∠ACB是钝角,AD是BC边上的高,若AD=2,BD=3.CD=1,则△ABC的面积等于 .
三、解答题
1.已知△ABC,如图,过点A画△ABC的角平分线AD、中线AE和高线AF.
2.如图,△ABC的三条高AD、BE、CF相交于点O.
(1)在△BOC中,OB边上的高是 ,OC边上的高是 ,BC边上的高是 .
(2)在△AOC中,OA边上的高是 ,OC边上的高是 ,AC边上的高是 .
(3)在△AOB中,OA边上的高是 ,OB边上的高是 ,AB边上的高是 .
3.如图,在△ABC中,AC=8,BC=4,高BD=3,试作出BC边上的高AE,并求AE的长.
课后作业(2)
班级:____ 姓名:_____ 难易度:★★☆
一、选择题
1.如图所示在△ABC中,AB边上的高线画法正确的是( )
A. B.
C. D.
2.三角形一边上的中线把原三角形分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形
3.如图,AD⊥BC,GC⊥BC,CF⊥AB,垂足分别是D、C、F,下列说法中,错误的是( )
A.△ABC中,AD是边BC上的高
B.△ABC中,GC是边BC上的高
C.△GBC中,GC是边BC上的高
D.△GBC中,CF是边BG上的高
4.如图,AC⊥BC,CD⊥AB,DE⊥BC,分别交BC,AB,BC于点C,D,E,则下列说法中不正确的是( )
AC是△ABC和△ABE的高
DE,DC都是△BCD的高
C.DE是△DBE和△ABE的高
D.AD,CD都是△ACD的高
5.如图,已知BD=CD,则AD一定是△ABC的( )
A.角平分线 B.高线 C.中线 D.无法确定
6.如图所示,AC⊥BC于C,CD⊥AB于D,图中可以作为三角形“高”的线段有( )
A.1条 B.2条 C.3条 D.5条
7.如图,△ABC中,∠BAC是钝角,AD⊥BC、EB⊥BC、FC⊥BC,( )
A.AD是△ABC的高 B.EB是△ABC的高
C.FC是△ABC的高 D.AE、AF是△ABC的高
8.如图,AD是△ABC的中线,已知△ABD的周长为22cm,AB比AC长3cm,则△ACD的周长为( )
A.19cm B.22cm C.25cm D.31cm
二、填空题
1.锐角三角形的三条高都在 ,钝角三角形有 条高在三角形外,直角三角形有两条高恰是它的 .
2.如图,已知AD是△ABC的中线,且△ABD的周长比△ACD的周长多4cm.若AB=16cm,那么AC=
cm.
3.如图,△ABC中,∠ACB>90°,AD⊥BC,BE⊥AC,CF⊥AB,垂足分别为D、E、F,则线段 是△ABC中AC边上的高.
4.如图,在△ABC中,∠ACB=60°,∠BAC=75°,AD⊥BC于D,BE⊥AC于E,AD与BE交于H,则∠CHD= .
5.如图,AD⊥BC于D,那么图中以AD为高的三角形有 个.
三、解答题
1.如图所示,AD,CE是△ABC的两条高,AB=4cm,BC=8cm,CE=6cm,求AD的长.
2.如图,△ABC中,∠ACB=90°,CD、CE、CF分别是△ABC的高、中线、角平分线.求证:∠1=∠2.
3.如图,在△ABC中(AB>BC),AB=2AC,AC边上中线BD把△ABC的周长分成30和20两部分,求AB和BC的长.
课后作业(3)
班级:____ 姓名:_____ 难易度:★★★
一、选择题
1.三角形的高线、中线、角平分线都是( )
A.直线 B.线段
C.射线 D.以上情况都有
2.用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )
A. B.
C. D.
3.在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多3,AB与AC的和为13,则AC的长为( )
A.7 B.8 C.9 D.10
4.如图所示,有一条线段是△ABC(AC>AB)的中线,该线段是( )
线段AD B.线段AE
C.线段 AF D.线段MN
5.如图,△ABC中,∠1=∠2,G为AD中点,延长BG交AC于E,F为AB上一点,且CF⊥AD于H,下列判断,其中正确的个数是( )
①BG是△ABD中边AD上的中线;
②AD既是△ABC中∠BAC的角平分线,也是△ABE中∠BAE的角平分线;
③CH既是△ACD中AD边上的高线,也是△ACH中AH边上的高线.
A.0 B.1 C.2 D.3
6.如图,已知P为直线l外一点,点A、B、C、D在直线l上,且PA>PB>PC>PD,下列说法正确的是( )
A.线段PD的长是点P到直线l的距离
B.线段PC可能是△PAB的高
C.线段PD可能是△PBC的高
D.线段PB可能是△PAC的高
7.如图,AD是△ABC的中线,则下列结论正确的是( )
AD⊥BC B.∠BAD=∠CAD
C.AB=AC D.BD=CD
8.若线段AM、AN分别是△ABC中BC边上的高线和中线,则( )
A.AM>AN B.AM>AN或AM=AN
C.AM<AN D.AM<AN或AM=AN
二、填空题
1.如图,以AD为高的三角形共有 个.
2.如图,已知BE⊥AD,CF⊥AD,且BE=CF.那么AD是△ABC的 .(填“中线”或“角平分线”)
3.如图,BD是△ABC的中线,AB=6cm,BC=4cm,则△ABD和△BCD的周长差为 cm.
4.在△ABC中,AC=2BC,BC边上的中线AD把△ABC的周长分成60和40两部分,则AC= ,AB= .
5.如图,在△ABC,AD是角平分线,AE是中线.AF是高,如果BC=10cm,那么BE= ;∠ABC=40°,∠ACB=60°,那么∠BAD= ,∠DAF= .
三、解答题
1.如图,△ACB中,∠ACB=90°,∠1=∠B.
(1)试说明CD是△ABC的高;
(2)如果AC=8,BC=6,AB=10,求CD的长.
2.如图,D是△ABC中BC上的一点,DE∥AC交AB于点E,DF∥AB交AC于点F,且∠ADE=∠ADF,AD是△ABC的角平分线吗?说明理由.
3.如图,在△ABC中,AD是BC边上的中线,△ADC的周长比△ABD的周长多5cm,AB与AC的和为13cm,求AC的长.
【参考答案】
课后作业(1)
一、1.D 2.A 3.D 4.B 5.D 6.C 7.A 8.C
二、1.AF 2.CD 3.50° 4.9 5.2
三、1.由题意画图可得:
2.CE,BF,OD;CD,AF,OE;BD,AE,OF.
3.如图,过点A作BC边上的高线AE,交CB延长线于点E.∵BC AE=AC BD,AC=8,BC=4,高BD=3,
∴×4AE=×8×3,
则AE=6.
课后作业(2)
一、1.B 2.B 3.B 4.C 5.C 6.D 7.A 8.A
二、1.三角形内部;二;直角边. 2.12 3.BE 4.45° 5.6
三、1.AD=3cm.
2.证明:∵CF是∠ACB的平分线,
∴∠ACF=∠BCF.
∵CD⊥AB,∠ACB=90°,
∴∠ACD=∠B(同角的余角相等).
∵CE是AB边上的中线,
∴BE=CE,
∴∠BCE=∠B(等边对等角),
∴∠1=∠ACF-∠ACD=∠ACF-∠B,
∠2=∠BCF-∠BCE=∠ACF-∠B,
∴∠1=∠2.
3.AB=24,BC=14.
课后作业(3)
一、1.B 2.A 3.B 4.C 5.C 6.C 7.D 8.D
二、1.6 2.中线 3.2 4.48;28 5.5cm;40°;10°.
三、1.(1)∵∠1+∠BCD=90°,∠1=∠B
∴∠B+∠BCD=90°
∴△BDC是直角三角形,即CD⊥AB,
∴CD是△ABC的高;
CD=.
2.AD是△ABC的角平分线.
理由:∵DE∥AC,DF∥AB,
∴∠ADE=∠DAF,∠ADF=∠EAD,
又∵∠ADE=∠ADF,
∴∠DAF=∠EAD,
又∵∠DAF+∠EAD=∠BAC,
∴AD是∠BAC的角平分线.
3.AC=9cm.
