2024年中考数学高频考点专项练习——圆的切线的证明(含答案)
文档属性
| 名称 | 2024年中考数学高频考点专项练习——圆的切线的证明(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 323.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 22:34:51 | ||
图片预览

文档简介
2024年中考数学高频考点专项练习——圆的切线的证明
1.如图,直线AB经过⊙O上的一点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
2.如图,AB是的直径,点F在上,∠BAF的平分线AE交于点E,过点E作,交AF的延长线于点D,延长DE、AB相交于点C.求证:CD是的切线;
3.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
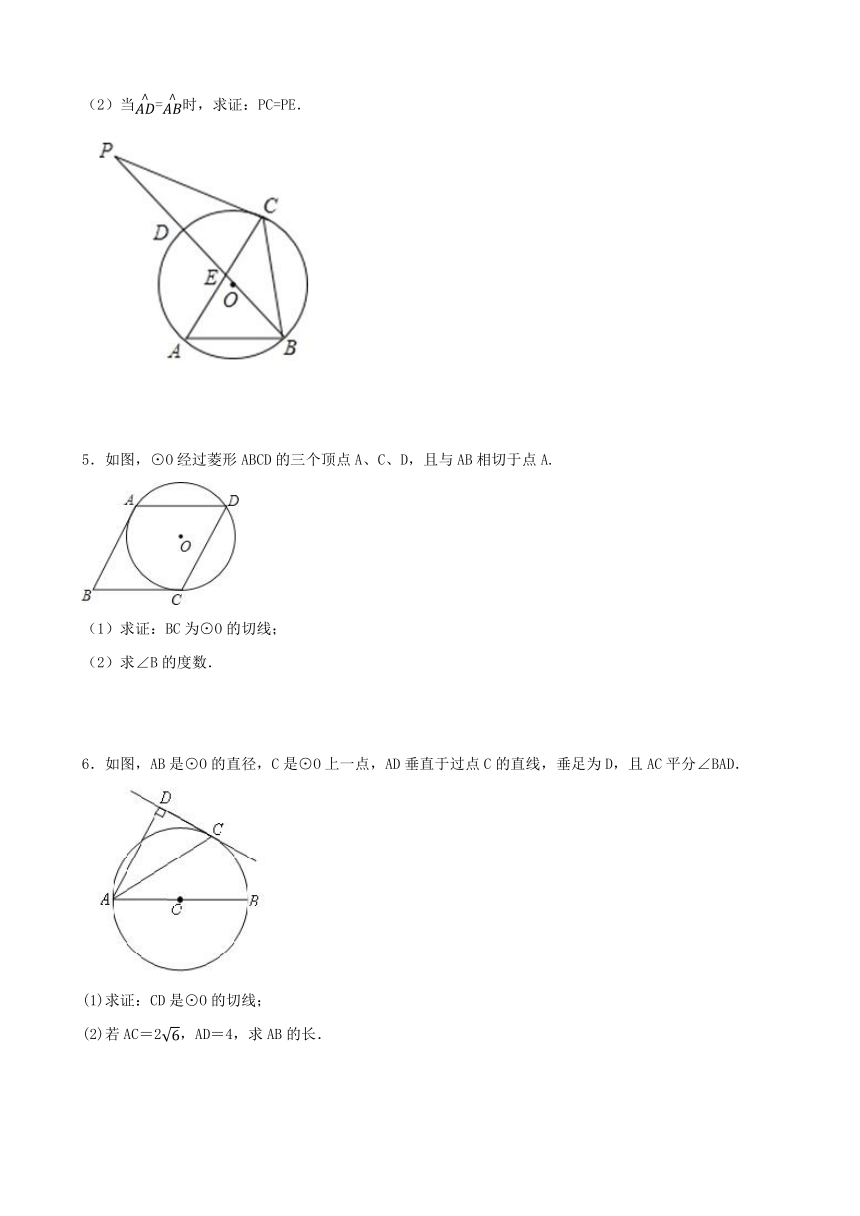
4.如图,在锐角△ABC中,∠A=60°,⊙O是△ABC的外接圆,射线BO交AC于E点.交⊙O于D点,P是射线BD上一点,且CP=CB.
(1)求证:PC是⊙O的切线;
(2)当=时,求证:PC=PE.
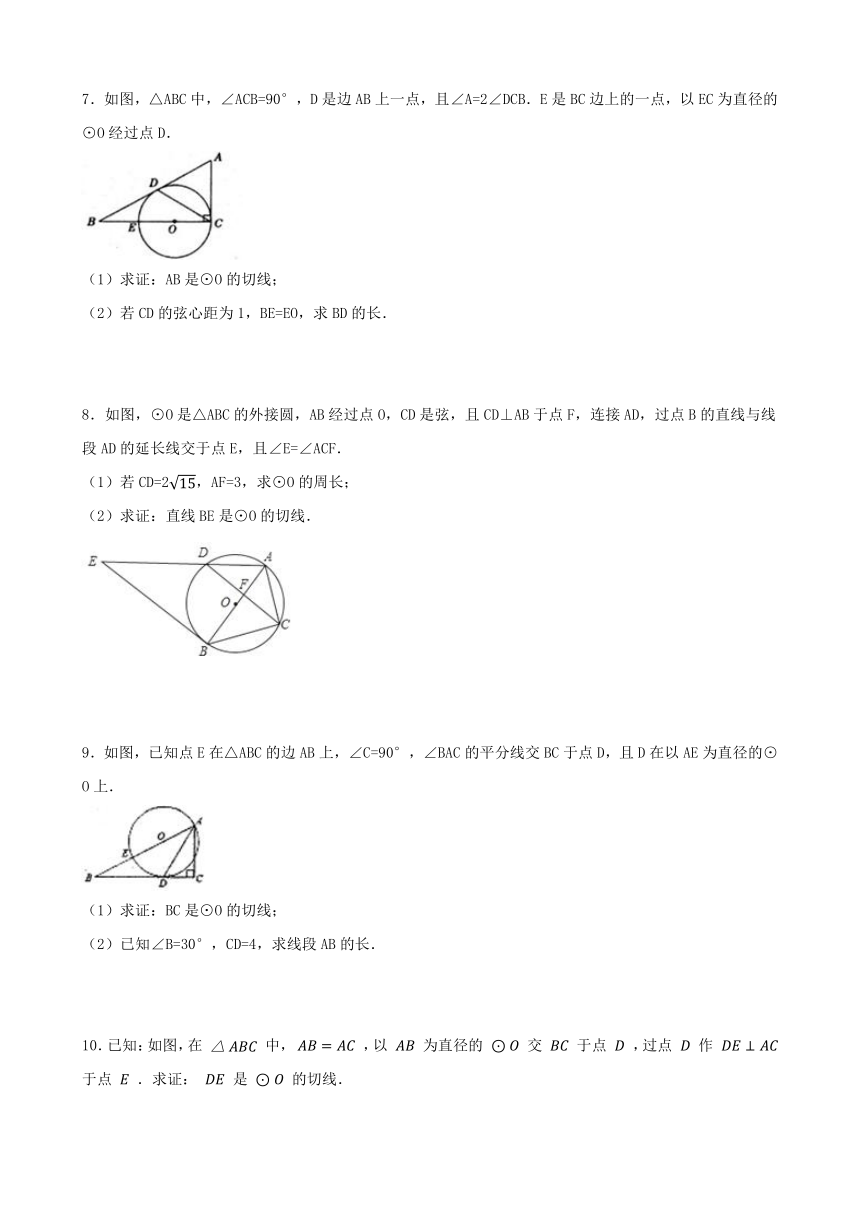
5.如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A.
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
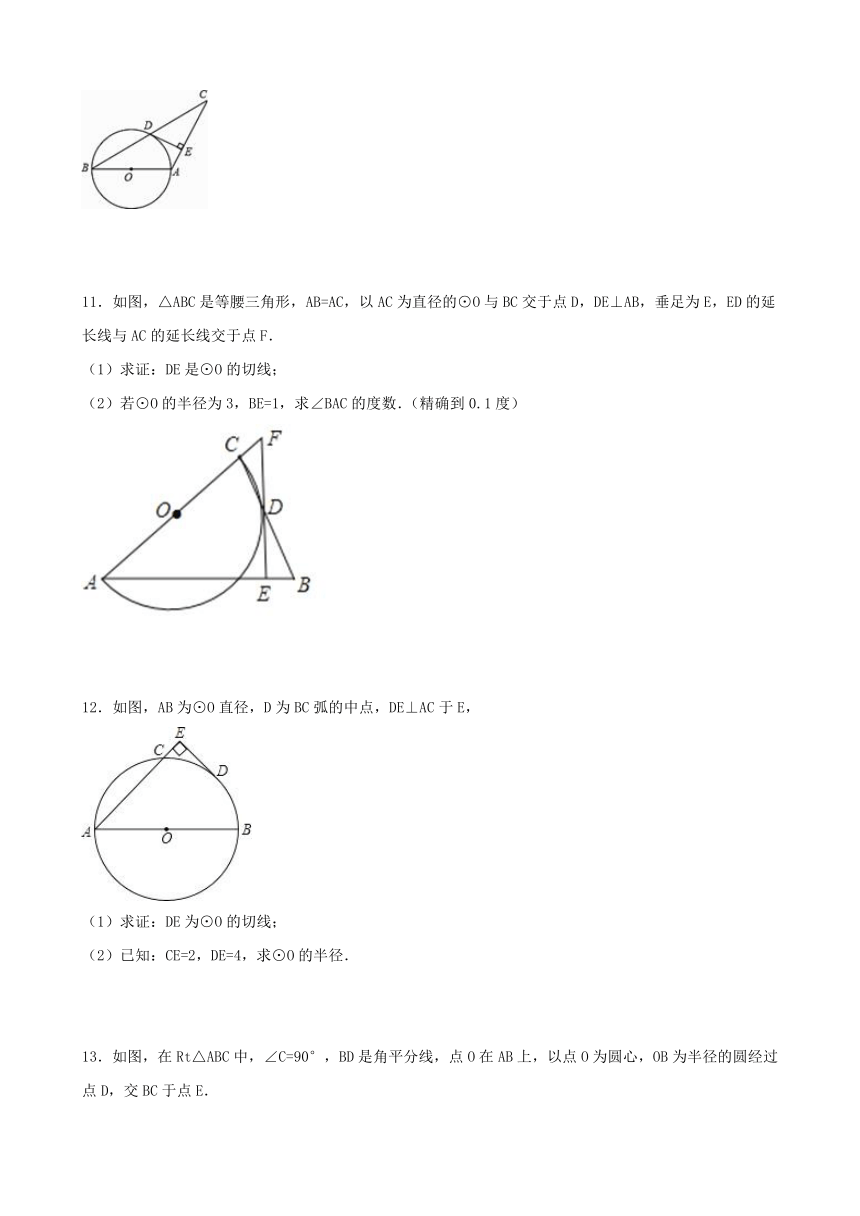
6.如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
(2)若AC=2,AD=4,求AB的长.
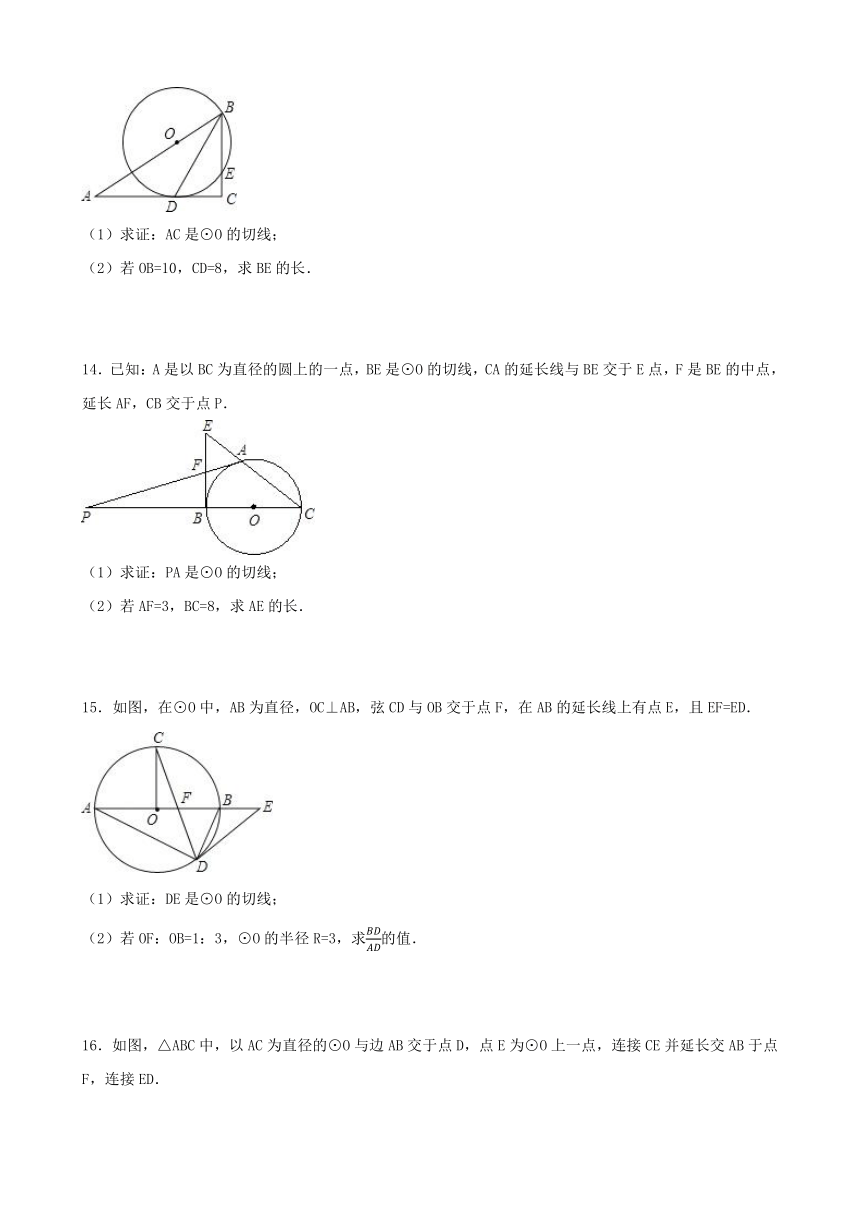
7.如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
8.如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2,AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
9.如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.
10.已知:如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 .求证: 是 的切线.
11.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为3,BE=1,求∠BAC的度数.(精确到0.1度)
12.如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,
(1)求证:DE为⊙O的切线;
(2)已知:CE=2,DE=4,求⊙O的半径.
13.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
14.已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P.
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
15.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求的值.
16.如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
17.如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
18.如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
答案
1.证明:连接OC,
∵OA=OB,CA=CB,
∴△OAB是等腰三角形,
又OC是底边AB上的中线,
∴OC⊥AB,
∴AB是⊙O的切线.
2.解:连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠BAF,
∴∠OAE=∠DAE,
∴∠OEA=∠EAD,
∴OE∥AD,
∵ED⊥AF,
∴OE⊥DE,
∴CD是⊙O的切线.
3.解:(1)连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH=4,
∴CE=4.
4.(1)证明:连接CO,
∵∠A=60°
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∵CP=CB,
∴∠CPB=∠CBP=30°,
∵∠BOC=120°,
∴∠DOC=60°,
∴∠PCO=90°,
∴PC是⊙O的切线;
(2)连接CD,
∵BD是⊙O的直径,
∴∠BCD=90°,
∵=,
∴∠ACB=∠ACD=45°,
∵PC是⊙O的切线,
∴∠PCD=∠PBC=30°,
∴∠PCE=∠ACD+∠PCD=75°,
∵∠P=30°,
∴∠PEC=75°,
∴∠PEC=∠PCE=75°,
∴PC=PE.
5.解:(1)连结OA、OB、OC、BD,如图,
∵AB与⊙O切于A点,
∴OA⊥AB,即∠OAB=90°,
∵四边形ABCD为菱形,
∴BA=BC,
在△ABO和△CBO中
∴△ABO≌△CBO(SSS),
∴∠BCO=∠BAO=90°,
∴OC⊥BC,
∴BC为⊙O的切线;
(2)∵△ABO≌△CBO,
∴∠AOB=∠COB,
∵四边形ABCD为菱形,
∴BD平分∠ABC,DA=DC,
∴点O在BD上,
∵∠BOC=∠ODC+∠OCD,OD=OC,
∴∠ODC=∠OCD,
∴∠BOC=2∠ODC,
同理:∠BOC=2∠OBC,
∵∠BOC+∠OBC=90°,
∴∠OBC=30°,
∴∠ABC=2∠OBC=60°.
6.(1)证明:连结OC
∵OA=OC,∴∠1=∠2
∵AC平分∠BAD,∴∠1=∠3.
∴∠2=∠3.
∴OC//AD
∴∠OCE=∠ADC
∵AD⊥DC∴∠ADC=90°
∴∠OCE=90°
∴CD是⊙O的切线.
(2)解:连结BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
又∵∠ADC=90°,∠1=∠3,
∴cos∠1=cos∠3,
即,∴AB=
把AC=2,AD=4代入,得:AB=6.
7.解;(1)证明:连接OD,如图1所示:
∵OD=OC,
∴∠DCB=∠ODC,
又∠DOB为△COD的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
又∵∠A=2∠DCB,
∴∠A=∠DOB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠DOB+∠B=90°,
∴∠BDO=90°,
∴OD⊥AB,
又∵D在⊙O上,
∴AB是⊙O的切线;
(2)解法一:
过点O作OM⊥CD于点M,如图1,
∵OD=OE=BE=BO,∠BDO=90°,
∴∠B=30°,
∴∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC,
又∵∠DOB为△ODC的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
∴∠DCB=30°,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∴OD=2,BO=BE+OE=2OE=4,
∴在Rt△BDO中,根据勾股定理得:BD=;
解法二:
过点O作OM⊥CD于点M,连接DE,如图2,
∵OM⊥CD,
∴CM=DM,又O为EC的中点,
∴OM为△DCE的中位线,且OM=1,
∴DE=2OM=2,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∵Rt△BDO中,OE=BE,
∴DE=BO,
∴BO=BE+OE=2OE=4,
∴OD=OE=2,
在Rt△BDO中,根据勾股定理得BD=.
8.解:(1)连接OC.设半径为r,
∵OA⊥CD,
∴DF=FC=,
在Rt△OFC中,∵∠OFC=90°,FC=,OF=r﹣3,OC=r,
∴r2=(r﹣3)2+()2,
∴r=4,
∴⊙O的周长为8π.
(2)证明:∵OA⊥CD,
∴DF=FC,AD=AC,∠AFD=90°
∴∠ADC=∠ACD,
∵∠E=∠ACD,
∴∠ADC=∠E,
∴CD∥EB,
∴∠AFD=∠ABE=90°,
∴BE是⊙O的切线.
9.解:(1)证明:连结OD,如图,
∵∠BAC的平分线交BC于点D,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)∵∠B=30°,
∴∠BAC=60°,
∴∠CAD=30°,
在Rt△ADC中,DC=4,
∴AC=DC=4,
在Rt△ABC中,∠B=30°,
∴AB=2AC=8.
10.解:连接OD.∵OD=OB,∴∠B=∠ODB.∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.
11.(1)证明:连结AD、OD,如图,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:∵AB=AC=6,AD垂直平分BC,
∴∠BAD=∠CAD,
∵∠DAE=∠BAD,
∴Rt△ADE∽Rt△ABD,
∴AD:AB=AE:AD,即AD:6=5:AD,
∴AD=,
在Rt△ADE中,∵cos∠DAE===,
∴∠DAE≈23.4°,
∴∠BAC=46.8°.
12.(1)证明:连接OD、BC交于点F,如图所示:
∵D为弧BC的中点,
∴OD⊥BC,
∵AB为直径,
∴∠ACB=90°,
又∵DE⊥AC,
∴∠CED=∠ECF=∠CFD=90°,
∴∠FDE=90°,即OD⊥DE,
又∵OD为⊙O的半径,
∴DE是⊙O的切线
(2)解:∵OD⊥BC,
∴BF=CF,
∵∠CED=∠ECF=∠CFD=90°,
∴四边形DECF是矩形,
∴CE=DF=2,CF=DE=4,
设⊙O的半径为r,则OF=r﹣2,
在Rt△OBF中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径为5.
13.(1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线
(2)解:过O作OG⊥BC,连接OE,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12.
14.(1)证明:连接AB,OA,OF;
∵F是BE的中点,
∴FE=BF.
∵OB=OC,
∴OF∥EC.
∴∠C=∠POF.
∴∠AOF=∠CAO.
∵∠C=∠CAO,
∴∠POF=∠AOF.
∵BO=AO,OF=OF,
∴∠OAP=∠EBC=90°.
∴PA是⊙O的切线
(2)解:∵BE是⊙O的切线,PA是⊙O的切线,
∴BF=AF=3,
∴BE=6.
∵BC=8,∠CBE=90°,
∴CE=10.
∵BE是⊙O的切线,
∴EB2=AE EC.
∴AE=3.6.
15.(1)证明:连结OD,如图,
∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED=∠DAE,
∴△EBD∽△EDA,
∴,即==,
∴x=2,
∴==.
16.(1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC=180°,
∴∠FED=∠A,
∵∠B+∠FED=90°,
∴∠B+∠A=90°,
∴∠BCA=90°,
∴BC是⊙O的切线;
(2)解:∵∠CFA=∠DFE,∠FED=∠A,
∴△FED∽△FAC,
∴,
∴=,
解得:AC=9,即⊙O的直径为9.
17.(1)证明:连接BD,如图1所示:
∵AB是⊙O的直径
∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD
∵∠ABC=2∠CAF,
∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线
(2)解:连接AE,如图2所示:
∵AB是⊙O的直径
∴∠AEB=90°,即△AEB为直角三角形,
∵CE:EB=1:3,
设CE长为x,则EB长为3x,BC长为4x.
则AB长为4x,
在Rt△AEB中由勾股定理可得 AE= ,
在Rt△AEC中,AC=4,AE= ,CE=x,
由勾股定理得: ,
解得: ,
∵x>0
∴ ,即CE长为 .
18.(1)证明:如图,连接OE.
∵CD是圆O的直径,
∴∠CED=90°.
∵OC=OE,
∴∠1=∠2.
又∵∠PED=∠C,即∠PED=∠1,
∴∠PED=∠2,
∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,
∴OE⊥EP,
又∵点E在圆上,
∴PE是⊙O的切线;
(2)证明:∵AB、CD为⊙O的直径,
∴∠AEB=∠CED=90°,
∴∠3=∠4(同角的余角相等).
又∵∠PED=∠1,
∴∠PED=∠4,
即ED平分∠BEP;
(3)解:设EF=x,则CF=2x,
∵⊙O的半径为5,
∴OF=2x﹣5,
在Rt△OEF中,OE2=OF2+EF2,即52=x2+(2x﹣5)2,
解得x=4,
∴EF=4,
∴BE=2EF=8,CF=2EF=8,
∴DF=CD﹣CF=10﹣8=2,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AB=10,BE=8,
∴AE=6,
∵∠BEP=∠A,∠EFP=∠AEB=90°,
∴△AEB∽△EFP,
∴ = ,即 = ,
∴PF= ,
∴PD=PF﹣DF= ﹣2=
1.如图,直线AB经过⊙O上的一点C,并且OA=OB,CA=CB,求证:直线AB是⊙O的切线.
2.如图,AB是的直径,点F在上,∠BAF的平分线AE交于点E,过点E作,交AF的延长线于点D,延长DE、AB相交于点C.求证:CD是的切线;
3.在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.
4.如图,在锐角△ABC中,∠A=60°,⊙O是△ABC的外接圆,射线BO交AC于E点.交⊙O于D点,P是射线BD上一点,且CP=CB.
(1)求证:PC是⊙O的切线;
(2)当=时,求证:PC=PE.
5.如图,⊙O经过菱形ABCD的三个顶点A、C、D,且与AB相切于点A.
(1)求证:BC为⊙O的切线;
(2)求∠B的度数.
6.如图,AB是⊙O的直径,C是⊙O上一点,AD垂直于过点C的直线,垂足为D,且AC平分∠BAD.
(1)求证:CD是⊙O的切线;
(2)若AC=2,AD=4,求AB的长.
7.如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
8.如图,⊙O是△ABC的外接圆,AB经过点O,CD是弦,且CD⊥AB于点F,连接AD,过点B的直线与线段AD的延长线交于点E,且∠E=∠ACF.
(1)若CD=2,AF=3,求⊙O的周长;
(2)求证:直线BE是⊙O的切线.
9.如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
(1)求证:BC是⊙O的切线;
(2)已知∠B=30°,CD=4,求线段AB的长.
10.已知:如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 .求证: 是 的切线.
11.如图,△ABC是等腰三角形,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为3,BE=1,求∠BAC的度数.(精确到0.1度)
12.如图,AB为⊙O直径,D为BC弧的中点,DE⊥AC于E,
(1)求证:DE为⊙O的切线;
(2)已知:CE=2,DE=4,求⊙O的半径.
13.如图,在Rt△ABC中,∠C=90°,BD是角平分线,点O在AB上,以点O为圆心,OB为半径的圆经过点D,交BC于点E.
(1)求证:AC是⊙O的切线;
(2)若OB=10,CD=8,求BE的长.
14.已知:A是以BC为直径的圆上的一点,BE是⊙O的切线,CA的延长线与BE交于E点,F是BE的中点,延长AF,CB交于点P.
(1)求证:PA是⊙O的切线;
(2)若AF=3,BC=8,求AE的长.
15.如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有点E,且EF=ED.
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求的值.
16.如图,△ABC中,以AC为直径的⊙O与边AB交于点D,点E为⊙O上一点,连接CE并延长交AB于点F,连接ED.
(1)若∠B+∠FED=90°,求证:BC是⊙O的切线;
(2)若FC=6,DE=3,FD=2,求⊙O的直径.
17.如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
18.如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
答案
1.证明:连接OC,
∵OA=OB,CA=CB,
∴△OAB是等腰三角形,
又OC是底边AB上的中线,
∴OC⊥AB,
∴AB是⊙O的切线.
2.解:连接OE,
∵OA=OE,
∴∠OAE=∠OEA,
∵AE平分∠BAF,
∴∠OAE=∠DAE,
∴∠OEA=∠EAD,
∴OE∥AD,
∵ED⊥AF,
∴OE⊥DE,
∴CD是⊙O的切线.
3.解:(1)连接OE.
∵OE=OB,
∴∠OBE=∠OEB,
∵BE平分∠ABC,
∴∠OBE=∠EBC,
∴∠EBC=∠OEB,
∴OE∥BC,
∴∠OEA=∠C,
∵∠ACB=90°,
∴∠OEA=90°
∴AC是⊙O的切线;
(2)连接OE、OF,过点O作OH⊥BF交BF于H,
由题意可知四边形OECH为矩形,
∴OH=CE,
∵BF=6,
∴BH=3,
在Rt△BHO中,OB=5,
∴OH=4,
∴CE=4.
4.(1)证明:连接CO,
∵∠A=60°
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∵CP=CB,
∴∠CPB=∠CBP=30°,
∵∠BOC=120°,
∴∠DOC=60°,
∴∠PCO=90°,
∴PC是⊙O的切线;
(2)连接CD,
∵BD是⊙O的直径,
∴∠BCD=90°,
∵=,
∴∠ACB=∠ACD=45°,
∵PC是⊙O的切线,
∴∠PCD=∠PBC=30°,
∴∠PCE=∠ACD+∠PCD=75°,
∵∠P=30°,
∴∠PEC=75°,
∴∠PEC=∠PCE=75°,
∴PC=PE.
5.解:(1)连结OA、OB、OC、BD,如图,
∵AB与⊙O切于A点,
∴OA⊥AB,即∠OAB=90°,
∵四边形ABCD为菱形,
∴BA=BC,
在△ABO和△CBO中
∴△ABO≌△CBO(SSS),
∴∠BCO=∠BAO=90°,
∴OC⊥BC,
∴BC为⊙O的切线;
(2)∵△ABO≌△CBO,
∴∠AOB=∠COB,
∵四边形ABCD为菱形,
∴BD平分∠ABC,DA=DC,
∴点O在BD上,
∵∠BOC=∠ODC+∠OCD,OD=OC,
∴∠ODC=∠OCD,
∴∠BOC=2∠ODC,
同理:∠BOC=2∠OBC,
∵∠BOC+∠OBC=90°,
∴∠OBC=30°,
∴∠ABC=2∠OBC=60°.
6.(1)证明:连结OC
∵OA=OC,∴∠1=∠2
∵AC平分∠BAD,∴∠1=∠3.
∴∠2=∠3.
∴OC//AD
∴∠OCE=∠ADC
∵AD⊥DC∴∠ADC=90°
∴∠OCE=90°
∴CD是⊙O的切线.
(2)解:连结BC.
∵AB是⊙O的直径,
∴∠ACB=90°.
又∵∠ADC=90°,∠1=∠3,
∴cos∠1=cos∠3,
即,∴AB=
把AC=2,AD=4代入,得:AB=6.
7.解;(1)证明:连接OD,如图1所示:
∵OD=OC,
∴∠DCB=∠ODC,
又∠DOB为△COD的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
又∵∠A=2∠DCB,
∴∠A=∠DOB,
∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠DOB+∠B=90°,
∴∠BDO=90°,
∴OD⊥AB,
又∵D在⊙O上,
∴AB是⊙O的切线;
(2)解法一:
过点O作OM⊥CD于点M,如图1,
∵OD=OE=BE=BO,∠BDO=90°,
∴∠B=30°,
∴∠DOB=60°,
∵OD=OC,
∴∠DCB=∠ODC,
又∵∠DOB为△ODC的外角,
∴∠DOB=∠DCB+∠ODC=2∠DCB,
∴∠DCB=30°,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∴OD=2,BO=BE+OE=2OE=4,
∴在Rt△BDO中,根据勾股定理得:BD=;
解法二:
过点O作OM⊥CD于点M,连接DE,如图2,
∵OM⊥CD,
∴CM=DM,又O为EC的中点,
∴OM为△DCE的中位线,且OM=1,
∴DE=2OM=2,
∵在Rt△OCM中,∠DCB=30°,OM=1,
∴OC=2OM=2,
∵Rt△BDO中,OE=BE,
∴DE=BO,
∴BO=BE+OE=2OE=4,
∴OD=OE=2,
在Rt△BDO中,根据勾股定理得BD=.
8.解:(1)连接OC.设半径为r,
∵OA⊥CD,
∴DF=FC=,
在Rt△OFC中,∵∠OFC=90°,FC=,OF=r﹣3,OC=r,
∴r2=(r﹣3)2+()2,
∴r=4,
∴⊙O的周长为8π.
(2)证明:∵OA⊥CD,
∴DF=FC,AD=AC,∠AFD=90°
∴∠ADC=∠ACD,
∵∠E=∠ACD,
∴∠ADC=∠E,
∴CD∥EB,
∴∠AFD=∠ABE=90°,
∴BE是⊙O的切线.
9.解:(1)证明:连结OD,如图,
∵∠BAC的平分线交BC于点D,
∴∠BAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵∠C=90°,
∴∠ODB=90°,
∴OD⊥BC,
∴BC是⊙O的切线;
(2)∵∠B=30°,
∴∠BAC=60°,
∴∠CAD=30°,
在Rt△ADC中,DC=4,
∴AC=DC=4,
在Rt△ABC中,∠B=30°,
∴AB=2AC=8.
10.解:连接OD.∵OD=OB,∴∠B=∠ODB.∵AB=AC,∴∠B=∠C,∴∠C=∠ODB,∴OD∥AC,∴∠ODE=∠DEC;∵DE⊥AC,∴∠DEC=90°,∴∠ODE=90°,即DE⊥OD,∴DE是⊙O的切线.
11.(1)证明:连结AD、OD,如图,
∵AC为⊙O的直径,
∴∠ADC=90°,
∴AD⊥BC,
∵AB=AC,
∴BD=CD,
而OA=OC,
∴OD为△ABC的中位线,
∴OD∥AB,
∵DE⊥AB,
∴DE⊥OD,
∴DE是⊙O的切线;
(2)解:∵AB=AC=6,AD垂直平分BC,
∴∠BAD=∠CAD,
∵∠DAE=∠BAD,
∴Rt△ADE∽Rt△ABD,
∴AD:AB=AE:AD,即AD:6=5:AD,
∴AD=,
在Rt△ADE中,∵cos∠DAE===,
∴∠DAE≈23.4°,
∴∠BAC=46.8°.
12.(1)证明:连接OD、BC交于点F,如图所示:
∵D为弧BC的中点,
∴OD⊥BC,
∵AB为直径,
∴∠ACB=90°,
又∵DE⊥AC,
∴∠CED=∠ECF=∠CFD=90°,
∴∠FDE=90°,即OD⊥DE,
又∵OD为⊙O的半径,
∴DE是⊙O的切线
(2)解:∵OD⊥BC,
∴BF=CF,
∵∠CED=∠ECF=∠CFD=90°,
∴四边形DECF是矩形,
∴CE=DF=2,CF=DE=4,
设⊙O的半径为r,则OF=r﹣2,
在Rt△OBF中,由勾股定理得:(r﹣2)2+42=r2,
解得:r=5,
即⊙O的半径为5.
13.(1)证明:连接OD,
∵BD为∠ABC平分线,
∴∠1=∠2,
∵OB=OD,
∴∠1=∠3,
∴∠2=∠3,
∴OD∥BC,
∵∠C=90°,
∴∠ODA=90°,
则AC为圆O的切线
(2)解:过O作OG⊥BC,连接OE,
∴四边形ODCG为矩形,
∴GC=OD=OB=10,OG=CD=8,
在Rt△OBG中,利用勾股定理得:BG=6,
∵OG⊥BE,OB=OE,
∴BE=2BG=12.
解得:BE=12.
14.(1)证明:连接AB,OA,OF;
∵F是BE的中点,
∴FE=BF.
∵OB=OC,
∴OF∥EC.
∴∠C=∠POF.
∴∠AOF=∠CAO.
∵∠C=∠CAO,
∴∠POF=∠AOF.
∵BO=AO,OF=OF,
∴∠OAP=∠EBC=90°.
∴PA是⊙O的切线
(2)解:∵BE是⊙O的切线,PA是⊙O的切线,
∴BF=AF=3,
∴BE=6.
∵BC=8,∠CBE=90°,
∴CE=10.
∵BE是⊙O的切线,
∴EB2=AE EC.
∴AE=3.6.
15.(1)证明:连结OD,如图,
∵EF=ED,
∴∠EFD=∠EDF,
∵∠EFD=∠CFO,
∴∠CFO=∠EDF,
∵OC⊥OF,
∴∠OCF+∠CFO=90°,
而OC=OD,
∴∠OCF=∠ODF,
∴∠ODC+∠EDF=90°,即∠ODE=90°,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OF:OB=1:3,
∴OF=1,BF=2,
设BE=x,则DE=EF=x+2,
∵AB为直径,
∴∠ADB=90°,
∴∠ADO=∠BDE,
而∠ADO=∠A,
∴∠BDE=∠A,
而∠BED=∠DAE,
∴△EBD∽△EDA,
∴,即==,
∴x=2,
∴==.
16.(1)证明:∵∠A+∠DEC=180°,∠FED+∠DEC=180°,
∴∠FED=∠A,
∵∠B+∠FED=90°,
∴∠B+∠A=90°,
∴∠BCA=90°,
∴BC是⊙O的切线;
(2)解:∵∠CFA=∠DFE,∠FED=∠A,
∴△FED∽△FAC,
∴,
∴=,
解得:AC=9,即⊙O的直径为9.
17.(1)证明:连接BD,如图1所示:
∵AB是⊙O的直径
∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD
∵∠ABC=2∠CAF,
∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线
(2)解:连接AE,如图2所示:
∵AB是⊙O的直径
∴∠AEB=90°,即△AEB为直角三角形,
∵CE:EB=1:3,
设CE长为x,则EB长为3x,BC长为4x.
则AB长为4x,
在Rt△AEB中由勾股定理可得 AE= ,
在Rt△AEC中,AC=4,AE= ,CE=x,
由勾股定理得: ,
解得: ,
∵x>0
∴ ,即CE长为 .
18.(1)证明:如图,连接OE.
∵CD是圆O的直径,
∴∠CED=90°.
∵OC=OE,
∴∠1=∠2.
又∵∠PED=∠C,即∠PED=∠1,
∴∠PED=∠2,
∴∠PED+∠OED=∠2+∠OED=90°,即∠OEP=90°,
∴OE⊥EP,
又∵点E在圆上,
∴PE是⊙O的切线;
(2)证明:∵AB、CD为⊙O的直径,
∴∠AEB=∠CED=90°,
∴∠3=∠4(同角的余角相等).
又∵∠PED=∠1,
∴∠PED=∠4,
即ED平分∠BEP;
(3)解:设EF=x,则CF=2x,
∵⊙O的半径为5,
∴OF=2x﹣5,
在Rt△OEF中,OE2=OF2+EF2,即52=x2+(2x﹣5)2,
解得x=4,
∴EF=4,
∴BE=2EF=8,CF=2EF=8,
∴DF=CD﹣CF=10﹣8=2,
∵AB为⊙O的直径,
∴∠AEB=90°,
∵AB=10,BE=8,
∴AE=6,
∵∠BEP=∠A,∠EFP=∠AEB=90°,
∴△AEB∽△EFP,
∴ = ,即 = ,
∴PF= ,
∴PD=PF﹣DF= ﹣2=
同课章节目录
