人教版八年级上册数学《第十二章 全等三角形》综合检测卷(含解析)
文档属性
| 名称 | 人教版八年级上册数学《第十二章 全等三角形》综合检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 580.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 22:01:11 | ||
图片预览


文档简介
八年级上册数学《第十二章 全等三角形》综合检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为( )
A.50° B.60° C.70° D.80°
2.(3分)如图,已知△ABC≌△CDA,并且BC=AD,则下列结论中错误的是( )
A.∠1=∠2 B.AB=CD C.∠B=∠D D.AC=DC
3.(3分)如图,点E是△ABC的边AC的中点,过点C作CF∥AB,连接FE并延长,交AB于点D,若AB=9,CF=6,则BD的长为( )
A.2 B.2.5 C.3 D.4.5
4.(3分)如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.0 B.1 C.2 D.3
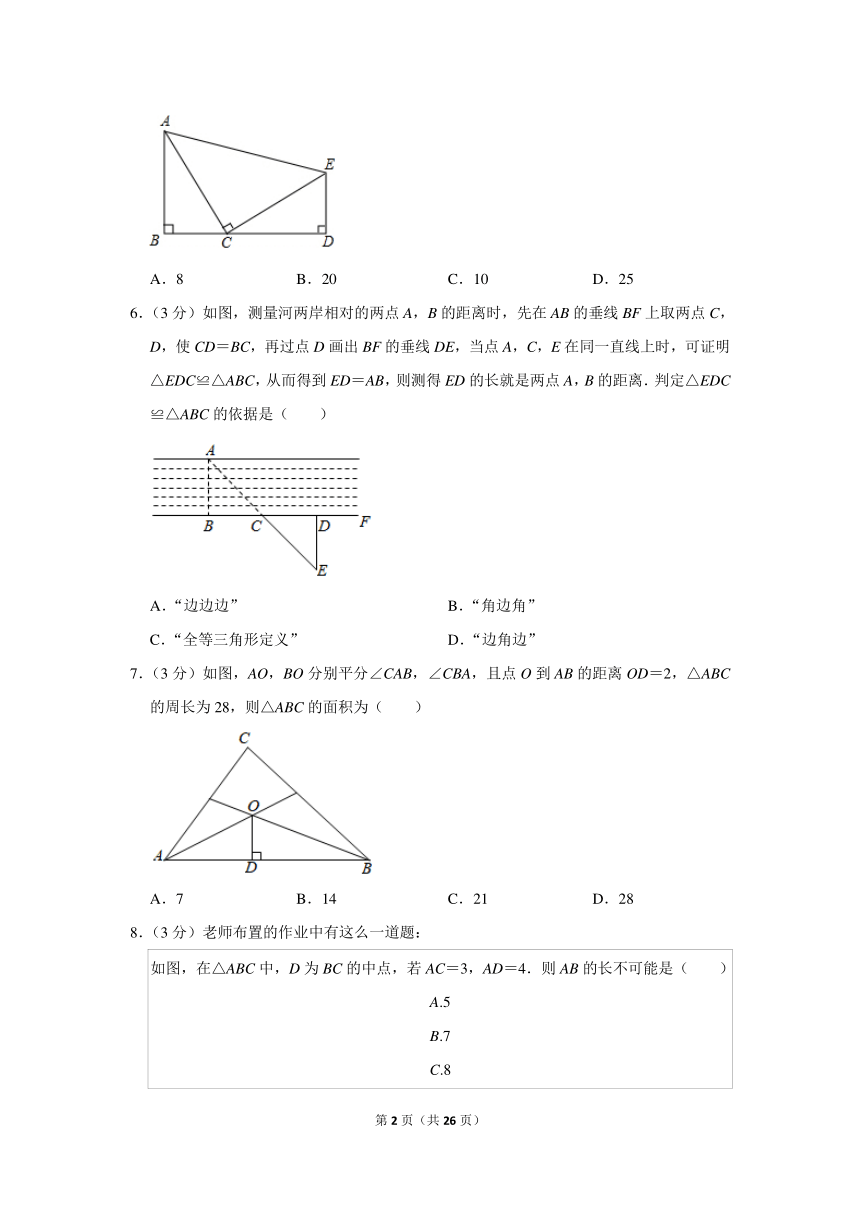
5.(3分)如图,∠B=∠D=90°,AC=EC,AB=4,ED=2,点C在线段BD上.若∠ACE=90°,则△ACE的面积是( )
A.8 B.20 C.10 D.25
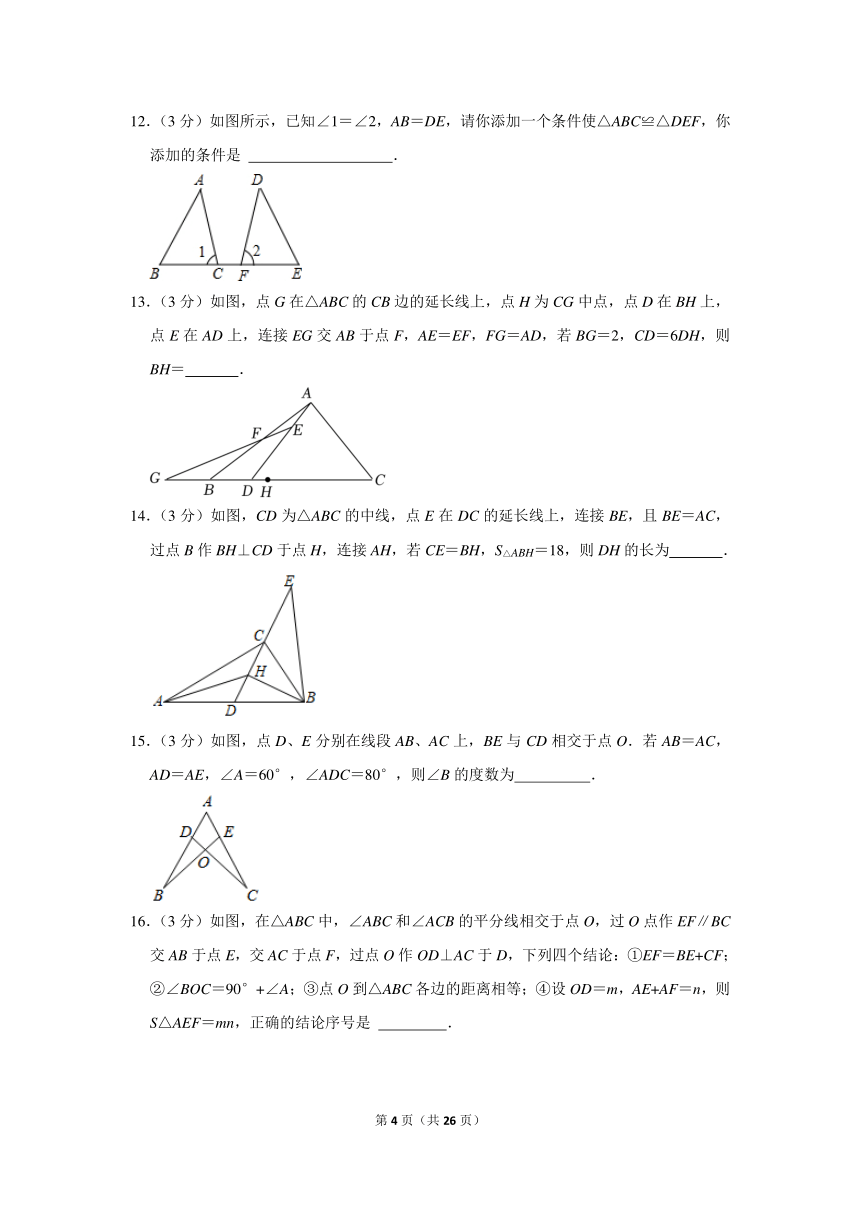
6.(3分)如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( )
A.“边边边” B.“角边角”
C.“全等三角形定义” D.“边角边”
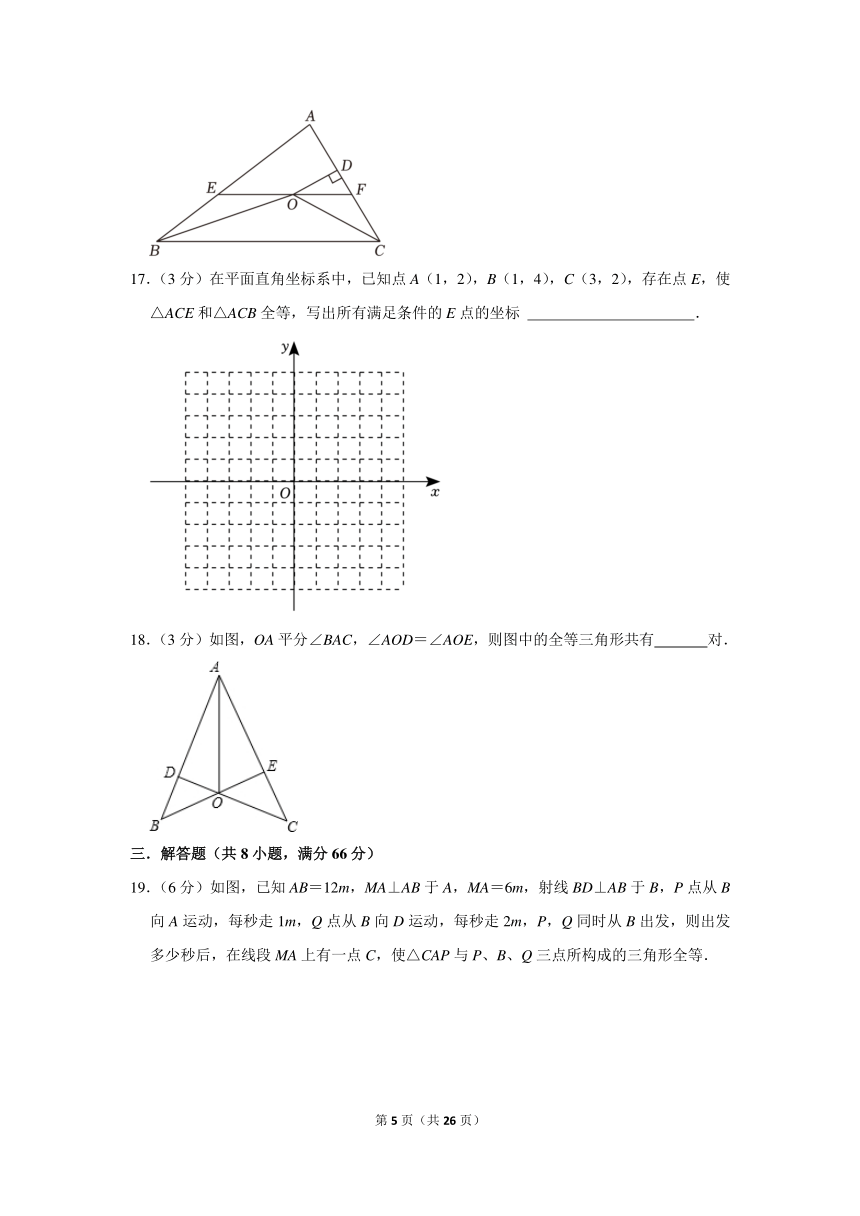
7.(3分)如图,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2,△ABC的周长为28,则△ABC的面积为( )
A.7 B.14 C.21 D.28
8.(3分)老师布置的作业中有这么一道题:
如图,在△ABC中,D为BC的中点,若AC=3,AD=4.则AB的长不可能是( )A.5B.7C.8D.9
甲同学认为AB,AC,AD这条三边不在同一个三角形中,无法解答,老师给的题目有错误.乙同学认为可以从中点D出发,构造辅助线,利用全等的知识解决.丙同学认为没必要借助全等三角形的知识,只需构造一个特殊四边形,就可以解决关于三位同学的思考过程,你认为正确的是( )
A.甲 B.乙 C.丙 D.乙和丙
9.(3分)如图,已知AB+AC=18,点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC于D.若OD=3,则四边形ABOC的面积是( )
A.36 B.27 C.20 D.18
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE、BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)已知△ABC≌△DEF,△ABC的周长为50,DE=15,DF=13,则BC= .
12.(3分)如图所示,已知∠1=∠2,AB=DE,请你添加一个条件使△ABC≌△DEF,你添加的条件是 .
13.(3分)如图,点G在△ABC的CB边的延长线上,点H为CG中点,点D在BH上,点E在AD上,连接EG交AB于点F,AE=EF,FG=AD,若BG=2,CD=6DH,则BH= .
14.(3分)如图,CD为△ABC的中线,点E在DC的延长线上,连接BE,且BE=AC,过点B作BH⊥CD于点H,连接AH,若CE=BH,S△ABH=18,则DH的长为 .
15.(3分)如图,点D、E分别在线段AB、AC上,BE与CD相交于点O.若AB=AC,AD=AE,∠A=60°,∠ADC=80°,则∠B的度数为 .
16.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论序号是 .
17.(3分)在平面直角坐标系中,已知点A(1,2),B(1,4),C(3,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .
18.(3分)如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有 对.
三.解答题(共8小题,满分66分)
19.(6分)如图,已知AB=12m,MA⊥AB于A,MA=6m,射线BD⊥AB于B,P点从B向A运动,每秒走1m,Q点从B向D运动,每秒走2m,P,Q同时从B出发,则出发多少秒后,在线段MA上有一点C,使△CAP与P、B、Q三点所构成的三角形全等.
20.(7分)如图,△ABC内一点P,AB=AC,∠BAC=36°,∠PBA=30°,∠PCA=18°,求证:AP=BC.
21.(8分)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.(1)求证:EF=BE+FD;
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?
22.(8分)如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD相交于点O,用所学公理、定理、定义证明:
(1)△ABC≌△ADC;
(2)OB=OD.
23.(8分)如图,在△ABC中,∠A=60°,D为AB上一点,连接CD.
(1)如图1,若∠ACB=90°,CD⊥AB,AC=2,则BD= ;
(2)如图2,作DF∥AC,且DF=AC=BD,连接BF,CF,求证:△ABF≌△BAC.
24.(8分)如图,已知A、B、C、D四点顺次在同一条直线上,AE∥FD,AE=FD,AB=CD,求证:∠ACE=∠DBF.
25.(9分)把两个同样大小的含30°角的三角尺按照如图1所示方式叠合放置,得到如图2的Rt△ABC和Rt△ABD,设M是AD与BC的交点,则这时MC的长度就等于点M到AB的距离,你知道这是为什么吗?请说明理由.
26.(12分)如图1,直线l交x轴、y轴分别于A、B两点,A(a,0),B(0,b),且(a﹣b)2+|b﹣4|=0.
(1)求A、B两点坐标;
(2)如图2,C为线段AB上一点,且C点的横坐标是3.求△AOC的面积;
(3)如图2,在(2)的条件下,以OC为直角边作等腰直角△POC,请求出P点坐标;
(4)如图3,在(2)的条件下,过B点作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
八年级上册数学《第十二章 全等三角形》综合检测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1. 解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=40°,
∴△ABD中,∠B=(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
故选:C.
2. 解:∵△ABC≌△CDA,
∴∠1=∠2,∠D=∠B,AB=CD.
故选:D.
3. 证明:∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6,
∵AB=9,
∴BD=AB﹣AD=9﹣6=3,
故选:C.
4. 解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
5. 解:∵∠B=∠D=90°,
∴∠BAC+∠BCA=90°,∠ECD+∠BCA=90°,
∴∠BAC=∠ECD,
在△ABC和△CDE中,,
∴△ABC≌△CDE(AAS),
∴BC=ED=2,
∴AC2=AB2+BC2=42+22=20,
∵AC=EC,
∴△ACE的面积=AC×EC=AC2=10,
故选:C.
6. 解:∵∠ACB=∠DCE,CD=BC,∠ABC=∠EDC,
∴△EDC≌△ABC(ASA),
故选:B.
7. 解:连接OC,过点O作OE⊥AC于E,OF⊥BC于F,
∵AO,BO分别平分∠CAB,∠CBA,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OF=OD=2,
∴△ABC的面积=△AOC的面积+△AOB的面积+△BOC的面积
=×AC×OE+×AB×OD+×BC×OF
=×(AB+AC+BC)×2
=28.
故选:D.
8. 解:如图所示,
延长AD到E使得AD=ED=4,
∵D是BC的中点,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵AE﹣AC<EC<AE+AC,
∴5<EC<11,即5<AB<11.
如图所示,
取AB中点F,连接DF,
∵D、F分别为BC、AB的中点,
∴DF是ABC的中位线,AB=2AF,
∴DF=AC=,
∵AD﹣DF<AF<AD+DF,
∴<AF<.
∴5<AB<11.
甲说法错误,乙和丙说法正确.
故选:D.
9. 解:
过O作OE⊥AB于E,OF⊥AC于F,连接OA,
∵点O为∠ABC与∠ACB的平分线的交点,OD⊥BC于D,OD=3,
∴OE=OD=3,OF=OD=3,
∵AB+AC=18,
∴四边形ABOC的面积S=S△ABO+S△ACO=
=
=×(AB+AC)
=×18
=27,
故选:B.
10. 解:∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB=180°﹣∠CBA﹣∠CAB=180°﹣(180°﹣∠C)=90°+∠C,故①错误;
∵∠C=60°,
∴∠BAC+∠ABC=120°,
∵AE,BF分别是∠BAC与ABC的平分线,
∴∠OAB+∠OBA=(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,
∴∠HBO=∠EBO,
在△HBO和△EBO中,
,
∴△HBO≌△EBO(SAS),
∴∠BOH=∠BOE=60°,
∴∠AOH=180°﹣60°﹣60°=60°,
∴∠AOH=∠AOF,
在△HAO和△FAO中,
,
∴△HAO≌△FAO(ASA),
∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OH=OM=OD=a,
∵AB+AC+BC=2b
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,③正确.
综上所述:正确的为:②③.
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
11. 解:如图:
∵ABC的周长为50,DE=15,DF=13,
∴EF=50﹣15﹣13=22,
∵△ABC≌△DEF,
∴EF=BC=22,
故答案为:22.
12. 解:添加的条件是∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
故答案为:∠A=∠D(答案不唯一).
13. 解:如图,作GP∥AD,交AB的延长线于点P,
∵AE=EF,∠AFE=∠PFG,
∴∠FAE=∠AFE,∠FAE=∠PFG,
∵GP∥AD,
∴∠FAE=∠FPG,∠PFG=∠FPG,
∴FG=PG,
∵FG=AD,
∴PG=AD,
在△PBG与△ABD中,
,
∴△PBG≌△ABD(AAS),
∴GB=BD,
∵BG=2,CD=6DH,点H为GC的中点,
设DH=m,CD=6m,
则GH=HC,
则2+2+m=6m﹣m,
∴m=1,即DH=1,
∴BH=BD+DH=2+1=3,
故答案为:3.
14. 解:如图,过点A作AF⊥EF于点F
∵CD为△ABC的中线,BH⊥CD
∴AD=BD,∠AFD=∠BHD=90°
又∵∠ADF=∠BDH
∴△ADF≌△BDH(AAS)
∴AF=BH,FD=HD
∵在Rt△CAF和Rt△EBH中
∴Rt△CAF≌Rt△EBH(HL)
∴EH=CF
∴EH﹣CH=CF﹣CH,即EC=HF
∵BH=EC,EC=HF=HD+DF,HD=DF
∴BH=HD+DF=2DH
∵CD为△ABC的中线,BH⊥CD
∴S△BHD=S△ABH=×18=9
又∵S△BHD=HD HB=HD×2HD
∴HD×2HD=9
解得:HD=3
故答案为:3.
15. 解:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,
∵∠A=60°,∠ADC=80°,
∴∠C=180°﹣∠ADC﹣∠A=180°﹣80°﹣60°=40°,
∴∠B=40°.
故答案为:40°.
16. 解:①∵OB是∠ABC的平分线,
∴∠EBO=∠CBO,
∵EF∥BC,
∴∠EOB=∠CBO,
∴∠EBO=∠EOB,
∴OE=BE,
同理:OF=CF,
∴EF=OE+OF=BE+CF,
故结论①正确;
②∵∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣∠A)=90°+∠A,
故结论②不正确;
③过点O作OT⊥AB于T,OH⊥BC于H,连接OA,如图所示:
∵OB是∠ABC的平分线,
∴OT=OH,
∵OC是∠ACB的平分线,OD⊥AC,
∴OH=OD,
∴OT=OH=OD,
∴点O到△ABC各边的距离相等,
故结论③正确;
④∵OD=m,AE+AF=n,
由③正确得:OT=OD=m,
∴S△AOE=AE OT=AE m,S△AOF=AF OD=AF m,
∴S△AEF=S△AOE+S△AOF=m(AE+AF)=mn.
故结论④不正确.
综上所述:正确的结论是①③.
故答案为:①③.
17. 解:如图所示:
E点坐标为(1,0),(3,0),(3,4),
故答案为:(1,0),(3,0),(3,4).
18. 解:∵OA平分∠BAC,
∴∠DAO=∠EAO.
在△DAO和△EAO中,,
∴△DAO≌△EAO(ASA).
∴OD=OE,∠ADO=∠AEO,
∴∠BDO=∠CEO.
在△BDO和△CEO中,,
∴△BDO≌△CEO(ASA),
∴OB=OC.
∵∠AOD=∠AOE,∠BOD=∠COE,
∴∠AOB=∠AOC.
在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
∴AB=AC,∠B=∠C.
在△ABE和△ACD中,,
∴△ABE≌△ACD(ASA).
故答案为:4.
三.解答题(共8小题,满分66分)
19. 解:当△APC≌△BQP时,AP=BQ,即12﹣x=2x,
解得:x=4;
当△APC≌△BPQ时,AP=BP=AB=6m,
此时所用时间为6秒,AC=BQ=12m,不合题意,舍去;
综上,出发4秒后,在线段MA上有一点C,使△CAP与P、B、Q三点所构成的三角形全等.
20. 证明:过点A作AF⊥BC,垂足为F,延长CP交AF于点Q,连BQ,BP延长线上取点D,使BQ=QD,连接AD、DC、DQ.
∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°;
又∵∠ACP=18°,
∴∠QCB=54°,
∵BQ=CQ,
∴∠QBC=54°;
在△BQC中,
∴∠BQC=72°.
又∵∠PBA=30°,
∴∠ABQ+∠QBP=30°,∠QBP+∠PBC=54°,∠ABQ+∠QBP+∠PBC=72°,
∴∠ABQ=12°,∠QBP=12°;
又∵BQ=DQ,
∴∠QDB=12°,∠BQD=156°,
∴∠DQP=∠BQD﹣BQP=84°;
在△QDP中,∠DPQ=180°﹣∠PDQ﹣∠PQD=84°,
∴DQ=DP;
在△BQA中,∠AQB=180°﹣∠QAB﹣∠QBA=144°,
∴∠AQD=360°﹣∠AQB﹣∠BQD=60°,
∴∠ADP=∠ADQ+∠QDP=72°;
又∵BQ=DQ=AQ,
∴△AQD是等边三角形,
∴AD=DQ=AQ,BQ=AD;
在△BQC和△ADP中,
∴△BQC≌△ADP(SAS),
∴BC=AP.
21. (1)证明:延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.
∴∠GAE=∠EAF.
又∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(2)(1)中的结论EF=BE+FD,仍然成立,
证明:如图2,延长CB至M,使BM=DF,
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF=∠BAD,
∴∠2+∠4=∠BAD=∠EAF.
∴∠3+∠4=∠EAF,即∠MAE=∠EAF.
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME,即EF=BE+BM,
∴EF=BE+DF.
22. 证明:(1)在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠CAB=∠CAD,
在△BAO和△DAO中,
,
∴△BAO≌△DAO(SAS),
∴OB=OD.
23. (1)解:∵CD⊥AB,∠BAC=60°,
∴∠ACD=30°,
∴,
∵∠ACB=90°,
∴∠B=30°,
∴AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3,
故答案为:3;
(2)证明:∵DF∥AC,
∴∠BDF=∠BAC=60°,
又∵DF=BD,
∴△BDF为等边三角形,
∴∠DBF=∠BAC=60°,BF=DF,
即BF=AC,
在△ABF和△BAC中,
,
∴△ABF≌△BAC(SAS).
24. 解:证明:∵AE∥DF,
∴∠A=∠D.
∵AB=CD,
∴AB+BC=CD+BC.
即AC=BD.
在△AEC和△DFB中,
,
∴△AEC≌△DFB(SAS),
∴∠ACE=∠DBF.
25. 解:过M点作MH⊥AB于H,如图,
∵∠BAD=30°,∠BAC=60°,
∴∠CAM=∠BAC﹣∠BAD=60°﹣30°=30°,
∴AM平分∠BAC,
∵MC⊥AC,MH⊥AB,
∴MH=MC,
即MC的长度就等于点M到AB的距离.
26. 解:(1)∵(a﹣b)2+|b﹣4|=0,
∴,解得
∴A(4,0),B(0,4);
(2)如图1,过C作CD⊥x轴于D.
∵xC=3,A(4,0),B(0,4)
∴OD=3,OA=OB=4,
∴AD=OA﹣OD=1,∠BAO=45°,
∴CD=AD=1,
∴S△AOC=OA CD=2,即△AOC的面积为2;
(3)如图1,当∠POC=90°时,过P作PE⊥x轴于E,
则∠PEO=∠CDO=90°,
∴∠EPO+∠EOP=90°.
∵△POC是等腰直角三角形,
∴OP=OC,∠POC=90°.
∴∠EOP+∠COD=90°.
∴∠EPO=∠COD.
在△EPO和△DOC中,
,
∴△EPO≌△DOC(AAS),
∴OE=CD=1,PE=OD=3,
∴P(﹣1,3);
如图2,当∠PCO=90°且P在C的下方时,过C作CM⊥y轴于M,过P作PN⊥MC于N,
同理证得△COM≌△PCN(AAS),
∴PN=CM=3,CN=OM=1,
∴MN=3+1=4,
∴P(4,﹣2),
当∠PCO=90°且P在C的下方时,同理证得P(1,5);
综上,P点的坐标为(1,﹣3)或(1,5)或(4,﹣2);
(4)OD=AE.理由如下:
如图3,过A作AG⊥x轴于A,交OC延长线于G.
∴∠GAO=90°.
∵OB⊥OA,BD⊥OC,
∴∠BOD=∠BFO=90°,
∴∠OBD+∠BOF=∠AOF+∠BOF=90°.
∴∠OBD=∠AOF.
在△BOD和△OAG中,
,
∴△BOD≌△OAG(ASA)
∴∠BDO=∠G,OD=AG.
∵∠CEA=∠BDO,
∴∠CEA=∠G.
∵∠BAO=45°,∠GAO=90°,
∴∠BAO=∠CAG=45°.
在△CEA和△CGA中,
,
∴△CEA≌△CGA(AAS),
∴AE=AG,
∴OD=AE.
第1页(共1页)
一.选择题(共10小题,满分30分,每小题3分)
1.(3分)如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠ADE的度数为( )
A.50° B.60° C.70° D.80°
2.(3分)如图,已知△ABC≌△CDA,并且BC=AD,则下列结论中错误的是( )
A.∠1=∠2 B.AB=CD C.∠B=∠D D.AC=DC
3.(3分)如图,点E是△ABC的边AC的中点,过点C作CF∥AB,连接FE并延长,交AB于点D,若AB=9,CF=6,则BD的长为( )
A.2 B.2.5 C.3 D.4.5
4.(3分)如图,∠C=∠D=90°,添加下列条件:①AC=AD;②∠ABC=∠ABD;③BC=BD,其中能判定Rt△ABC与Rt△ABD全等的条件的个数是( )
A.0 B.1 C.2 D.3
5.(3分)如图,∠B=∠D=90°,AC=EC,AB=4,ED=2,点C在线段BD上.若∠ACE=90°,则△ACE的面积是( )
A.8 B.20 C.10 D.25
6.(3分)如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( )
A.“边边边” B.“角边角”
C.“全等三角形定义” D.“边角边”
7.(3分)如图,AO,BO分别平分∠CAB,∠CBA,且点O到AB的距离OD=2,△ABC的周长为28,则△ABC的面积为( )
A.7 B.14 C.21 D.28
8.(3分)老师布置的作业中有这么一道题:
如图,在△ABC中,D为BC的中点,若AC=3,AD=4.则AB的长不可能是( )A.5B.7C.8D.9
甲同学认为AB,AC,AD这条三边不在同一个三角形中,无法解答,老师给的题目有错误.乙同学认为可以从中点D出发,构造辅助线,利用全等的知识解决.丙同学认为没必要借助全等三角形的知识,只需构造一个特殊四边形,就可以解决关于三位同学的思考过程,你认为正确的是( )
A.甲 B.乙 C.丙 D.乙和丙
9.(3分)如图,已知AB+AC=18,点O为∠ABC与∠ACB的平分线的交点,且OD⊥BC于D.若OD=3,则四边形ABOC的面积是( )
A.36 B.27 C.20 D.18
10.(3分)如图,在△ABC中,∠BAC和∠ABC的平分线AE、BF相交于点O,AE交BC于E,BF交AC于F,过点O作OD⊥BC于D,下列四个结论:①∠AOB=90°+∠C;②当∠C=60°时,AF+BE=AB;③若OD=a,AB+BC+CA=2b,则S△ABC=ab.其中正确的是( )
A.①② B.②③ C.①②③ D.①③
二.填空题(共8小题,满分24分,每小题3分)
11.(3分)已知△ABC≌△DEF,△ABC的周长为50,DE=15,DF=13,则BC= .
12.(3分)如图所示,已知∠1=∠2,AB=DE,请你添加一个条件使△ABC≌△DEF,你添加的条件是 .
13.(3分)如图,点G在△ABC的CB边的延长线上,点H为CG中点,点D在BH上,点E在AD上,连接EG交AB于点F,AE=EF,FG=AD,若BG=2,CD=6DH,则BH= .
14.(3分)如图,CD为△ABC的中线,点E在DC的延长线上,连接BE,且BE=AC,过点B作BH⊥CD于点H,连接AH,若CE=BH,S△ABH=18,则DH的长为 .
15.(3分)如图,点D、E分别在线段AB、AC上,BE与CD相交于点O.若AB=AC,AD=AE,∠A=60°,∠ADC=80°,则∠B的度数为 .
16.(3分)如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论序号是 .
17.(3分)在平面直角坐标系中,已知点A(1,2),B(1,4),C(3,2),存在点E,使△ACE和△ACB全等,写出所有满足条件的E点的坐标 .
18.(3分)如图,OA平分∠BAC,∠AOD=∠AOE,则图中的全等三角形共有 对.
三.解答题(共8小题,满分66分)
19.(6分)如图,已知AB=12m,MA⊥AB于A,MA=6m,射线BD⊥AB于B,P点从B向A运动,每秒走1m,Q点从B向D运动,每秒走2m,P,Q同时从B出发,则出发多少秒后,在线段MA上有一点C,使△CAP与P、B、Q三点所构成的三角形全等.
20.(7分)如图,△ABC内一点P,AB=AC,∠BAC=36°,∠PBA=30°,∠PCA=18°,求证:AP=BC.
21.(8分)(1)如图1,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD.(1)求证:EF=BE+FD;
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?
22.(8分)如图,在四边形ABCD中,AB=AD,BC=DC,AC,BD相交于点O,用所学公理、定理、定义证明:
(1)△ABC≌△ADC;
(2)OB=OD.
23.(8分)如图,在△ABC中,∠A=60°,D为AB上一点,连接CD.
(1)如图1,若∠ACB=90°,CD⊥AB,AC=2,则BD= ;
(2)如图2,作DF∥AC,且DF=AC=BD,连接BF,CF,求证:△ABF≌△BAC.
24.(8分)如图,已知A、B、C、D四点顺次在同一条直线上,AE∥FD,AE=FD,AB=CD,求证:∠ACE=∠DBF.
25.(9分)把两个同样大小的含30°角的三角尺按照如图1所示方式叠合放置,得到如图2的Rt△ABC和Rt△ABD,设M是AD与BC的交点,则这时MC的长度就等于点M到AB的距离,你知道这是为什么吗?请说明理由.
26.(12分)如图1,直线l交x轴、y轴分别于A、B两点,A(a,0),B(0,b),且(a﹣b)2+|b﹣4|=0.
(1)求A、B两点坐标;
(2)如图2,C为线段AB上一点,且C点的横坐标是3.求△AOC的面积;
(3)如图2,在(2)的条件下,以OC为直角边作等腰直角△POC,请求出P点坐标;
(4)如图3,在(2)的条件下,过B点作BD⊥OC,交OC、OA分别于F、D两点,E为OA上一点,且∠CEA=∠BDO,试判断线段OD与AE的数量关系,并说明理由.
八年级上册数学《第十二章 全等三角形》综合检测卷
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1. 解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,AB=AD,∠ADE=∠B,
∴∠EAC=∠DAB=40°,
∴△ABD中,∠B=(180°﹣∠BAD)=70°,
∴∠ADE=∠B=70°,
故选:C.
2. 解:∵△ABC≌△CDA,
∴∠1=∠2,∠D=∠B,AB=CD.
故选:D.
3. 证明:∵CF∥AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE=CE,
在△ADE和△CFE中,
,
∴△ADE≌△CFE(AAS),
∴AD=CF=6,
∵AB=9,
∴BD=AB﹣AD=9﹣6=3,
故选:C.
4. 解:①当AC=AD时,由∠C=∠D=90°,AC=AD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
②当∠ABC=∠ABD时,由∠C=∠D=90°,∠ABC=∠ABD且AB=AB,可得Rt△ABC≌Rt△ABD(AAS);
③当BC=BD时,由∠C=∠D=90°,BC=BD且AB=AB,可得Rt△ABC≌Rt△ABD(HL);
故选:D.
5. 解:∵∠B=∠D=90°,
∴∠BAC+∠BCA=90°,∠ECD+∠BCA=90°,
∴∠BAC=∠ECD,
在△ABC和△CDE中,,
∴△ABC≌△CDE(AAS),
∴BC=ED=2,
∴AC2=AB2+BC2=42+22=20,
∵AC=EC,
∴△ACE的面积=AC×EC=AC2=10,
故选:C.
6. 解:∵∠ACB=∠DCE,CD=BC,∠ABC=∠EDC,
∴△EDC≌△ABC(ASA),
故选:B.
7. 解:连接OC,过点O作OE⊥AC于E,OF⊥BC于F,
∵AO,BO分别平分∠CAB,∠CBA,OD⊥AB,OE⊥AC,OF⊥BC,
∴OE=OF=OD=2,
∴△ABC的面积=△AOC的面积+△AOB的面积+△BOC的面积
=×AC×OE+×AB×OD+×BC×OF
=×(AB+AC+BC)×2
=28.
故选:D.
8. 解:如图所示,
延长AD到E使得AD=ED=4,
∵D是BC的中点,
∴BD=CD,
在△ABD和△ECD中,
,
∴△ABD≌△ECD(SAS),
∴AB=EC,
∵AE﹣AC<EC<AE+AC,
∴5<EC<11,即5<AB<11.
如图所示,
取AB中点F,连接DF,
∵D、F分别为BC、AB的中点,
∴DF是ABC的中位线,AB=2AF,
∴DF=AC=,
∵AD﹣DF<AF<AD+DF,
∴<AF<.
∴5<AB<11.
甲说法错误,乙和丙说法正确.
故选:D.
9. 解:
过O作OE⊥AB于E,OF⊥AC于F,连接OA,
∵点O为∠ABC与∠ACB的平分线的交点,OD⊥BC于D,OD=3,
∴OE=OD=3,OF=OD=3,
∵AB+AC=18,
∴四边形ABOC的面积S=S△ABO+S△ACO=
=
=×(AB+AC)
=×18
=27,
故选:B.
10. 解:∵∠BAC和∠ABC的平分线相交于点O,
∴∠OBA=∠CBA,∠OAB=∠CAB,
∴∠AOB=180°﹣∠OBA﹣∠OAB=180°﹣∠CBA﹣∠CAB=180°﹣(180°﹣∠C)=90°+∠C,故①错误;
∵∠C=60°,
∴∠BAC+∠ABC=120°,
∵AE,BF分别是∠BAC与ABC的平分线,
∴∠OAB+∠OBA=(∠BAC+∠ABC)=60°,
∴∠AOB=120°,
∴∠AOF=60°,
∴∠BOE=60°,
如图,在AB上取一点H,使BH=BE,
∵BF是∠ABC的角平分线,
∴∠HBO=∠EBO,
在△HBO和△EBO中,
,
∴△HBO≌△EBO(SAS),
∴∠BOH=∠BOE=60°,
∴∠AOH=180°﹣60°﹣60°=60°,
∴∠AOH=∠AOF,
在△HAO和△FAO中,
,
∴△HAO≌△FAO(ASA),
∴AF=AH,
∴AB=BH+AH=BE+AF,故②正确;
作OH⊥AC于H,OM⊥AB于M,
∵∠BAC和∠ABC的平分线相交于点O,
∴点O在∠C的平分线上,
∴OH=OM=OD=a,
∵AB+AC+BC=2b
∴S△ABC=×AB×OM+×AC×OH+×BC×OD=(AB+AC+BC) a=ab,③正确.
综上所述:正确的为:②③.
故选:B.
二.填空题(共8小题,满分24分,每小题3分)
11. 解:如图:
∵ABC的周长为50,DE=15,DF=13,
∴EF=50﹣15﹣13=22,
∵△ABC≌△DEF,
∴EF=BC=22,
故答案为:22.
12. 解:添加的条件是∠A=∠D,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
故答案为:∠A=∠D(答案不唯一).
13. 解:如图,作GP∥AD,交AB的延长线于点P,
∵AE=EF,∠AFE=∠PFG,
∴∠FAE=∠AFE,∠FAE=∠PFG,
∵GP∥AD,
∴∠FAE=∠FPG,∠PFG=∠FPG,
∴FG=PG,
∵FG=AD,
∴PG=AD,
在△PBG与△ABD中,
,
∴△PBG≌△ABD(AAS),
∴GB=BD,
∵BG=2,CD=6DH,点H为GC的中点,
设DH=m,CD=6m,
则GH=HC,
则2+2+m=6m﹣m,
∴m=1,即DH=1,
∴BH=BD+DH=2+1=3,
故答案为:3.
14. 解:如图,过点A作AF⊥EF于点F
∵CD为△ABC的中线,BH⊥CD
∴AD=BD,∠AFD=∠BHD=90°
又∵∠ADF=∠BDH
∴△ADF≌△BDH(AAS)
∴AF=BH,FD=HD
∵在Rt△CAF和Rt△EBH中
∴Rt△CAF≌Rt△EBH(HL)
∴EH=CF
∴EH﹣CH=CF﹣CH,即EC=HF
∵BH=EC,EC=HF=HD+DF,HD=DF
∴BH=HD+DF=2DH
∵CD为△ABC的中线,BH⊥CD
∴S△BHD=S△ABH=×18=9
又∵S△BHD=HD HB=HD×2HD
∴HD×2HD=9
解得:HD=3
故答案为:3.
15. 解:在△ABE和△ACD中,
∴△ABE≌△ACD(SAS),
∴∠B=∠C,
∵∠A=60°,∠ADC=80°,
∴∠C=180°﹣∠ADC﹣∠A=180°﹣80°﹣60°=40°,
∴∠B=40°.
故答案为:40°.
16. 解:①∵OB是∠ABC的平分线,
∴∠EBO=∠CBO,
∵EF∥BC,
∴∠EOB=∠CBO,
∴∠EBO=∠EOB,
∴OE=BE,
同理:OF=CF,
∴EF=OE+OF=BE+CF,
故结论①正确;
②∵∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,
∴∠OBC+∠OCB=(∠ABC+∠ACB),
∵∠ABC+∠ACB=180°﹣∠A,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣∠A)=90°+∠A,
故结论②不正确;
③过点O作OT⊥AB于T,OH⊥BC于H,连接OA,如图所示:
∵OB是∠ABC的平分线,
∴OT=OH,
∵OC是∠ACB的平分线,OD⊥AC,
∴OH=OD,
∴OT=OH=OD,
∴点O到△ABC各边的距离相等,
故结论③正确;
④∵OD=m,AE+AF=n,
由③正确得:OT=OD=m,
∴S△AOE=AE OT=AE m,S△AOF=AF OD=AF m,
∴S△AEF=S△AOE+S△AOF=m(AE+AF)=mn.
故结论④不正确.
综上所述:正确的结论是①③.
故答案为:①③.
17. 解:如图所示:
E点坐标为(1,0),(3,0),(3,4),
故答案为:(1,0),(3,0),(3,4).
18. 解:∵OA平分∠BAC,
∴∠DAO=∠EAO.
在△DAO和△EAO中,,
∴△DAO≌△EAO(ASA).
∴OD=OE,∠ADO=∠AEO,
∴∠BDO=∠CEO.
在△BDO和△CEO中,,
∴△BDO≌△CEO(ASA),
∴OB=OC.
∵∠AOD=∠AOE,∠BOD=∠COE,
∴∠AOB=∠AOC.
在△AOB和△AOC中,,
∴△AOB≌△AOC(SAS).
∴AB=AC,∠B=∠C.
在△ABE和△ACD中,,
∴△ABE≌△ACD(ASA).
故答案为:4.
三.解答题(共8小题,满分66分)
19. 解:当△APC≌△BQP时,AP=BQ,即12﹣x=2x,
解得:x=4;
当△APC≌△BPQ时,AP=BP=AB=6m,
此时所用时间为6秒,AC=BQ=12m,不合题意,舍去;
综上,出发4秒后,在线段MA上有一点C,使△CAP与P、B、Q三点所构成的三角形全等.
20. 证明:过点A作AF⊥BC,垂足为F,延长CP交AF于点Q,连BQ,BP延长线上取点D,使BQ=QD,连接AD、DC、DQ.
∵∠A=36°,AB=AC,
∴∠ABC=∠ACB=72°;
又∵∠ACP=18°,
∴∠QCB=54°,
∵BQ=CQ,
∴∠QBC=54°;
在△BQC中,
∴∠BQC=72°.
又∵∠PBA=30°,
∴∠ABQ+∠QBP=30°,∠QBP+∠PBC=54°,∠ABQ+∠QBP+∠PBC=72°,
∴∠ABQ=12°,∠QBP=12°;
又∵BQ=DQ,
∴∠QDB=12°,∠BQD=156°,
∴∠DQP=∠BQD﹣BQP=84°;
在△QDP中,∠DPQ=180°﹣∠PDQ﹣∠PQD=84°,
∴DQ=DP;
在△BQA中,∠AQB=180°﹣∠QAB﹣∠QBA=144°,
∴∠AQD=360°﹣∠AQB﹣∠BQD=60°,
∴∠ADP=∠ADQ+∠QDP=72°;
又∵BQ=DQ=AQ,
∴△AQD是等边三角形,
∴AD=DQ=AQ,BQ=AD;
在△BQC和△ADP中,
∴△BQC≌△ADP(SAS),
∴BC=AP.
21. (1)证明:延长EB到G,使BG=DF,连接AG.
∵∠ABG=∠ABC=∠D=90°,AB=AD,
∴△ABG≌△ADF.
∴AG=AF,∠1=∠2.
∴∠1+∠3=∠2+∠3=∠EAF=∠BAD.
∴∠GAE=∠EAF.
又∵AE=AE,
∴△AEG≌△AEF.
∴EG=EF.
∵EG=BE+BG.
∴EF=BE+FD;
(2)(1)中的结论EF=BE+FD,仍然成立,
证明:如图2,延长CB至M,使BM=DF,
∵∠ABC+∠D=180°,∠1+∠ABC=180°,
∴∠1=∠D,
在△ABM与△ADF中,
∴△ABM≌△ADF(SAS).
∴AF=AM,∠2=∠3.
∵∠EAF=∠BAD,
∴∠2+∠4=∠BAD=∠EAF.
∴∠3+∠4=∠EAF,即∠MAE=∠EAF.
在△AME与△AFE中,
,
∴△AME≌△AFE(SAS).
∴EF=ME,即EF=BE+BM,
∴EF=BE+DF.
22. 证明:(1)在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS);
(2)∵△ABC≌△ADC,
∴∠CAB=∠CAD,
在△BAO和△DAO中,
,
∴△BAO≌△DAO(SAS),
∴OB=OD.
23. (1)解:∵CD⊥AB,∠BAC=60°,
∴∠ACD=30°,
∴,
∵∠ACB=90°,
∴∠B=30°,
∴AB=2AC=4,
∴BD=AB﹣AD=4﹣1=3,
故答案为:3;
(2)证明:∵DF∥AC,
∴∠BDF=∠BAC=60°,
又∵DF=BD,
∴△BDF为等边三角形,
∴∠DBF=∠BAC=60°,BF=DF,
即BF=AC,
在△ABF和△BAC中,
,
∴△ABF≌△BAC(SAS).
24. 解:证明:∵AE∥DF,
∴∠A=∠D.
∵AB=CD,
∴AB+BC=CD+BC.
即AC=BD.
在△AEC和△DFB中,
,
∴△AEC≌△DFB(SAS),
∴∠ACE=∠DBF.
25. 解:过M点作MH⊥AB于H,如图,
∵∠BAD=30°,∠BAC=60°,
∴∠CAM=∠BAC﹣∠BAD=60°﹣30°=30°,
∴AM平分∠BAC,
∵MC⊥AC,MH⊥AB,
∴MH=MC,
即MC的长度就等于点M到AB的距离.
26. 解:(1)∵(a﹣b)2+|b﹣4|=0,
∴,解得
∴A(4,0),B(0,4);
(2)如图1,过C作CD⊥x轴于D.
∵xC=3,A(4,0),B(0,4)
∴OD=3,OA=OB=4,
∴AD=OA﹣OD=1,∠BAO=45°,
∴CD=AD=1,
∴S△AOC=OA CD=2,即△AOC的面积为2;
(3)如图1,当∠POC=90°时,过P作PE⊥x轴于E,
则∠PEO=∠CDO=90°,
∴∠EPO+∠EOP=90°.
∵△POC是等腰直角三角形,
∴OP=OC,∠POC=90°.
∴∠EOP+∠COD=90°.
∴∠EPO=∠COD.
在△EPO和△DOC中,
,
∴△EPO≌△DOC(AAS),
∴OE=CD=1,PE=OD=3,
∴P(﹣1,3);
如图2,当∠PCO=90°且P在C的下方时,过C作CM⊥y轴于M,过P作PN⊥MC于N,
同理证得△COM≌△PCN(AAS),
∴PN=CM=3,CN=OM=1,
∴MN=3+1=4,
∴P(4,﹣2),
当∠PCO=90°且P在C的下方时,同理证得P(1,5);
综上,P点的坐标为(1,﹣3)或(1,5)或(4,﹣2);
(4)OD=AE.理由如下:
如图3,过A作AG⊥x轴于A,交OC延长线于G.
∴∠GAO=90°.
∵OB⊥OA,BD⊥OC,
∴∠BOD=∠BFO=90°,
∴∠OBD+∠BOF=∠AOF+∠BOF=90°.
∴∠OBD=∠AOF.
在△BOD和△OAG中,
,
∴△BOD≌△OAG(ASA)
∴∠BDO=∠G,OD=AG.
∵∠CEA=∠BDO,
∴∠CEA=∠G.
∵∠BAO=45°,∠GAO=90°,
∴∠BAO=∠CAG=45°.
在△CEA和△CGA中,
,
∴△CEA≌△CGA(AAS),
∴AE=AG,
∴OD=AE.
第1页(共1页)
