复数的概念
图片预览








文档简介
课件20张PPT。第四章 数系的扩充___复数4.1 复数的概念无实根一复习引入自然数分数有理数无理数实数①分数的引入,解决了在自然数集中不能整除的矛盾。③整数②负数的引入,解决了在正有理数集中不够减的矛盾。③无理数的引入,解决了开方开不尽的矛盾。④在实数集范围内,负数不能开平方,我们要引入什么数,才能解决这个矛盾呢?一复习引入问5:引入一个新数c? 实际上,早在16世纪时期,数学家们就已经解决了这个矛盾,而且形成了一整套完整的理论。因为这个新数不是实的数,就称为虚数单位,英文译名为imaginary number unit.所以,用“i”来表示这个新数。问6:引入的新数必须满足一定的条件,才能进行相关的运算,虚数单位i应满足什么条件呢?二新课-复数的概念问7:根据这种规定,数的范围又扩充了,会出现什么形式的数呢?二新课-复数的概念相关概念: 复数a+bi(a, b∈R)由两部分组成,实数a与b分别称为复数a+bi的实部与虚部,1与i分别是实数单位和虚数单位,
当b=0时,a+bi就是实数,
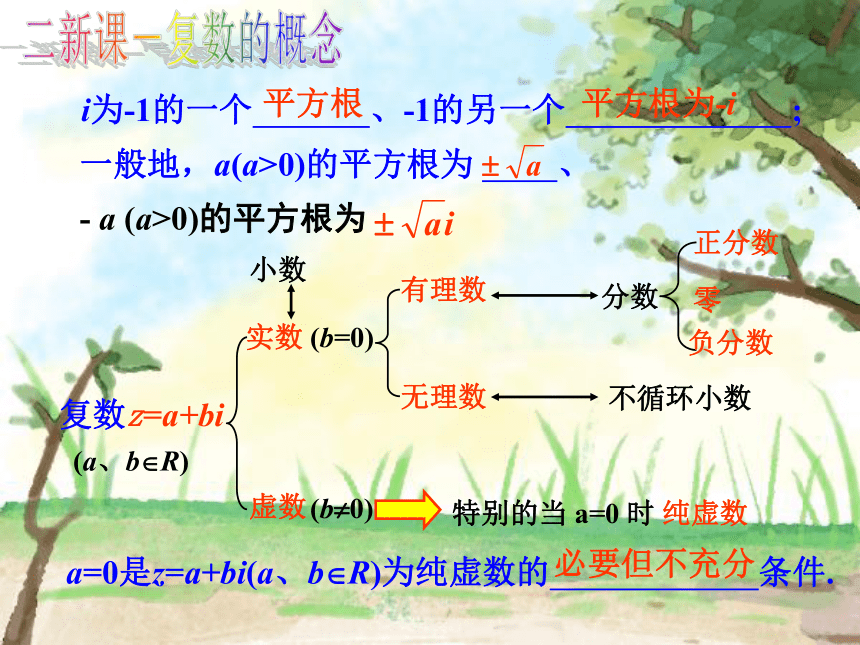
当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。 二新课-复数的概念有时把实部记成为Re(z);虚部记成为Im(z). i为-1的一个 、-1的另一个 ;一般地,a(a>0)的平方根为 、平方根平方根为-i- a (a>0)的平方根为 复数z=a+bi(a、b?R)(b=0)分数不循环小数虚数(b?0)特别的当 a=0 时纯虚数a=0是z=a+bi(a、b?R)为纯虚数的 条件. 必要但不充分二新课-复数的概念二新课-例题剖析问9:两个复数之间可以比较大小吗? 两个不全是实数的复数之间是不能比较大小的,但若它们的实部与虚部分别相等,我们就说这两个复数相等。二新课-复数的概念例2.实数 m 取什么数值时,复数z=m +1+(m-i)是:(1)实数? (2)虚数?(3)纯虚数?解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,∴ (1)m=1时,z是实数;
(2)m≠1时,z是虚数;(3)当 时,即m=-1时,z是纯虚数;二新课-例题剖析例3.已知 (2x-1) + i = y -(3-y)i ,其中 x , y ∈R,求 x 与 y .例4.已知 x2+y2-6 + (x-y-2)i =0,求实数 x 与 y 的值.二新课-例题剖析xo1实数可以用数轴上的点来表示。一一对应 规定了正方向,直线数轴原点,单位长度实数 数轴上的点 (形)(数)(几何模型)二新课-复数的概念问10:如何建立复数集与平面直角坐标系中的点集之间的联系?复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi二新课-复数的概念特别注意:虚轴不包括原点。复数的一个几何意义例5 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 表示复数的点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)一种重要的数学思想:数形结合思想二新课-例题剖析例5 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 变式:证明对一切m,此复数所对应的点不可能位于第四象限。不等式解集为空集所以复数所对应的点不可能位于第四象限.二新课-例题剖析实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。(复数的模)的几何意义:Z (a,b)二新课-复数的概念例6.设 z ∈C , 满足下列条件的点 z 的集合是什么图形?
(1)|z|=4; (2)2<|z|<4.二新课-例题剖析例7.若复数z对应点集为圆: 试求│z│的最大值与最小值.o121131二新课-例题剖析一. 数学知识:二. 数学思想:(1)复数相等(2)复平面(3)复数的模(3)类比思想(2)数形结合思想(1)转化思想三 小结
当b=0时,a+bi就是实数,
当b≠0时,a+bi是虚数,其中a=0且b≠0时称为纯虚数。 二新课-复数的概念有时把实部记成为Re(z);虚部记成为Im(z). i为-1的一个 、-1的另一个 ;一般地,a(a>0)的平方根为 、平方根平方根为-i- a (a>0)的平方根为 复数z=a+bi(a、b?R)(b=0)分数不循环小数虚数(b?0)特别的当 a=0 时纯虚数a=0是z=a+bi(a、b?R)为纯虚数的 条件. 必要但不充分二新课-复数的概念二新课-例题剖析问9:两个复数之间可以比较大小吗? 两个不全是实数的复数之间是不能比较大小的,但若它们的实部与虚部分别相等,我们就说这两个复数相等。二新课-复数的概念例2.实数 m 取什么数值时,复数z=m +1+(m-i)是:(1)实数? (2)虚数?(3)纯虚数?解:复数z=m+1+(m-1)i 中,因为m∈R,所以m+1,m-1都是实数,它们分别是z的实部和虚部,∴ (1)m=1时,z是实数;
(2)m≠1时,z是虚数;(3)当 时,即m=-1时,z是纯虚数;二新课-例题剖析例3.已知 (2x-1) + i = y -(3-y)i ,其中 x , y ∈R,求 x 与 y .例4.已知 x2+y2-6 + (x-y-2)i =0,求实数 x 与 y 的值.二新课-例题剖析xo1实数可以用数轴上的点来表示。一一对应 规定了正方向,直线数轴原点,单位长度实数 数轴上的点 (形)(数)(几何模型)二新课-复数的概念问10:如何建立复数集与平面直角坐标系中的点集之间的联系?复数z=a+bi有序实数对(a,b)直角坐标系中的点Z(a,b)xyobaZ(a,b) 建立了平面直角坐标系来表示复数的平面x轴------实轴y轴------虚轴(数)(形)------复数平面 (简称复平面)一一对应z=a+bi二新课-复数的概念特别注意:虚轴不包括原点。复数的一个几何意义例5 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 表示复数的点所在象限的问题复数的实部与虚部所满足的不等式组的问题转化(几何问题)(代数问题)一种重要的数学思想:数形结合思想二新课-例题剖析例5 已知复数z=(m2+m-6)+(m2+m-2)i在复平面内所对应的点位于第二象限,求实数m允许的取值范围。 变式:证明对一切m,此复数所对应的点不可能位于第四象限。不等式解集为空集所以复数所对应的点不可能位于第四象限.二新课-例题剖析实数绝对值的几何意义:能否把绝对值概念推广到复数范围呢?XOAa| a | = | OA | 实数a在数轴上所对应的点A到原点O的距离。xOz=a+biy| z | = |OZ|复数的绝对值 复数 z=a+bi在复平面上对应的点Z(a,b)到原点的距离。(复数的模)的几何意义:Z (a,b)二新课-复数的概念例6.设 z ∈C , 满足下列条件的点 z 的集合是什么图形?
(1)|z|=4; (2)2<|z|<4.二新课-例题剖析例7.若复数z对应点集为圆: 试求│z│的最大值与最小值.o121131二新课-例题剖析一. 数学知识:二. 数学思想:(1)复数相等(2)复平面(3)复数的模(3)类比思想(2)数形结合思想(1)转化思想三 小结
