数系的扩充
图片预览






文档简介
课件16张PPT。第四章 数系的扩充___复数4.3 数系的扩充 我们知道,对于实系数一元二次方程ax2+bx+c=0,
当b2-4ac<0时,没有实数根.这说明,人们在研究代数方程的过程中,限制实数集合,有些问题就无法解决.因此,
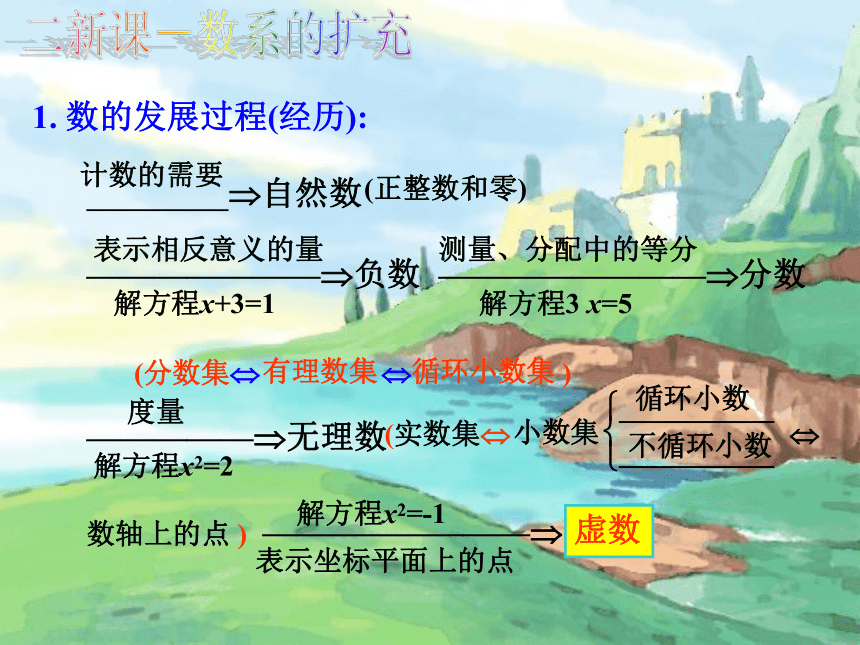
需要把实数集进一步扩充,这就是本章里我们将要学习的复数的知识. 复数是16世纪人们在解决二次方程、三次方程时引入的.大约经过了一个世纪,才逐步形成完整的理论.现在,它已在数学、力学、电学以及其他科学里得到广泛应用,是现代科学技术上普遍使用的一种数学工具. 复数的初步知识是进一步学习高等数学的基础,复数也是初等数学的基础知识.一复习引入1. 数的发展过程(经历): ?自然数 计数的需要(正整数和零) ———————?负数表示相反意义的量解方程x+3=1————————?分数测量、分配中的等分解方程3 x=5(分数集? ? )有理数集循环小数集—————?无理数度量解方程x2=2(实数集? ?小数集循环小数不循环小数数轴上的点 )解方程x2=-1表示坐标平面上的点————————?虚数二新课-数系的扩充(1) 实数集原有的有关性质和特点能否
推广到复数集?(2)从复数的特点出发,寻找复数集新
的(实数集所不具有)性质和特点?2.如何探索复数集的性质和特点?探索途径:二新课-数系的扩充3.实数集的一些性质和特点:(1) 实数可以判定相等或不相等;(2) 不相等的实数可以比较大小;(3) 实数可以用数轴上的点表示;(4) 实数可以进行四则运算;(5) 负实数不能进行开偶次方根运算;……二新课-数系的扩充4.实系数一元二次方程的根二新课-数系的扩充4.实系数一元二次方程的根在有两个虚数根的情况下,韦达定理仍然成立,即 x1+x2= ; x1x2= .二新课-数系的扩充例1:设方程x2-2x+2=0的两根为x1,x2,求x14+x24的值.解:二新课-例题剖析例2:已知方程x2+x+a=0有两虚根x1、x2,且|x1-x2|=3,求实数a.解:二新课-例题剖析解:(1)要充分运用好ω 的特点,在运算过程中发现规律.因为ω 6=1,i6=-1,所以原式=-2.二新课-例题剖析=25(-2-2i)
=-50-50i.二新课-例题剖析(2)S=1+2i+3i2+4i3+……+100i99=(1+2i+3i2+4i3)+(5i4+6i5+7i6+8i7)+
……+(97i96+98i97+99i98+100i99)=(1+2i-3-4i)+(5+6i-7-8i)+
……+(97+98i-99-100i)(A) -i(B) -i(C) -1(D) 1(C) 2.复数 在复平面上对应的点不
可能位于( )(A) 第一象限(B) 第二象限(C) 第三象限(D) 第四象限(A) 3.i 是虚数单位, ( )(A) 1 -i(B) -1-i(C) 1 +3i(D) -1 -3i(D) 二新课-练习4.(1-i)2 . i = ( )(A) 2 -2i(B) 2 +2i(C) -2(D) 2(D) 5. 设复数z满足 , 则|1+z|= ( )(A) 0(B) 1(C) (D) 2(C) 6. 已知复数z1=3+4i,z2=t+i ,且z1.z2是实数,则实数t= ( )(A)3/4 (B)4/3 (C)-4/3 (D)-3/4(A) 7. 复数z 的共轭复数是 ( )(A) (B) (C) (D)(B) 二新课-练习8. 若(a-2i)i=b-i , 其中a,b∈R,i是虚数单位,则a2+b2= ( )(A)0 (B)2 (C)5/2 (D)5(D) 9. ( ) (A)-2-i (B)-2+i (C)2-i (D)2+i(C) 10. 若复数 是纯虚数,则实数a的值
为( )(A)-2 (B)4 (C)-6 (D)6(C) 二新课-练习12.若复数z满足(3+z)i=1, 则z=_____________13.若z1=a+2i,z2=3-4i,且 为纯虚数,则实数a的值为______1-i-3-i8/3二新课-练习
当b2-4ac<0时,没有实数根.这说明,人们在研究代数方程的过程中,限制实数集合,有些问题就无法解决.因此,
需要把实数集进一步扩充,这就是本章里我们将要学习的复数的知识. 复数是16世纪人们在解决二次方程、三次方程时引入的.大约经过了一个世纪,才逐步形成完整的理论.现在,它已在数学、力学、电学以及其他科学里得到广泛应用,是现代科学技术上普遍使用的一种数学工具. 复数的初步知识是进一步学习高等数学的基础,复数也是初等数学的基础知识.一复习引入1. 数的发展过程(经历): ?自然数 计数的需要(正整数和零) ———————?负数表示相反意义的量解方程x+3=1————————?分数测量、分配中的等分解方程3 x=5(分数集? ? )有理数集循环小数集—————?无理数度量解方程x2=2(实数集? ?小数集循环小数不循环小数数轴上的点 )解方程x2=-1表示坐标平面上的点————————?虚数二新课-数系的扩充(1) 实数集原有的有关性质和特点能否
推广到复数集?(2)从复数的特点出发,寻找复数集新
的(实数集所不具有)性质和特点?2.如何探索复数集的性质和特点?探索途径:二新课-数系的扩充3.实数集的一些性质和特点:(1) 实数可以判定相等或不相等;(2) 不相等的实数可以比较大小;(3) 实数可以用数轴上的点表示;(4) 实数可以进行四则运算;(5) 负实数不能进行开偶次方根运算;……二新课-数系的扩充4.实系数一元二次方程的根二新课-数系的扩充4.实系数一元二次方程的根在有两个虚数根的情况下,韦达定理仍然成立,即 x1+x2= ; x1x2= .二新课-数系的扩充例1:设方程x2-2x+2=0的两根为x1,x2,求x14+x24的值.解:二新课-例题剖析例2:已知方程x2+x+a=0有两虚根x1、x2,且|x1-x2|=3,求实数a.解:二新课-例题剖析解:(1)要充分运用好ω 的特点,在运算过程中发现规律.因为ω 6=1,i6=-1,所以原式=-2.二新课-例题剖析=25(-2-2i)
=-50-50i.二新课-例题剖析(2)S=1+2i+3i2+4i3+……+100i99=(1+2i+3i2+4i3)+(5i4+6i5+7i6+8i7)+
……+(97i96+98i97+99i98+100i99)=(1+2i-3-4i)+(5+6i-7-8i)+
……+(97+98i-99-100i)(A) -i(B) -i(C) -1(D) 1(C) 2.复数 在复平面上对应的点不
可能位于( )(A) 第一象限(B) 第二象限(C) 第三象限(D) 第四象限(A) 3.i 是虚数单位, ( )(A) 1 -i(B) -1-i(C) 1 +3i(D) -1 -3i(D) 二新课-练习4.(1-i)2 . i = ( )(A) 2 -2i(B) 2 +2i(C) -2(D) 2(D) 5. 设复数z满足 , 则|1+z|= ( )(A) 0(B) 1(C) (D) 2(C) 6. 已知复数z1=3+4i,z2=t+i ,且z1.z2是实数,则实数t= ( )(A)3/4 (B)4/3 (C)-4/3 (D)-3/4(A) 7. 复数z 的共轭复数是 ( )(A) (B) (C) (D)(B) 二新课-练习8. 若(a-2i)i=b-i , 其中a,b∈R,i是虚数单位,则a2+b2= ( )(A)0 (B)2 (C)5/2 (D)5(D) 9. ( ) (A)-2-i (B)-2+i (C)2-i (D)2+i(C) 10. 若复数 是纯虚数,则实数a的值
为( )(A)-2 (B)4 (C)-6 (D)6(C) 二新课-练习12.若复数z满足(3+z)i=1, 则z=_____________13.若z1=a+2i,z2=3-4i,且 为纯虚数,则实数a的值为______1-i-3-i8/3二新课-练习
