七年级数学上册 3.3 代数式的值 教案 (新版)冀教版
文档属性
| 名称 | 七年级数学上册 3.3 代数式的值 教案 (新版)冀教版 |
|
|
| 格式 | zip | ||
| 文件大小 | 69.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-24 00:00:00 | ||
图片预览

文档简介
3.3 代数式的值
教学目标: 1、了解代数式的值的意义,会计算代数式的值。
2、在计算代数式的值的过程中感受数量的变化及其联系,感悟整体代入的思想。3、在探索规律的过程中感悟从具体到抽象的归纳思想方法。
教学重点:求代数式的值
教学难点:一般到特殊,具体到抽象的归纳思想
教学准备:配套课件,三角板
教学过程:
创设情境,设凝激思--------引题
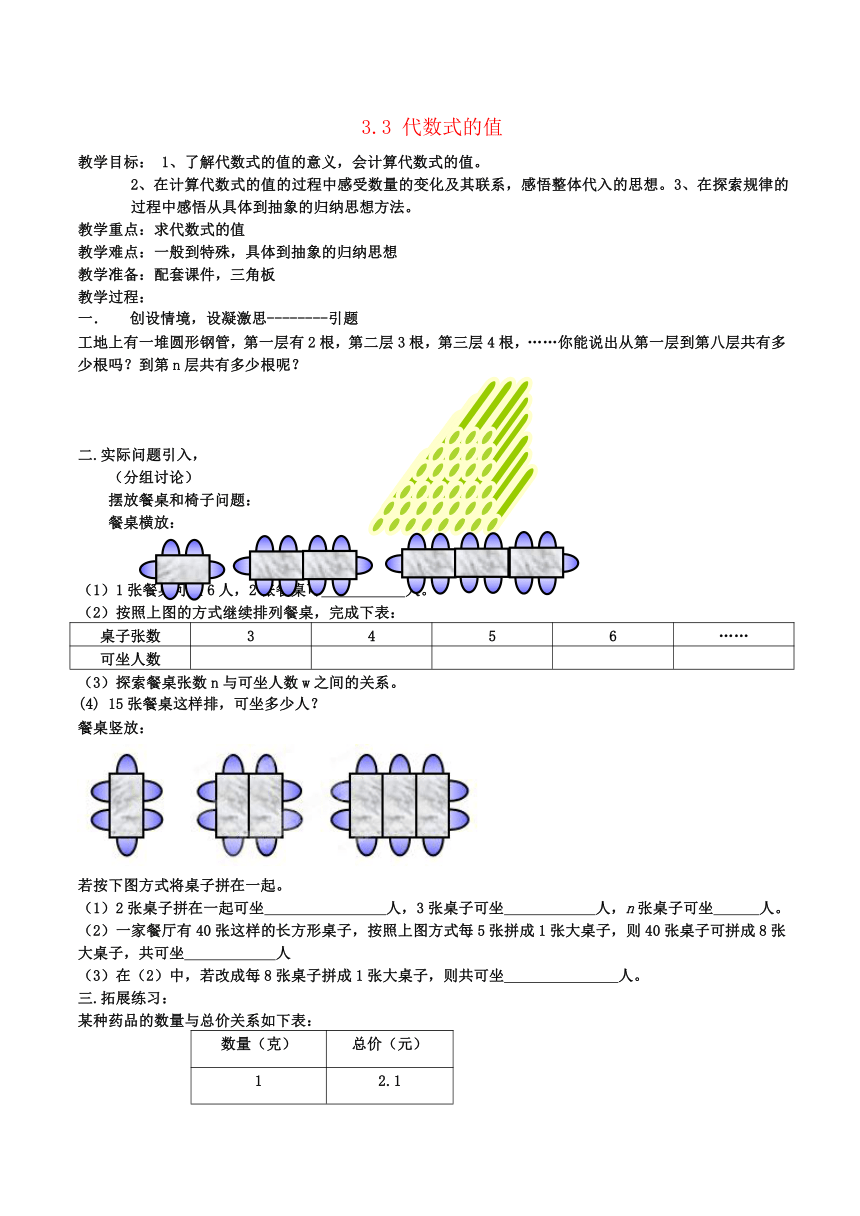
工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出从第一层到第八层共有多少根吗?到第n层共有多少根呢?
二.实际问题引入,
(分组讨论)
摆放餐桌和椅子问题:
餐桌横放:
(1)1张餐桌可坐6人,2张餐桌可 人。
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数 3 4 5 6 ……
可坐人数
(3)探索餐桌张数n与可坐人数w之间的关系。
15张餐桌这样排,可坐多少人?
餐桌竖放:
( http: / / www.21cnjy.com )
若按下图方式将桌子拼在一起。
(1)2张桌子拼在一起可坐 人,3张桌子可坐 人,n张桌子可坐 人。
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐 人。
三.拓展练习:
某种药品的数量与总价关系如下表:
数量(克) 总价(元)
1 2.1
2 4.1
3 6.1
4 8.1
…… ……
写出药品数量x(克)与总价y(元)之间的关系。
四.引申思考,发散思维
已知a+b=3,求代数式(a+b)2+a+6+b的值.
思路点拨: 本例中字母 a,b的值并不知 ( http: / / www.21cnjy.com )道,如果根据已知a+b=3来求出a,b是不可能的。观察代数式发现,其中a+b是以整体出现的,所以可将a+b直接代入原代数式求值。
解: 当 a+b=3时,
(a+b)2+a+6+b=(a+b)2 +(a +b)+6
=32+3+6
=18
误点剖析: 不能觉察整体,着眼于单个字母,陷入死胡同而无法求解。
巩固练习:
若代数式2a2+3a+1的值为5,求代数式4a2+6a+8的值.
五.课时小结
1、我们在探索规律时,要认真观察数据,先把数据中不变的量分离出来,再把变化中的共同规律归纳出来,列成式子,然后进行验证,从而得出正确的能反应数量关系的规律。
2、有些代数式没有给出字母的值,却已知与字母相关的一个“小代数式”的值,而原代数式的值恰好是由这样的“小代数式”构成的,这时,把“小代数式”看成一个整体,用整体代入法求值。
六.课堂作业
1.填表.
2x 2
2x+1 9 3
( http: / / www.21cnjy.com )
3.用火柴棒按下面的方式搭成图形.
(1)根据上述图形填写下表.
图形编号 ① ② ③
火柴棒根数
(2)第n个图形需要火柴棒根数为s,写出用n表示s的公式.
(3)当n=10时,求出s值.
( http: / / www.21cnjy.com )
4.当x=3,y=时,求下列代数式的值:(1)2x2-4xy2+4y; (2).
当x-y=2时,求代数式(x-y)2+2(y-x)+5的值.
6.小明读一本共m页的书,第一天读了该书的,第二天读了剩下的.
(1)用代数式表示小明两天共读了多少页.
(2)求当m=120时,小明两天读的页数.
7.当m=2,n=1时,
(1)求代数式(m+2)2和m2+2mn+n2的值.
(2)写出这两个代数式值的关系.
(3)当m=5,n=-2时,上述的结论是否仍成立?
(4)根据(1)、(2),你能用简便方法算出,当m=0.125,n=0.875时,m2+2mn+n2的值吗?
教学目标: 1、了解代数式的值的意义,会计算代数式的值。
2、在计算代数式的值的过程中感受数量的变化及其联系,感悟整体代入的思想。3、在探索规律的过程中感悟从具体到抽象的归纳思想方法。
教学重点:求代数式的值
教学难点:一般到特殊,具体到抽象的归纳思想
教学准备:配套课件,三角板
教学过程:
创设情境,设凝激思--------引题
工地上有一堆圆形钢管,第一层有2根,第二层3根,第三层4根,……
你能说出从第一层到第八层共有多少根吗?到第n层共有多少根呢?
二.实际问题引入,
(分组讨论)
摆放餐桌和椅子问题:
餐桌横放:
(1)1张餐桌可坐6人,2张餐桌可 人。
(2)按照上图的方式继续排列餐桌,完成下表:
桌子张数 3 4 5 6 ……
可坐人数
(3)探索餐桌张数n与可坐人数w之间的关系。
15张餐桌这样排,可坐多少人?
餐桌竖放:
( http: / / www.21cnjy.com )
若按下图方式将桌子拼在一起。
(1)2张桌子拼在一起可坐 人,3张桌子可坐 人,n张桌子可坐 人。
(2)一家餐厅有40张这样的长方形桌子,按照上图方式每5张拼成1张大桌子,则40张桌子可拼成8张大桌子,共可坐 人
(3)在(2)中,若改成每8张桌子拼成1张大桌子,则共可坐 人。
三.拓展练习:
某种药品的数量与总价关系如下表:
数量(克) 总价(元)
1 2.1
2 4.1
3 6.1
4 8.1
…… ……
写出药品数量x(克)与总价y(元)之间的关系。
四.引申思考,发散思维
已知a+b=3,求代数式(a+b)2+a+6+b的值.
思路点拨: 本例中字母 a,b的值并不知 ( http: / / www.21cnjy.com )道,如果根据已知a+b=3来求出a,b是不可能的。观察代数式发现,其中a+b是以整体出现的,所以可将a+b直接代入原代数式求值。
解: 当 a+b=3时,
(a+b)2+a+6+b=(a+b)2 +(a +b)+6
=32+3+6
=18
误点剖析: 不能觉察整体,着眼于单个字母,陷入死胡同而无法求解。
巩固练习:
若代数式2a2+3a+1的值为5,求代数式4a2+6a+8的值.
五.课时小结
1、我们在探索规律时,要认真观察数据,先把数据中不变的量分离出来,再把变化中的共同规律归纳出来,列成式子,然后进行验证,从而得出正确的能反应数量关系的规律。
2、有些代数式没有给出字母的值,却已知与字母相关的一个“小代数式”的值,而原代数式的值恰好是由这样的“小代数式”构成的,这时,把“小代数式”看成一个整体,用整体代入法求值。
六.课堂作业
1.填表.
2x 2
2x+1 9 3
( http: / / www.21cnjy.com )
3.用火柴棒按下面的方式搭成图形.
(1)根据上述图形填写下表.
图形编号 ① ② ③
火柴棒根数
(2)第n个图形需要火柴棒根数为s,写出用n表示s的公式.
(3)当n=10时,求出s值.
( http: / / www.21cnjy.com )
4.当x=3,y=时,求下列代数式的值:(1)2x2-4xy2+4y; (2).
当x-y=2时,求代数式(x-y)2+2(y-x)+5的值.
6.小明读一本共m页的书,第一天读了该书的,第二天读了剩下的.
(1)用代数式表示小明两天共读了多少页.
(2)求当m=120时,小明两天读的页数.
7.当m=2,n=1时,
(1)求代数式(m+2)2和m2+2mn+n2的值.
(2)写出这两个代数式值的关系.
(3)当m=5,n=-2时,上述的结论是否仍成立?
(4)根据(1)、(2),你能用简便方法算出,当m=0.125,n=0.875时,m2+2mn+n2的值吗?
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
