2.4 一元一次不等式 课件(共45张PPT)2023-—2024学年北师大版数学八年级下册
文档属性
| 名称 | 2.4 一元一次不等式 课件(共45张PPT)2023-—2024学年北师大版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 22:29:01 | ||
图片预览










文档简介
(共45张PPT)
2.4 一元一次不等式
第1课时
配套北师大版
1.经历一元一次不等式概念的形成过程.
2.会解简单的一元一次不等式,并能在数轴上表示其解集.
3.通过设置情境,经历一元一次不等式的形成过程,类比理解一元一次不等式的解法步骤.
4.初步认识一元一次不等式的应用价值,发展学生分析、解决问题的能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
一元一次不等式
复习回顾
思考:什么叫一元一次方程
只含有一个未知数,并且未知数的指数都是1,像这样的方程叫做一元一次方程.
解一元一次方程的步骤:
(1)去分母; (2)去括号;(3)移项; (4)合并同类项; (5)系数化为1.
复习回顾
不等式性质1:不等式两边加(或减)同一个整式,不等号的方向不变.
不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变.
不等式的基本性质:
探究
问题:观察下列不等式:
6+3x>30,x+17≤5x,x>5 , .
共同的特征:
这些不等式有哪些共同特点?
①只含有一个未知数;
②未知数的次数都是1;
③不等号的左右两边都是整式.
探究
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
一元一次不等式概念:
一元一次方程与一元一次不等式的区别:
连接两边整式的符号:前者是等号,而后者是不等号.
练一练:下列式子中,哪些是一元一次不等式
(1) 5x+2>1;
(2)2x+3≤5x+3;
(3) 7x+4=5;
(4) x+4y>6;
(5) 3x(x–1)<5x;
(6)
左边不是整式.
含有两个未知数.
是一元一次方程.
化简后是3x2-3x<5x
判断一个不等式是否为一元一次不等式,必须化简整理后再判断.
做一做
在前面几节课中,你列出了哪些一元一次不等式?试举几例.
2x+3 <4
3x ≤x-3
想一想
如何解一元一次不等式呢?
探究
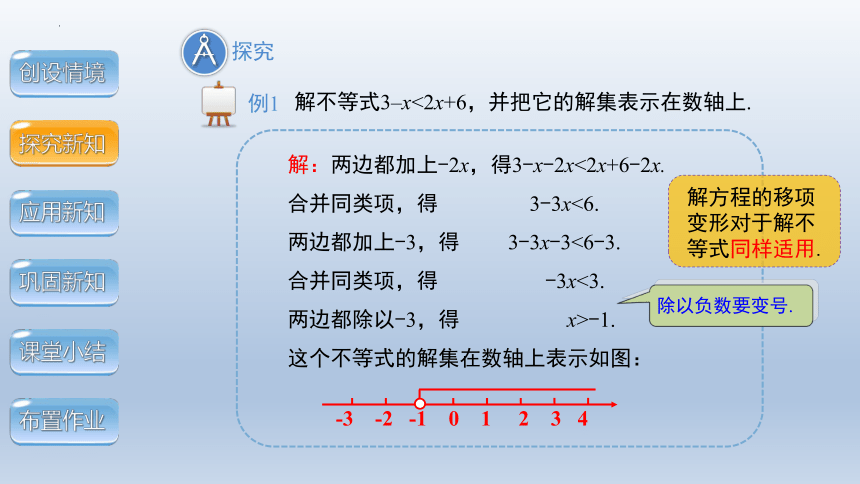
解:两边都加上-2x,得3-x-2x<2x+6-2x.
合并同类项,得 3-3x<6.
两边都加上-3,得 3-3x-3<6-3.
合并同类项,得 -3x<3.
两边都除以-3,得 x>-1.
这个不等式的解集在数轴上表示如图:
解不等式3–x<2x+6,并把它的解集表示在数轴上.
-3 -2 -1 0 1 2 3 4
例1
除以负数要变号.
解方程的移项变形对于解不等式同样适用.
探究
例2
解不等式,并把它的解集表示在数轴上.
解:去分母,得 3(x-2)≥2(7-x)
去括号,得 3x-6≥14-2x
移项、合并同类项,得 5x≥20
两边都除以5,得 x≥4
0 1 2 3 4 5 6 7
方程两边同乘6,将分母去掉.
将同类项放在一起.
这个不等式的解集在数轴上表示如图:
注:解集x≥4中包含4,所以在数轴上将表示4的点画成实心圆点.
根据不等式性质2,不等式两边同除5.
探究
归纳:解一元一次不等式的步骤:
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项; (5)系数化为1.
这些步骤中,要特别注意:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
典型例题
例
解:由方程的解的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得 -2x>-6,
两边都除以-2,得 x<3.
在数轴上表示如图:
已知方程ax+12=0的解是x=3,求关于x的不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
-1
0
1
2
3
4
5
6
其中正整数解有1和2.
先根据方程的解的定义,求出的值,再利用不等式的基本性质解不等式.最后从不等式的解集中找出适合条件的正整数解.
随堂练习
1.若5x2m-1-8>5是关于x的一元一次不等式,则m的值为( )
A.0 B.1 C.2 D.3
B
2.不等式 的解集为x>2,则m的值为( )
A. 4 B.2
C. D.
B
4.不等式 的负整数解有( )
A.1个 B.2个
C.3个 D.4个
随堂练习
3.将不等式3x-2<1的解集表示在数轴上,正确的是( )
A. B.
C. D.
D
A
随堂练习
解:(1) 5x<200,
把x的系数化为1得,x<40,
在数轴上表示为:
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
-10
0
10
20
30
40
50
60
随堂练习
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
解:(2)
去分母得, -(x+1)<6,
去括号得, -x-1<6,
移项得, -x<6+1,
合并同类项得, -x<7,
把x的系数化为1得,x>-7,
在数轴上表示为:
-7
-6
-5
-4
-3
-2
-1
0
随堂练习
解:(3) x-4≥2(x+2)
去括号得, x-4≥2x+4,
移项得, x-2x≥4+4,
合并同类项得, -x≥8,
把x的系数化为1得,x≤-8,
在数轴上表示为:
-10
-8
-6
-4
-2
0
2
4
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
随堂练习
解:(4) 去分母,得 3(x-1)<2(4x-5), 去括号,得 3x-3<8x-10,
移项、合并同类项,得 5x>7,
不等式两边都除以5,得x> ,
不等式的解集在数轴上表示为:
-1
0
1
2
3
4
5
6
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
随堂练习
6.求不等式 4(x+1)≤24 的正整数解.
解:去括号,得 4x +4≤24.
移项、合并同类项,得4x ≤20.
两边都除以4,得 x ≤ 5.
不等式的解集在数轴上表示为:
所以原不等式的正整数解为1,2,3,4,5.
-1
0
1
2
3
4
5
6
概念:
一元一次不等式
解一元一次不等式步骤:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项; (5)系数化为1.
教科书习题2.4
第1、2、3题
再见
2.4 一元一次不等式
第2课时
配套北师大版
1.能根据实际问题中的数量关系,列一元一次不等式求解.
2.初步感知实际问题对不等式解集的影响,积累利用一元一次不等式解决简单实际问题的经验.
3.结合具体问题,了解不等式的意义,初步体会一元一次不等式的应用价值.
4.发展学生分析问题、解决问题的能力;体会数学建模思想,提升应用数学知识解答实际问题的兴趣与能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
一元一次不等式
复习回顾
思考:什么叫一元一次不等式
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
问题:下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
复习回顾
一元一次不等式的解法:
解一元一次不等式,要根据不等式的性质,将不等式逐步化为x>a(x≥a)或x其一般步骤:(1)去分母;(2)去括号;(3)移项;
(4)合并同类项;(5)系数化为1(注意不等号方向是否改变).
复习回顾
应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
探究
问题:某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润率不能少于5%. 请你帮助售货员计算一下,这种商品最多可以按几折销售?
【分析】 本题涉及的数量关系是:
(售价-进价)÷进价≥ 5%.
解:设该商品可以打x折销售,
则 (300×0.1x-200)÷200≥5%,
解得 x ≥7.
答:这种商品最多可以按七折销售.
你是从语句中哪些地方看出不等关系的
1.这次单元考试小华数学考得不好,没有达到自己定的90分的目标.
2.五一小华跟爸爸妈妈去北京旅游,发现各景点门票都很贵,没有低于100元的.
3.在路上小华看到一个限速标志,爸爸告诉他这是限制最高时速为每小时40千米.
直接型的不等关系:可以通过一些关键词,如“大于,
小于,不大于,不小于,最多,至少,不够,超过”等.
做一做
你是从语句中哪些地方看出不等关系的
4.由于要出去旅游,小华去商场买T恤衫,他身上带着80块钱.
5.小华买了盒奶上面写着保质期为6个月.
隐含型的不等关系:不等关系比较隐蔽,表面上没有关键词,需要分析题意,再依据生活实际得出不等关系.
做一做
探究
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明的得分为优秀(85分或85分以上),小明至少答对了几道题?
此实际问题中的不等关系是什么?
不等关系是:小明的得分≥85
设小明答对了 x 道题,则他答错和不答的共有多少道题?
答错和不答的共有(25-x)道题.
探究
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明的得分为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了 x 道题,则他答错和不答的共有
(25-x)道题.
根据题意,得 4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
所以,小明至少答对了22道题.
利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
归纳
探究
例1 一辆客车从甲地开往乙地,出发 10 min 后,一辆轿车也从甲地开往乙地,轿车的速度是 120 km/h,轿车出发 30 min 内就超过了客车,则客车的速度小于多少
甲
乙
10 min后
客车
轿车
不等关系是:客车速度× <轿车速度×
探究
解:设客车的速度是x km/h,根据题意,得
解这个不等式,得 x < 90.
所以,客车的速度小于 90 km/h.
例1 一辆客车从甲地开往乙地,出发 10 min 后,一辆轿车也从甲地开往乙地,轿车的速度是 120 km/h,轿车出发 30 min 内就超过了客车,则客车的速度小于多少
某种商品的进价为 400 元,出售时标价为 500 元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于10%,则最低可打几折
典型例题
例2
【分析】 设可以打x折,由题意得不等关系:(售价-进价)÷进价≥ 10%,根据不等关系列出不等式,再解即可.
解:设可以打x折,由题意得:
≥10%
解得:x≥8.8,
所以,最低可以打8.8折.
小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元,一盒方便面3元,他买了5盒方便面,他最多还能买多少根火腿肠?
典型例题
例3
解:设他还可买x根火腿肠.
根据题意,得 2x+3×5≤26.
解这个不等式,得x≤5.5.
因为在这一问题中,x只能取正整数,所以小明最多还能买5根火腿肠.
提示:注意问题的实际意义.
【分析】 设他还能买x根火腿肠,不等关系为:x根火腿肠的价格+5盒方便面的价格≤26,依此列出不等式,求解即可.
随堂练习
1.某品牌自行车进价是每辆800元,标价是每辆1 200元,店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润不低于5%,则最多可打几折( )
A.5 B.6 C.7 D.8
2.小明准备用节省的零花钱买一台随身音响,他已存有45元,计划从现在起以后每月节省30元,直到他至少有300元.设x月后他至少有300元,则符合题意的不等式是( )
A.30x-45≥300 B.30x+45≥300
C.30x-45≤300 D.30x+45≤300
B
C
随堂练习
3.甲、乙两种运输车将46 t物资运往某区,甲种运输车载重为5 t,乙种运输车载重为4 t,共安排运输车10辆,则甲种运输车至少应安排( )
A.4辆 B.5辆 C.6辆 D.7辆
C
4.小明用30元钱买笔记本和练习本共30本,已知每个笔记本4元,每个练习本4角,那么他最多能买笔记本( )
A.7本 B.6本 C.5本 D.4本
C
随堂练习
5.有10名菜农,每人可种茄子3亩或辣椒2亩,已知茄子每亩可收入0.5万元,辣椒每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能安排 人种茄子.
6. 一个工程队原定在10天内至少要挖土600m ,在前两天一共完成了120m ,由于整个工程调整工期,要求提前两天完成挖土任务.问以后几天内,平均每天至少要挖土 m .
4
80
随堂练习
解:设需要购买x块地板砖,根据题意,得
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
小明至少要购买56块地板砖.
7.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
随堂练习
8. 某学校学生会组织七年级和八年级共60名同学参加环保活动,七年级学生平均每人收集15个废弃塑料瓶,八年级学生平均每人收集20个废弃塑料瓶.为了保证所收集的塑料瓶总数不少于1000个,至少需要多少名八年级学生参加活动?
解:设参加的八年级学生为x人,则参加活动的七年级学生为(60-x)名,
根据题意得 15×(60-x)+20x≥1000
解不等式,得 x≥20
所以至少需要20名八年级学生参加活动.
一元一次不等式
利用不等式解决实际问题的步骤:
实际问题
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
解题关键:
根据题意,找出不等关系.
直接不等关系
隐含不等关系
教科书 习题2.5
第2、3、4题
再见
2.4 一元一次不等式
第1课时
配套北师大版
1.经历一元一次不等式概念的形成过程.
2.会解简单的一元一次不等式,并能在数轴上表示其解集.
3.通过设置情境,经历一元一次不等式的形成过程,类比理解一元一次不等式的解法步骤.
4.初步认识一元一次不等式的应用价值,发展学生分析、解决问题的能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
一元一次不等式
复习回顾
思考:什么叫一元一次方程
只含有一个未知数,并且未知数的指数都是1,像这样的方程叫做一元一次方程.
解一元一次方程的步骤:
(1)去分母; (2)去括号;(3)移项; (4)合并同类项; (5)系数化为1.
复习回顾
不等式性质1:不等式两边加(或减)同一个整式,不等号的方向不变.
不等式性质2:不等式两边都乘(或除以)同一个正数,不等号的方向不变.
不等式性质3:不等式两边都乘(或除以)同一个负数,不等号的方向改变.
不等式的基本性质:
探究
问题:观察下列不等式:
6+3x>30,x+17≤5x,x>5 , .
共同的特征:
这些不等式有哪些共同特点?
①只含有一个未知数;
②未知数的次数都是1;
③不等号的左右两边都是整式.
探究
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
一元一次不等式概念:
一元一次方程与一元一次不等式的区别:
连接两边整式的符号:前者是等号,而后者是不等号.
练一练:下列式子中,哪些是一元一次不等式
(1) 5x+2>1;
(2)2x+3≤5x+3;
(3) 7x+4=5;
(4) x+4y>6;
(5) 3x(x–1)<5x;
(6)
左边不是整式.
含有两个未知数.
是一元一次方程.
化简后是3x2-3x<5x
判断一个不等式是否为一元一次不等式,必须化简整理后再判断.
做一做
在前面几节课中,你列出了哪些一元一次不等式?试举几例.
2x+3 <4
3x ≤x-3
想一想
如何解一元一次不等式呢?
探究
解:两边都加上-2x,得3-x-2x<2x+6-2x.
合并同类项,得 3-3x<6.
两边都加上-3,得 3-3x-3<6-3.
合并同类项,得 -3x<3.
两边都除以-3,得 x>-1.
这个不等式的解集在数轴上表示如图:
解不等式3–x<2x+6,并把它的解集表示在数轴上.
-3 -2 -1 0 1 2 3 4
例1
除以负数要变号.
解方程的移项变形对于解不等式同样适用.
探究
例2
解不等式,并把它的解集表示在数轴上.
解:去分母,得 3(x-2)≥2(7-x)
去括号,得 3x-6≥14-2x
移项、合并同类项,得 5x≥20
两边都除以5,得 x≥4
0 1 2 3 4 5 6 7
方程两边同乘6,将分母去掉.
将同类项放在一起.
这个不等式的解集在数轴上表示如图:
注:解集x≥4中包含4,所以在数轴上将表示4的点画成实心圆点.
根据不等式性质2,不等式两边同除5.
探究
归纳:解一元一次不等式的步骤:
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项; (5)系数化为1.
这些步骤中,要特别注意:不等式两边都乘(或除以)同一个负数,必须改变不等号的方向.这是与解一元一次方程不同的地方.
典型例题
例
解:由方程的解的定义,把x=3代入ax+12=0中,
得 a=-4.
把a=-4代入(a+2)x>-6中,
得 -2x>-6,
两边都除以-2,得 x<3.
在数轴上表示如图:
已知方程ax+12=0的解是x=3,求关于x的不等式(a+2)x>-6的解集,并在数轴上表示出来,其中正整数解有哪些?
-1
0
1
2
3
4
5
6
其中正整数解有1和2.
先根据方程的解的定义,求出的值,再利用不等式的基本性质解不等式.最后从不等式的解集中找出适合条件的正整数解.
随堂练习
1.若5x2m-1-8>5是关于x的一元一次不等式,则m的值为( )
A.0 B.1 C.2 D.3
B
2.不等式 的解集为x>2,则m的值为( )
A. 4 B.2
C. D.
B
4.不等式 的负整数解有( )
A.1个 B.2个
C.3个 D.4个
随堂练习
3.将不等式3x-2<1的解集表示在数轴上,正确的是( )
A. B.
C. D.
D
A
随堂练习
解:(1) 5x<200,
把x的系数化为1得,x<40,
在数轴上表示为:
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
-10
0
10
20
30
40
50
60
随堂练习
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
解:(2)
去分母得, -(x+1)<6,
去括号得, -x-1<6,
移项得, -x<6+1,
合并同类项得, -x<7,
把x的系数化为1得,x>-7,
在数轴上表示为:
-7
-6
-5
-4
-3
-2
-1
0
随堂练习
解:(3) x-4≥2(x+2)
去括号得, x-4≥2x+4,
移项得, x-2x≥4+4,
合并同类项得, -x≥8,
把x的系数化为1得,x≤-8,
在数轴上表示为:
-10
-8
-6
-4
-2
0
2
4
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
随堂练习
解:(4) 去分母,得 3(x-1)<2(4x-5), 去括号,得 3x-3<8x-10,
移项、合并同类项,得 5x>7,
不等式两边都除以5,得x> ,
不等式的解集在数轴上表示为:
-1
0
1
2
3
4
5
6
5.解下列不等式,并把它们的解集分别表示在数轴上.
(1)5x<200; (2) (3)x-4≥2(x+2); (4)
随堂练习
6.求不等式 4(x+1)≤24 的正整数解.
解:去括号,得 4x +4≤24.
移项、合并同类项,得4x ≤20.
两边都除以4,得 x ≤ 5.
不等式的解集在数轴上表示为:
所以原不等式的正整数解为1,2,3,4,5.
-1
0
1
2
3
4
5
6
概念:
一元一次不等式
解一元一次不等式步骤:
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
(1)去分母; (2)去括号; (3)移项;
(4)合并同类项; (5)系数化为1.
教科书习题2.4
第1、2、3题
再见
2.4 一元一次不等式
第2课时
配套北师大版
1.能根据实际问题中的数量关系,列一元一次不等式求解.
2.初步感知实际问题对不等式解集的影响,积累利用一元一次不等式解决简单实际问题的经验.
3.结合具体问题,了解不等式的意义,初步体会一元一次不等式的应用价值.
4.发展学生分析问题、解决问题的能力;体会数学建模思想,提升应用数学知识解答实际问题的兴趣与能力.
学习目标
重点
难点
准备好了吗?一起去探索吧!
一元一次不等式
复习回顾
思考:什么叫一元一次不等式
不等式的左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式.
问题:下列式子中,一元一次不等式有( )
①3x-1≥4
② 2+3x>6
③ 3- <5
④
⑤
⑥ x+xy≥y2
⑦x>0
A.5个
B.4个
C.6个
D.3个
A
√
√
×
√
√
×
√
复习回顾
一元一次不等式的解法:
解一元一次不等式,要根据不等式的性质,将不等式逐步化为x>a(x≥a)或x
(4)合并同类项;(5)系数化为1(注意不等号方向是否改变).
复习回顾
应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
探究
问题:某种商品进价为200元,标价300元出售,商场规定可以打折销售,但其利润率不能少于5%. 请你帮助售货员计算一下,这种商品最多可以按几折销售?
【分析】 本题涉及的数量关系是:
(售价-进价)÷进价≥ 5%.
解:设该商品可以打x折销售,
则 (300×0.1x-200)÷200≥5%,
解得 x ≥7.
答:这种商品最多可以按七折销售.
你是从语句中哪些地方看出不等关系的
1.这次单元考试小华数学考得不好,没有达到自己定的90分的目标.
2.五一小华跟爸爸妈妈去北京旅游,发现各景点门票都很贵,没有低于100元的.
3.在路上小华看到一个限速标志,爸爸告诉他这是限制最高时速为每小时40千米.
直接型的不等关系:可以通过一些关键词,如“大于,
小于,不大于,不小于,最多,至少,不够,超过”等.
做一做
你是从语句中哪些地方看出不等关系的
4.由于要出去旅游,小华去商场买T恤衫,他身上带着80块钱.
5.小华买了盒奶上面写着保质期为6个月.
隐含型的不等关系:不等关系比较隐蔽,表面上没有关键词,需要分析题意,再依据生活实际得出不等关系.
做一做
探究
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明的得分为优秀(85分或85分以上),小明至少答对了几道题?
此实际问题中的不等关系是什么?
不等关系是:小明的得分≥85
设小明答对了 x 道题,则他答错和不答的共有多少道题?
答错和不答的共有(25-x)道题.
探究
一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道题扣1分.在这次竞赛中,小明的得分为优秀(85分或85分以上),小明至少答对了几道题?
解:设小明答对了 x 道题,则他答错和不答的共有
(25-x)道题.
根据题意,得 4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
所以,小明至少答对了22道题.
利用不等式来解决实际问题的步骤是什么?
实际问题
设未知数,列不等式
数学问题
(一元一次不等式)
解
不
等
式
数学问题的解
(一元一次不等式的解集)
实际问题的解答
检验
数学建模
归纳
探究
例1 一辆客车从甲地开往乙地,出发 10 min 后,一辆轿车也从甲地开往乙地,轿车的速度是 120 km/h,轿车出发 30 min 内就超过了客车,则客车的速度小于多少
甲
乙
10 min后
客车
轿车
不等关系是:客车速度× <轿车速度×
探究
解:设客车的速度是x km/h,根据题意,得
解这个不等式,得 x < 90.
所以,客车的速度小于 90 km/h.
例1 一辆客车从甲地开往乙地,出发 10 min 后,一辆轿车也从甲地开往乙地,轿车的速度是 120 km/h,轿车出发 30 min 内就超过了客车,则客车的速度小于多少
某种商品的进价为 400 元,出售时标价为 500 元,后来由于该商品积压,商店准备打折出售,但要保持利润率不低于10%,则最低可打几折
典型例题
例2
【分析】 设可以打x折,由题意得不等关系:(售价-进价)÷进价≥ 10%,根据不等关系列出不等式,再解即可.
解:设可以打x折,由题意得:
≥10%
解得:x≥8.8,
所以,最低可以打8.8折.
小明准备用26元钱买火腿肠和方便面,已知一根火腿肠2元,一盒方便面3元,他买了5盒方便面,他最多还能买多少根火腿肠?
典型例题
例3
解:设他还可买x根火腿肠.
根据题意,得 2x+3×5≤26.
解这个不等式,得x≤5.5.
因为在这一问题中,x只能取正整数,所以小明最多还能买5根火腿肠.
提示:注意问题的实际意义.
【分析】 设他还能买x根火腿肠,不等关系为:x根火腿肠的价格+5盒方便面的价格≤26,依此列出不等式,求解即可.
随堂练习
1.某品牌自行车进价是每辆800元,标价是每辆1 200元,店庆期间,商场为了答谢顾客,进行打折促销活动,但是要保证利润不低于5%,则最多可打几折( )
A.5 B.6 C.7 D.8
2.小明准备用节省的零花钱买一台随身音响,他已存有45元,计划从现在起以后每月节省30元,直到他至少有300元.设x月后他至少有300元,则符合题意的不等式是( )
A.30x-45≥300 B.30x+45≥300
C.30x-45≤300 D.30x+45≤300
B
C
随堂练习
3.甲、乙两种运输车将46 t物资运往某区,甲种运输车载重为5 t,乙种运输车载重为4 t,共安排运输车10辆,则甲种运输车至少应安排( )
A.4辆 B.5辆 C.6辆 D.7辆
C
4.小明用30元钱买笔记本和练习本共30本,已知每个笔记本4元,每个练习本4角,那么他最多能买笔记本( )
A.7本 B.6本 C.5本 D.4本
C
随堂练习
5.有10名菜农,每人可种茄子3亩或辣椒2亩,已知茄子每亩可收入0.5万元,辣椒每亩可收入0.8万元,要使总收入不低于15.6万元,则最多只能安排 人种茄子.
6. 一个工程队原定在10天内至少要挖土600m ,在前两天一共完成了120m ,由于整个工程调整工期,要求提前两天完成挖土任务.问以后几天内,平均每天至少要挖土 m .
4
80
随堂练习
解:设需要购买x块地板砖,根据题意,得
5×4≤0.6×0.6x
解得 x ≥ 55.6
由于地板砖的数目必须是整数,所以x的最小值为56.
小明至少要购买56块地板砖.
7.小明家的客厅长5 m,宽4 m.现在想购买边长为60 cm的正方形地板砖把地面铺满,至少需要购买多少块这样的地板砖?
随堂练习
8. 某学校学生会组织七年级和八年级共60名同学参加环保活动,七年级学生平均每人收集15个废弃塑料瓶,八年级学生平均每人收集20个废弃塑料瓶.为了保证所收集的塑料瓶总数不少于1000个,至少需要多少名八年级学生参加活动?
解:设参加的八年级学生为x人,则参加活动的七年级学生为(60-x)名,
根据题意得 15×(60-x)+20x≥1000
解不等式,得 x≥20
所以至少需要20名八年级学生参加活动.
一元一次不等式
利用不等式解决实际问题的步骤:
实际问题
根据题意列不等式
↓
解一元一次不等式
→
→
根据实际问题找出符合条件的解集或整数解
↑
得出解决问题的答案
解题关键:
根据题意,找出不等关系.
直接不等关系
隐含不等关系
教科书 习题2.5
第2、3、4题
再见
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
