河南省南阳市唐河县2021-2022学年八年级上学期期末数学试题 (含答案)
文档属性
| 名称 | 河南省南阳市唐河县2021-2022学年八年级上学期期末数学试题 (含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 06:35:29 | ||
图片预览

文档简介
2022年秋期期终阶段性文化素质监测八年级
数 学 试 题
注意事项:
1.本试卷共6页,满分120分,考试时间100分钟。
2.试题卷上不要答题,请用0.5毫米黑色签字水笔直接把答案写在答题卡上。答在试题卷上的答案无效。
3.答题前,考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置上。
一、选择题(每小题3分,共30分)
1.数据:,,,,其中是无理数的是
A. B. C. D.
2.下列运算正确的是
A. B.
C. D.
3.已知△ABC中,,求证:,下面写出运用反证法证明这个命题的四个步骤:
①∴,这与三角形内角和为矛盾
②因此假设不成立.∴
③假设在△ABC中,
④由,得,即.
这四个步骤正确的顺序应是
A.④③①② B.③④②① C.①②③④ D.③④①②
4.有下列条件不能判断△ABC是直角三角形的是
A. B.
C. D.
5.如图,四边形ABCD是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是
A. B. C. D.
第5题图 第7题图
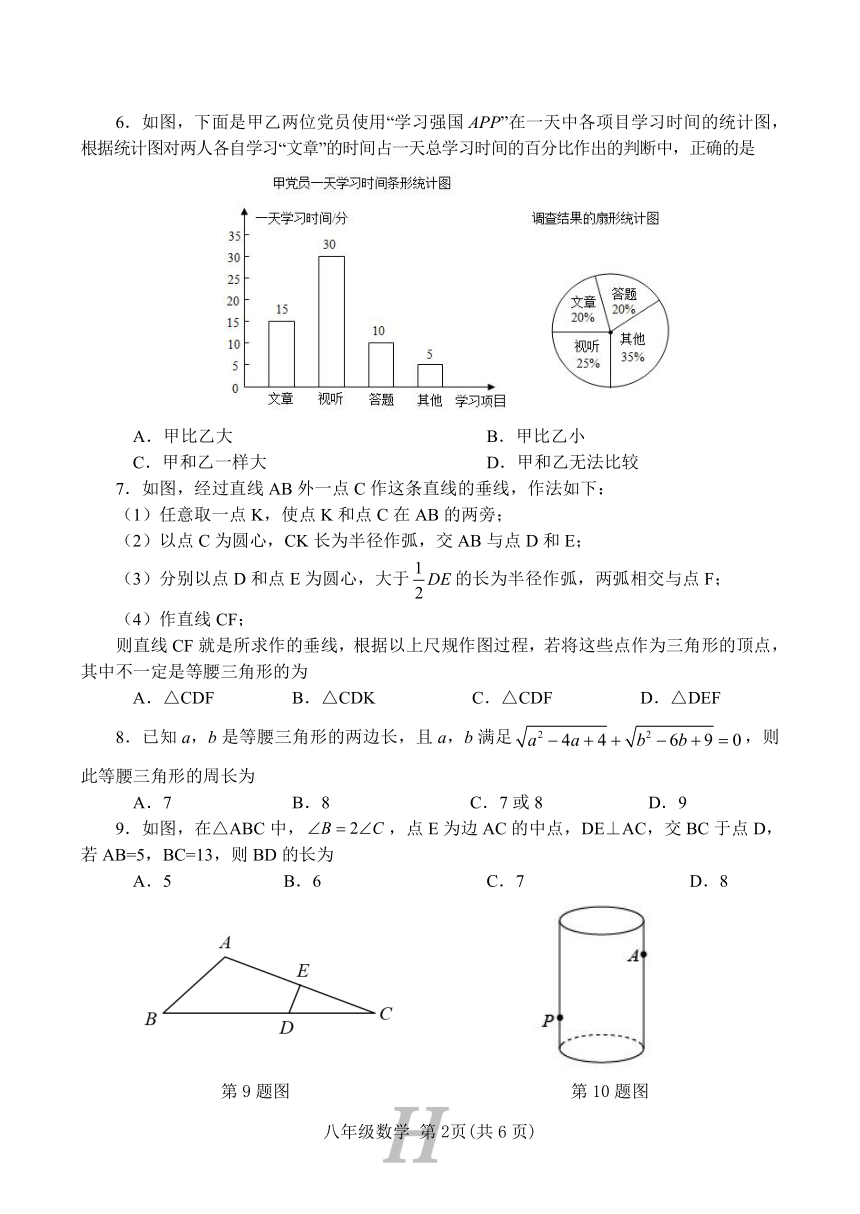
6.如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是
A.甲比乙大 B.甲比乙小
C.甲和乙一样大 D.甲和乙无法比较
7.如图,经过直线AB外一点C作这条直线的垂线,作法如下:
任意取一点K,使点K和点C在AB的两旁;
以点C为圆心,CK长为半径作弧,交AB与点D和E;
分别以点D和点E为圆心,大于的长为半径作弧,两弧相交与点F;
作直线CF;
则直线CF就是所求作的垂线,根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为
A.△CDF B.△CDK C.△CDF D.△DEF
8.已知a,b是等腰三角形的两边长,且a,b满足,则此等腰三角形的周长为
A.7 B.8 C.7或8 D.9
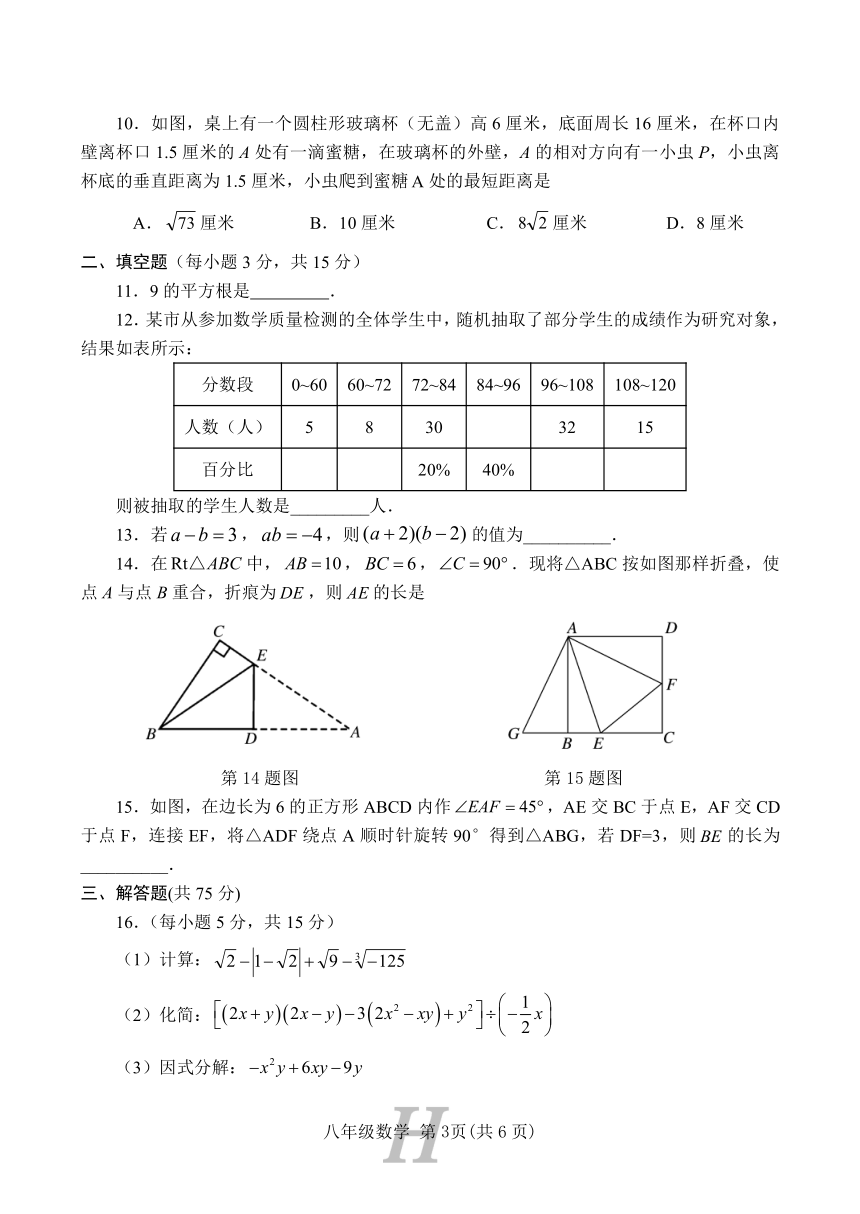
9.如图,在△ABC中,,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为
A.5 B.6 C.7 D.8
第9题图 第10题图
10.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是
A.厘米 B.10厘米 C.厘米 D.8厘米
二、填空题(每小题3分,共15分)
11.9的平方根是 .
12.某市从参加数学质量检测的全体学生中,随机抽取了部分学生的成绩作为研究对象,结果如表所示:
分数段 0~60 60~72 72~84 84~96 96~108 108~120
人数(人) 5 8 30 32 15
百分比 20% 40%
则被抽取的学生人数是_________人.
13.若,,则值为__________.
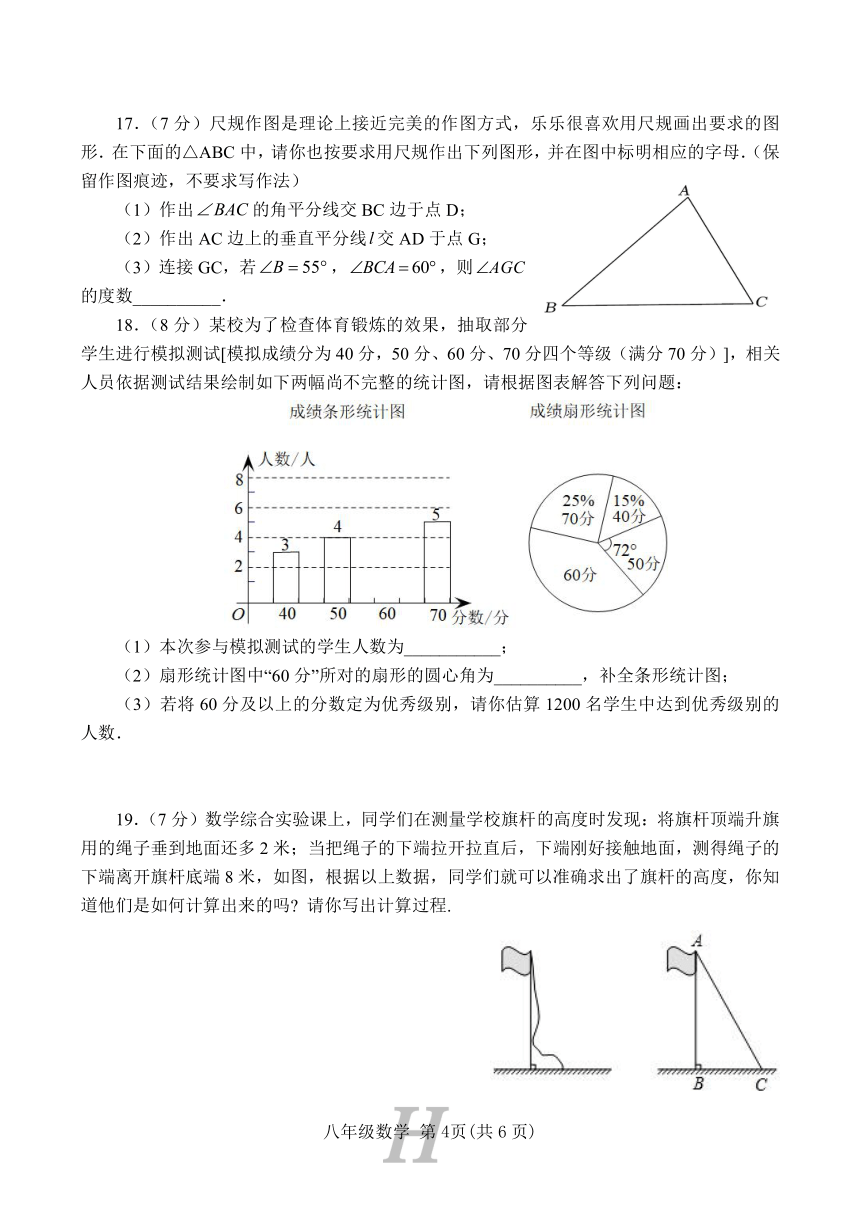
14.在中,,,.现将△ABC按如图那样折叠,使点A与点B重合,折痕为,则的长是
第14题图 第15题图
15.如图,在边长为6的正方形ABCD内作,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG,若DF=3,则的长为__________.
三、解答题(共75分)
16.(每小题5分,共15分)
(1)计算:
(2)化简:
(3)因式分解:
17.(7分)尺规作图是理论上接近完美的作图方式,乐乐很喜欢用尺规画出要求的图形.在下面的△ABC中,请你也按要求用尺规作出下列图形,并在图中标明相应的字母.(保留作图痕迹,不要求写作法)
(1)作出的角平分线交BC边于点D;
(2)作出AC边上的垂直平分线交AD于点G;
(3)连接GC,若,,则的度数__________.
18.(8分)某校为了检查体育锻炼的效果,抽取部分学生进行模拟测试[模拟成绩分为40分,50分、60分、70分四个等级(满分70分)],相关人员依据测试结果绘制如下两幅尚不完整的统计图,请根据图表解答下列问题:
(1)本次参与模拟测试的学生人数为___________;
(2)扇形统计图中“60分”所对的扇形的圆心角为__________,补全条形统计图;
(3)若将60分及以上的分数定为优秀级别,请你估算1200名学生中达到优秀级别的人数.
19.(7分)数学综合实验课上,同学们在测量学校旗杆高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开拉直后,下端刚好接触地面,测得绳子的下端离开旗杆底端8米,如图,根据以上数据,同学们就可以准确求出了旗杆的高度,你知道他们是如何计算出来的吗 请你写出计算过程.
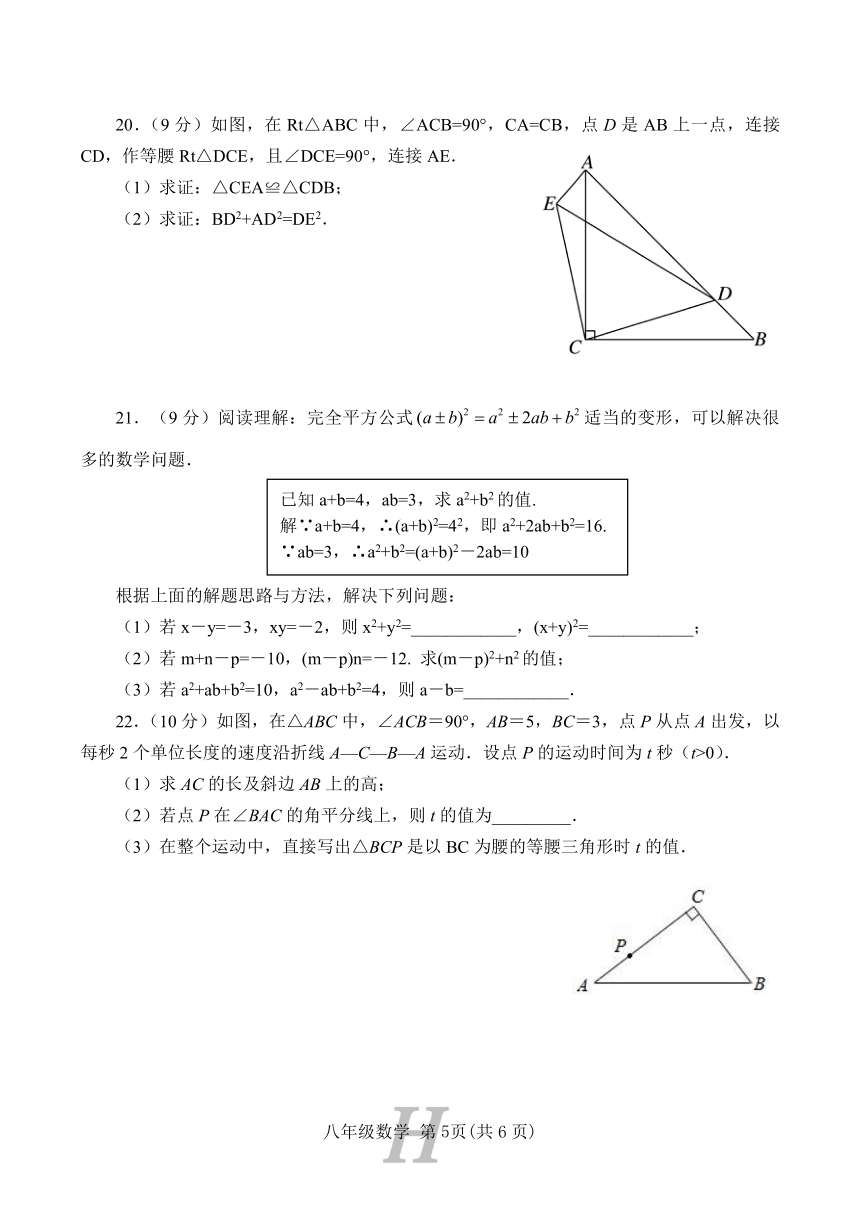
20.(9分)如图,在Rt△ABC中,∠ACB=90°,CA=CB,点D是AB上一点,连接CD,作等腰Rt△DCE,且∠DCE=90°,连接AE.
(1)求证:△CEA≌△CDB;
(2)求证:BD2+AD2=DE2.
21.(9分)阅读理解:完全平方公式适当的变形,可以解决很多的数学问题.
根据上面的解题思路与方法,解决下列问题:
(1)若x-y=-3,xy=-2,则x2+y2=____________,(x+y)2=____________;
(2)若m+n-p=-10,(m-p)n=-12. 求(m-p)2+n2的值;
(3)若a2+ab+b2=10,a2-ab+b2=4,则a-b=____________.
22.(10分)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,以每秒2个单位长度的速度沿折线A—C—B—A运动.设点P的运动时间为t秒(t>0).
(1)求AC的长及斜边AB上的高;
(2)若点P在∠BAC的角平分线上,则t的值为_________.
(3)在整个运动中,直接写出△BCP是以BC为腰的等腰三角形时t的值.
23.(10分)(1)【阅读验证】公元前6世纪,古希腊数学家毕达哥拉斯发现了直角三角形的三边之间的数量关系:在直角三角形中,两条直角边的平方和等于__________,这个结论在中国称之为“勾股定理”.
我国三国时期的数学家赵爽利用四个全等的直角三角形拼成如图1的“弦图”(史称“赵爽弦图”),其中四边形ABDE和四边形CFGH都是正方形,巧妙地用面积法给出了勾股定理的证明过程:
已知:Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c.
求证:a2+b2=c2
证明:由图可知S正方形ABDE=4S△ABC+S正方形FCHG
∵S正方形ABDE=c2,S△ABC=ab,正方形FCHG边长为(a-b),
∴
即.
(2)【操作发现】如图2,将等腰直角三角板ABD顶点A放在直线l上,过点B作BC⊥l,过点D作DE⊥l,垂足分别为C、E.
①求证:CE=BC+DE;
②聪聪认真观察图2后发现:如果设AC=b,BC=a,AB=c,此图也可以利用面积法证明勾股定理.请你帮聪聪完成证明过程.
(3)【拓展应用】
如图3,将图1中的这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,OC=3,直接写出该飞镖状图案的面积.
2022年秋期期终阶段性文化素质监测八年级
数学试题参考答案及评分细则
一、选择题(每小题3分,共30分)
1.C 2.D 3.D 4.A 5.B 6.A 7.C 8.C 9.D 10.B
10.把圆柱沿着点A所在母线展开,如图所示,作点A的对称点B,连接PB,则PB为所求,根据题意,得PC=8,BC=6,根据勾股定理,得PB=10,
二、填空题(每小题3分,共15分)
11.±3 12.150 13.-14 14. 15.2
三、解答题(本大题满分75分)
16.(15分)
解:(1)原式=……………………………2分
……………………………………… .5分
解:(2)
………………………………………………2分
…………………………………………………………………4分
=4x-6y.……………………………………………………………………………………5分
解:(3)
…………………………………………………………………………2分
……………………………………………………………………………5分
17.(7分)(1)解:作的角平分线交BC边于点D,如图所示,
如图所示,是的角平分线,交于点.……………………………2分
(2)作边上的垂直平分线交于点,如图所示,
如图所示,是边上的垂直平分线.………………………………………………4分
(3).………………………………………………………………………………7分
18.(8分)(1)20;……………………………………………………………2分
(2)144°,……………………………………………………………………………4分
图见详解; 条形图如下:
………………………………………5分
(3)解:根据题意,60分所占的百分比为;,……………6分
1200名学生中达到优秀级别的人数为:
(人);……………………………………………………8分
19. (7分)解:设旗杆高米,则绳子长为米,…………………………1分
∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,
在Rt△ABC中,,
∴,……………………………………………………………4分
解方程得:,…………………………………………………7分
答:旗杆高度为15米.
20.(9分)
(1)∵△ABC和△DCE都是等腰直角三角形,
∴AC=BC,CD=EC,∠ACB=∠DCE=90°,………………………………………2分
∴∠ACB-∠ACD=∠DCE-∠ACD,
∴∠ACE=∠BCD,
在△CDB与△CEA中,
……………………………………………………………4分
∴△CDB≌△CEA.…………………………………………………………5分
(2)∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,………………………………………………………………6分
由(1)得△CDB≌△CEA,
∴∠EAC=∠B=45°,BD=AE,
∴∠EAD=∠EAC+∠BAC=45°+45°=90°,………………………………………8分
∴AE2+AD2=DE2,
∴BD2+AD2=DE2.………………………………………………………………9分
21.(9分)(1)5,1 ………………………………………………(每空2分)4分
(2)解:∵m+n-p=-10,(m-p)=-12,
即(m-p)+n=-10,(m-p)n=-12,
∴(m-p)2+n2=[(m-p)+n]2-2(m-p)n………………5分
=(-10)2-2×(-12)=124;……………………………………………………7分
(3)±1 …………………………………………………………………………9分
22.(10分)(1)在△ABC中,∠ACB=90°,AB=5,BC=3,
由勾股定理得:AC==4.……………………………2分
设斜边AB上的高为h,
∵AB hAC BC,…………………………………………………3分
∴5h=3×4,
∴h=2.4.………………………………………………………………………4分
∴AC的长为4,斜边AB上的高为2.4;
…………………………………………………………………7分
(3)t的值为0.5或5或5.3…………………………(每写对一个1分)10分
(2)已知点P从点A出发,以每秒2个单位长度的速度沿折线A﹣C﹣B﹣A运动,
当点P'在∠BAC的角平分线上时,过点P'作P'D⊥AB,如图:
∵AP'平分∠BAC,P'C⊥AC,P'D⊥AB,
∴P'D=P'C=2t﹣4,
∵BC=3,
∴BP'=3﹣(2t﹣4)=7﹣2t,
在Rt△ACP'和Rt△ADP'中,
∴Rt△ACP'≌Rt△ADP'(HL),
∴AD=AC=4,
又∵AB=5,
∴BD=1,
在Rt△BDP'中,由勾股定理得:
12+(2t﹣4)2=(7﹣2t)2,
解得:t.
故答案为:.
(3)由图可知,当△BCP是等腰三角形时,点P必在线段AC或线段AB上,
①当点P在线段AC上时,此时△BCP是等腰直角三角形,
∴此时CP=BC=3,
∴AP=AC﹣CP=4﹣3=1,
∴2t=1,
∴t=0.5;
②当点P在线段AB上时,若BC=BP,
则点P运动的长度为:
AC+BC+BP=4+3+3=10,
∴2t=10,
∴t=5;
若PC=BC,如图2,过点C作CH⊥AB于点H,则BP=2BH,
在△ABC中,∠ACB=90°,AB=5,BC=3,AC=4,
∴AB CH=AC BC,
∴5CH=4×3,
∴CH,
在Rt△BCH中,由勾股定理得:
BH1.8,
∴BP=3.6,
∴点P运动的长度为:AC+BC+BP=4+3+3.6=10.6,
∴2t=10.6,
∴t=5.3;
综上,t的值为0.5或5或5.3.
23.(10分)(1)斜边的平方;……………………………………………………1分
(2)①证明:在等腰直角三角板ABD中
由已知得AD=AB,∠BAD=90°
∴∠BAC+∠DAE=90°
又∵BC⊥l,DE⊥l
∴∠BCA=∠DEA=90°,∠BAC+∠ABC=90°
∴∠DAE=∠ABC………………………………………………………………2分
∴Rt△ABC≌Rt△DAEAAS)…………………………………………………3分
∴BC=AE,AC=DE…………………………………………………4分
又∵CE=AC+AE
∴CE=BC+DE.……………………………………………………………5分
②解:由上可知BC=AE=a,AC=DE=b
∴S梯形BCED=(BC+DE)×CE=(a+b)2=a2+ab+b2……………………6分
又∵S梯形BCED=S△ABC+S△ABD+S△ADE=ab+c2+ab
∴a2+ab+b2=ab+c2+ab………………………………………………7分
整理得a2+b2=c2 ………………………………………………………8分
(3)飞镖状图案的面积为24.……………………………………………10分
解:∵飞镖模型的周长为24,观察可知4(AB+AC)=24
∴AB+AC=6
∵OB=OC
∴AB=5,OB=3,OA=4
∴飞镖状图案的面积=4S△ABO=4××3×4=24.
已知a+b=4,ab=3,求a2+b2的值.
解∵a+b=4,∴(a+b)2=42,即a2+2ab+b2=16.
∵ab=3,∴a2+b2=(a+b)2-2ab=10
第8题图
第7题图
数 学 试 题
注意事项:
1.本试卷共6页,满分120分,考试时间100分钟。
2.试题卷上不要答题,请用0.5毫米黑色签字水笔直接把答案写在答题卡上。答在试题卷上的答案无效。
3.答题前,考生务必将本人姓名、准考证号填写在答题卡第一面的指定位置上。
一、选择题(每小题3分,共30分)
1.数据:,,,,其中是无理数的是
A. B. C. D.
2.下列运算正确的是
A. B.
C. D.
3.已知△ABC中,,求证:,下面写出运用反证法证明这个命题的四个步骤:
①∴,这与三角形内角和为矛盾
②因此假设不成立.∴
③假设在△ABC中,
④由,得,即.
这四个步骤正确的顺序应是
A.④③①② B.③④②① C.①②③④ D.③④①②
4.有下列条件不能判断△ABC是直角三角形的是
A. B.
C. D.
5.如图,四边形ABCD是一个长方形,利用不同的方法可以计算出长方形的面积.通过分析图形中所标线段的长度,将多项式因式分解,其结果正确的是
A. B. C. D.
第5题图 第7题图
6.如图,下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图,根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中,正确的是
A.甲比乙大 B.甲比乙小
C.甲和乙一样大 D.甲和乙无法比较
7.如图,经过直线AB外一点C作这条直线的垂线,作法如下:
任意取一点K,使点K和点C在AB的两旁;
以点C为圆心,CK长为半径作弧,交AB与点D和E;
分别以点D和点E为圆心,大于的长为半径作弧,两弧相交与点F;
作直线CF;
则直线CF就是所求作的垂线,根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为
A.△CDF B.△CDK C.△CDF D.△DEF
8.已知a,b是等腰三角形的两边长,且a,b满足,则此等腰三角形的周长为
A.7 B.8 C.7或8 D.9
9.如图,在△ABC中,,点E为边AC的中点,DE⊥AC,交BC于点D,若AB=5,BC=13,则BD的长为
A.5 B.6 C.7 D.8
第9题图 第10题图
10.如图,桌上有一个圆柱形玻璃杯(无盖)高6厘米,底面周长16厘米,在杯口内壁离杯口1.5厘米的A处有一滴蜜糖,在玻璃杯的外壁,A的相对方向有一小虫P,小虫离杯底的垂直距离为1.5厘米,小虫爬到蜜糖处的最短距离是
A.厘米 B.10厘米 C.厘米 D.8厘米
二、填空题(每小题3分,共15分)
11.9的平方根是 .
12.某市从参加数学质量检测的全体学生中,随机抽取了部分学生的成绩作为研究对象,结果如表所示:
分数段 0~60 60~72 72~84 84~96 96~108 108~120
人数(人) 5 8 30 32 15
百分比 20% 40%
则被抽取的学生人数是_________人.
13.若,,则值为__________.
14.在中,,,.现将△ABC按如图那样折叠,使点A与点B重合,折痕为,则的长是
第14题图 第15题图
15.如图,在边长为6的正方形ABCD内作,AE交BC于点E,AF交CD于点F,连接EF,将△ADF绕点A顺时针旋转90°得到△ABG,若DF=3,则的长为__________.
三、解答题(共75分)
16.(每小题5分,共15分)
(1)计算:
(2)化简:
(3)因式分解:
17.(7分)尺规作图是理论上接近完美的作图方式,乐乐很喜欢用尺规画出要求的图形.在下面的△ABC中,请你也按要求用尺规作出下列图形,并在图中标明相应的字母.(保留作图痕迹,不要求写作法)
(1)作出的角平分线交BC边于点D;
(2)作出AC边上的垂直平分线交AD于点G;
(3)连接GC,若,,则的度数__________.
18.(8分)某校为了检查体育锻炼的效果,抽取部分学生进行模拟测试[模拟成绩分为40分,50分、60分、70分四个等级(满分70分)],相关人员依据测试结果绘制如下两幅尚不完整的统计图,请根据图表解答下列问题:
(1)本次参与模拟测试的学生人数为___________;
(2)扇形统计图中“60分”所对的扇形的圆心角为__________,补全条形统计图;
(3)若将60分及以上的分数定为优秀级别,请你估算1200名学生中达到优秀级别的人数.
19.(7分)数学综合实验课上,同学们在测量学校旗杆高度时发现:将旗杆顶端升旗用的绳子垂到地面还多2米;当把绳子的下端拉开拉直后,下端刚好接触地面,测得绳子的下端离开旗杆底端8米,如图,根据以上数据,同学们就可以准确求出了旗杆的高度,你知道他们是如何计算出来的吗 请你写出计算过程.
20.(9分)如图,在Rt△ABC中,∠ACB=90°,CA=CB,点D是AB上一点,连接CD,作等腰Rt△DCE,且∠DCE=90°,连接AE.
(1)求证:△CEA≌△CDB;
(2)求证:BD2+AD2=DE2.
21.(9分)阅读理解:完全平方公式适当的变形,可以解决很多的数学问题.
根据上面的解题思路与方法,解决下列问题:
(1)若x-y=-3,xy=-2,则x2+y2=____________,(x+y)2=____________;
(2)若m+n-p=-10,(m-p)n=-12. 求(m-p)2+n2的值;
(3)若a2+ab+b2=10,a2-ab+b2=4,则a-b=____________.
22.(10分)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点P从点A出发,以每秒2个单位长度的速度沿折线A—C—B—A运动.设点P的运动时间为t秒(t>0).
(1)求AC的长及斜边AB上的高;
(2)若点P在∠BAC的角平分线上,则t的值为_________.
(3)在整个运动中,直接写出△BCP是以BC为腰的等腰三角形时t的值.
23.(10分)(1)【阅读验证】公元前6世纪,古希腊数学家毕达哥拉斯发现了直角三角形的三边之间的数量关系:在直角三角形中,两条直角边的平方和等于__________,这个结论在中国称之为“勾股定理”.
我国三国时期的数学家赵爽利用四个全等的直角三角形拼成如图1的“弦图”(史称“赵爽弦图”),其中四边形ABDE和四边形CFGH都是正方形,巧妙地用面积法给出了勾股定理的证明过程:
已知:Rt△ABC中,∠ACB=90°.AC=b,BC=a,AB=c.
求证:a2+b2=c2
证明:由图可知S正方形ABDE=4S△ABC+S正方形FCHG
∵S正方形ABDE=c2,S△ABC=ab,正方形FCHG边长为(a-b),
∴
即.
(2)【操作发现】如图2,将等腰直角三角板ABD顶点A放在直线l上,过点B作BC⊥l,过点D作DE⊥l,垂足分别为C、E.
①求证:CE=BC+DE;
②聪聪认真观察图2后发现:如果设AC=b,BC=a,AB=c,此图也可以利用面积法证明勾股定理.请你帮聪聪完成证明过程.
(3)【拓展应用】
如图3,将图1中的这四个直角三角形紧密地拼接,形成飞镖状,已知外围轮廓(粗线)的周长为24,OC=3,直接写出该飞镖状图案的面积.
2022年秋期期终阶段性文化素质监测八年级
数学试题参考答案及评分细则
一、选择题(每小题3分,共30分)
1.C 2.D 3.D 4.A 5.B 6.A 7.C 8.C 9.D 10.B
10.把圆柱沿着点A所在母线展开,如图所示,作点A的对称点B,连接PB,则PB为所求,根据题意,得PC=8,BC=6,根据勾股定理,得PB=10,
二、填空题(每小题3分,共15分)
11.±3 12.150 13.-14 14. 15.2
三、解答题(本大题满分75分)
16.(15分)
解:(1)原式=……………………………2分
……………………………………… .5分
解:(2)
………………………………………………2分
…………………………………………………………………4分
=4x-6y.……………………………………………………………………………………5分
解:(3)
…………………………………………………………………………2分
……………………………………………………………………………5分
17.(7分)(1)解:作的角平分线交BC边于点D,如图所示,
如图所示,是的角平分线,交于点.……………………………2分
(2)作边上的垂直平分线交于点,如图所示,
如图所示,是边上的垂直平分线.………………………………………………4分
(3).………………………………………………………………………………7分
18.(8分)(1)20;……………………………………………………………2分
(2)144°,……………………………………………………………………………4分
图见详解; 条形图如下:
………………………………………5分
(3)解:根据题意,60分所占的百分比为;,……………6分
1200名学生中达到优秀级别的人数为:
(人);……………………………………………………8分
19. (7分)解:设旗杆高米,则绳子长为米,…………………………1分
∵旗杆垂直于地面,
∴旗杆,绳子与地面构成直角三角形,
在Rt△ABC中,,
∴,……………………………………………………………4分
解方程得:,…………………………………………………7分
答:旗杆高度为15米.
20.(9分)
(1)∵△ABC和△DCE都是等腰直角三角形,
∴AC=BC,CD=EC,∠ACB=∠DCE=90°,………………………………………2分
∴∠ACB-∠ACD=∠DCE-∠ACD,
∴∠ACE=∠BCD,
在△CDB与△CEA中,
……………………………………………………………4分
∴△CDB≌△CEA.…………………………………………………………5分
(2)∵△ABC是等腰直角三角形,
∴∠B=∠BAC=45°,………………………………………………………………6分
由(1)得△CDB≌△CEA,
∴∠EAC=∠B=45°,BD=AE,
∴∠EAD=∠EAC+∠BAC=45°+45°=90°,………………………………………8分
∴AE2+AD2=DE2,
∴BD2+AD2=DE2.………………………………………………………………9分
21.(9分)(1)5,1 ………………………………………………(每空2分)4分
(2)解:∵m+n-p=-10,(m-p)=-12,
即(m-p)+n=-10,(m-p)n=-12,
∴(m-p)2+n2=[(m-p)+n]2-2(m-p)n………………5分
=(-10)2-2×(-12)=124;……………………………………………………7分
(3)±1 …………………………………………………………………………9分
22.(10分)(1)在△ABC中,∠ACB=90°,AB=5,BC=3,
由勾股定理得:AC==4.……………………………2分
设斜边AB上的高为h,
∵AB hAC BC,…………………………………………………3分
∴5h=3×4,
∴h=2.4.………………………………………………………………………4分
∴AC的长为4,斜边AB上的高为2.4;
…………………………………………………………………7分
(3)t的值为0.5或5或5.3…………………………(每写对一个1分)10分
(2)已知点P从点A出发,以每秒2个单位长度的速度沿折线A﹣C﹣B﹣A运动,
当点P'在∠BAC的角平分线上时,过点P'作P'D⊥AB,如图:
∵AP'平分∠BAC,P'C⊥AC,P'D⊥AB,
∴P'D=P'C=2t﹣4,
∵BC=3,
∴BP'=3﹣(2t﹣4)=7﹣2t,
在Rt△ACP'和Rt△ADP'中,
∴Rt△ACP'≌Rt△ADP'(HL),
∴AD=AC=4,
又∵AB=5,
∴BD=1,
在Rt△BDP'中,由勾股定理得:
12+(2t﹣4)2=(7﹣2t)2,
解得:t.
故答案为:.
(3)由图可知,当△BCP是等腰三角形时,点P必在线段AC或线段AB上,
①当点P在线段AC上时,此时△BCP是等腰直角三角形,
∴此时CP=BC=3,
∴AP=AC﹣CP=4﹣3=1,
∴2t=1,
∴t=0.5;
②当点P在线段AB上时,若BC=BP,
则点P运动的长度为:
AC+BC+BP=4+3+3=10,
∴2t=10,
∴t=5;
若PC=BC,如图2,过点C作CH⊥AB于点H,则BP=2BH,
在△ABC中,∠ACB=90°,AB=5,BC=3,AC=4,
∴AB CH=AC BC,
∴5CH=4×3,
∴CH,
在Rt△BCH中,由勾股定理得:
BH1.8,
∴BP=3.6,
∴点P运动的长度为:AC+BC+BP=4+3+3.6=10.6,
∴2t=10.6,
∴t=5.3;
综上,t的值为0.5或5或5.3.
23.(10分)(1)斜边的平方;……………………………………………………1分
(2)①证明:在等腰直角三角板ABD中
由已知得AD=AB,∠BAD=90°
∴∠BAC+∠DAE=90°
又∵BC⊥l,DE⊥l
∴∠BCA=∠DEA=90°,∠BAC+∠ABC=90°
∴∠DAE=∠ABC………………………………………………………………2分
∴Rt△ABC≌Rt△DAEAAS)…………………………………………………3分
∴BC=AE,AC=DE…………………………………………………4分
又∵CE=AC+AE
∴CE=BC+DE.……………………………………………………………5分
②解:由上可知BC=AE=a,AC=DE=b
∴S梯形BCED=(BC+DE)×CE=(a+b)2=a2+ab+b2……………………6分
又∵S梯形BCED=S△ABC+S△ABD+S△ADE=ab+c2+ab
∴a2+ab+b2=ab+c2+ab………………………………………………7分
整理得a2+b2=c2 ………………………………………………………8分
(3)飞镖状图案的面积为24.……………………………………………10分
解:∵飞镖模型的周长为24,观察可知4(AB+AC)=24
∴AB+AC=6
∵OB=OC
∴AB=5,OB=3,OA=4
∴飞镖状图案的面积=4S△ABO=4××3×4=24.
已知a+b=4,ab=3,求a2+b2的值.
解∵a+b=4,∴(a+b)2=42,即a2+2ab+b2=16.
∵ab=3,∴a2+b2=(a+b)2-2ab=10
第8题图
第7题图
同课章节目录
