有理数乘法
图片预览



文档简介
课件18张PPT。有理数的乘法情境引入1、计算:(1)(-2)+(-2)
(1)(-2)+(-2)+(-2)
(3)(-2)+(-2)+(-2)+(-2)
(4)(-2)+(-2)+(-2)+(-2)+(-2)2、猜想下列各式的值:
(1)(-2)×2
(2)(-2)×3
(3)(-2)×4
(4)(-2)×5两个有理数的相乘还有哪些情况?=-4=-6=-10=-8=-10=-8=-6=-4实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好
在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
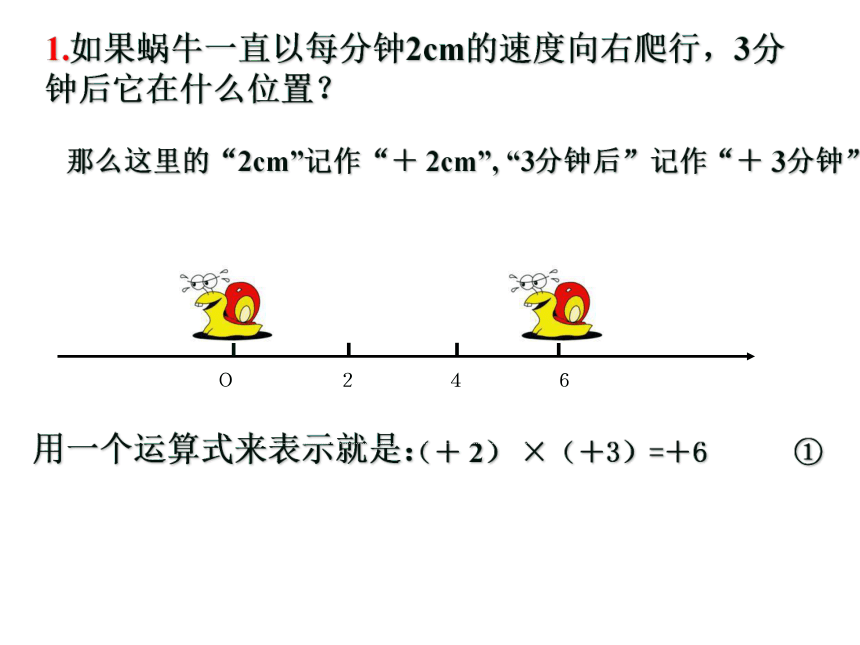
3分钟前它在什么位置?OL探究1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分
钟后它在什么位置?那么这里的“2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”
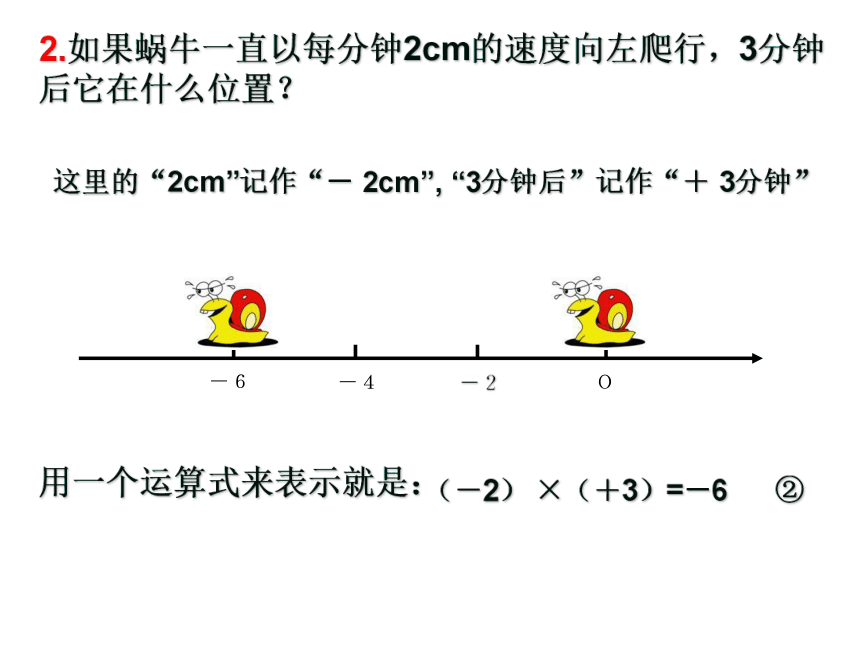
用一个运算式来表示就是:(+ 2) ×(+3)=+6 ①2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
这里的“2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:
(-2) ×(+3)=-6 ②
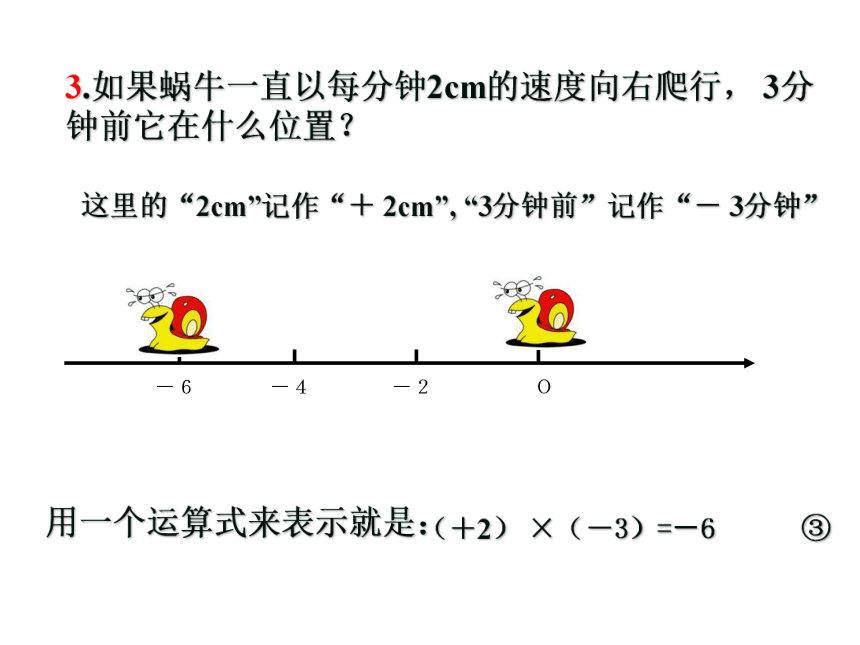
3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分
钟前它在什么位置?这里的“2cm”记作“+ 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)=-6 ③
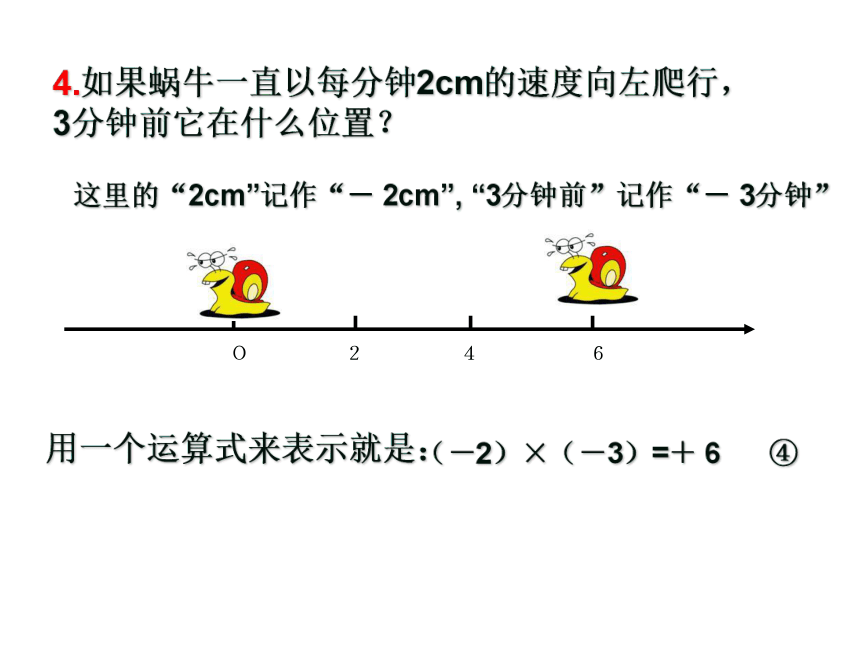
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
这里的“2cm”记作“- 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:(-2)×(-3)=+ 6 ④
由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
正正负负积总结:请同学们观察①~④这四个式子,完成下面的填空:
正数乘正数积为 数。
负数乘正数积为 数。
正数乘负数积为 数。
负数乘负数积为 数。
乘积的绝对值等于各乘数绝对值的归纳:两数相乘,同号得正,异号得负,并把绝对值相乘。此外,我们还知道2 ×0 = 0 ,那么 -2 ×0 = ?显然, -2 ×0 = 0
也就是:任何数同零相乘,都得零。有理数的乘法法则有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。例如:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= + 15
异号两数相乘得负把绝对值相乘 进行有理数的乘法运算关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,在确定积的符号时要准确运用法则;
第二步:求绝对值的积。思考:例1、 (1) (-3) ×9 (2) (-4) ×(-5)
(5)- 2.4 ×0乘积是1的两个数互为倒数。解:=-27=1=1==0201.口答:
(1)6×(-9); (2)(-6)×(-9);
(3)(-6)×9; (4)(-6)×1;
(5)(-6)×(-1); (6) 6×(-1);
(7)(-6)×0; (8)0×(-6); =-54=54=6=-6=0=-6=0=-1.5=-54=4=-=- 4.填空
(1)1×(-6)=______;(2)1+(-6)=_______;
(3)(-1)×6=________;(4)(-1)+6=______;
(5)(-1)×(-6)=______;(6)(-1)+(-6)=_____ 总结:一个数乘以1都等于它本身; 一个数乘以-1都等于它的相反数. -6-5-656-7例2 、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3=-18答:气温下降了18℃.例2 判断题(对的入“T”,错的入“F”)
(1) 同号两数相乘,符号不变. ( )
(2) 异号两数相乘,取绝对值较大的因数的符号( )
(3) 两数相乘,如果积为正数,则这两个因数都为正数( )
(4) 两数相乘,如果积为负数,则这两个因数异号( )
(5) 两数相乘,如果积为0,则这两个数全为0.( )
(6) 两个数相乘,积比每一个因数都大.( )
(7) 如果ab>0,且a+b<0,则a<0,b<0. ( )
(8) 如果ab<0,则a>0,b<0. ( )
(9) 如果ab=0,则a,b中至少有一个为0. ( )FFF TF F TFT用“<”或“>”号填空:
(1)如果a<0 b>0那么 ab _ 0
(2)如果a<0 b<0那么 ab _ 0<>1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。 2. 倒数的定义1.作业:习题1.4 第1、2题;
2.《练习册》和《十分钟掌控课堂》小结:乘积是1的两个数互为倒数。再见谢谢大家
(1)(-2)+(-2)+(-2)
(3)(-2)+(-2)+(-2)+(-2)
(4)(-2)+(-2)+(-2)+(-2)+(-2)2、猜想下列各式的值:
(1)(-2)×2
(2)(-2)×3
(3)(-2)×4
(4)(-2)×5两个有理数的相乘还有哪些情况?=-4=-6=-10=-8=-10=-8=-6=-4实例:如下图所示,一只蜗牛沿直线L爬行,它的位置恰好
在L上的O点。
1.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟后它在什么位置?
2.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟后它在什么位置?
3.如果蜗牛一直以每分钟2cm的速度向右爬行,
3分钟前它在什么位置?
4.如果蜗牛一直以每分钟2cm的速度向左爬行,
3分钟前它在什么位置?OL探究1.如果蜗牛一直以每分钟2cm的速度向右爬行,3分
钟后它在什么位置?那么这里的“2cm”记作“+ 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:(+ 2) ×(+3)=+6 ①2.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟后它在什么位置?
这里的“2cm”记作“- 2cm”, “3分钟后”记作“+ 3分钟”
用一个运算式来表示就是:
(-2) ×(+3)=-6 ②
3.如果蜗牛一直以每分钟2cm的速度向右爬行, 3分
钟前它在什么位置?这里的“2cm”记作“+ 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:
(+2) ×(-3)=-6 ③
4.如果蜗牛一直以每分钟2cm的速度向左爬行,3分钟前它在什么位置?
这里的“2cm”记作“- 2cm”, “3分钟前”记作“- 3分钟”
用一个运算式来表示就是:(-2)×(-3)=+ 6 ④
由刚才的这四个问题我们就得到了下面四个算术式:
(+ 2) ×(+ 3)= + 6 ①
(- 2) ×(+ 3)= - 6 ②
(+ 2) ×(- 3)= - 6 ③
(-2 ) ×(- 3)= + 6 ④
正正负负积总结:请同学们观察①~④这四个式子,完成下面的填空:
正数乘正数积为 数。
负数乘正数积为 数。
正数乘负数积为 数。
负数乘负数积为 数。
乘积的绝对值等于各乘数绝对值的归纳:两数相乘,同号得正,异号得负,并把绝对值相乘。此外,我们还知道2 ×0 = 0 ,那么 -2 ×0 = ?显然, -2 ×0 = 0
也就是:任何数同零相乘,都得零。有理数的乘法法则有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。
任何数同0相乘,都得0。例如:(-5) ×( -3)………… 同号两数相乘 (-5) ×( -3)= +( ) ,………… 得正 5 × 3 = 15 ,
………… 把绝对值相乘所以:(-5) ×( -3)= + 15
异号两数相乘得负把绝对值相乘 进行有理数的乘法运算关键是积的符号的确定,计算时分两步进行。
第一步:确定积的符号,在确定积的符号时要准确运用法则;
第二步:求绝对值的积。思考:例1、 (1) (-3) ×9 (2) (-4) ×(-5)
(5)- 2.4 ×0乘积是1的两个数互为倒数。解:=-27=1=1==0201.口答:
(1)6×(-9); (2)(-6)×(-9);
(3)(-6)×9; (4)(-6)×1;
(5)(-6)×(-1); (6) 6×(-1);
(7)(-6)×0; (8)0×(-6); =-54=54=6=-6=0=-6=0=-1.5=-54=4=-=- 4.填空
(1)1×(-6)=______;(2)1+(-6)=_______;
(3)(-1)×6=________;(4)(-1)+6=______;
(5)(-1)×(-6)=______;(6)(-1)+(-6)=_____ 总结:一个数乘以1都等于它本身; 一个数乘以-1都等于它的相反数. -6-5-656-7例2 、用正负数表示气温的变化量,上升为正,下降为负.登山队攀登一座山峰,每登高1km气温的变化量为-6℃,攀登3km后,气温有什么变化?解: (-6)×3=-18答:气温下降了18℃.例2 判断题(对的入“T”,错的入“F”)
(1) 同号两数相乘,符号不变. ( )
(2) 异号两数相乘,取绝对值较大的因数的符号( )
(3) 两数相乘,如果积为正数,则这两个因数都为正数( )
(4) 两数相乘,如果积为负数,则这两个因数异号( )
(5) 两数相乘,如果积为0,则这两个数全为0.( )
(6) 两个数相乘,积比每一个因数都大.( )
(7) 如果ab>0,且a+b<0,则a<0,b<0. ( )
(8) 如果ab<0,则a>0,b<0. ( )
(9) 如果ab=0,则a,b中至少有一个为0. ( )FFF TF F TFT用“<”或“>”号填空:
(1)如果a<0 b>0那么 ab _ 0
(2)如果a<0 b<0那么 ab _ 0<>1.有理数的乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘。任何数同0相乘,都得0。 2. 倒数的定义1.作业:习题1.4 第1、2题;
2.《练习册》和《十分钟掌控课堂》小结:乘积是1的两个数互为倒数。再见谢谢大家
