对数的运算性质课件
图片预览



文档简介
课件17张PPT。对数的运算性质 1)对数的定义: ,请同学们回顾一下上节课我们所学习的内容。一般地,如果 的b次幂等于N, 就是 ,那么数 b叫做以a为底 N的对数,记作 . 2)指数式与对数式的互化
3)重要结论用公式
①负数与零没有对数;②
③对数恒等式
,指数的运算性质:
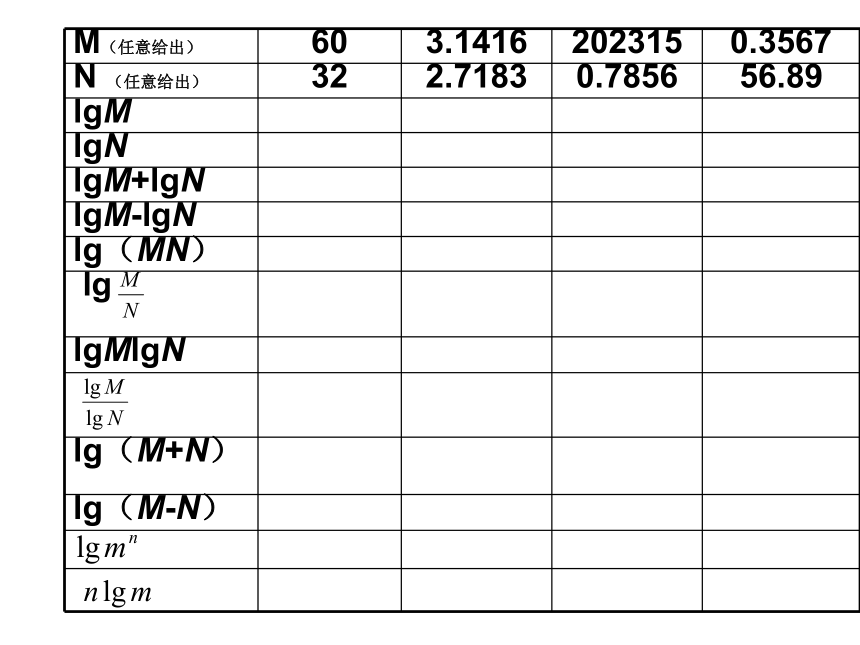
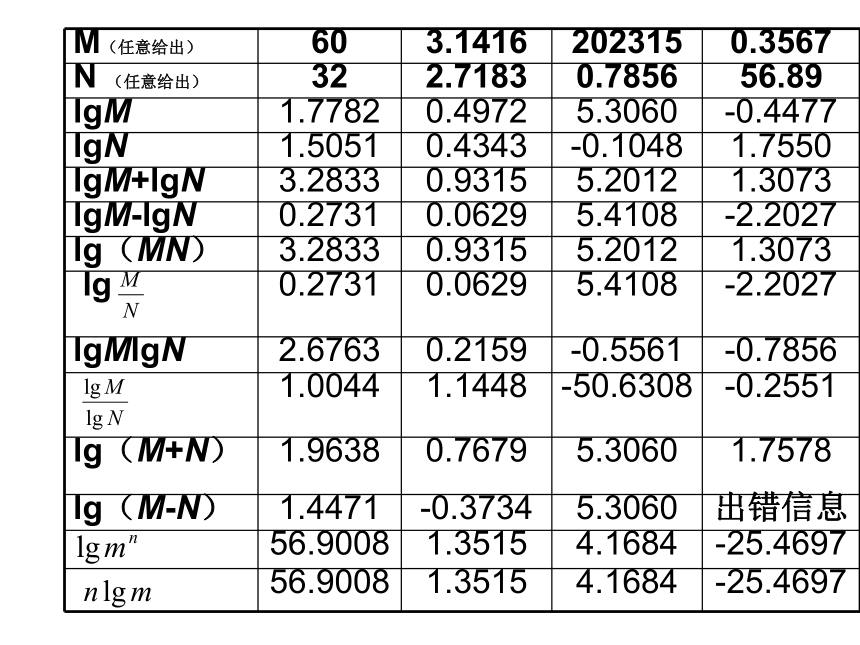
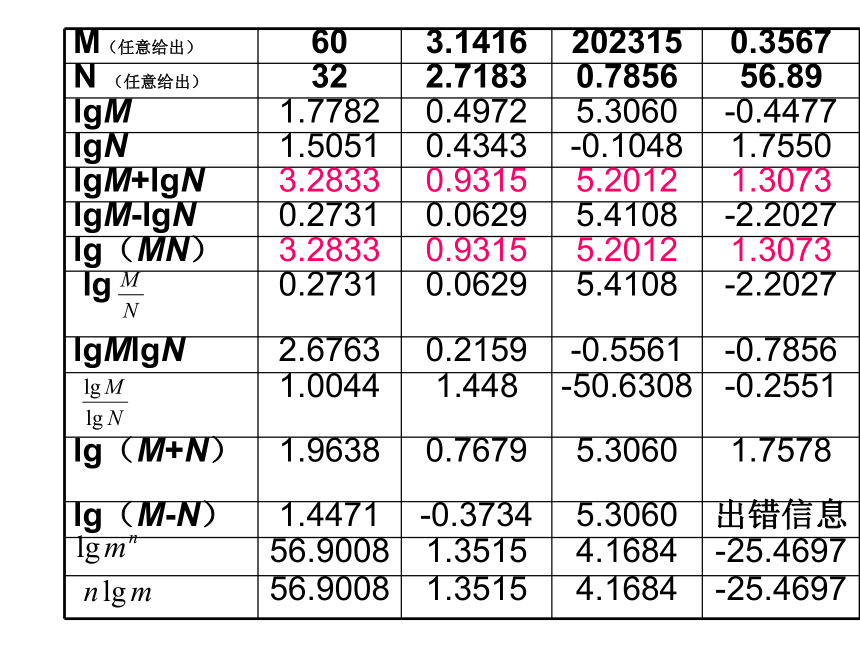
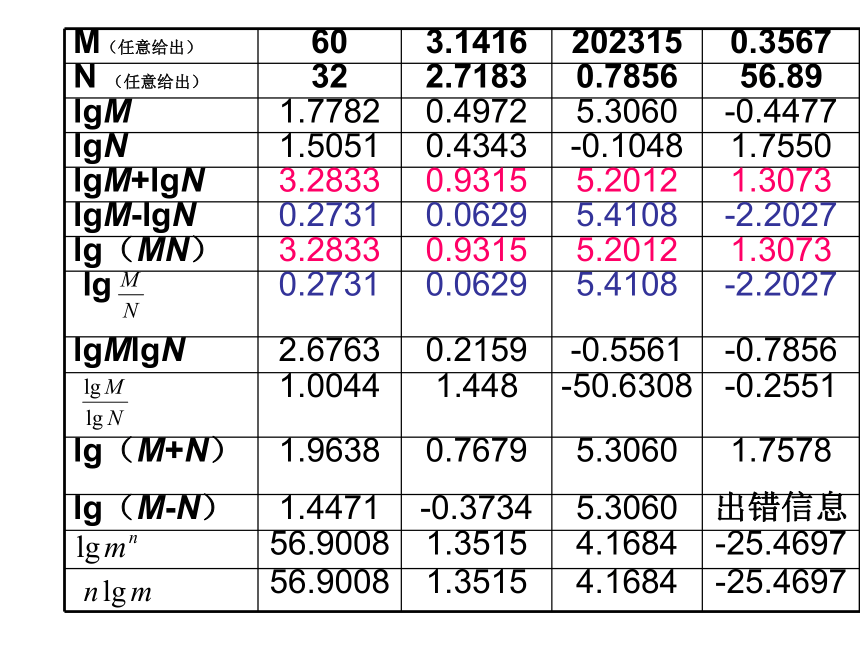
对数的运算性质两个正数的积的对数等于这两个正数的对数和两个正数的商的对数等于这两个正数的对数差语言表达:一个正数的n次方的对数等于这个正数的对数n倍如果 a > 0,a ? 1,M > 0, N > 0 有:证明:②设 由对数的定义可以得: ∴ 即证得 证明:证明:设 由对数的定义可以得: ∴即证得 证明:对数运算公式几个注意点:1) 简易语言表达:“积的对数=对数的和”……
2)真数的取值必须是(0,+∞)
3)有时公式可以可逆
4)
5)≠≠≠例1 计算(1) (2) 讲解范例 解 :=5+14=19解 :例2 计算(1) (2) 解 (1)(2)原式=法二:原式=练习 (1) (4) (3) (2) 1.求下列各式的值:2. 用lgx,lgy,lgz表示下列各式:练习 (1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz;
3)重要结论用公式
①负数与零没有对数;②
③对数恒等式
,指数的运算性质:
对数的运算性质两个正数的积的对数等于这两个正数的对数和两个正数的商的对数等于这两个正数的对数差语言表达:一个正数的n次方的对数等于这个正数的对数n倍如果 a > 0,a ? 1,M > 0, N > 0 有:证明:②设 由对数的定义可以得: ∴ 即证得 证明:证明:设 由对数的定义可以得: ∴即证得 证明:对数运算公式几个注意点:1) 简易语言表达:“积的对数=对数的和”……
2)真数的取值必须是(0,+∞)
3)有时公式可以可逆
4)
5)≠≠≠例1 计算(1) (2) 讲解范例 解 :=5+14=19解 :例2 计算(1) (2) 解 (1)(2)原式=法二:原式=练习 (1) (4) (3) (2) 1.求下列各式的值:2. 用lgx,lgy,lgz表示下列各式:练习 (1) (4) (3) (2) =lgx+2lgy-lgz;=lgx+lgy+lgz;=lgx+3lgy- lgz;
