安徽省合肥市蜀山区2023-2024年度九年级上学期数学期末复习卷一(含答案)
文档属性
| 名称 | 安徽省合肥市蜀山区2023-2024年度九年级上学期数学期末复习卷一(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 594.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 16:40:40 | ||
图片预览




文档简介
2023-2024年度合肥市蜀山区九年级上学期数学期末复习卷
考试范围:九年级上册全书,下册第二十四章
姓名: 学号: 考号: 分数: 。
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
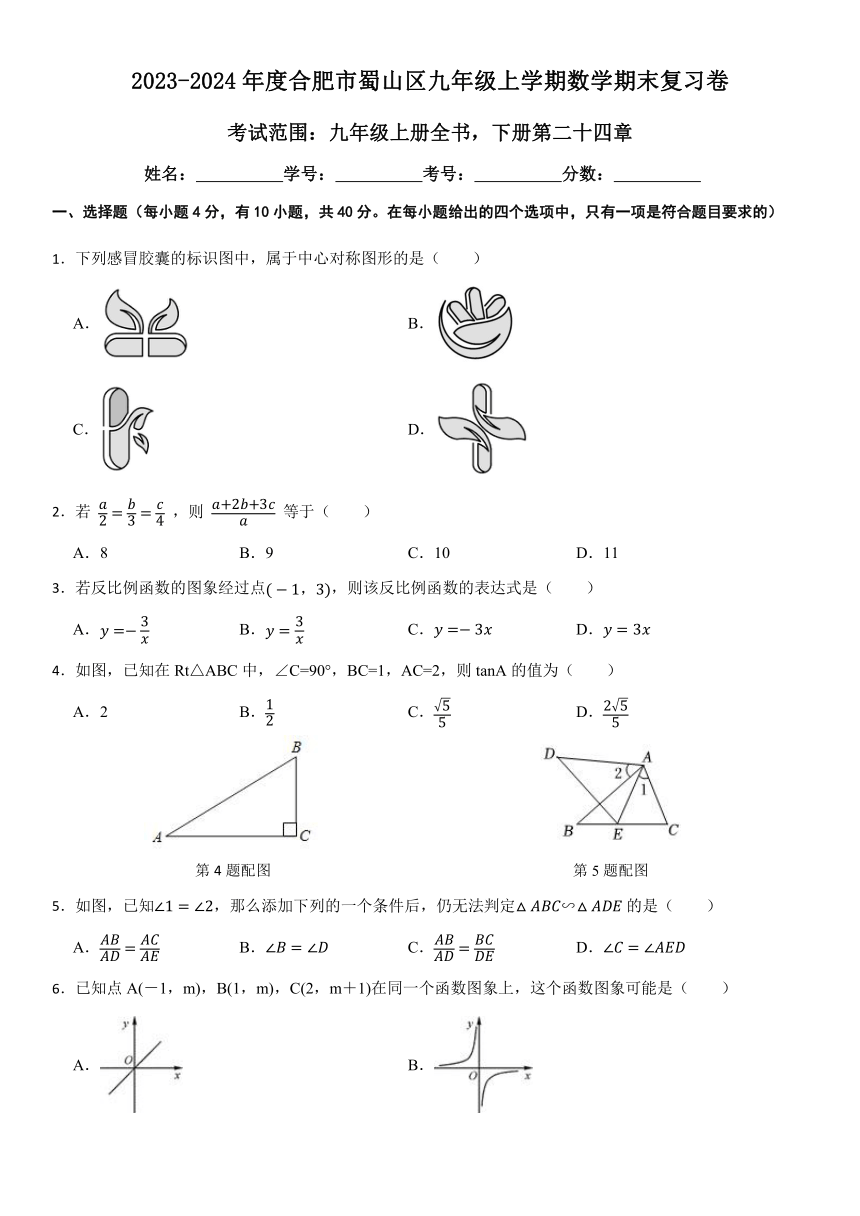
1.下列感冒胶囊的标识图中,属于中心对称图形的是( )
A. B.
C. D.
2.若 ,则 等于( )
A.8 B.9 C.10 D.11
3.若反比例函数的图象经过点,则该反比例函数的表达式是( )
A. B. C. D.
4.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
A.2 B. C. D.
第4题配图 第5题配图
5.如图,已知,那么添加下列的一个条件后,仍无法判定∽的是( )
A. B. C. D.
6.已知点A(-1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可能是( )
A. B.
C. D.
7.如图, 、 是 的切线, 、 为切点,点 在 上,且 ,则 的度数为( )
A.55° B.65° C.70° D.90°
8.已知一圆锥的母线长为6,底面半径为3,则该圆锥的侧面积为( )
A.27π B.36π C.18π D.9π
9.如图,四边形内接于,交的延长线于点E,若平分,,,则( )
A.3 B. C. D.
10. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( )
A. B.2 C. D.
二、填空题(每小题5分,共4小题,共20分)
11.已知线段 , ,则 , 的比例中项线段为 .
12.如图,为的直径,弦,垂足为,,,,则弦的长度为 .
第12题配图 第13题配图 第14题配图
13.如图,在等腰直角三角形中,,点P在以斜边为直径的半圆上,M为的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是 .
14.已知点是反比例函数图象上的动点,轴,轴,分别交反比例函数的图象于点B、C,交坐标轴于D、E,且,连接.现有以下四个结论:①;②在点A运动过程中,的面积始终不变;③连接,则;④不存在点A,使得.其中正确的结论的序号是 .
三、解答题(共9小题,15-18题每题8分,19-20题每题10分,21-22题每题12分,23题14分共90分。解答应写出文字说明、证明过程或演算步骤)
15.计算:
16.如图,在网格图中(小正方形的边长为1),△ABC的三个顶点都在格点上.
把△ABC沿着x轴向右平移6个单位得到△A1B1C1,请画出△A1B1C1;
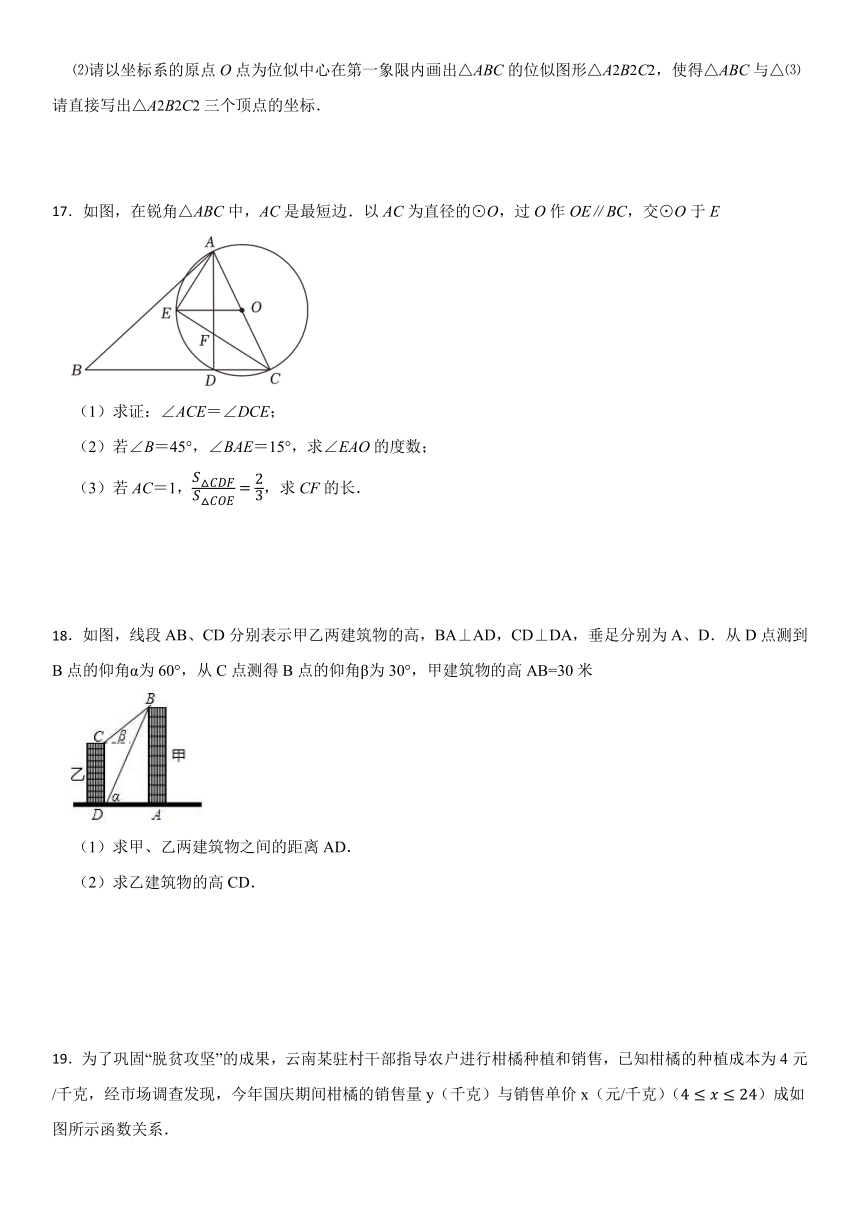
⑵请以坐标系的原点O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△⑶请直接写出△A2B2C2三个顶点的坐标.
17.如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,过O作OE∥BC,交⊙O于E
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
18.如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
19.为了巩固“脱贫攻坚”的成果,云南某驻村干部指导农户进行柑橘种植和销售,已知柑橘的种植成本为4元/千克,经市场调查发现,今年国庆期间柑橘的销售量y(千克)与销售单价x(元/千克)()成如图所示函数关系.
(1)根据函数图象提供的信息,求y与x的函数关系式;
(2)若国庆期间销售柑橘获取的利润W元,求出销售单价定为多少元时,获得的利润最大?最大利润是多少?
20.如图,在和中,,.
(1)求证:;
(2)若,,求的长.
21.如图,以矩形ABCD的边CD为直径作,点E是AB的中点,连接CE交于点F,连接AF并延长交BC于点H.
(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是的切线;
(3)若,,求AH的长.
22.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线经过,两点,与轴的另一个交点为点.
(1)求抛物线的函数表达式.
(2)点为直线上方抛物线上一动点,连接,,设直线交线段于点,的面积为,的面积为,求的最大值.
23.如图(1),在直角三角形中,,,.,点是边上的动点,作,交于点,与相交于点.
(1)求证:.
(2)如图2,将沿翻折,点落在处,直线交于点.
①当时,求的长.
②当时,求的长.
2023-2024年度合肥市蜀山区九年级上学期数学期末复习卷参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】6
12.【答案】
13.【答案】
14.【答案】①②③
15.【答案】解:原式=
16.【答案】解:⑴如图,△A1B1C1为所作;
⑵如图,△A2B2C2为所作;
⑶△A2B2C2三个顶点的坐标分别为A2(6,0),B2(6,4),C2(2,6).
17.【答案】(1)证明:∵OC=OE,
∴∠OEC=∠OCE,
∵OE∥BC,
∴∠OEC=∠ECD,
∴∠OCE=∠ECD,
即∠ACE=∠DCE,
(2)解:延长AE交BC于点G,
∵∠AGC是△ABG的外角,
∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,
∴∠AEO=∠AGC=60°,
∵OA=OE,
∴∠EAO=∠AEO=60°;
(3)解:∵O是AC中点
∴,
∵,
∴,
∵AC是直径,
∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,
∴△CDF∽△CEA,
∴=,
∴CF=.
18.【答案】(1)解:作CE⊥AB于点E,
在Rt△ABD中,AD= = =10 (米);
(2)解:在Rt△BCE中,CE=AD=10 米,
BE=CE tanβ=10 × =10(米),
则CD=AE=AB﹣BE=30﹣10=20(米)
答:乙建筑物的高度DC为20m.
19.【答案】(1)解:由图象可知y与x之间的关系式为:,代入,可得:
,解得:,
∴y与x之间的函数关系式为:;()
(2)解:由题意可得:,
∴当时,W的最大值为1536,
答:销售单价定为20元/千克时,获得的利润最大,最大利润为1536元.
20.【答案】(1)证明:∵,
∴,
∴,
∵,
∴.
(2)解:由(1)得,,
∵,
∴,
∵,
∴.
21.【答案】(1)结论:四边形AECO是平行四边形
理由:∵四边形ABCD是矩形
∴,
又,
∴,
∴四边形AECO是平行四边形
(2)解:由(1)得
∴,
又
∴
则又
∴
∴即又OF是的半径
∴是的切线
(3)由切线长定理可设,
且则
在中,
由得得
∴
22.【答案】(1)解:∵直线与x轴交于点A,与y轴交于点C,
∴A(﹣4,0),C(0,2),
∵抛物线经过A,C两点,
∴,
解得.
∴抛物线的解析式为:.
(2)解:令y=0,
∴,
解得x=﹣4或x=1,
∴B(1,0),
如图,过点D作DM⊥x轴交AC于点M,过点B作BN⊥x轴交AC于点N,
∴,
∴,
∴,
∴.
设点D的横坐标为a,
∴,
∴,
∴,
∵B(1,0),
∴,
∴,
∴,
∴当时,的值最大,最大值为.
23.【答案】(1)证明:如图1所中:
∵,
∴.
又∵,,
∴,
∴,
∴,
∴.
(2)解:①如图2中:
∵沿翻折,
∴.
∵,
∴,,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∵,,
∴.
②当点在上方时,如图3中,过点作于,设.
∵沿翻折,
∴,,,.
∵,
∴,
∴,
∴.
∵,
∴四边形是矩形,
∴,,.
∵,
∴,
∴或(舍去),
∴,
当点落在下方时,如图4中,
同法可得,
∴或(舍去),
∴.
∵,
∴此种情形不符合题意,舍去.
综上所述,.
考试范围:九年级上册全书,下册第二十四章
姓名: 学号: 考号: 分数: 。
一、选择题(每小题4分,有10小题,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下列感冒胶囊的标识图中,属于中心对称图形的是( )
A. B.
C. D.
2.若 ,则 等于( )
A.8 B.9 C.10 D.11
3.若反比例函数的图象经过点,则该反比例函数的表达式是( )
A. B. C. D.
4.如图,已知在Rt△ABC中,∠C=90°,BC=1,AC=2,则tanA的值为( )
A.2 B. C. D.
第4题配图 第5题配图
5.如图,已知,那么添加下列的一个条件后,仍无法判定∽的是( )
A. B. C. D.
6.已知点A(-1,m),B(1,m),C(2,m+1)在同一个函数图象上,这个函数图象可能是( )
A. B.
C. D.
7.如图, 、 是 的切线, 、 为切点,点 在 上,且 ,则 的度数为( )
A.55° B.65° C.70° D.90°
8.已知一圆锥的母线长为6,底面半径为3,则该圆锥的侧面积为( )
A.27π B.36π C.18π D.9π
9.如图,四边形内接于,交的延长线于点E,若平分,,,则( )
A.3 B. C. D.
10. 如图,已知二次函数的图象与x轴交于A、B两点(点A在点B的左侧),与轴交于点C,P为该二次函数在第一象限内的一点,连接AP,交BC于点K,则的最小值为( )
A. B.2 C. D.
二、填空题(每小题5分,共4小题,共20分)
11.已知线段 , ,则 , 的比例中项线段为 .
12.如图,为的直径,弦,垂足为,,,,则弦的长度为 .
第12题配图 第13题配图 第14题配图
13.如图,在等腰直角三角形中,,点P在以斜边为直径的半圆上,M为的中点,当点P沿半圆从点A运动至点B时,点M运动的路径长是 .
14.已知点是反比例函数图象上的动点,轴,轴,分别交反比例函数的图象于点B、C,交坐标轴于D、E,且,连接.现有以下四个结论:①;②在点A运动过程中,的面积始终不变;③连接,则;④不存在点A,使得.其中正确的结论的序号是 .
三、解答题(共9小题,15-18题每题8分,19-20题每题10分,21-22题每题12分,23题14分共90分。解答应写出文字说明、证明过程或演算步骤)
15.计算:
16.如图,在网格图中(小正方形的边长为1),△ABC的三个顶点都在格点上.
把△ABC沿着x轴向右平移6个单位得到△A1B1C1,请画出△A1B1C1;
⑵请以坐标系的原点O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2,使得△ABC与△⑶请直接写出△A2B2C2三个顶点的坐标.
17.如图,在锐角△ABC中,AC是最短边.以AC为直径的⊙O,过O作OE∥BC,交⊙O于E
(1)求证:∠ACE=∠DCE;
(2)若∠B=45°,∠BAE=15°,求∠EAO的度数;
(3)若AC=1,,求CF的长.
18.如图,线段AB、CD分别表示甲乙两建筑物的高,BA⊥AD,CD⊥DA,垂足分别为A、D.从D点测到B点的仰角α为60°,从C点测得B点的仰角β为30°,甲建筑物的高AB=30米
(1)求甲、乙两建筑物之间的距离AD.
(2)求乙建筑物的高CD.
19.为了巩固“脱贫攻坚”的成果,云南某驻村干部指导农户进行柑橘种植和销售,已知柑橘的种植成本为4元/千克,经市场调查发现,今年国庆期间柑橘的销售量y(千克)与销售单价x(元/千克)()成如图所示函数关系.
(1)根据函数图象提供的信息,求y与x的函数关系式;
(2)若国庆期间销售柑橘获取的利润W元,求出销售单价定为多少元时,获得的利润最大?最大利润是多少?
20.如图,在和中,,.
(1)求证:;
(2)若,,求的长.
21.如图,以矩形ABCD的边CD为直径作,点E是AB的中点,连接CE交于点F,连接AF并延长交BC于点H.
(1)若连接AO,试判断四边形AECO的形状,并说明理由;
(2)求证:AH是的切线;
(3)若,,求AH的长.
22.如图,在平面直角坐标系中,直线与轴交于点,与轴交于点,抛物线经过,两点,与轴的另一个交点为点.
(1)求抛物线的函数表达式.
(2)点为直线上方抛物线上一动点,连接,,设直线交线段于点,的面积为,的面积为,求的最大值.
23.如图(1),在直角三角形中,,,.,点是边上的动点,作,交于点,与相交于点.
(1)求证:.
(2)如图2,将沿翻折,点落在处,直线交于点.
①当时,求的长.
②当时,求的长.
2023-2024年度合肥市蜀山区九年级上学期数学期末复习卷参考答案
1.【答案】D
2.【答案】C
3.【答案】A
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】C
8.【答案】C
9.【答案】C
10.【答案】A
11.【答案】6
12.【答案】
13.【答案】
14.【答案】①②③
15.【答案】解:原式=
16.【答案】解:⑴如图,△A1B1C1为所作;
⑵如图,△A2B2C2为所作;
⑶△A2B2C2三个顶点的坐标分别为A2(6,0),B2(6,4),C2(2,6).
17.【答案】(1)证明:∵OC=OE,
∴∠OEC=∠OCE,
∵OE∥BC,
∴∠OEC=∠ECD,
∴∠OCE=∠ECD,
即∠ACE=∠DCE,
(2)解:延长AE交BC于点G,
∵∠AGC是△ABG的外角,
∴∠AGC=∠B+∠BAG=60°,
∵OE∥BC,
∴∠AEO=∠AGC=60°,
∵OA=OE,
∴∠EAO=∠AEO=60°;
(3)解:∵O是AC中点
∴,
∵,
∴,
∵AC是直径,
∴∠AEC=∠FDC=90°,
∵∠ACE=∠FCD,
∴△CDF∽△CEA,
∴=,
∴CF=.
18.【答案】(1)解:作CE⊥AB于点E,
在Rt△ABD中,AD= = =10 (米);
(2)解:在Rt△BCE中,CE=AD=10 米,
BE=CE tanβ=10 × =10(米),
则CD=AE=AB﹣BE=30﹣10=20(米)
答:乙建筑物的高度DC为20m.
19.【答案】(1)解:由图象可知y与x之间的关系式为:,代入,可得:
,解得:,
∴y与x之间的函数关系式为:;()
(2)解:由题意可得:,
∴当时,W的最大值为1536,
答:销售单价定为20元/千克时,获得的利润最大,最大利润为1536元.
20.【答案】(1)证明:∵,
∴,
∴,
∵,
∴.
(2)解:由(1)得,,
∵,
∴,
∵,
∴.
21.【答案】(1)结论:四边形AECO是平行四边形
理由:∵四边形ABCD是矩形
∴,
又,
∴,
∴四边形AECO是平行四边形
(2)解:由(1)得
∴,
又
∴
则又
∴
∴即又OF是的半径
∴是的切线
(3)由切线长定理可设,
且则
在中,
由得得
∴
22.【答案】(1)解:∵直线与x轴交于点A,与y轴交于点C,
∴A(﹣4,0),C(0,2),
∵抛物线经过A,C两点,
∴,
解得.
∴抛物线的解析式为:.
(2)解:令y=0,
∴,
解得x=﹣4或x=1,
∴B(1,0),
如图,过点D作DM⊥x轴交AC于点M,过点B作BN⊥x轴交AC于点N,
∴,
∴,
∴,
∴.
设点D的横坐标为a,
∴,
∴,
∴,
∵B(1,0),
∴,
∴,
∴,
∴当时,的值最大,最大值为.
23.【答案】(1)证明:如图1所中:
∵,
∴.
又∵,,
∴,
∴,
∴,
∴.
(2)解:①如图2中:
∵沿翻折,
∴.
∵,
∴,,
∴.
∵,
∴.
∵,
∴.
∵,
∴,
∴.
∵,
∴,
∴,
∵,,
∴.
②当点在上方时,如图3中,过点作于,设.
∵沿翻折,
∴,,,.
∵,
∴,
∴,
∴.
∵,
∴四边形是矩形,
∴,,.
∵,
∴,
∴或(舍去),
∴,
当点落在下方时,如图4中,
同法可得,
∴或(舍去),
∴.
∵,
∴此种情形不符合题意,舍去.
综上所述,.
同课章节目录
