鲁教版(五四制)数学九年级上册 2.6 利用三角函数测高 教案
文档属性
| 名称 | 鲁教版(五四制)数学九年级上册 2.6 利用三角函数测高 教案 |

|
|
| 格式 | doc | ||
| 文件大小 | 733.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 16:33:33 | ||
图片预览


文档简介
利用三角函数测高
【教学目标】
1.能够设计测量方案、说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题。
2.能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果。
3.能够主动积极地想办法,积极地投入到数学活动中去,提高学习数学的兴趣;培养不怕困难的品质,发展合作意识和科学精神。
【教学重点】
综合运用直角三角形边角关系的知识解决实际问题。
【教学难点】
综合运用直角三角形边角关系的知识解决实际问题。
【教学方法】
教师通过设计方案,启发、引导、点拨学生,为学生创设一个自主、合作、探究的学习环境。同时,培养学生的合作意识,开发学生的发散思维能力。渗透认识事物、解决问题的方法,培养学生良好的思维品质。
【教学准备】
每组一个测量倾斜角的仪器(测角仪)、皮尺等测量工具。
【教学过程】
一、探究新知
(一)活动一内容:测量倾斜角
侧倾器的结构:度盘、铅锤和支杆组成。
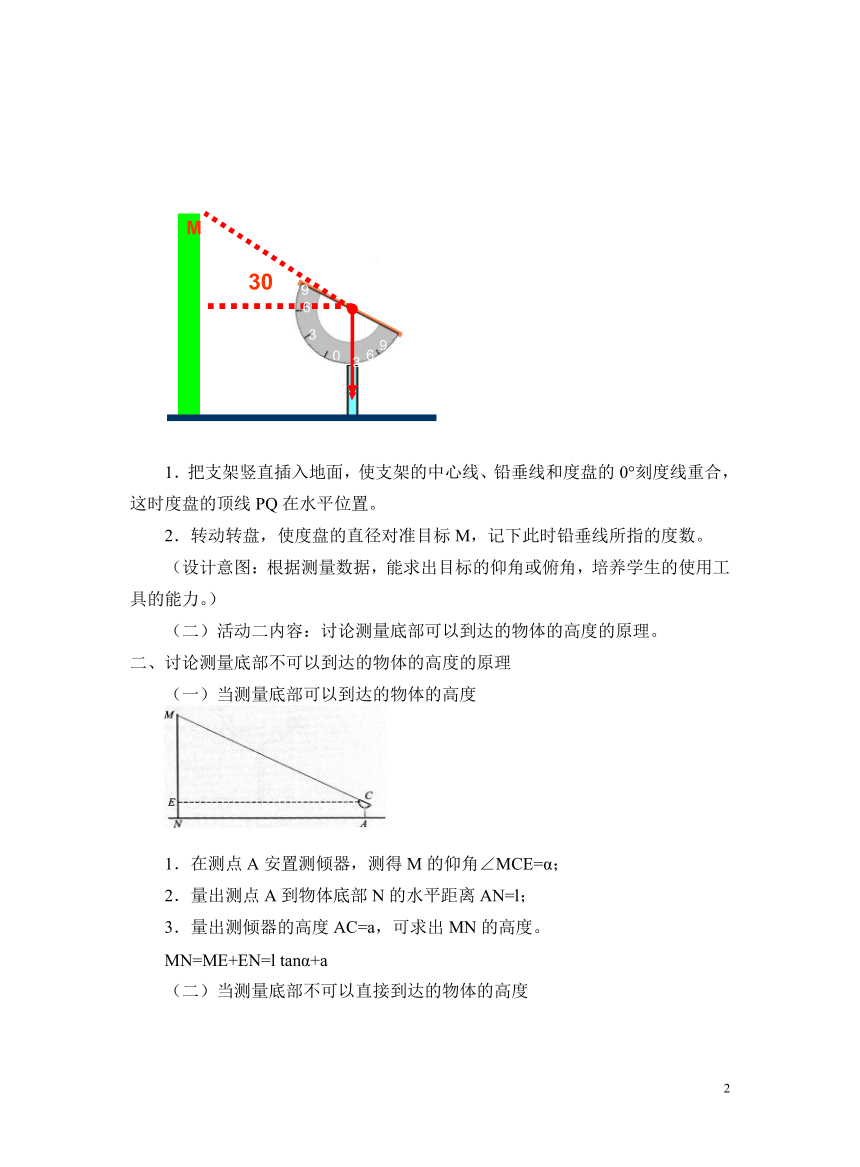
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
(设计意图:根据测量数据,能求出目标的仰角或俯角,培养学生的使用工具的能力。)
(二)活动二内容:讨论测量底部可以到达的物体的高度的原理。
二、讨论测量底部不可以到达的物体的高度的原理
(一)当测量底部可以到达的物体的高度
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度。
MN=ME+EN=l tanα+a
(二)当测量底部不可以直接到达的物体的高度
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2.在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b。根据测量数据,可求出物体MN的高度。
(设计意图:掌握测量的原理 ,提醒学生注意方法的选择;不要忽略了测角仪到地面的高度。培养学生独立设计方案的能力。培养学生科学的思维方式和思维能力。)
三、实验模型
(一)实验1
课题 测量旗杆高
测量示意图
测量项目 AN的长 10.03m 9.97m 平均值:
测倾器的高 CD=1m CD=1m 平均值:
倾斜角 a=29°15′ a=30°45′ 平均值:
计算 旗杆MN的高度(精确到0.1m)
1.请根据测得的数据,填表中的空格;
2.通过计算得旗杆的高为(已知测倾器的高CD=1m)______米(精确到米)。
(二)在Rt△CME中,ME=CEtan30°=1.732,CE=1732
MN=ME+NE=17.32+1=18.32≈18
实验2
课题 在平面上测量地王大厦的高AB
测量示意图
测得数据 测量项目 ∠α ∠β CD的长
第一次 30°16’ 45°35’ 60.11M
第二次 30°44’ 45°25’ 59.89M
平均值
1.请根据测得的数据,填表中的空格;
2.通过计算得地王大厦的高为(已知测倾器的高CE=DF=1m)______米(精确到米)。
(三)在Rt△AEG中,EG=AG/tan30°=1.732AG
在Rt△AFG中,FG=AG/tan45°=AG
FG-EG=CD
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
(设计意图:培养学生动手操作,积极参与数学活动的能力,在活动中体现相互尊重和协调的能力,发展合作意识和科学精神。加深巩固解直角三角形的能力,解决实际问题。)
四、知识运用
例:如图,在某建筑物AC上,挂着“多彩云南”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为,求宣传条幅BC的长(小明的身高不计,结果精确到0.1米)。
解:∵∠BFC =,∠BEC=,∠BCF=
∴∠EBF=∠EBC=
∴BE=EF=20
Rt△BCE
答:宣传条幅BC的长是17.3米。
(设计意图:通过典型例题培养学生独立设计方案和利用三角函数的方法的能力。培养学生科学的思维方式和思维能力。)
五、巩固训练
(一)如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度,标杆与旗杆的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求旗杆的高度。
(二)大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60度,爬到楼顶D测得塔顶B点仰角为30度,求塔BC的高度。
(设计意图:总结数学活动经验,培养学生理论联系实际的能力。)
六、总结串联
本节课通过学习认识侧倾器、达到测量物体的高度的目标你有哪些收获与疑惑?
(设计意图:小结由学生发言,为他们提供一个互相交流的平台,让学生养成反思与总结的习惯,培养学生的语言概括能力。)
七、达标测试
(一)住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=24现了解甲楼对乙楼采光的影响情况。当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?
(二)甲乙两楼之间的距离为40米,小华从甲楼顶测乙楼顶仰角为=30 ,观测乙楼的底部俯角为=45 ,试用含、的三角函数式子表示乙楼的高=______________米。
0
30
30
60
60
90
90
P
Q
M
30°
0
30
30
60
60
90
90
P
Q
M
A
C
N
E
α
D
C
DDDD
C
E
F
A
G
B
α
β
1
【教学目标】
1.能够设计测量方案、说明测量理由,能够综合运用直角三角形边角关系的知识解决实际问题。
2.能对所得数据进行分析,对仪器进行调整和对测量的结果进行矫正,从而得出符合实际的结果。
3.能够主动积极地想办法,积极地投入到数学活动中去,提高学习数学的兴趣;培养不怕困难的品质,发展合作意识和科学精神。
【教学重点】
综合运用直角三角形边角关系的知识解决实际问题。
【教学难点】
综合运用直角三角形边角关系的知识解决实际问题。
【教学方法】
教师通过设计方案,启发、引导、点拨学生,为学生创设一个自主、合作、探究的学习环境。同时,培养学生的合作意识,开发学生的发散思维能力。渗透认识事物、解决问题的方法,培养学生良好的思维品质。
【教学准备】
每组一个测量倾斜角的仪器(测角仪)、皮尺等测量工具。
【教学过程】
一、探究新知
(一)活动一内容:测量倾斜角
侧倾器的结构:度盘、铅锤和支杆组成。
1.把支架竖直插入地面,使支架的中心线、铅垂线和度盘的0°刻度线重合,这时度盘的顶线PQ在水平位置。
2.转动转盘,使度盘的直径对准目标M,记下此时铅垂线所指的度数。
(设计意图:根据测量数据,能求出目标的仰角或俯角,培养学生的使用工具的能力。)
(二)活动二内容:讨论测量底部可以到达的物体的高度的原理。
二、讨论测量底部不可以到达的物体的高度的原理
(一)当测量底部可以到达的物体的高度
1.在测点A安置测倾器,测得M的仰角∠MCE=α;
2.量出测点A到物体底部N的水平距离AN=l;
3.量出测倾器的高度AC=a,可求出MN的高度。
MN=ME+EN=l tanα+a
(二)当测量底部不可以直接到达的物体的高度
1.在测点A处安置测倾器,测得此时M的仰角∠MCE=α;
2.在测点A与物体之间B处安置测倾器,测得此时M的仰角∠MDE=β;
3.量出测倾器的高度AC=BD=a,以及测点A,B之间的距离AB=b。根据测量数据,可求出物体MN的高度。
(设计意图:掌握测量的原理 ,提醒学生注意方法的选择;不要忽略了测角仪到地面的高度。培养学生独立设计方案的能力。培养学生科学的思维方式和思维能力。)
三、实验模型
(一)实验1
课题 测量旗杆高
测量示意图
测量项目 AN的长 10.03m 9.97m 平均值:
测倾器的高 CD=1m CD=1m 平均值:
倾斜角 a=29°15′ a=30°45′ 平均值:
计算 旗杆MN的高度(精确到0.1m)
1.请根据测得的数据,填表中的空格;
2.通过计算得旗杆的高为(已知测倾器的高CD=1m)______米(精确到米)。
(二)在Rt△CME中,ME=CEtan30°=1.732,CE=1732
MN=ME+NE=17.32+1=18.32≈18
实验2
课题 在平面上测量地王大厦的高AB
测量示意图
测得数据 测量项目 ∠α ∠β CD的长
第一次 30°16’ 45°35’ 60.11M
第二次 30°44’ 45°25’ 59.89M
平均值
1.请根据测得的数据,填表中的空格;
2.通过计算得地王大厦的高为(已知测倾器的高CE=DF=1m)______米(精确到米)。
(三)在Rt△AEG中,EG=AG/tan30°=1.732AG
在Rt△AFG中,FG=AG/tan45°=AG
FG-EG=CD
1.732AG-AG=60
AG=60÷0.732≈81.96
AB=AG+1≈83(m)
(设计意图:培养学生动手操作,积极参与数学活动的能力,在活动中体现相互尊重和协调的能力,发展合作意识和科学精神。加深巩固解直角三角形的能力,解决实际问题。)
四、知识运用
例:如图,在某建筑物AC上,挂着“多彩云南”的宣传条幅BC,小明站在点F处,看条幅顶端B,测得仰角为,再往条幅方向前行20米到达点E处,看到条幅顶端B,测得仰角为,求宣传条幅BC的长(小明的身高不计,结果精确到0.1米)。
解:∵∠BFC =,∠BEC=,∠BCF=
∴∠EBF=∠EBC=
∴BE=EF=20
Rt△BCE
答:宣传条幅BC的长是17.3米。
(设计意图:通过典型例题培养学生独立设计方案和利用三角函数的方法的能力。培养学生科学的思维方式和思维能力。)
五、巩固训练
(一)如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度,标杆与旗杆的水平距离,人的眼睛与地面的高度,人与标杆的水平距离,求旗杆的高度。
(二)大楼AD的高为100米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60度,爬到楼顶D测得塔顶B点仰角为30度,求塔BC的高度。
(设计意图:总结数学活动经验,培养学生理论联系实际的能力。)
六、总结串联
本节课通过学习认识侧倾器、达到测量物体的高度的目标你有哪些收获与疑惑?
(设计意图:小结由学生发言,为他们提供一个互相交流的平台,让学生养成反思与总结的习惯,培养学生的语言概括能力。)
七、达标测试
(一)住宅区内的两幢楼,它们的高AB=CD=30m,两楼间的距离AC=24现了解甲楼对乙楼采光的影响情况。当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?
(二)甲乙两楼之间的距离为40米,小华从甲楼顶测乙楼顶仰角为=30 ,观测乙楼的底部俯角为=45 ,试用含、的三角函数式子表示乙楼的高=______________米。
0
30
30
60
60
90
90
P
Q
M
30°
0
30
30
60
60
90
90
P
Q
M
A
C
N
E
α
D
C
DDDD
C
E
F
A
G
B
α
β
1
