2024北京延庆高一(上)期末数学(PDF版无答案)
文档属性
| 名称 | 2024北京延庆高一(上)期末数学(PDF版无答案) |
|
|
| 格式 | |||
| 文件大小 | 923.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-18 00:00:00 | ||
图片预览



文档简介
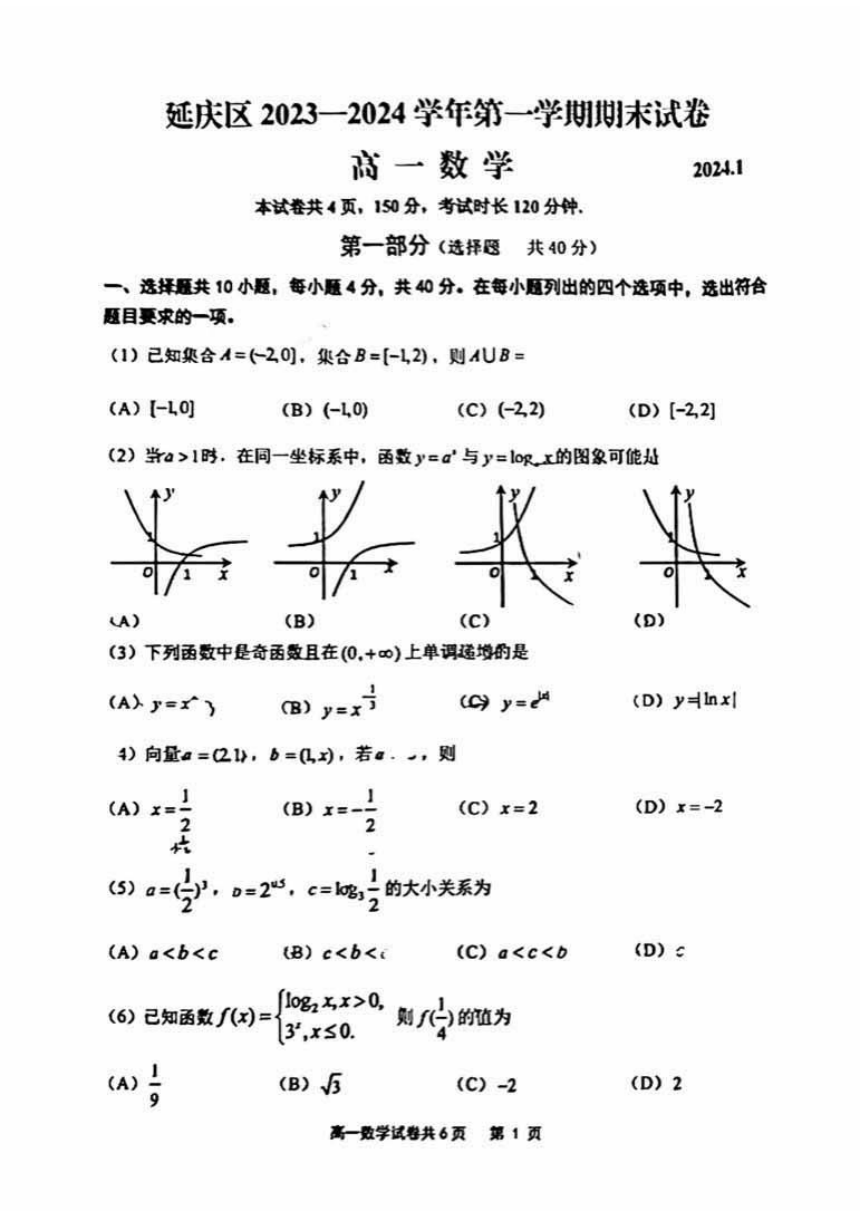
延庆区2023一2024学年第一学期末试卷
咸一数学
2024.1
本试卷共4页,150分,考试时长120分钟
第一部分(选择题
共40分)
一、进择题共10小题,每小题4分,共40分。在每小圆列出的四个选项中,选出符合
题目要求的一项。
(1)己知集合A=(20],集合B=[-L,2),则AUB=
(A)【-L0
(B)(-L0)
(c)(-22)
(D)[-2,2]
(2)当a>1时.在同一坐标系中,函数y=d与y=lo叹x的图象可能地
长
A】
(B)
(3)下列函数中是奇函数且在(0,+ )上单调递增的是
(A)y=)
)y=x
(9y=4
(D)yInxl
4)向量a=2,b=0),若a.,则
(A)x=
(8)x=-
(C)x=2
(D)x=-2
2
、
口=,2.c=3的大小关系为
(A)a(B)c(C)a(D)s
(6)已知函数f()=
55>0
3,x≤0.
则白的随为
(A)
(B)5
(C)-2
(D)2
高-数学试碧共6页第1页
)甲,乙两人在5天中每天加工多件的个数用茎叶图表示如下,中间一列竹划半花示
罗件个数的十位数,两边的数字戏示爱件个数的个位数,则下列结论正确的是
甲
98
1
732135
(.)在这5天中,甲加工翠件数的极更小于乙加工受件数的极差
(B)在这5天中,甲、乙两人加工罗件数的中位数相同
(C)在这5天中,甲日均加工号件数大于乙日均加工妥件数
(D)在这5天中,甲加工罗件数的方能小于乙加工妥件数的方差
(8)一个袋子中有大小和质地相间回的4个球其中有2个红色球(标号为1和2),2个绿
色球(标号为3和4),从纹中不放阿地依次随摸出2个球,每次执出一个球,设事
件S=“第一次摸到红球”,T=“第二次摸到红球”,R=两次都投到红球,G=“两
次都换到绿球”,M=两球颜色相同,N=两球顿色不同”,则下列说法错误的是
(A)M=N(B)R与G互斥但不对立(C)RUG=M(n)S与T相互独立
(9)已知等边△MBC的边长为6,D在AC上且AD=2DC,E为线段AB上的动点,求
女、|E+BD1的取值范围
(A)[2N5,4
(B)2W5,2)
(c)[4,2j
(D)[4,可
(10)假设有机体生存时碳14的含量为m。,那么有机体死亡x年后体内碳14的含征y满
足的关系为y=ma(其中m。,a都是非实数),若测得死亡5730年后的古生
物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品,体内碳
14的含量为025.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡
时间为(取g2≈03,1g3=05)
(A)10550年
(B)7550年
(C)8550年
(D)9550年
高一数学试卷共6页第2页
咸一数学
2024.1
本试卷共4页,150分,考试时长120分钟
第一部分(选择题
共40分)
一、进择题共10小题,每小题4分,共40分。在每小圆列出的四个选项中,选出符合
题目要求的一项。
(1)己知集合A=(20],集合B=[-L,2),则AUB=
(A)【-L0
(B)(-L0)
(c)(-22)
(D)[-2,2]
(2)当a>1时.在同一坐标系中,函数y=d与y=lo叹x的图象可能地
长
A】
(B)
(3)下列函数中是奇函数且在(0,+ )上单调递增的是
(A)y=)
)y=x
(9y=4
(D)yInxl
4)向量a=2,b=0),若a.,则
(A)x=
(8)x=-
(C)x=2
(D)x=-2
2
、
口=,2.c=3的大小关系为
(A)a
(6)已知函数f()=
55>0
3,x≤0.
则白的随为
(A)
(B)5
(C)-2
(D)2
高-数学试碧共6页第1页
)甲,乙两人在5天中每天加工多件的个数用茎叶图表示如下,中间一列竹划半花示
罗件个数的十位数,两边的数字戏示爱件个数的个位数,则下列结论正确的是
甲
98
1
732135
(.)在这5天中,甲加工翠件数的极更小于乙加工受件数的极差
(B)在这5天中,甲、乙两人加工罗件数的中位数相同
(C)在这5天中,甲日均加工号件数大于乙日均加工妥件数
(D)在这5天中,甲加工罗件数的方能小于乙加工妥件数的方差
(8)一个袋子中有大小和质地相间回的4个球其中有2个红色球(标号为1和2),2个绿
色球(标号为3和4),从纹中不放阿地依次随摸出2个球,每次执出一个球,设事
件S=“第一次摸到红球”,T=“第二次摸到红球”,R=两次都投到红球,G=“两
次都换到绿球”,M=两球颜色相同,N=两球顿色不同”,则下列说法错误的是
(A)M=N(B)R与G互斥但不对立(C)RUG=M(n)S与T相互独立
(9)已知等边△MBC的边长为6,D在AC上且AD=2DC,E为线段AB上的动点,求
女、|E+BD1的取值范围
(A)[2N5,4
(B)2W5,2)
(c)[4,2j
(D)[4,可
(10)假设有机体生存时碳14的含量为m。,那么有机体死亡x年后体内碳14的含征y满
足的关系为y=ma(其中m。,a都是非实数),若测得死亡5730年后的古生
物样品,体内碳14的含量为0.5,又测得死亡11460年后这类古生物样品,体内碳
14的含量为025.如果测得某古生物样品碳14的含量为0.3,推测此古生物的死亡
时间为(取g2≈03,1g3=05)
(A)10550年
(B)7550年
(C)8550年
(D)9550年
高一数学试卷共6页第2页
同课章节目录
