多边形的内角和
图片预览


文档简介
课件11张PPT。§7.3.2 多边形的内角和(第1课时) 人教版义务教育课程标准实验教科书 七年级(下册)2、若任意给出一个多边形,如二十边形,要求它的内角和,
如果采用上述的度量法,就得量出二十个内角的度数,再计算。
这样很麻烦。所以请同学们思考这样一个问题:
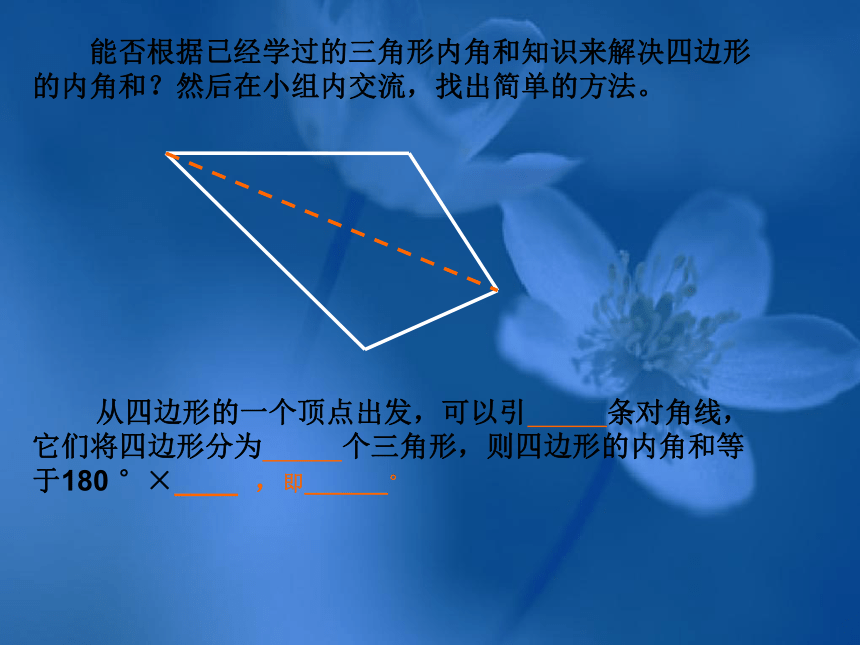
从四边形的一个顶点出发,可以引 条对角线,
它们将四边形分为 个三角形,则四边形的内角和等
于180 °×____ ,即_______° 能否根据已经学过的三角形内角和知识来解决四边形
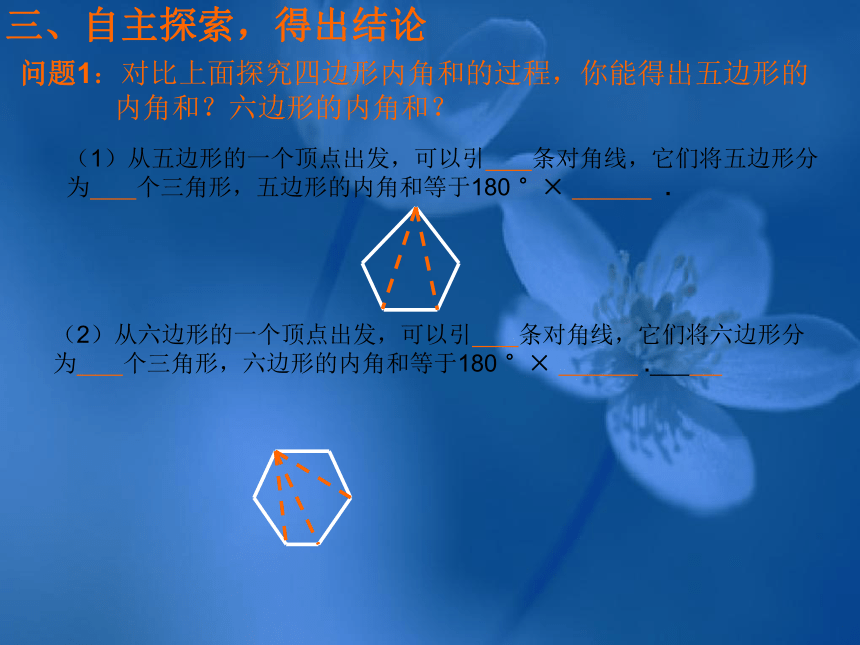
的内角和?然后在小组内交流,找出简单的方法。三、自主探索,得出结论 问题1:对比上面探究四边形内角和的过程,你能得出五边形的
内角和?六边形的内角和?(1)从五边形的一个顶点出发,可以引 条对角线,它们将五边形分
为 个三角形,五边形的内角和等于180 °× .(2)从六边形的一个顶点出发,可以引 条对角线,它们将六边形分
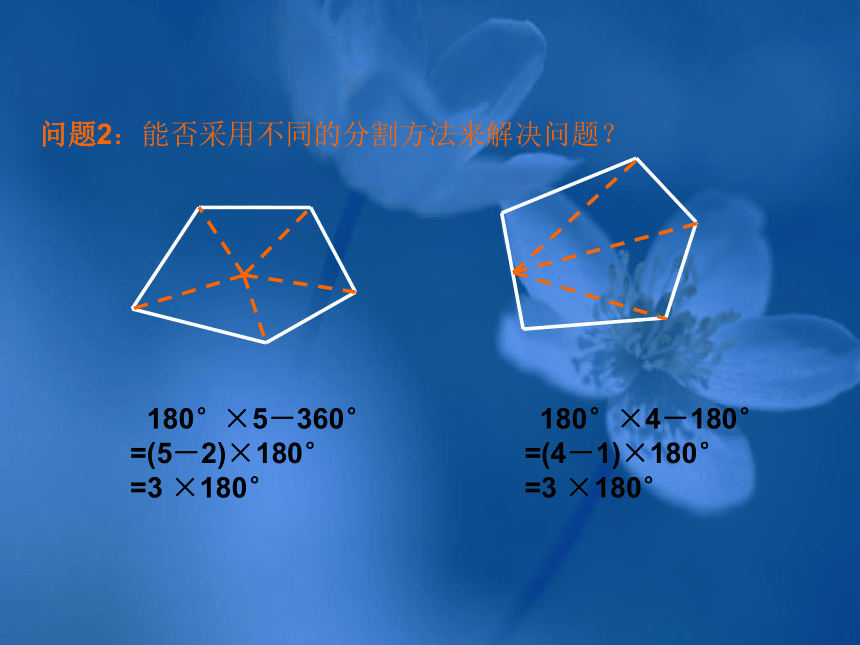
为 个三角形,六边形的内角和等于180 °× . 问题2:能否采用不同的分割方法来解决问题? 180°×5-360°
=(5-2)×180°
=3 ×180° 180°×4-180°
=(4-1)×180°
=3 ×180°问题3:n边形的内角和是多少? 从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180°× . 180°n-360°=(n-2)×180°四、应用新知,尝试练习例2、解答题
已知一个多边形的内角和为900°,则它是几边形?
若一个多边形是二十边形,则它的内角和为 .例1、填空
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
例3、教科书82页例1:练一练1、如图:
(1)作多边形所有过顶点A的对角线,并分别用字母表达出来。
(2)求这个多边形的内角和。F解: (1)过顶点A的对角线共有 三 条,分别是AC、AD和AE . (2)这个多边形的内角和是:(6-2) · 180 = 720(度).五、归纳总结,形成体系 1、归纳本节课学习了以下主要内容:
(1)探索了n边形的内角和公式
(2)学会转化思想 ( 2)、小明想:2008年奥运会在北京召开,设计一个内角和为 2008度的多边形
图案多有意义,小明的想法能实现吗?
2.作业布置
(1)、如果一个多边形的内角和是1440度,那么这是_____________边形。
如果采用上述的度量法,就得量出二十个内角的度数,再计算。
这样很麻烦。所以请同学们思考这样一个问题:
从四边形的一个顶点出发,可以引 条对角线,
它们将四边形分为 个三角形,则四边形的内角和等
于180 °×____ ,即_______° 能否根据已经学过的三角形内角和知识来解决四边形
的内角和?然后在小组内交流,找出简单的方法。三、自主探索,得出结论 问题1:对比上面探究四边形内角和的过程,你能得出五边形的
内角和?六边形的内角和?(1)从五边形的一个顶点出发,可以引 条对角线,它们将五边形分
为 个三角形,五边形的内角和等于180 °× .(2)从六边形的一个顶点出发,可以引 条对角线,它们将六边形分
为 个三角形,六边形的内角和等于180 °× . 问题2:能否采用不同的分割方法来解决问题? 180°×5-360°
=(5-2)×180°
=3 ×180° 180°×4-180°
=(4-1)×180°
=3 ×180°问题3:n边形的内角和是多少? 从n边形的一个顶点出发,可以引 条对角线,它们将n边形分为 个三角形,n边形的内角和等于180°× . 180°n-360°=(n-2)×180°四、应用新知,尝试练习例2、解答题
已知一个多边形的内角和为900°,则它是几边形?
若一个多边形是二十边形,则它的内角和为 .例1、填空
如果一个四边形的一组对角互补,那么另一组对角有什么关系?
例3、教科书82页例1:练一练1、如图:
(1)作多边形所有过顶点A的对角线,并分别用字母表达出来。
(2)求这个多边形的内角和。F解: (1)过顶点A的对角线共有 三 条,分别是AC、AD和AE . (2)这个多边形的内角和是:(6-2) · 180 = 720(度).五、归纳总结,形成体系 1、归纳本节课学习了以下主要内容:
(1)探索了n边形的内角和公式
(2)学会转化思想 ( 2)、小明想:2008年奥运会在北京召开,设计一个内角和为 2008度的多边形
图案多有意义,小明的想法能实现吗?
2.作业布置
(1)、如果一个多边形的内角和是1440度,那么这是_____________边形。
