直线和圆的位置关系复习课(江西省宜春地区)
文档属性
| 名称 | 直线和圆的位置关系复习课(江西省宜春地区) |  | |
| 格式 | rar | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-01-11 13:19:00 | ||
图片预览





文档简介
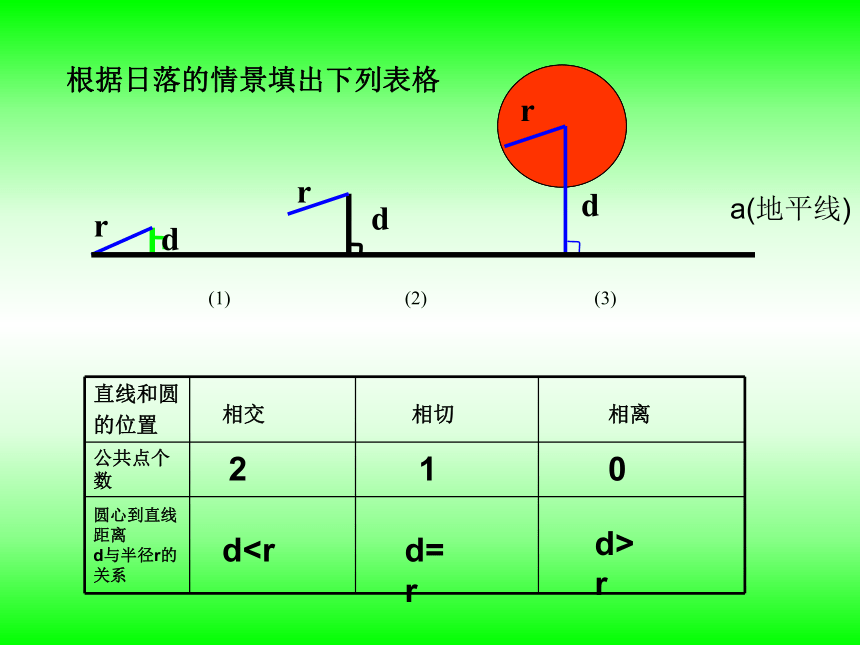
课件19张PPT。直线和圆的位置关系复习课一、知识结构直线和圆的位置关系切线的判定和性质切线长定理直线和圆的三种位置关系:相离、相切、相交〈一〉、直线和圆的位置关系二﹑旧知回顾、“大漠孤烟直,长河落日圆” 是唐朝诗人王维的诗句,它描述了黄昏日落时分塞外特有的景象。请观察图中日落的情景, 根据直线与圆的公共点的个数回顾一下,直线和圆的位置关系有几种?a(地平线)
(1)(3)(2)ddd rrrdr210根据日落的情景填出下列表格相离
相切
相交小结我们可以从两个方面去判断直线和圆的位置关系
(1)根据直线和圆的公共点的个数
(2)根据圆心到直线的距离和半径之间的数量关系2、已知⊙O的直径是11cm,点O到直线a的
距离是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.
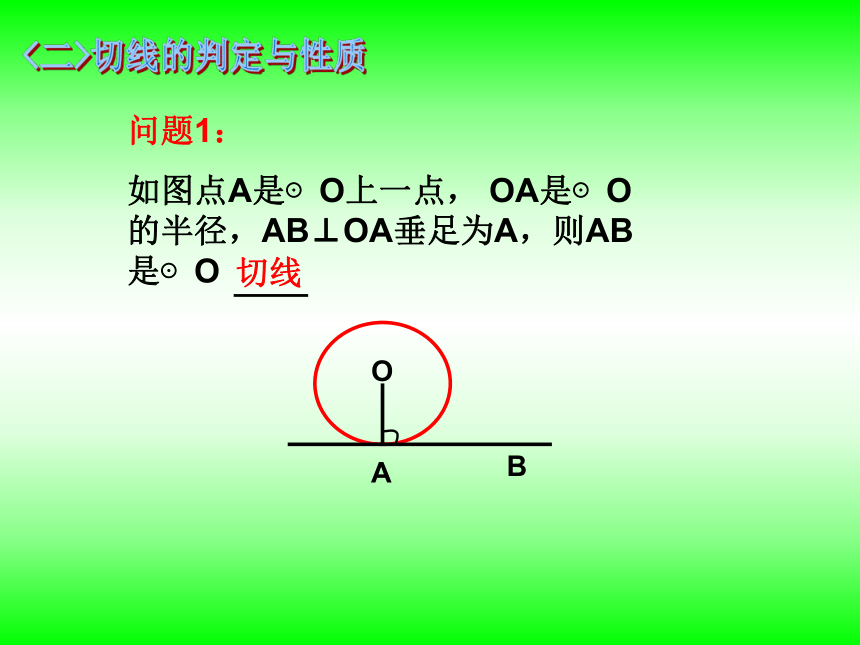
考题再现填空:1、(2007福建)如图,把太阳看成一个圆,则太阳与地平线a的位置关系是 (填相交、相切、相离)动动脑筋相切一个相离(1)3、已知:圆的半径等于10厘米,直线a和圆有唯一的公共点,则圆心到直线a的距离是 厘米10a<二>切线的判定与性质问题1:
如图点A是⊙O上一点, OA是⊙O的半径,AB⊥OA垂足为A,则AB是⊙O切线AOB切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端是已知给出时,只需证明该直线垂直于半径。如图:判断下列图形中的直 线a是否是圆的切线问题2:如图AB是⊙O的切线,点A是⊙O上的一点则 AB ___ OA
ABO切线的性质:
圆的切线垂直于经过切点的半径.
⊥如图,P是⊙O外一点,PA,PB是⊙O的两条切线, 线段PA,PB叫做点P到⊙O的OPAB切线长。
连接OP,则∠APO___ ∠ BPOPA PB==<三>切线长定理 切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。如图:(1)AB、AC、BC是⊙O的切线,切点分别是D、E、F,请找出图中相等的线段ABCDEFAD=AE
BD=BF
CE=CF (2)移动AC到如图所示的位置,请找出图中相等的线段。并观察△ABC的周长与切线长BD、BF的关系ACEAD=AE BD=BF CE=CF△ABC的周长=2BD1、(2007浙江)如图:PA切⊙O于点A,
该圆的半径为3,PO=5,则PA的长等于4A0P 2、(2007孝感)如图:A B是⊙O上的两点,
AC是⊙O的切线,∠B=700,则
∠BAC=
O AB200填空:C 3、已知:如图,PA、PB是⊙O的切线,
切点分别是A、B,Q为⊙O上一点,过
Q点作⊙O的切线,交PA、PB于E、F点,
已知PA=12CM, 则△PEF的周长
——(2)(1)PABQEFO24(3)例.(2007年泸州)已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.∵OD=OB,OC=OC,
∴△ODC≌△OBC.
∴∠ODC=∠OBC.CBADO1234证明:连结OD.
∵BC是⊙O的切线,
∴∠OBC=90°.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3, ∠2=∠4
∴∠3=∠4.
∴∠ODC=90°.
∴DC是⊙O的切线.
规律总结:证明一条直线是圆的切线,常常要添加辅助线,如果直线与圆有一个公共点,则连接这点和圆心,证明直线垂直于经过这点的半径.(2007年十堰)PA是圆O的切线,切点是A,过点A作AH⊥OP于点H交⊙O于B。求证:PB是⊙O的切线
BAOPH又∵ AH⊥OP于点H
∴BM=AM
∴ ∠BOP=∠AOP(在同圆和等圆 中相等的弧所对的圆心角相等)
在△BOP和△AOP中
∵ BO=AO
∠BOP=∠AOP
PO=PO
∴ △BOP≌△AOP(SAS)
∴ ∠OBP=∠OAP=900
∴PB是⊙O的切线
解:连结OB、OA
∵ PA是圆O的切线,切点是A ∴∠OAP=900
⌒⌒M考题再现课堂小结1 今天我们一起复习哪些圆的有关知识?
作业:已知 Rt△ABC的斜边AB=6cm,直角边AC=3cm,以点C为圆心,半径分别为2cm和4cm画两个圆,这两个圆与AB有怎样的位置关系?当半径为多长时,AB与圆C相切?如图所示,AB为⊙O的直径,C是⊙O上的一点,D在AB的 延长线上,∠DCB= ∠A。
求证:CD是⊙O的切线DBCAOABCD证明:∵ AB为⊙O的直径
∴ ∠ACB=900 ∵ OA=OC
∴ ∠A= ∠ACO又∵ ∠ACO + ∠ OCB= 900∠DCB= ∠A∴ ∠ DCB + ∠ OCB = 900即∠ OCB=900
∴ CD是⊙O的切线中考摸拟
(1)(3)(2)ddd rrrd
相切
相交小结我们可以从两个方面去判断直线和圆的位置关系
(1)根据直线和圆的公共点的个数
(2)根据圆心到直线的距离和半径之间的数量关系2、已知⊙O的直径是11cm,点O到直线a的
距离是5.5cm,则⊙O与直线a的位置关系是 ___ _;
直线a与⊙O的公共点个数是____.
考题再现填空:1、(2007福建)如图,把太阳看成一个圆,则太阳与地平线a的位置关系是 (填相交、相切、相离)动动脑筋相切一个相离(1)3、已知:圆的半径等于10厘米,直线a和圆有唯一的公共点,则圆心到直线a的距离是 厘米10a<二>切线的判定与性质问题1:
如图点A是⊙O上一点, OA是⊙O的半径,AB⊥OA垂足为A,则AB是⊙O切线AOB切线的判定定理:经过半径外端
并且垂直于这条半径的直线是圆
的切线。一般情况下,要证明一条直线为圆的切线,它过半径外端是已知给出时,只需证明该直线垂直于半径。如图:判断下列图形中的直 线a是否是圆的切线问题2:如图AB是⊙O的切线,点A是⊙O上的一点则 AB ___ OA
ABO切线的性质:
圆的切线垂直于经过切点的半径.
⊥如图,P是⊙O外一点,PA,PB是⊙O的两条切线, 线段PA,PB叫做点P到⊙O的OPAB切线长。
连接OP,则∠APO___ ∠ BPOPA PB==<三>切线长定理 切线长定理:
从圆外一点引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角。如图:(1)AB、AC、BC是⊙O的切线,切点分别是D、E、F,请找出图中相等的线段ABCDEFAD=AE
BD=BF
CE=CF (2)移动AC到如图所示的位置,请找出图中相等的线段。并观察△ABC的周长与切线长BD、BF的关系ACEAD=AE BD=BF CE=CF△ABC的周长=2BD1、(2007浙江)如图:PA切⊙O于点A,
该圆的半径为3,PO=5,则PA的长等于4A0P 2、(2007孝感)如图:A B是⊙O上的两点,
AC是⊙O的切线,∠B=700,则
∠BAC=
O AB200填空:C 3、已知:如图,PA、PB是⊙O的切线,
切点分别是A、B,Q为⊙O上一点,过
Q点作⊙O的切线,交PA、PB于E、F点,
已知PA=12CM, 则△PEF的周长
——(2)(1)PABQEFO24(3)例.(2007年泸州)已知AB是⊙O的直径,BC是⊙O的切线,切点为B,OC平行于弦AD.求证:DC是⊙O的切线.∵OD=OB,OC=OC,
∴△ODC≌△OBC.
∴∠ODC=∠OBC.CBADO1234证明:连结OD.
∵BC是⊙O的切线,
∴∠OBC=90°.
∵OA=OD,∴∠1=∠2,
∵AD∥OC,∴∠1=∠3, ∠2=∠4
∴∠3=∠4.
∴∠ODC=90°.
∴DC是⊙O的切线.
规律总结:证明一条直线是圆的切线,常常要添加辅助线,如果直线与圆有一个公共点,则连接这点和圆心,证明直线垂直于经过这点的半径.(2007年十堰)PA是圆O的切线,切点是A,过点A作AH⊥OP于点H交⊙O于B。求证:PB是⊙O的切线
BAOPH又∵ AH⊥OP于点H
∴BM=AM
∴ ∠BOP=∠AOP(在同圆和等圆 中相等的弧所对的圆心角相等)
在△BOP和△AOP中
∵ BO=AO
∠BOP=∠AOP
PO=PO
∴ △BOP≌△AOP(SAS)
∴ ∠OBP=∠OAP=900
∴PB是⊙O的切线
解:连结OB、OA
∵ PA是圆O的切线,切点是A ∴∠OAP=900
⌒⌒M考题再现课堂小结1 今天我们一起复习哪些圆的有关知识?
作业:已知 Rt△ABC的斜边AB=6cm,直角边AC=3cm,以点C为圆心,半径分别为2cm和4cm画两个圆,这两个圆与AB有怎样的位置关系?当半径为多长时,AB与圆C相切?如图所示,AB为⊙O的直径,C是⊙O上的一点,D在AB的 延长线上,∠DCB= ∠A。
求证:CD是⊙O的切线DBCAOABCD证明:∵ AB为⊙O的直径
∴ ∠ACB=900 ∵ OA=OC
∴ ∠A= ∠ACO又∵ ∠ACO + ∠ OCB= 900∠DCB= ∠A∴ ∠ DCB + ∠ OCB = 900即∠ OCB=900
∴ CD是⊙O的切线中考摸拟
同课章节目录
