第7章锐角三角函数 期末综合复习训练题 2022—2023学年苏科版九年级数学下册(含解析)
文档属性
| 名称 | 第7章锐角三角函数 期末综合复习训练题 2022—2023学年苏科版九年级数学下册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 773.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 22:46:23 | ||
图片预览



文档简介
2022-2023学年苏科版九年级数学下册《第7章锐角三角函数》
期末综合复习训练题(附答案)
一、单选题
1.已知在中,,,,那么的长为( )
A. B. C. D.
2.已知,则下列各式中正确的是( )
A. B. C. D.
3.在中,,,,则的长为( )
A.6 B.7 C.8 D.9
4.在中,已知,那么下列结论正确的是( )
A. B. C. D.
5.如图,是一条斜坡,若,点到点的铅垂距离为,则斜坡的坡度为( )
A. B. C. D.
6.已知是半径为6的圆的一条弦,若,则所对圆周角的度数是( )
A. B.或 C.或 D.
7.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上).为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升到达A处,在A处观察B地的俯角为,则B,C两地之间的距离为( )
A. B. C. D.
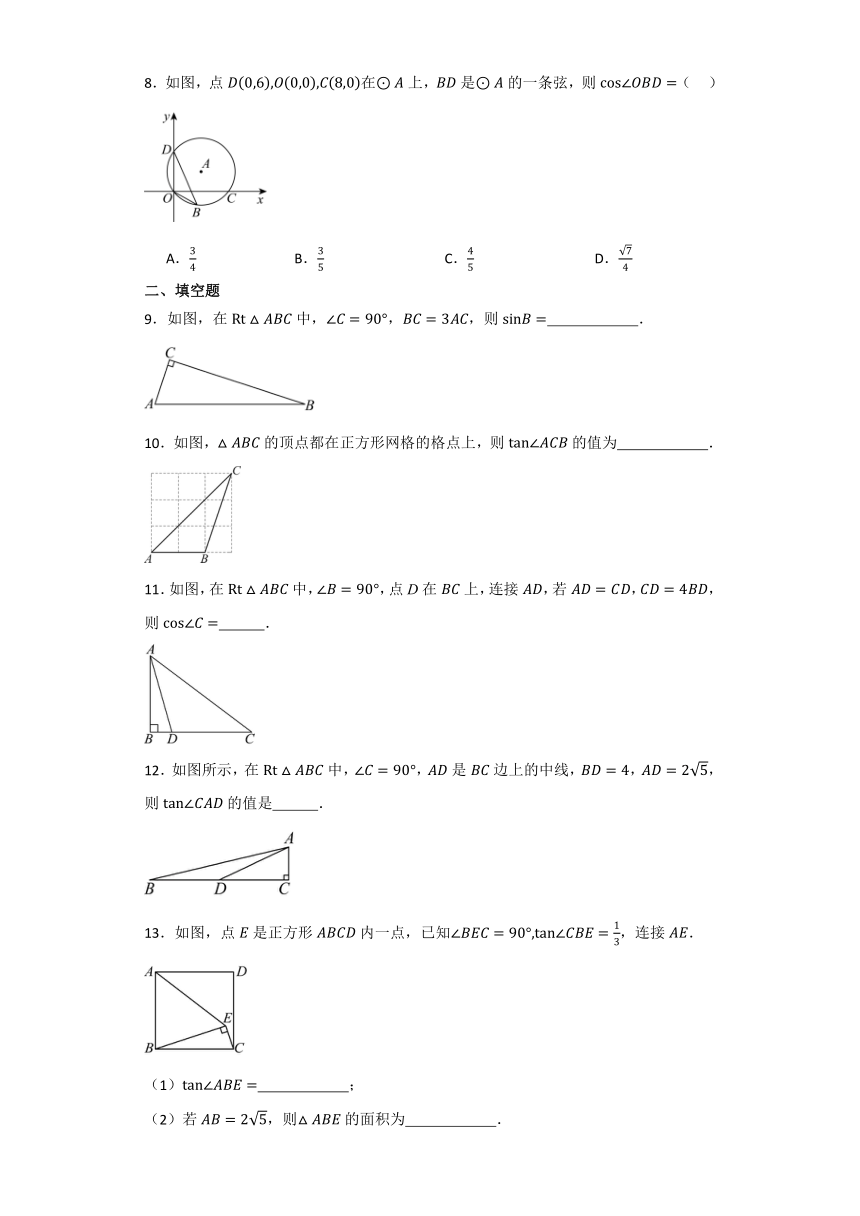
8.如图,点在上,是的一条弦,则( )
A. B. C. D.
二、填空题
9.如图,在中,,,则 .
10.如图,的顶点都在正方形网格的格点上,则的值为 .
11.如图,在中,,点D在上,连接,若,,则 .
12.如图所示,在中,,是边上的中线,,,则的值是 .
13.如图,点是正方形内一点,已知,连接.
(1) ;
(2)若,则的面积为 .
14.如图,一段东西向的限速公路长米,在此公路的南面有一监测点,从监测点观察,限速公路的端点在监测点的北偏西方向,端点在监测点的东北方向,那么监测点到限速公路的距离是 米(结果保留根号).
15.如图,某兴趣小组测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).则旗杆EF的高度为 .(结果保留整数参考数据:,)
16.如图,点C在线段上,且,分别以为边在线段的同侧作正方形,连接,则 .
三、解答题
17.计算:
18.在中,,,,解这个直角三角形.
19.随着技术进步和成果转化,在我国无人机的用武之地越来越多,农林植保、应急救援、文物保护、电力巡检……,加速赋能千行百业.如图,某农业示范基地用无人机对一块试验田进行监测作业时,无人机在点A处,无人机距地面高度为120米,此时测得试验田一侧边界点C处俯角为,无人机垂直下降40米至点B处,又测得试验田另一侧边界点D处俯角为,且点C,O,D在同一条直线上,求点C与点D的距离.(参考数据:,结果保留整数)
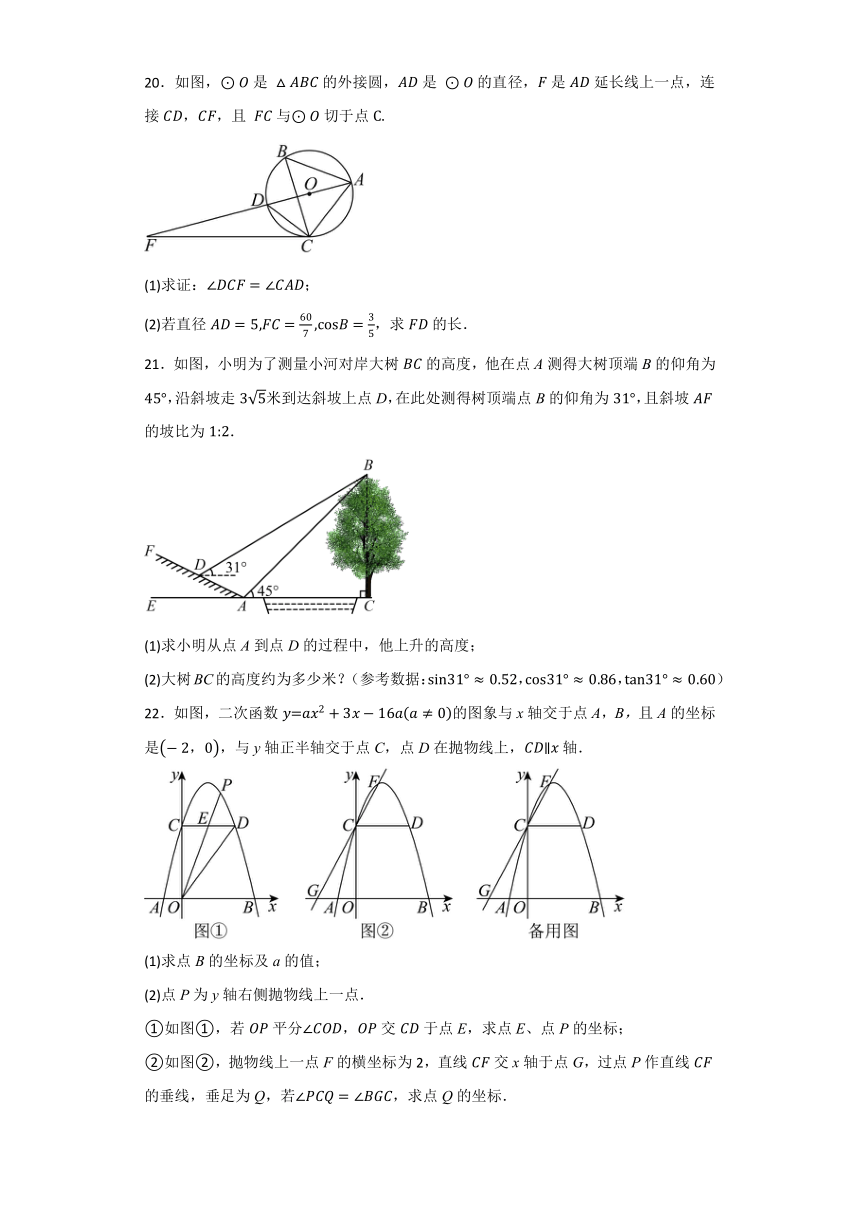
20.如图,是 的外接圆,是 的直径,是延长线上一点,连接,,且 与切于点
(1)求证:;
(2)若直径,求的长.
21.如图,小明为了测量小河对岸大树的高度,他在点A测得大树顶端B的仰角为,沿斜坡走米到达斜坡上点D,在此处测得树顶端点B的仰角为,且斜坡的坡比为.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:,,)
22.如图,二次函数的图象与x轴交于点A,B,且A的坐标是,与y轴正半轴交于点C,点D在抛物线上,轴.
(1)求点B的坐标及a的值;
(2)点P为y轴右侧抛物线上一点.
①如图①,若平分,交于点E,求点E、点P的坐标;
②如图②,抛物线上一点F的横坐标为2,直线交x轴于点G,过点P作直线的垂线,垂足为Q,若,求点Q的坐标.
参考答案
1.解:∵,,,
∴,即,
∴,
故选:D.
2.解:A.由于一个锐角的余弦值随着锐角的增大而减小,而,所以 ,因此选项A不符合题意;
B.由于一个锐角的正切值随着锐角的增大而增大,而所以,即,因此选项B不符合题意;
C.由于,而,即,所以,即,因此选项C不符合题意;
D.由于锐角的对边除以斜边,锐角的对边除以锐角的邻边,而锐角的邻边小于斜边,所以,因此选项D符合题意.
故选:D.
3.解:∵,,,
∴,
解得:,
故选:C
4.解:∵,
∴,
∴是直角三角形,且,如图,
∴,,,,
∴A、C、D错误,故不符合要求;B正确,故符合要求;
故选:B.
5.解:根据题意得:
,,
,
斜坡的坡度为:,
故选:.
6.解:如图,于C,则,
在中, ,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵四边形是圆内接四边形,
∴,
故所对圆周角的度数是或,
故选:C.
7.解:由题意得,,
∴在中,
∴B,C两地之间的距离为.
故选A.
8.解:连接,则:,
∵,
∴,
∴,
∴;
故选C.
9.解:∵,,
∴设,则:,
∴,
∴.
故答案为:.
10.解:作于点,由图形可得,
,,,
∴,
解得:,,
∴,
故答案为:;
11.解:设,则,
∴,,
∴
∴,
故答案为:.
12.解:∵是边上的中线,
∴,
在中,,,
∴,
∴,
故答案为:2.
13.解:(1)在中,,由,设,
.
∵四边形是正方形,
∴,
又,
.
.
故答案为:3
(2)如图,过点作于点.
,
.
.
在中,由,可设,
由勾股定理,得.
四边形是正方形,
.
,即,解得(负值舍去),则.
.
故答案为:9
14.解:如图,过点作于点,
则,
设米,
由题意得:
,,
是等腰直角三角形,
米,
在中,
,
,
又,
(米),
,
,
解得:,
即监测点到限速公路的距离是米,
故答案为:.
15.解:过点A作于点M,过点C作于点N.设米,
在中,
∵,
∴
∴,
∵,
∴
在中,
∵
∴,即,
∴,
∴,
解得:,
即(米);
∴(米).
所以,旗杆的高度约为9.8米.
故答案为:米
16.解:如图,连接,
由正方形的性质可知,,
∴,
设,则,
由勾股定理得,,
∴,
故答案为:.
17.解:
18.解:由题意知: ,
解得:,
,
,
由,
解得:,
,
.
19.解:由题意,得:,,
在中:,
∴,
在中,,
∴,
∴;
答:点C与点D的距离约为.
20.(1)证明:连接,
是的切线,
,
,
是的直径,
,
,
,
,
;
(2)解:由圆周角定理得:,
,
,
,
由勾股定理得:,
,,
,
,
设,则,
在中,,即,
解得:(舍去),,
.
21.(1)解:作于H,如图1所示:
AI
在中,
∵,
∴,
∵,
∴,
∴.
答:小明从点A到点D的过程中,他上升的高度为3米;
(2)解:如图2所示:延长交于点G,
设,
由题意得,,
∴,
∵,
∴,
在中,,
∴,
在中,,
∴.
∵,
∴,
解得:.
答:大树的高度约为米.
22.(1)解:将点代入,
则解得,
∴,
令,则,解得或,
则;
(2)①过点E作于G,如图,
令得,则点,
∵轴,
∴点D的纵坐标为8,
∴,解得,或,
则点,
∵平分,,,
∴,
设,则,
∵,
∴,解得,
则点,
设直线的解析式为,
将代入,解得,
则直线的解析式为,
联立方程组,解得或(舍去),
则点.
②当时,,
则点,
设直线的函数解析式为,
把点、点代入,得,解得,
则直线的函数解析式为,
∴点,
那么,
∵,
∴,
∴,
(Ⅰ)若点在点上方,
过点作轴的平行线,交轴于点,如图,
∵,
∴轴,
∵轴,
∴点P与点Q重合,,
∴,
∴,
∴设,则,
∵轴,
∴,
∴,
则,
∵,
∴,
∴,
∴或(舍去),
∴.
把代入,得,
∴;
(Ⅱ)若点在点下方,
过点作轴,交的延长线于点,过点作的垂线,垂足为,交轴于点.如图,
∴,
∴四边形是矩形,
∴,
∵轴,
∴,,
∴ ,
∴设,则,
∵,,
∴,
又∵,
∴,
∴,
∴,,
则,,
那么,
代入,得,
∴(舍去),,
∴,
代入得,
∴.
综上所述,或.
期末综合复习训练题(附答案)
一、单选题
1.已知在中,,,,那么的长为( )
A. B. C. D.
2.已知,则下列各式中正确的是( )
A. B. C. D.
3.在中,,,,则的长为( )
A.6 B.7 C.8 D.9
4.在中,已知,那么下列结论正确的是( )
A. B. C. D.
5.如图,是一条斜坡,若,点到点的铅垂距离为,则斜坡的坡度为( )
A. B. C. D.
6.已知是半径为6的圆的一条弦,若,则所对圆周角的度数是( )
A. B.或 C.或 D.
7.如图,某地修建高速公路,要从B地向C地修一条隧道(B,C在同一水平面上).为了测量B,C两地之间的距离,某工程师乘坐热气球从C地出发,垂直上升到达A处,在A处观察B地的俯角为,则B,C两地之间的距离为( )
A. B. C. D.
8.如图,点在上,是的一条弦,则( )
A. B. C. D.
二、填空题
9.如图,在中,,,则 .
10.如图,的顶点都在正方形网格的格点上,则的值为 .
11.如图,在中,,点D在上,连接,若,,则 .
12.如图所示,在中,,是边上的中线,,,则的值是 .
13.如图,点是正方形内一点,已知,连接.
(1) ;
(2)若,则的面积为 .
14.如图,一段东西向的限速公路长米,在此公路的南面有一监测点,从监测点观察,限速公路的端点在监测点的北偏西方向,端点在监测点的东北方向,那么监测点到限速公路的距离是 米(结果保留根号).
15.如图,某兴趣小组测量学校旗杆的高度.已知小亮站着测量,眼睛与地面的距离是1.7米,看旗杆顶部E的仰角为30°;小敏蹲着测量,眼睛与地面的距离是0.7米,看旗杆顶部E的仰角为45°.两人相距5米且位于旗杆同侧(点B、D、F在同一直线上).则旗杆EF的高度为 .(结果保留整数参考数据:,)
16.如图,点C在线段上,且,分别以为边在线段的同侧作正方形,连接,则 .
三、解答题
17.计算:
18.在中,,,,解这个直角三角形.
19.随着技术进步和成果转化,在我国无人机的用武之地越来越多,农林植保、应急救援、文物保护、电力巡检……,加速赋能千行百业.如图,某农业示范基地用无人机对一块试验田进行监测作业时,无人机在点A处,无人机距地面高度为120米,此时测得试验田一侧边界点C处俯角为,无人机垂直下降40米至点B处,又测得试验田另一侧边界点D处俯角为,且点C,O,D在同一条直线上,求点C与点D的距离.(参考数据:,结果保留整数)
20.如图,是 的外接圆,是 的直径,是延长线上一点,连接,,且 与切于点
(1)求证:;
(2)若直径,求的长.
21.如图,小明为了测量小河对岸大树的高度,他在点A测得大树顶端B的仰角为,沿斜坡走米到达斜坡上点D,在此处测得树顶端点B的仰角为,且斜坡的坡比为.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:,,)
22.如图,二次函数的图象与x轴交于点A,B,且A的坐标是,与y轴正半轴交于点C,点D在抛物线上,轴.
(1)求点B的坐标及a的值;
(2)点P为y轴右侧抛物线上一点.
①如图①,若平分,交于点E,求点E、点P的坐标;
②如图②,抛物线上一点F的横坐标为2,直线交x轴于点G,过点P作直线的垂线,垂足为Q,若,求点Q的坐标.
参考答案
1.解:∵,,,
∴,即,
∴,
故选:D.
2.解:A.由于一个锐角的余弦值随着锐角的增大而减小,而,所以 ,因此选项A不符合题意;
B.由于一个锐角的正切值随着锐角的增大而增大,而所以,即,因此选项B不符合题意;
C.由于,而,即,所以,即,因此选项C不符合题意;
D.由于锐角的对边除以斜边,锐角的对边除以锐角的邻边,而锐角的邻边小于斜边,所以,因此选项D符合题意.
故选:D.
3.解:∵,,,
∴,
解得:,
故选:C
4.解:∵,
∴,
∴是直角三角形,且,如图,
∴,,,,
∴A、C、D错误,故不符合要求;B正确,故符合要求;
故选:B.
5.解:根据题意得:
,,
,
斜坡的坡度为:,
故选:.
6.解:如图,于C,则,
在中, ,,
∴,
∴,
∵,,
∴,
∴,
∴,
∵四边形是圆内接四边形,
∴,
故所对圆周角的度数是或,
故选:C.
7.解:由题意得,,
∴在中,
∴B,C两地之间的距离为.
故选A.
8.解:连接,则:,
∵,
∴,
∴,
∴;
故选C.
9.解:∵,,
∴设,则:,
∴,
∴.
故答案为:.
10.解:作于点,由图形可得,
,,,
∴,
解得:,,
∴,
故答案为:;
11.解:设,则,
∴,,
∴
∴,
故答案为:.
12.解:∵是边上的中线,
∴,
在中,,,
∴,
∴,
故答案为:2.
13.解:(1)在中,,由,设,
.
∵四边形是正方形,
∴,
又,
.
.
故答案为:3
(2)如图,过点作于点.
,
.
.
在中,由,可设,
由勾股定理,得.
四边形是正方形,
.
,即,解得(负值舍去),则.
.
故答案为:9
14.解:如图,过点作于点,
则,
设米,
由题意得:
,,
是等腰直角三角形,
米,
在中,
,
,
又,
(米),
,
,
解得:,
即监测点到限速公路的距离是米,
故答案为:.
15.解:过点A作于点M,过点C作于点N.设米,
在中,
∵,
∴
∴,
∵,
∴
在中,
∵
∴,即,
∴,
∴,
解得:,
即(米);
∴(米).
所以,旗杆的高度约为9.8米.
故答案为:米
16.解:如图,连接,
由正方形的性质可知,,
∴,
设,则,
由勾股定理得,,
∴,
故答案为:.
17.解:
18.解:由题意知: ,
解得:,
,
,
由,
解得:,
,
.
19.解:由题意,得:,,
在中:,
∴,
在中,,
∴,
∴;
答:点C与点D的距离约为.
20.(1)证明:连接,
是的切线,
,
,
是的直径,
,
,
,
,
;
(2)解:由圆周角定理得:,
,
,
,
由勾股定理得:,
,,
,
,
设,则,
在中,,即,
解得:(舍去),,
.
21.(1)解:作于H,如图1所示:
AI
在中,
∵,
∴,
∵,
∴,
∴.
答:小明从点A到点D的过程中,他上升的高度为3米;
(2)解:如图2所示:延长交于点G,
设,
由题意得,,
∴,
∵,
∴,
在中,,
∴,
在中,,
∴.
∵,
∴,
解得:.
答:大树的高度约为米.
22.(1)解:将点代入,
则解得,
∴,
令,则,解得或,
则;
(2)①过点E作于G,如图,
令得,则点,
∵轴,
∴点D的纵坐标为8,
∴,解得,或,
则点,
∵平分,,,
∴,
设,则,
∵,
∴,解得,
则点,
设直线的解析式为,
将代入,解得,
则直线的解析式为,
联立方程组,解得或(舍去),
则点.
②当时,,
则点,
设直线的函数解析式为,
把点、点代入,得,解得,
则直线的函数解析式为,
∴点,
那么,
∵,
∴,
∴,
(Ⅰ)若点在点上方,
过点作轴的平行线,交轴于点,如图,
∵,
∴轴,
∵轴,
∴点P与点Q重合,,
∴,
∴,
∴设,则,
∵轴,
∴,
∴,
则,
∵,
∴,
∴,
∴或(舍去),
∴.
把代入,得,
∴;
(Ⅱ)若点在点下方,
过点作轴,交的延长线于点,过点作的垂线,垂足为,交轴于点.如图,
∴,
∴四边形是矩形,
∴,
∵轴,
∴,,
∴ ,
∴设,则,
∵,,
∴,
又∵,
∴,
∴,
∴,,
则,,
那么,
代入,得,
∴(舍去),,
∴,
代入得,
∴.
综上所述,或.
同课章节目录
