20.1数据的集中趋势贴近中考特训 (含解析)2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 20.1数据的集中趋势贴近中考特训 (含解析)2023-2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 14:28:05 | ||
图片预览




文档简介
20.1 数据的集中趋势
一.选择题
1.(2023 黄石)我市某中学开展“经典诵读”比赛活动,810班在此次比赛中的得分分别是:9.1,9.8,9.1,9.2,9.9,9.1,9.9,9.1,这组数据的众数和中位数分别是( )
A.9.1,9.1 B.9.1,9.15 C.9.1,9.2 D.9.9,9.2
2.(2023 朝阳)学校篮球队队员进行定点投篮训练,每人投篮10次,其中5名队员投中的次数分别是:6,7,6,9,8,则这组数据的众数和中位数分别是( )
A.6,6 B.7,6 C.6,7 D.7,8
3.(2023 湘西州)某校九年级科技创新兴趣小组的7个成员体重(单位:kg)如下:38,42,35,40,36,42,75,则这组数据的众数和中位数分别是( )
A.42,36 B.42,42 C.40,40 D.42,40
4.(2023 盘锦)为了解全市中学生的视力情况,随机抽取某校50名学生的视力情况作为其中一个样本,整理样本数据如图.则这50名学生视力情况的中位数和众数分别是( )
A.4.8,4.8 B.13,13 C.4.7,13 D.13,4.8
5.(2023 鞍山)九(1)班30名同学在一次测试中,某道题目(满分4分)的得分情况如表:
得分/分 0 1 2 3 4
人数 1 3 4 14 8
则这道题目得分的众数和中位数分别是( )
A.8,3 B.8,2 C.3,3 D.3,2
6.(2023 锦州)在一次跳绳测试中,参与测试的10名学生一分钟跳绳成绩如下表所示:
成绩/次 129 130 132 135 137
人数/人 1 3 2 2 2
这10名学生跳绳成绩的中位数和众数分别为( )
A.132,130 B.132,132 C.130,130 D.130,132
7.(2023 宿迁)已知一组数据96,89,92,95,98,则这组数据的中位数是( )
A.89 B.94 C.95 D.98
8.(2023 娄底)一个小组7名同学的身高(单位:cm)分别为:175,160,158,155,168,151,170.这组数据的中位数是( )
A.151 B.155 C.158 D.160
9.(2023 辽宁)某校对部分参加夏令营的中学生的年龄进行统计,结果如下表:
年龄/岁 13 14 15 16 17 18
人数/人 5 8 11 20 9 7
则这些学生年龄的众数是( )
A.13岁 B.14岁 C.15岁 D.16岁
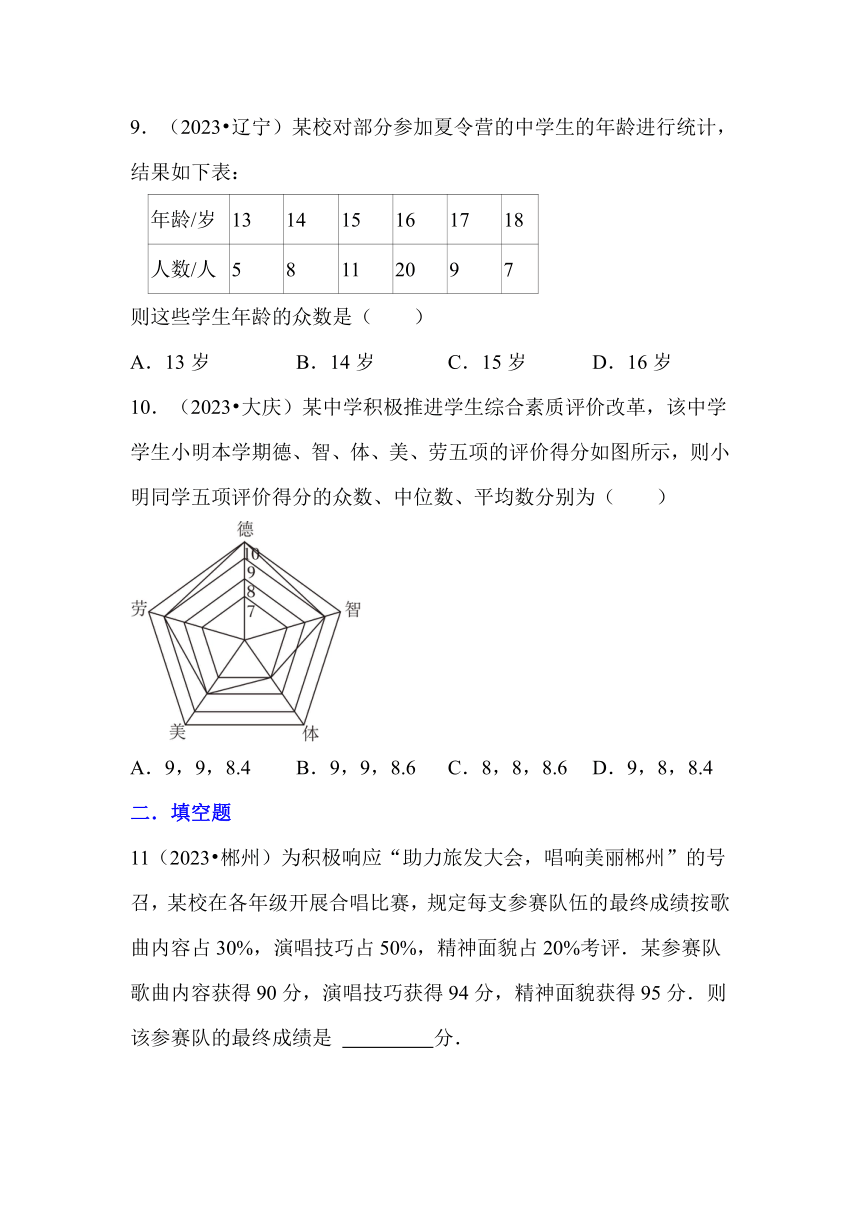
10.(2023 大庆)某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图所示,则小明同学五项评价得分的众数、中位数、平均数分别为( )
A.9,9,8.4 B.9,9,8.6 C.8,8,8.6 D.9,8,8.4
二.填空题
11(2023 郴州)为积极响应“助力旅发大会,唱响美丽郴州”的号召,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是 分.
12(2023 邵阳)下表是小红参加一次“阳光体育”活动比赛的得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占50%,花样跳绳占30%,跳绳占20%考评,则小红的最终得分为 .
13(2023 乐山)小张在“阳光大课间”活动中进行了5次一分钟跳绳练习,所跳个数分别为:160,163,160,157,160.这组数据的众数为 .
14(2023 湖北)眼睛是心灵的窗户,为保护学生视力,启航中学每学期给学生检查视力,下表是该校某班39名学生右眼视力的检查结果,这组视力数据中,中位数是 .
视力 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 2 6 3 3 4 1 2 5 7 5
15(2023 宜宾)在“庆五四 展风采”的演讲比赛中,7位同学参加决赛,演讲成绩依次为:77,80,79,77,80,79,80.这组数据的中位数是 .
16(2023 巴中)这组数据1,3,5,2,8,13的中位数是 .
17(2023 丽水)青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐,现有一农户在5块面积相等的稻田里养殖田鱼,产量分别是(单位:kg):12,13,15,17,18.则这5块稻田的田鱼平均产量是 kg.
三.解答题
18(2023 安徽)端午节是中国的传统节日,民间有端午节吃粽子的习俗.在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按10分制进行评分,成绩(单位:分)均为不低于6的整数.为了解这次活动的效果,现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理,并绘制统计图表,部分信息如下:
八年级10名学生活动成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 a b 2
已知八年级10名学生活动成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为7分的学生数是 ,七年级活动成绩的众数为 分;
(2)a= ,b= ;
(3)若认定活动成绩不低于9分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
19(2023 河北)某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,如图是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改;
(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?
20(2023 常德)党的二十大报告指出:“我们要全方位夯实粮食安全根基,牢牢守住十八亿亩耕地红线.确保中国人的饭碗牢牢端在自己手中”.为了了解粮食生产情况,某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下:
请根据图中信息回答下列问题:
(1)该种粮大户2022年早稻产量是 吨;
(2)2018年至2022年该种粮大户粮食总产量的中位数是 ,平均数是 ;
(3)该粮食大户估计2023年的粮食总产量年增长率与2022年的相同,那么2023年该粮食大户的粮食总产量是多少吨?
21(2023 常州)为合理安排进、离校时间,学校调查小组对某一天八年级学生上学、放学途中的用时情况进行了调查.本次调查在八年级随机抽取了20名学生,建立以上学途中用时为横坐标、放学途中用时为纵坐标的平面直角坐标系,并根据调查结果画出相应的点,如图所示:
(1)根据图中信息,下列说法中正确的是 (写出所有正确说法的序号);
①这20名学生上学途中用时都没有超过30min;
②这20名学生上学途中用时在20min以内的人数超过一半;
③这20名学生放学途中用时最短为5min;
④这20名学生放学途中用时的中位数为15min.
(2)已知该校八年级共有400名学生,请估计八年级学生上学途中用时超过25min的人数;
(3)调查小组发现,图中的点大致分布在一条直线附近.请直接写出这条直线对应的函数表达式并说明实际意义.
22(2023 衡阳)2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,80分及以上为优秀,共分成四组,A:60≤x<70;B:70≤x<80;C:80≤x<90;D:90≤x≤100),并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98 60%
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
23(2023 兰州)某校八年级共有男生300人,为了解该年级男生排球垫球成绩和掷实心球成绩的情况,从中随机抽取40名男生进行测试,对数据进行整理、描述和分析,下面是给出的部分信息.
信息一:排球垫球成绩如图所示(成绩用x表示,分成六组:A、x<10;B、10≤x<15;C、15≤x<20;D、20≤x<25;E、25≤x<30;F、30≤x).
信息二:排球垫球成绩在D、20≤x<25这一组的是:20,20,21,21,21,22,22,23,24,24;
信息三:掷实心球成绩(成绩用y表示,单位:米)的人数(频数)分布表如表:
分组 y<6.0 6.0≤y<6.8 6.8≤y<7.6 7.6≤y<8.4 8.4≤y<9.2 9.2≤y
人数 2 m 10 9 6 2
信息四:这次抽样测试中6名男生的两项成绩的部分数据如表:
学生 学生1 学生2 学生3 学生4 学生5 学生6
排球垫球 26 25 23 22 22 15
掷实心球 ▲ 7.8 7.8 ▲ 8.8 9.2
根据以上信息,回答下列问题:
(1)填空:m= ;
(2)下列结论正确的是 ;(填序号)
①排球垫球成绩超过10个的人数占抽取人数的百分比低于60%;
②掷实心球成绩的中位数记为n,则6.8≤n<7.6;
③若排球垫球成绩达到22个及以上时,成绩记为优秀,如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀;
(3)若排球垫球成绩达到22个及以上时,成绩记为优秀,请估计全年级男生排球垫球成绩达到优秀的人数.
答案
1【解答】解:将数据9.1,9.8,9.1,9.2,9.9,9.1,9.9,9.1按照从小到大排列是:9.1,9.1,9.1,9.1,9.2,9.8,9.9,9.9,
则这组数据的众数是9.1,中位数是(9.1+9.2)÷2=9.15,
故选:B.
2【解答】解:投中次数6的人数最多,故众数是6;
共有数据5个,由小到大排序后第3个数是7,所以中位数是7.
故选:C.
3【解答】解:出现次数最多的数据为42,
∴众数为42,
排序后,位于中间位置的数据为40,
∴中位数为40;
故选:D.
4【解答】解:把这50名学生视力情况从小到大排列,排在中间的两个数分别是4.8、4.8,故中位数为4.8;
在这50名学生视力情况中,4.8出现的次数最多,故众数为4.8.
故选:A.
5【解答】解:这30名学生测试成绩出现次数最多的是3分,共出现14次,因此学生测试成绩的众数是3,
将这30名学生测试成绩从小到大排列,处在中间位置的两个数都是3分,因此中位数是3,
故选:C.
6【解答】解:从小到大排列此数据为:129、130、130、130、132、132、135、135、137、137,
数据130出现了三次最多为众数,
中位数为:132,
所以本题这组数据的中位数是132,众数是130.
故选:A.
7【解答】解:把数据从小到大的顺序排列为:89,92,95,96,98,
∴中位数为95.
故选:C.
8【解答】解:把这些数从小到大排列为:151、155、158、160、168、170、175,
排在中间的数为160,故中位数为160.
故选:D.
9【解答】解:∵在这一组数据中16是出现次数最多的,出现了20次,
∴这些学生年龄的众数是16岁;
故选:D.
10【解答】解:该同学五项评价得分从小到大排列分别为7,8,9,9,10,
出现次数最多的数是9,所以众数为9,
位于中间位置的数是8,所以中位数是9,
平均数为(7+8+9+9+10)=8.6
故选:B.
11【解答】解:根据题意,该参赛队的最终成绩是:30%×90+20%×95+50%×94=93(分).
故答案为:93.
12【解答】解:小红的最终得分为:90×50%+80×30%+70×20%=83(分).
故答案为:83分.
13【解答】解:由题意知,这组数据中160出现3次,次数最多,
所以这组数据的众数为160,
故答案为:160.
14【解答】解:将这组数据从小到大的顺序排列后,位于最中间的一个数是4.6,
所以中位数是4.6.
故答案为:4.6.
15【解答】解:将这组数据从小到大排列为:77,77,79,79,80,80,80,位置在中间的数是79,
∴这组数据的中位数是79;
故答案为:79.
16【解答】解:将这组数据重新排列为1,2,3,5,8,13,
所以这组数据的中位数为(3+5)=4,
故答案为:4.
17【解答】解:(12+13+15+17+18)÷5
=75÷5
=15(kg).
答:这5块稻田的田鱼平均产量是15kg.
故答案为:15.
18【解答】解:(1)由扇形统计图可得,成绩为8分的人数为10×50%=5(人),
成绩为9分的人数为10×20%=2(人),
成绩为10分的人数为10×20%=2(人),
则成绩为7分的学生数为10﹣5﹣2﹣2=1(人),
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分,
故答案为:1;8;
(2)由题意,将八年级的活动成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵八年级10名学生活动成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),成绩为9分的人数为10﹣5﹣2=3(人),
即a=2,b=3,
故答案为:2;3;
(3)不是,理由如下:
结合(1)(2)中所求可得七年级的优秀率为100%=40%,八年级的优秀率为100%=50%,
七年级的平均成绩为8.5(分),八年级的平均成绩为8.3(分),
∵40%<50%,8.5>8.3,
∴本次活动中优秀率高的年级并不是平均成绩也高.
19【解答】解:(1)由条形图可知,第10个数据是3分,第11个数据是4分,
∴中位数为3.5分,
由统计图可得平均数为3.5分,
∴客户所评分数的平均数或中位数都不低于3.5分,
∴该部门不需要整改.
(2)监督人员抽取的问卷所评分数为x分,则有
,
解得x>4.55,
∵满意度从低到高为1分,2分,3分,4分,5分,共5档.
∴监督人员抽取的问卷所评分数为5分,
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列后,第11个数据不变还是4分,即加入这个数据后,中位数是4分,
∴与(1)相比,中位数是发生了变化,由3.5分变成4分.
20【解答】解:(1)250×(1﹣75%﹣21%)=10(吨).
故答案为:10;
(2)将5个数据按从小到大的顺序排列后,第三个数为160,所以中位数为160吨;
(120+140+160+200+250)÷5=174(吨).
故答案为:160吨;174吨;
(3)(250﹣200)÷200×100%=25%,
250×(1+25%)=312.5(吨).
即2023年该粮食大户的粮食总产量是312.5吨.
21【解答】解:(1)根据在坐标系中点的位置,可知:
这20名学生上学途中用时最长的时间为30min,故①说法正确;
这20名学生上学途中用时在20min以内的人数为:17人,超过一半,故②说法正确;
这20名学生放学途中用时最段的时间为5min,故③说法正确;
这20名学生放学途中用时的中位数是用时第10和第11的两名学生用时的平均数,在图中,用时第10和第11的两名学生的用时均小于15min,故这20名学生放学途中用时的中位数为也小于15min,即④说法错误;
故答案为:①②③.
(2)根据图中信息可知,上学途中用时超过25min的学生有1人,
故该校八年级学生上学途中用时超过25min的人数为400×120=20(人).
(3)如图:
设直线的解析式为:y=kx+b,根据图象可得,直线经过点(10,10),(7,7),
将(10,10),(7,7)代入y=kx+b,得:
,
解得:,
故直线的解析式为:y=x;
则这条直线可近似反映学生上学途中用时和放学途中用时一样.
22【解答】解:(1)八年级的竞赛成绩从小到大排列后,处在中间位置的一个数是84,因此中位数是84,即a=84;
九年级的竞赛成绩出现次数最多的是100,共出现3次,因此众数是100,即b=100;
九年级的竞赛成绩中80分及以上的共有12人,因此优秀率为100%=80%,即c=80%;
故答案为:84,100,80%;
(2)500200(人),
答:估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数约200人.
23【解答】解:(1)m=40﹣2﹣10﹣9﹣6﹣2=11,
故答案为:11;
(2)由条形统计图可得,排球垫球成绩超过10个的人数占抽取人数的百分比:65%,①错误.
掷实心球成绩的中位数记为n,则6.8≤n<7.6,②正确.
若排球垫球成绩达到22个及以上时,成绩记为优秀,如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀.
理由:如果学生3的掷实心球的成绩未到达优秀,那么只有学生1、4、5、6有可能两项测试成绩都达到优秀,这与恰有4个人两项成绩都达到优秀,矛盾,③正确.
故答案为:②③;
(2)∵排球垫球成绩达到22个及以上的人数:10人,
∴全年级男生排球垫球成绩达到优秀的人数是:30075,
答:估计全年级男生排球垫球成绩达到优秀的人数是有75人.
一.选择题
1.(2023 黄石)我市某中学开展“经典诵读”比赛活动,810班在此次比赛中的得分分别是:9.1,9.8,9.1,9.2,9.9,9.1,9.9,9.1,这组数据的众数和中位数分别是( )
A.9.1,9.1 B.9.1,9.15 C.9.1,9.2 D.9.9,9.2
2.(2023 朝阳)学校篮球队队员进行定点投篮训练,每人投篮10次,其中5名队员投中的次数分别是:6,7,6,9,8,则这组数据的众数和中位数分别是( )
A.6,6 B.7,6 C.6,7 D.7,8
3.(2023 湘西州)某校九年级科技创新兴趣小组的7个成员体重(单位:kg)如下:38,42,35,40,36,42,75,则这组数据的众数和中位数分别是( )
A.42,36 B.42,42 C.40,40 D.42,40
4.(2023 盘锦)为了解全市中学生的视力情况,随机抽取某校50名学生的视力情况作为其中一个样本,整理样本数据如图.则这50名学生视力情况的中位数和众数分别是( )
A.4.8,4.8 B.13,13 C.4.7,13 D.13,4.8
5.(2023 鞍山)九(1)班30名同学在一次测试中,某道题目(满分4分)的得分情况如表:
得分/分 0 1 2 3 4
人数 1 3 4 14 8
则这道题目得分的众数和中位数分别是( )
A.8,3 B.8,2 C.3,3 D.3,2
6.(2023 锦州)在一次跳绳测试中,参与测试的10名学生一分钟跳绳成绩如下表所示:
成绩/次 129 130 132 135 137
人数/人 1 3 2 2 2
这10名学生跳绳成绩的中位数和众数分别为( )
A.132,130 B.132,132 C.130,130 D.130,132
7.(2023 宿迁)已知一组数据96,89,92,95,98,则这组数据的中位数是( )
A.89 B.94 C.95 D.98
8.(2023 娄底)一个小组7名同学的身高(单位:cm)分别为:175,160,158,155,168,151,170.这组数据的中位数是( )
A.151 B.155 C.158 D.160
9.(2023 辽宁)某校对部分参加夏令营的中学生的年龄进行统计,结果如下表:
年龄/岁 13 14 15 16 17 18
人数/人 5 8 11 20 9 7
则这些学生年龄的众数是( )
A.13岁 B.14岁 C.15岁 D.16岁
10.(2023 大庆)某中学积极推进学生综合素质评价改革,该中学学生小明本学期德、智、体、美、劳五项的评价得分如图所示,则小明同学五项评价得分的众数、中位数、平均数分别为( )
A.9,9,8.4 B.9,9,8.6 C.8,8,8.6 D.9,8,8.4
二.填空题
11(2023 郴州)为积极响应“助力旅发大会,唱响美丽郴州”的号召,某校在各年级开展合唱比赛,规定每支参赛队伍的最终成绩按歌曲内容占30%,演唱技巧占50%,精神面貌占20%考评.某参赛队歌曲内容获得90分,演唱技巧获得94分,精神面貌获得95分.则该参赛队的最终成绩是 分.
12(2023 邵阳)下表是小红参加一次“阳光体育”活动比赛的得分情况:
项目 跑步 花样跳绳 跳绳
得分 90 80 70
评总分时,按跑步占50%,花样跳绳占30%,跳绳占20%考评,则小红的最终得分为 .
13(2023 乐山)小张在“阳光大课间”活动中进行了5次一分钟跳绳练习,所跳个数分别为:160,163,160,157,160.这组数据的众数为 .
14(2023 湖北)眼睛是心灵的窗户,为保护学生视力,启航中学每学期给学生检查视力,下表是该校某班39名学生右眼视力的检查结果,这组视力数据中,中位数是 .
视力 4.0 4.1 4.2 4.3 4.4 4.5 4.6 4.7 4.8 4.9 5.0
人数 1 2 6 3 3 4 1 2 5 7 5
15(2023 宜宾)在“庆五四 展风采”的演讲比赛中,7位同学参加决赛,演讲成绩依次为:77,80,79,77,80,79,80.这组数据的中位数是 .
16(2023 巴中)这组数据1,3,5,2,8,13的中位数是 .
17(2023 丽水)青田县“稻鱼共生”种养方式因稻鱼双收、互惠共生而受到农户青睐,现有一农户在5块面积相等的稻田里养殖田鱼,产量分别是(单位:kg):12,13,15,17,18.则这5块稻田的田鱼平均产量是 kg.
三.解答题
18(2023 安徽)端午节是中国的传统节日,民间有端午节吃粽子的习俗.在端午节来临之际,某校七、八年级开展了一次“包粽子”实践活动,对学生的活动情况按10分制进行评分,成绩(单位:分)均为不低于6的整数.为了解这次活动的效果,现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理,并绘制统计图表,部分信息如下:
八年级10名学生活动成绩统计表
成绩/分 6 7 8 9 10
人数 1 2 a b 2
已知八年级10名学生活动成绩的中位数为8.5分.
请根据以上信息,完成下列问题:
(1)样本中,七年级活动成绩为7分的学生数是 ,七年级活动成绩的众数为 分;
(2)a= ,b= ;
(3)若认定活动成绩不低于9分为“优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
19(2023 河北)某公司为提高服务质量,对其某个部门开展了客户满意度问卷调查,客户满意度以分数呈现,满意度从低到高为1分,2分,3分,4分,5分,共5档.公司规定:若客户所评分数的平均数或中位数低于3.5分,则该部门需要对服务质量进行整改.工作人员从收回的问卷中随机抽取了20份,如图是根据这20份问卷中的客户所评分数绘制的统计图.
(1)求客户所评分数的中位数、平均数,并判断该部门是否需要整改;
(2)监督人员从余下的问卷中又随机抽取了1份,与之前的20份合在一起,重新计算后,发现客户所评分数的平均数大于3.55分,求监督人员抽取的问卷所评分数为几分?与(1)相比,中位数是否发生变化?
20(2023 常德)党的二十大报告指出:“我们要全方位夯实粮食安全根基,牢牢守住十八亿亩耕地红线.确保中国人的饭碗牢牢端在自己手中”.为了了解粮食生产情况,某校数学兴趣小组调查了某种粮大户2018年至2022年粮食总产量及2022年粮食分季节占比情况如下:
请根据图中信息回答下列问题:
(1)该种粮大户2022年早稻产量是 吨;
(2)2018年至2022年该种粮大户粮食总产量的中位数是 ,平均数是 ;
(3)该粮食大户估计2023年的粮食总产量年增长率与2022年的相同,那么2023年该粮食大户的粮食总产量是多少吨?
21(2023 常州)为合理安排进、离校时间,学校调查小组对某一天八年级学生上学、放学途中的用时情况进行了调查.本次调查在八年级随机抽取了20名学生,建立以上学途中用时为横坐标、放学途中用时为纵坐标的平面直角坐标系,并根据调查结果画出相应的点,如图所示:
(1)根据图中信息,下列说法中正确的是 (写出所有正确说法的序号);
①这20名学生上学途中用时都没有超过30min;
②这20名学生上学途中用时在20min以内的人数超过一半;
③这20名学生放学途中用时最短为5min;
④这20名学生放学途中用时的中位数为15min.
(2)已知该校八年级共有400名学生,请估计八年级学生上学途中用时超过25min的人数;
(3)调查小组发现,图中的点大致分布在一条直线附近.请直接写出这条直线对应的函数表达式并说明实际意义.
22(2023 衡阳)2023年3月27日是第28个全国中小学生安全教育日,为提高学生安全防范意识和自我防护能力,某学校举行了校园安全知识竞赛活动.现从八、九年级中各随机抽取15名学生的竞赛成绩(百分制)进行整理、描述和分析(成绩得分用x表示,80分及以上为优秀,共分成四组,A:60≤x<70;B:70≤x<80;C:80≤x<90;D:90≤x≤100),并给出下面部分信息:
八年级抽取的学生竞赛成绩在C组中的数据为:84,84,88
九年级抽取的学生竞赛成绩为:68,77,75,100,80,100,82,86,95,91,100,86,84,94,87.
八、九年级抽取的学生竞赛成绩统计表
年级 平均数 中位数 众数 优秀率
八 87 a 98 60%
九 87 86 b c
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,c= ;
(2)该校八、九年级共500人参加了此次竞赛活动,请你估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数.
23(2023 兰州)某校八年级共有男生300人,为了解该年级男生排球垫球成绩和掷实心球成绩的情况,从中随机抽取40名男生进行测试,对数据进行整理、描述和分析,下面是给出的部分信息.
信息一:排球垫球成绩如图所示(成绩用x表示,分成六组:A、x<10;B、10≤x<15;C、15≤x<20;D、20≤x<25;E、25≤x<30;F、30≤x).
信息二:排球垫球成绩在D、20≤x<25这一组的是:20,20,21,21,21,22,22,23,24,24;
信息三:掷实心球成绩(成绩用y表示,单位:米)的人数(频数)分布表如表:
分组 y<6.0 6.0≤y<6.8 6.8≤y<7.6 7.6≤y<8.4 8.4≤y<9.2 9.2≤y
人数 2 m 10 9 6 2
信息四:这次抽样测试中6名男生的两项成绩的部分数据如表:
学生 学生1 学生2 学生3 学生4 学生5 学生6
排球垫球 26 25 23 22 22 15
掷实心球 ▲ 7.8 7.8 ▲ 8.8 9.2
根据以上信息,回答下列问题:
(1)填空:m= ;
(2)下列结论正确的是 ;(填序号)
①排球垫球成绩超过10个的人数占抽取人数的百分比低于60%;
②掷实心球成绩的中位数记为n,则6.8≤n<7.6;
③若排球垫球成绩达到22个及以上时,成绩记为优秀,如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀;
(3)若排球垫球成绩达到22个及以上时,成绩记为优秀,请估计全年级男生排球垫球成绩达到优秀的人数.
答案
1【解答】解:将数据9.1,9.8,9.1,9.2,9.9,9.1,9.9,9.1按照从小到大排列是:9.1,9.1,9.1,9.1,9.2,9.8,9.9,9.9,
则这组数据的众数是9.1,中位数是(9.1+9.2)÷2=9.15,
故选:B.
2【解答】解:投中次数6的人数最多,故众数是6;
共有数据5个,由小到大排序后第3个数是7,所以中位数是7.
故选:C.
3【解答】解:出现次数最多的数据为42,
∴众数为42,
排序后,位于中间位置的数据为40,
∴中位数为40;
故选:D.
4【解答】解:把这50名学生视力情况从小到大排列,排在中间的两个数分别是4.8、4.8,故中位数为4.8;
在这50名学生视力情况中,4.8出现的次数最多,故众数为4.8.
故选:A.
5【解答】解:这30名学生测试成绩出现次数最多的是3分,共出现14次,因此学生测试成绩的众数是3,
将这30名学生测试成绩从小到大排列,处在中间位置的两个数都是3分,因此中位数是3,
故选:C.
6【解答】解:从小到大排列此数据为:129、130、130、130、132、132、135、135、137、137,
数据130出现了三次最多为众数,
中位数为:132,
所以本题这组数据的中位数是132,众数是130.
故选:A.
7【解答】解:把数据从小到大的顺序排列为:89,92,95,96,98,
∴中位数为95.
故选:C.
8【解答】解:把这些数从小到大排列为:151、155、158、160、168、170、175,
排在中间的数为160,故中位数为160.
故选:D.
9【解答】解:∵在这一组数据中16是出现次数最多的,出现了20次,
∴这些学生年龄的众数是16岁;
故选:D.
10【解答】解:该同学五项评价得分从小到大排列分别为7,8,9,9,10,
出现次数最多的数是9,所以众数为9,
位于中间位置的数是8,所以中位数是9,
平均数为(7+8+9+9+10)=8.6
故选:B.
11【解答】解:根据题意,该参赛队的最终成绩是:30%×90+20%×95+50%×94=93(分).
故答案为:93.
12【解答】解:小红的最终得分为:90×50%+80×30%+70×20%=83(分).
故答案为:83分.
13【解答】解:由题意知,这组数据中160出现3次,次数最多,
所以这组数据的众数为160,
故答案为:160.
14【解答】解:将这组数据从小到大的顺序排列后,位于最中间的一个数是4.6,
所以中位数是4.6.
故答案为:4.6.
15【解答】解:将这组数据从小到大排列为:77,77,79,79,80,80,80,位置在中间的数是79,
∴这组数据的中位数是79;
故答案为:79.
16【解答】解:将这组数据重新排列为1,2,3,5,8,13,
所以这组数据的中位数为(3+5)=4,
故答案为:4.
17【解答】解:(12+13+15+17+18)÷5
=75÷5
=15(kg).
答:这5块稻田的田鱼平均产量是15kg.
故答案为:15.
18【解答】解:(1)由扇形统计图可得,成绩为8分的人数为10×50%=5(人),
成绩为9分的人数为10×20%=2(人),
成绩为10分的人数为10×20%=2(人),
则成绩为7分的学生数为10﹣5﹣2﹣2=1(人),
∵出现次数最多的为8分,
∴七年级活动成绩的众数为8分,
故答案为:1;8;
(2)由题意,将八年级的活动成绩从小到大排列后,它的中位数应是第5个和第6个数据的平均数,
∵八年级10名学生活动成绩的中位数为8.5分,
∴第5个和第6个数据的和为8.5×2=17=8+9,
∴第5个和第6个数据分别为8分,9分,
∵成绩为6分和7分的人数为1+2=3(人),
∴成绩为8分的人数为5﹣3=2(人),成绩为9分的人数为10﹣5﹣2=3(人),
即a=2,b=3,
故答案为:2;3;
(3)不是,理由如下:
结合(1)(2)中所求可得七年级的优秀率为100%=40%,八年级的优秀率为100%=50%,
七年级的平均成绩为8.5(分),八年级的平均成绩为8.3(分),
∵40%<50%,8.5>8.3,
∴本次活动中优秀率高的年级并不是平均成绩也高.
19【解答】解:(1)由条形图可知,第10个数据是3分,第11个数据是4分,
∴中位数为3.5分,
由统计图可得平均数为3.5分,
∴客户所评分数的平均数或中位数都不低于3.5分,
∴该部门不需要整改.
(2)监督人员抽取的问卷所评分数为x分,则有
,
解得x>4.55,
∵满意度从低到高为1分,2分,3分,4分,5分,共5档.
∴监督人员抽取的问卷所评分数为5分,
∵4<5,
∴加入这个数据,客户所评分数按从小到大排列后,第11个数据不变还是4分,即加入这个数据后,中位数是4分,
∴与(1)相比,中位数是发生了变化,由3.5分变成4分.
20【解答】解:(1)250×(1﹣75%﹣21%)=10(吨).
故答案为:10;
(2)将5个数据按从小到大的顺序排列后,第三个数为160,所以中位数为160吨;
(120+140+160+200+250)÷5=174(吨).
故答案为:160吨;174吨;
(3)(250﹣200)÷200×100%=25%,
250×(1+25%)=312.5(吨).
即2023年该粮食大户的粮食总产量是312.5吨.
21【解答】解:(1)根据在坐标系中点的位置,可知:
这20名学生上学途中用时最长的时间为30min,故①说法正确;
这20名学生上学途中用时在20min以内的人数为:17人,超过一半,故②说法正确;
这20名学生放学途中用时最段的时间为5min,故③说法正确;
这20名学生放学途中用时的中位数是用时第10和第11的两名学生用时的平均数,在图中,用时第10和第11的两名学生的用时均小于15min,故这20名学生放学途中用时的中位数为也小于15min,即④说法错误;
故答案为:①②③.
(2)根据图中信息可知,上学途中用时超过25min的学生有1人,
故该校八年级学生上学途中用时超过25min的人数为400×120=20(人).
(3)如图:
设直线的解析式为:y=kx+b,根据图象可得,直线经过点(10,10),(7,7),
将(10,10),(7,7)代入y=kx+b,得:
,
解得:,
故直线的解析式为:y=x;
则这条直线可近似反映学生上学途中用时和放学途中用时一样.
22【解答】解:(1)八年级的竞赛成绩从小到大排列后,处在中间位置的一个数是84,因此中位数是84,即a=84;
九年级的竞赛成绩出现次数最多的是100,共出现3次,因此众数是100,即b=100;
九年级的竞赛成绩中80分及以上的共有12人,因此优秀率为100%=80%,即c=80%;
故答案为:84,100,80%;
(2)500200(人),
答:估计该校八、九年级参加此次竞赛活动成绩达到90分及以上的学生人数约200人.
23【解答】解:(1)m=40﹣2﹣10﹣9﹣6﹣2=11,
故答案为:11;
(2)由条形统计图可得,排球垫球成绩超过10个的人数占抽取人数的百分比:65%,①错误.
掷实心球成绩的中位数记为n,则6.8≤n<7.6,②正确.
若排球垫球成绩达到22个及以上时,成绩记为优秀,如果信息四中6名男生的两项成绩恰好为优秀的有4名,那么学生3掷实心球的成绩是优秀.
理由:如果学生3的掷实心球的成绩未到达优秀,那么只有学生1、4、5、6有可能两项测试成绩都达到优秀,这与恰有4个人两项成绩都达到优秀,矛盾,③正确.
故答案为:②③;
(2)∵排球垫球成绩达到22个及以上的人数:10人,
∴全年级男生排球垫球成绩达到优秀的人数是:30075,
答:估计全年级男生排球垫球成绩达到优秀的人数是有75人.
