2024年中考数学专题复习:锐角三角函数(含答案)
文档属性
| 名称 | 2024年中考数学专题复习:锐角三角函数(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 305.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 14:37:30 | ||
图片预览

文档简介
2024年中考数学专题复习:锐角三角函数
一、单选题
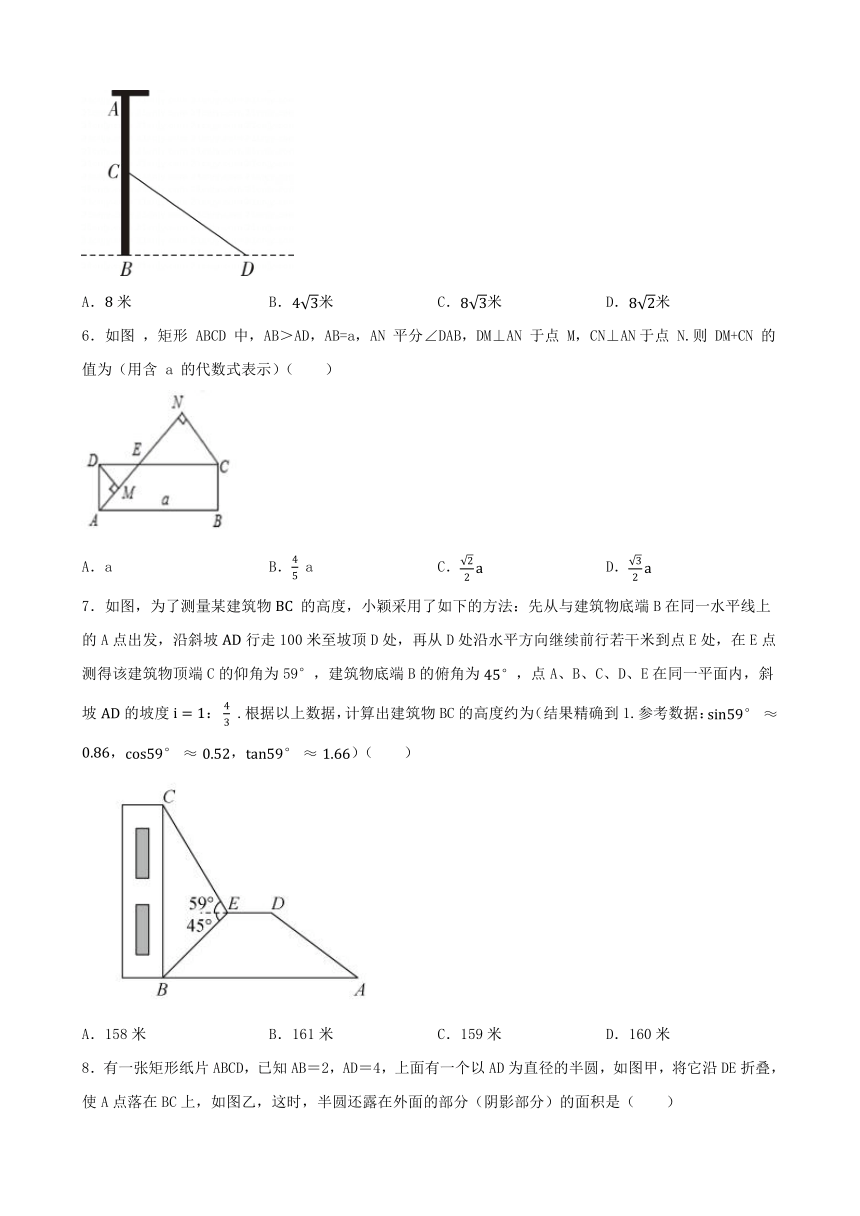
1.已知一个坡的坡比为i,坡角为α,则下列等式成立的是( )
A.i=sinα B.i=cosα C.i=tanα D.i=cotα
2.如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=A,则A、B两点的距离为( )
A.asinA B.acosA C.atanA D.
3.如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A.3 B. C.4 D.
4.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,是格点三角形,则的值为( )
A. B. C. D.
5. 如图,电线杆的中点处有一标志物,在地面处测得标志物的仰角为,若到电线杆底部的距离为米,则电线杆的长为( )
A.米 B.米 C.米 D.米
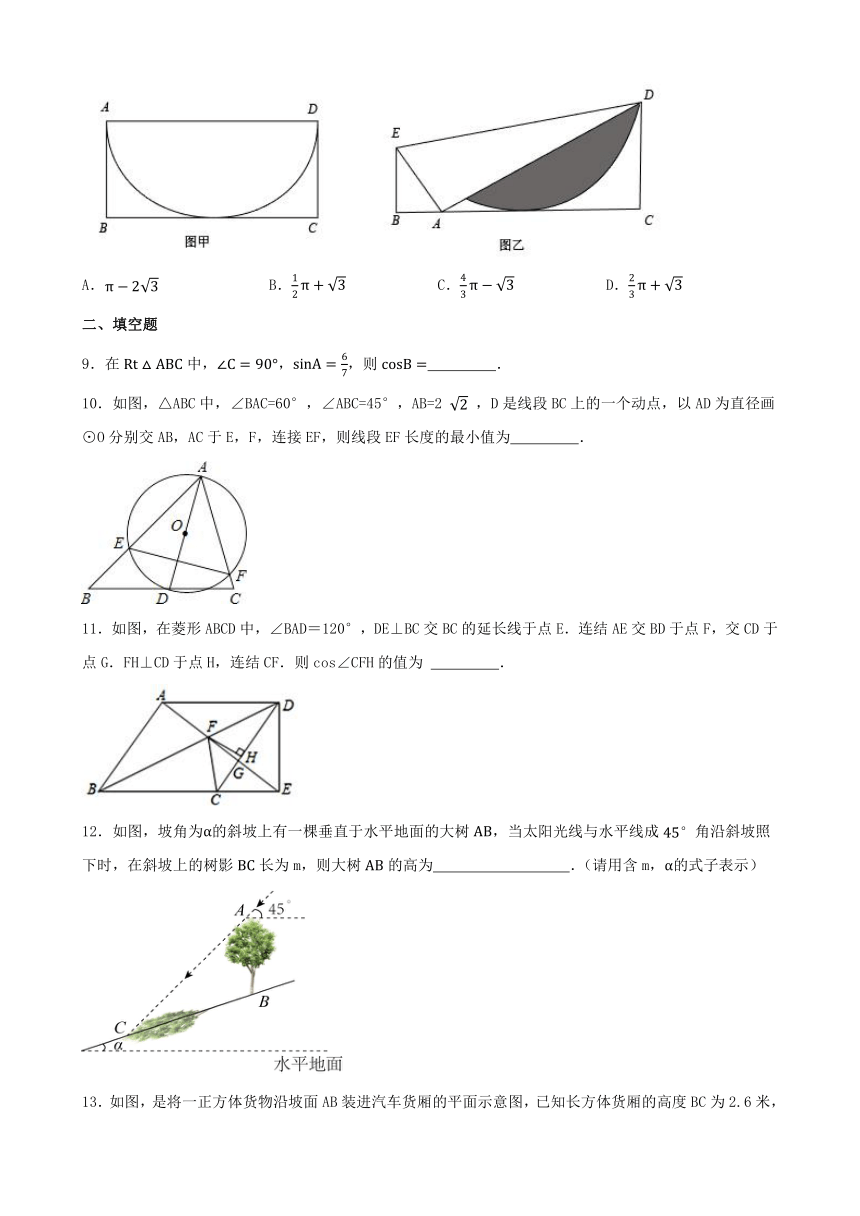
6.如图 ,矩形 ABCD 中,AB>AD,AB=a,AN 平分∠DAB,DM⊥AN 于点 M,CN⊥AN于点 N.则 DM+CN 的值为(用含 a 的代数式表示)( )
A.a B. a C. D.
7.如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为,点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据:,,)( )
A.158米 B.161米 C.159米 D.160米
8.有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )
A. B. C. D.
二、填空题
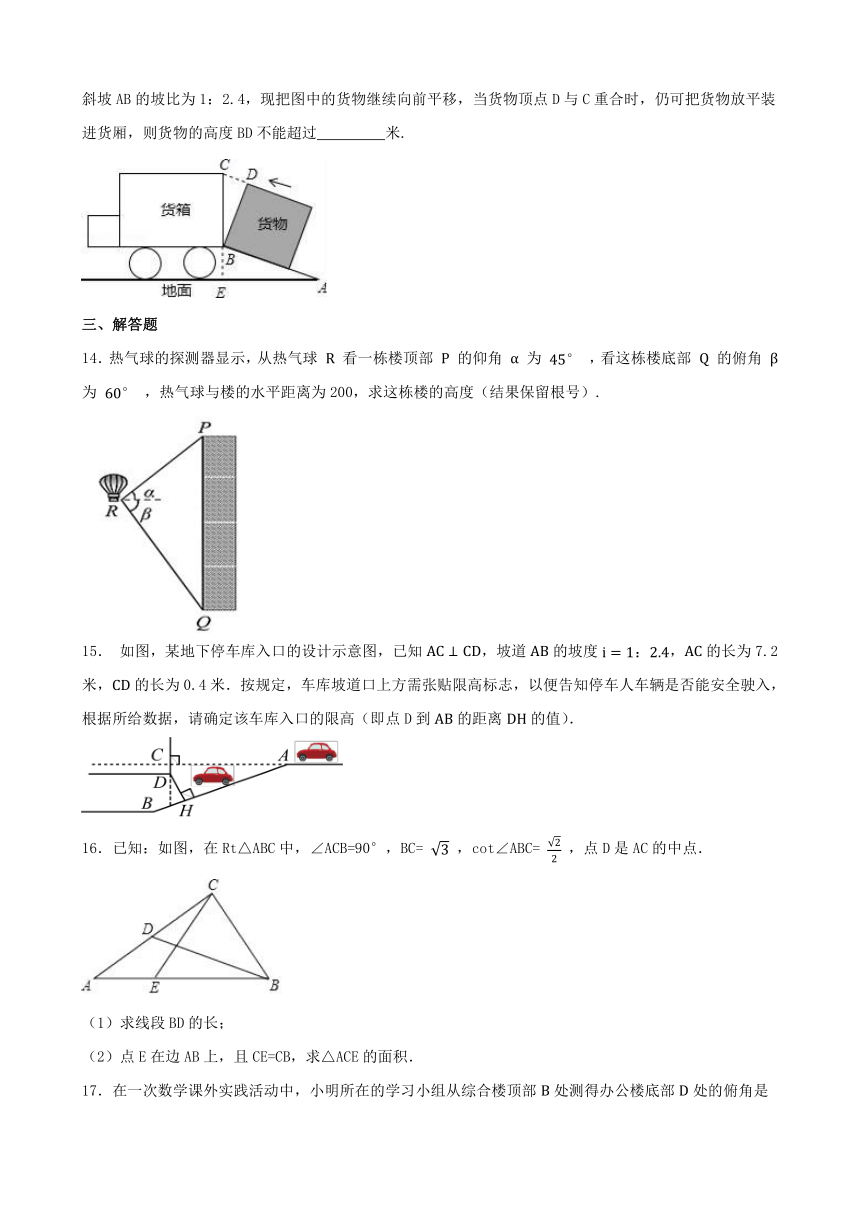
9.在中,,,则 .
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
11.如图,在菱形ABCD中,∠BAD=120°,DE⊥BC交BC的延长线于点E.连结AE交BD于点F,交CD于点G.FH⊥CD于点H,连结CF.则cos∠CFH的值为 .
12.如图,坡角为的斜坡上有一棵垂直于水平地面的大树,当太阳光线与水平线成角沿斜坡照下时,在斜坡上的树影长为m,则大树的高为 .(请用含m,的式子表示)
13.如图,是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6米,斜坡AB的坡比为1:2.4,现把图中的货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过 米.
三、解答题
14.热气球的探测器显示,从热气球 看一栋楼顶部 的仰角 为 ,看这栋楼底部 的俯角 为 ,热气球与楼的水平距离为200,求这栋楼的高度(结果保留根号).
15. 如图,某地下停车库入口的设计示意图,已知,坡道的坡度,的长为7.2米,的长为0.4米.按规定,车库坡道口上方需张贴限高标志,以便告知停车人车辆是否能安全驶入,根据所给数据,请确定该车库入口的限高(即点D到的距离的值).
16.已知:如图,在Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
17.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部处测得办公楼底部处的俯角是,从综合楼底部处测得办公楼顶部处的仰角恰好是,综合楼高米请你帮小明求出办公楼的高度结果精确到,参考数据,,
18.如图,在平面直角坐标系xOy中,点 , 在反比例函数 (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点 ,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证:
答案
1.C
2.C
3.D
4.A
5.C
6.C
7.D
8.C
9.
10.
11.
12.
13.2.4
14.解:过点 作 ,垂足为 ,
则 .
在 中,∵ ,
∴ .
在 中,∵ ,
∴ .
∴ .
答:这栋楼的高度为 .
15.解:解:如图:
延长交于E,
,
∴,
,
,
过点D作于H,
,
,
(米).
答:该车库入口的限高为2.4米.
16.(1)解:Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,∴AC= ,∵点D是AC的中点,
∴CD= AC= ,
∴Rt△BCD中,BD= =
(2)解:如图,过C作CH⊥AB于H,∵BC= ,cot∠ABC= ,
∴CH= ,BH=1,
∵CE=CB,
∴EH=BH=1,
∵∠ACB=90°,BC= ,AC= ,
∴AB=3,
∴AE=3﹣2=1,
∴△ACE的面积= ×AE×CH= ×1× = .
17.解:由题意可知米,,
,
.
,
米.
故办公楼的高度约为米.
18.(1)解:∵点A( ,2)在反比例函数 (m为常数)的图象上,
∴m= ×2=1,
∴反比例函数 (m为常数)对应的函数表达式是 .
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A( ,2),D(1,0),
∴ ,解得: ,
∴直线l对应的函数表达式为y=﹣4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣ ,﹣2).
∵CE∥x轴交直线l于点E,∴yE=yC,∴点E的坐标为E( ,﹣2).
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,
∵点B(3,n)在反比例函数图象上,
∴n= ,
∴B(3, ),G( , ),H(﹣ , ).
在Rt△ABG中,tan∠ABH= ,
在Rt△BCH中,tan∠CBH= ,
∴tan∠ABN=tan∠CBN
一、单选题
1.已知一个坡的坡比为i,坡角为α,则下列等式成立的是( )
A.i=sinα B.i=cosα C.i=tanα D.i=cotα
2.如图,为测量河两岸A、B距离,在与AB垂直方向取点C,测得AC=a,∠ACB=A,则A、B两点的距离为( )
A.asinA B.acosA C.atanA D.
3.如图,已知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为( )
A.3 B. C.4 D.
4.在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,是格点三角形,则的值为( )
A. B. C. D.
5. 如图,电线杆的中点处有一标志物,在地面处测得标志物的仰角为,若到电线杆底部的距离为米,则电线杆的长为( )
A.米 B.米 C.米 D.米
6.如图 ,矩形 ABCD 中,AB>AD,AB=a,AN 平分∠DAB,DM⊥AN 于点 M,CN⊥AN于点 N.则 DM+CN 的值为(用含 a 的代数式表示)( )
A.a B. a C. D.
7.如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端B在同一水平线上的A点出发,沿斜坡行走100米至坡顶D处,再从D处沿水平方向继续前行若干米到点E处,在E点测得该建筑物顶端C的仰角为59°,建筑物底端B的俯角为,点A、B、C、D、E在同一平面内,斜坡的坡度 .根据以上数据,计算出建筑物BC的高度约为(结果精确到1.参考数据:,,)( )
A.158米 B.161米 C.159米 D.160米
8.有一张矩形纸片ABCD,已知AB=2,AD=4,上面有一个以AD为直径的半圆,如图甲,将它沿DE折叠,使A点落在BC上,如图乙,这时,半圆还露在外面的部分(阴影部分)的面积是( )
A. B. C. D.
二、填空题
9.在中,,,则 .
10.如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为 .
11.如图,在菱形ABCD中,∠BAD=120°,DE⊥BC交BC的延长线于点E.连结AE交BD于点F,交CD于点G.FH⊥CD于点H,连结CF.则cos∠CFH的值为 .
12.如图,坡角为的斜坡上有一棵垂直于水平地面的大树,当太阳光线与水平线成角沿斜坡照下时,在斜坡上的树影长为m,则大树的高为 .(请用含m,的式子表示)
13.如图,是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6米,斜坡AB的坡比为1:2.4,现把图中的货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过 米.
三、解答题
14.热气球的探测器显示,从热气球 看一栋楼顶部 的仰角 为 ,看这栋楼底部 的俯角 为 ,热气球与楼的水平距离为200,求这栋楼的高度(结果保留根号).
15. 如图,某地下停车库入口的设计示意图,已知,坡道的坡度,的长为7.2米,的长为0.4米.按规定,车库坡道口上方需张贴限高标志,以便告知停车人车辆是否能安全驶入,根据所给数据,请确定该车库入口的限高(即点D到的距离的值).
16.已知:如图,在Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
17.在一次数学课外实践活动中,小明所在的学习小组从综合楼顶部处测得办公楼底部处的俯角是,从综合楼底部处测得办公楼顶部处的仰角恰好是,综合楼高米请你帮小明求出办公楼的高度结果精确到,参考数据,,
18.如图,在平面直角坐标系xOy中,点 , 在反比例函数 (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点 ,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证:
答案
1.C
2.C
3.D
4.A
5.C
6.C
7.D
8.C
9.
10.
11.
12.
13.2.4
14.解:过点 作 ,垂足为 ,
则 .
在 中,∵ ,
∴ .
在 中,∵ ,
∴ .
∴ .
答:这栋楼的高度为 .
15.解:解:如图:
延长交于E,
,
∴,
,
,
过点D作于H,
,
,
(米).
答:该车库入口的限高为2.4米.
16.(1)解:Rt△ABC中,∠ACB=90°,BC= ,cot∠ABC= ,∴AC= ,∵点D是AC的中点,
∴CD= AC= ,
∴Rt△BCD中,BD= =
(2)解:如图,过C作CH⊥AB于H,∵BC= ,cot∠ABC= ,
∴CH= ,BH=1,
∵CE=CB,
∴EH=BH=1,
∵∠ACB=90°,BC= ,AC= ,
∴AB=3,
∴AE=3﹣2=1,
∴△ACE的面积= ×AE×CH= ×1× = .
17.解:由题意可知米,,
,
.
,
米.
故办公楼的高度约为米.
18.(1)解:∵点A( ,2)在反比例函数 (m为常数)的图象上,
∴m= ×2=1,
∴反比例函数 (m为常数)对应的函数表达式是 .
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A( ,2),D(1,0),
∴ ,解得: ,
∴直线l对应的函数表达式为y=﹣4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣ ,﹣2).
∵CE∥x轴交直线l于点E,∴yE=yC,∴点E的坐标为E( ,﹣2).
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,
∵点B(3,n)在反比例函数图象上,
∴n= ,
∴B(3, ),G( , ),H(﹣ , ).
在Rt△ABG中,tan∠ABH= ,
在Rt△BCH中,tan∠CBH= ,
∴tan∠ABN=tan∠CBN
同课章节目录
