2024年中考数学高频考点突破——二次函数与特殊四边形(含答案)
文档属性
| 名称 | 2024年中考数学高频考点突破——二次函数与特殊四边形(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 741.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 00:00:00 | ||
图片预览



文档简介
2024年中考数学高频考点突破——
二次函数与特殊四边形
1.如图,抛物线经过点,,点是直线上的动点,过点作轴的垂线交抛物线于点.设点的横坐标为.
(1)求抛物线的解析式;
(2)若点在第一象限,连接,当线段最长时,求的面积;
(3)是否存在这样的点,使以点为顶点的四边形为平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于点,作直线,点是抛物线在第四象限上一个动点(点不与点重合),连结,,以,为边作,点的横坐标为.
(1)求抛物线对应的函数表达式;
(2)当有两个顶点在轴上时,则点的坐标为____________;
(3)当是菱形时,求的值.
(4)当为何值时,的面积有最大值?
3.如图,在平面直角坐标系中,抛物线经过,,.
(1)请写出抛物线的解析式.
(2)若点为第一象限内抛物线上的一动点,点的横坐标为,请求出使点到直线距离最大的的值.
(3)点在抛物线对称轴上,点在轴上,请写出使得以,,,为顶点的四边形是平行四边形的点的坐标.
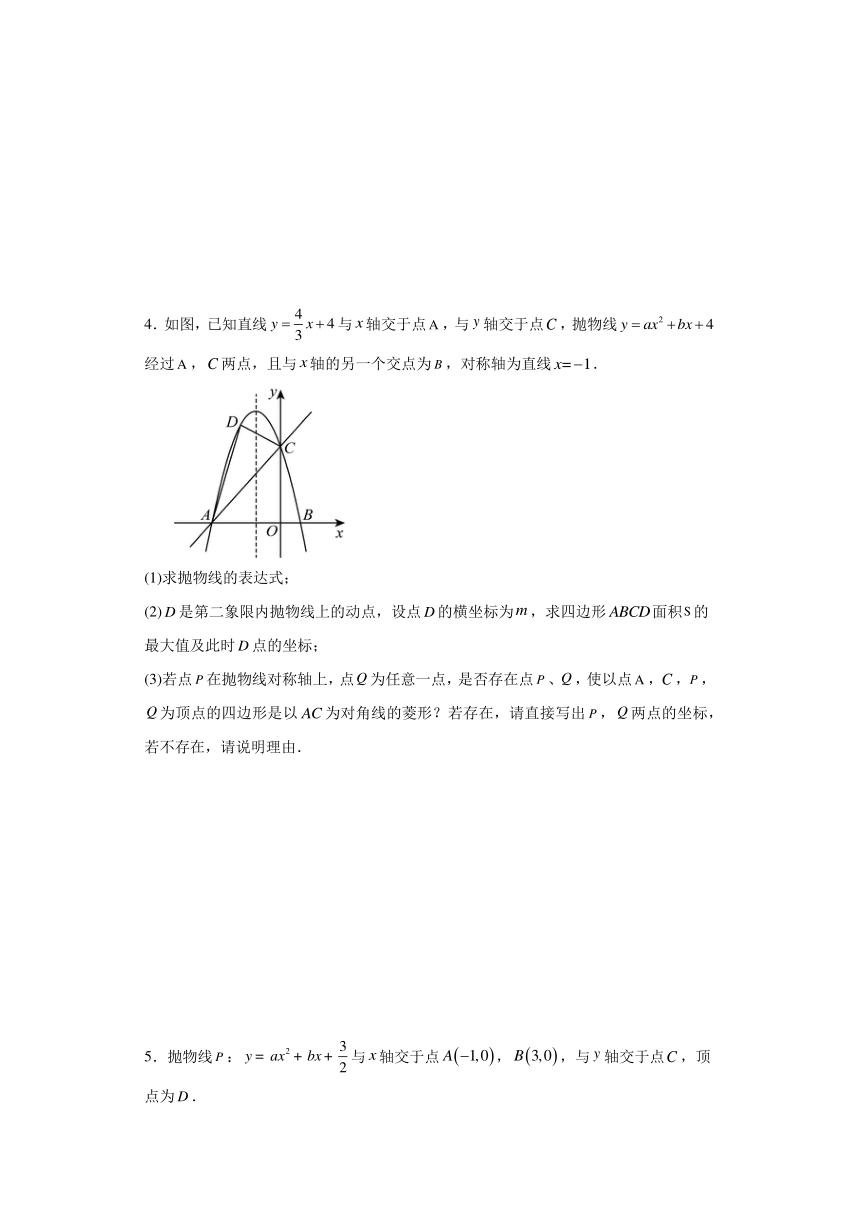
4.如图,已知直线与轴交于点,与轴交于点,抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,求四边形面积的最大值及此时点的坐标;
(3)若点在抛物线对称轴上,点为任意一点,是否存在点、,使以点,,,为顶点的四边形是以为对角线的菱形?若存在,请直接写出,两点的坐标,若不存在,请说明理由.
5.抛物线:与轴交于点,,与轴交于点,顶点为.
(1)求抛物线的解析式和顶点的坐标.
(2)如图,在坐标平面上放置一透明矩形胶片,并在胶片上描画出抛物线在矩形胶片内部(含边界)的一段,记为,把该胶片绕点顺时针旋转,得到矩形胶片以及对应的图像.
①求旋转过程中扫过的面积;
②求图像所在的抛物线的解析式.
6.如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
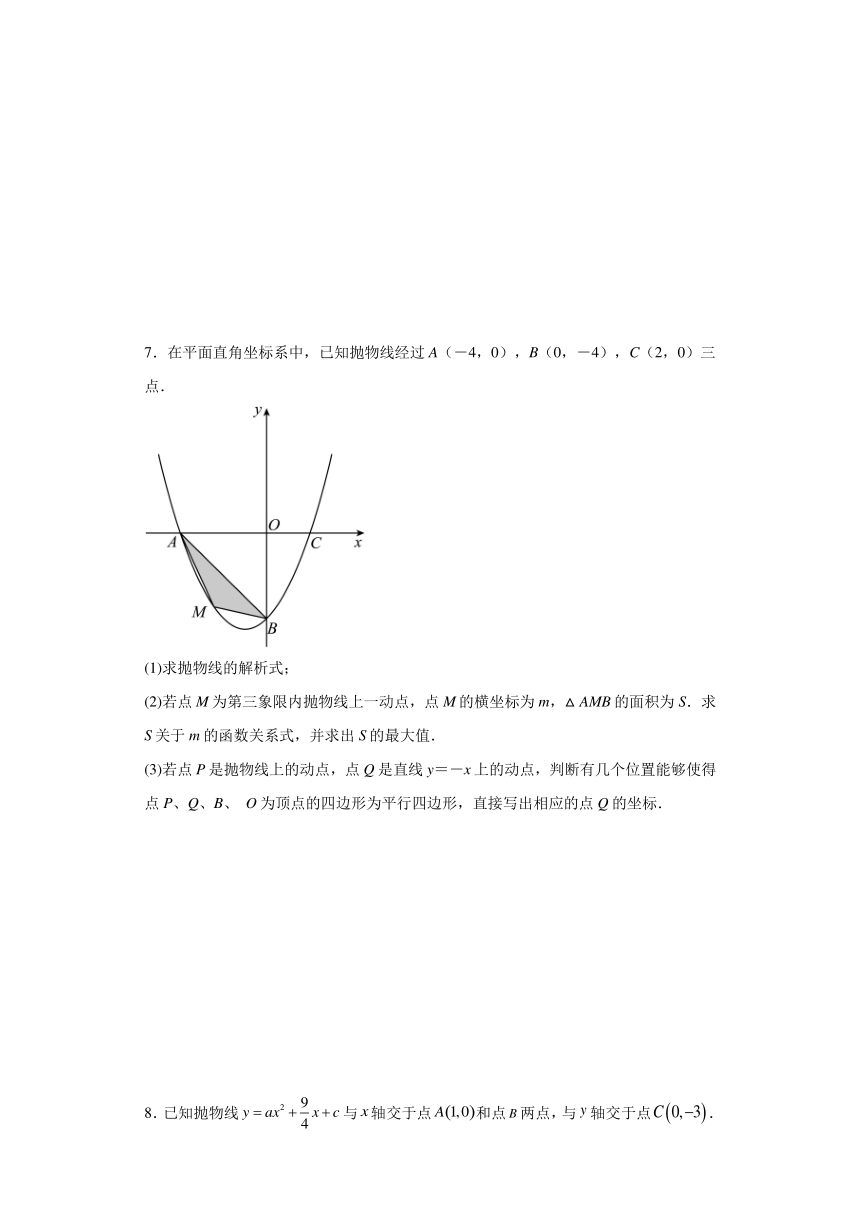
7.在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
8.已知抛物线与轴交于点和点两点,与轴交于点.
(1)求抛物线的解析式;
(2)点是抛物线上一动点(不与点,,重合),作轴,垂足为,连接.
①如图1,若点在第三象限,且,求点的坐标;
②直线交直线于点,当点关于直线的对称点落在轴上时,求四边形的周长.
9.如图,在平面直角坐标系.xOy中,直线y=x﹣4与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(﹣2,0).
(1)求抛物线解析式;
(2)如图1,点F是直线AB下方抛物线上一动点,连接FA,FB,求出四边形FAOB面积最大值及此时点F的坐标.
(3)如图2,在(2)问的条件下,点Q为平面内y轴右侧的一点,是否存在点Q及平面内任意一点M使得以A,F,Q,M为顶点的四边形是正方形?若存在,直接写出点Q的坐标;若不存在,说明理由.
10.如图,抛物线与轴交于,两点,与轴交于点,直线的解析式为.
(1)求抛物线的解析式;
(2)已知为正数,当时,的最大值和最小值分别为,,且,求的值;
(3)点是平面内任意一点,在抛物线对称轴上是否存在点,使得以点,,,为顶点的四边形是菱形?若存在,求出点的坐标;若不存在,请说明理由.
11.综合与探究
如图,抛物线与x轴交于A,B两点,与y轴交于点C.点M是y轴右侧抛物线上一动点,过点M作的平行线,交直线于点D,交x轴于点E.
(1)请直接写出点A,B,C的坐标及直线的解析式;
(2)当时,求点D的坐标;
(3)试探究在点M运动的过程中,是否存在以点A,C,E,M,为顶点的四边形是平行四边形?若存在,直接写出M的坐标,若不存在说明理由.
12.如图,抛物线y= x2+6x 5与x轴交于点A和点B,与y轴交于点C,经过B、C两点的直线为y=x 5,
(1)写出相应点的坐标:A______,B______,C______;
(2)点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大,并求出最大值.
(3)过点A作AM⊥BC于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
13.在平面直角坐标系xOy中,对于二次函数y=﹣x2+2mx-m2+4(m是常数),当m=1时,记二次函数的图象为C1;m≠1时,记二次函数的图象为C2.如图1,图象C1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C;如图2,图象C2与x轴交于D、E两点(点D在点E的左侧).
(1)请直接写出点A、B、C的坐标;
(2)当点O、D、E中恰有一点是其余两点组成线段的中点时,m= ;
(3)如图3,C2与C1交于点P,当以点A、C、D、P为顶点的四边形是平行四边形时,求m的值.
14.综合与探究
如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A( 2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.
(1)求二次函数的表达式.
(2)当点E在线段OB上运动时(不与点O,B重合),恰有线段,求此时点P的坐标.
(3)试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.
15.()已知抛物线 交轴于点 和 ,交 轴于点 ,顶点为 .
请直接写出抛物线的解析式式及点 的坐标;
如图,点 和点 关于抛物线对称轴对称,若点 是对称轴上一点,点 是坐标平面内一点,在对称轴右侧的抛物线上存在点 ,使以点 为顶点的四边形是菱形,且,请先直接写出点 的坐标,再选择一种情况说明理由.
()直线 与抛物线 交于 两点,若在 轴上存在唯一的一点 ,使,求 的值.
试卷第1页,共3页
参考答案:
1.(1)
(2)当时,最长为,此时
(3)存在点,使以点为顶点的四边形为平行四边形,坐标为或
2.(1)
(2)
(3)
(4)当时,平行四边形的面积有最大值
3.(1)该抛物线的解析式为
(2)
(3)点的坐标为或或
4.(1)
(2)的最大值为,
(3)存在;,
5.(1)抛物线的解析式为,顶点的坐标为
(2)①;②图像所在抛物线的解析式为
6.(1)
(2)(1,0)或(2,0)
7.(1)
(2),
(3)或或或
8.(1)
(2)①;②或
9.(1)
(2)当t=2时,S四边形FAOB有最大值12,此时点F的坐标为(2,﹣4)
(3)存在,点Q的坐标Q1(8,﹣2),Q2(6,﹣6),Q3(1,﹣1),Q4(5,﹣3)
10.(1)
(2)
(3)存在,或或或或
11.(1),,,
(2)点
(3)存在,点M的坐标为(3,4)或
12.(1)(1,0),(5,0),(0,-5)
(2)当t=2时,S△BEP最大为2;
(3)点N的横坐标为:4或或.
13.(1)A(-1,0),B(3,0),C(0,3)
(2)-6,0,6
(3)3
14.(1)
(2)
(3)存在,点Q的坐标为(0,2)或(0,4)或(0,-4).
15.(1)①抛物线解析式: ,顶点坐标:
②或,
(2)或或
答案第1页,共2页
二次函数与特殊四边形
1.如图,抛物线经过点,,点是直线上的动点,过点作轴的垂线交抛物线于点.设点的横坐标为.
(1)求抛物线的解析式;
(2)若点在第一象限,连接,当线段最长时,求的面积;
(3)是否存在这样的点,使以点为顶点的四边形为平行四边形?若存在,请求出点的坐标;若不存在,请说明理由.
2.如图,在平面直角坐标系中,抛物线与轴交于点,与轴交于点,作直线,点是抛物线在第四象限上一个动点(点不与点重合),连结,,以,为边作,点的横坐标为.
(1)求抛物线对应的函数表达式;
(2)当有两个顶点在轴上时,则点的坐标为____________;
(3)当是菱形时,求的值.
(4)当为何值时,的面积有最大值?
3.如图,在平面直角坐标系中,抛物线经过,,.
(1)请写出抛物线的解析式.
(2)若点为第一象限内抛物线上的一动点,点的横坐标为,请求出使点到直线距离最大的的值.
(3)点在抛物线对称轴上,点在轴上,请写出使得以,,,为顶点的四边形是平行四边形的点的坐标.
4.如图,已知直线与轴交于点,与轴交于点,抛物线经过,两点,且与轴的另一个交点为,对称轴为直线.
(1)求抛物线的表达式;
(2)是第二象限内抛物线上的动点,设点的横坐标为,求四边形面积的最大值及此时点的坐标;
(3)若点在抛物线对称轴上,点为任意一点,是否存在点、,使以点,,,为顶点的四边形是以为对角线的菱形?若存在,请直接写出,两点的坐标,若不存在,请说明理由.
5.抛物线:与轴交于点,,与轴交于点,顶点为.
(1)求抛物线的解析式和顶点的坐标.
(2)如图,在坐标平面上放置一透明矩形胶片,并在胶片上描画出抛物线在矩形胶片内部(含边界)的一段,记为,把该胶片绕点顺时针旋转,得到矩形胶片以及对应的图像.
①求旋转过程中扫过的面积;
②求图像所在的抛物线的解析式.
6.如图,抛物线y=ax2+bx+3与x轴相交于点A(﹣1,0)、B(3,0),与y轴相交于点C,点P为线段OB上的动点(不与O、B重合),过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F,点D在y轴正半轴上,OD=2,连接DE、OF.
(1)求抛物线的解析式;
(2)当四边形ODEF是平行四边形时,求点P的坐标;
7.在平面直角坐标系中,已知抛物线经过A(-4,0),B(0,-4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
(3)若点P是抛物线上的动点,点Q是直线y=-x上的动点,判断有几个位置能够使得点P、Q、B、 O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
8.已知抛物线与轴交于点和点两点,与轴交于点.
(1)求抛物线的解析式;
(2)点是抛物线上一动点(不与点,,重合),作轴,垂足为,连接.
①如图1,若点在第三象限,且,求点的坐标;
②直线交直线于点,当点关于直线的对称点落在轴上时,求四边形的周长.
9.如图,在平面直角坐标系.xOy中,直线y=x﹣4与x轴交于点A,与y轴交于点B,过A,B两点的抛物线交x轴于另一点C(﹣2,0).
(1)求抛物线解析式;
(2)如图1,点F是直线AB下方抛物线上一动点,连接FA,FB,求出四边形FAOB面积最大值及此时点F的坐标.
(3)如图2,在(2)问的条件下,点Q为平面内y轴右侧的一点,是否存在点Q及平面内任意一点M使得以A,F,Q,M为顶点的四边形是正方形?若存在,直接写出点Q的坐标;若不存在,说明理由.
10.如图,抛物线与轴交于,两点,与轴交于点,直线的解析式为.
(1)求抛物线的解析式;
(2)已知为正数,当时,的最大值和最小值分别为,,且,求的值;
(3)点是平面内任意一点,在抛物线对称轴上是否存在点,使得以点,,,为顶点的四边形是菱形?若存在,求出点的坐标;若不存在,请说明理由.
11.综合与探究
如图,抛物线与x轴交于A,B两点,与y轴交于点C.点M是y轴右侧抛物线上一动点,过点M作的平行线,交直线于点D,交x轴于点E.
(1)请直接写出点A,B,C的坐标及直线的解析式;
(2)当时,求点D的坐标;
(3)试探究在点M运动的过程中,是否存在以点A,C,E,M,为顶点的四边形是平行四边形?若存在,直接写出M的坐标,若不存在说明理由.
12.如图,抛物线y= x2+6x 5与x轴交于点A和点B,与y轴交于点C,经过B、C两点的直线为y=x 5,
(1)写出相应点的坐标:A______,B______,C______;
(2)点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大,并求出最大值.
(3)过点A作AM⊥BC于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
13.在平面直角坐标系xOy中,对于二次函数y=﹣x2+2mx-m2+4(m是常数),当m=1时,记二次函数的图象为C1;m≠1时,记二次函数的图象为C2.如图1,图象C1与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C;如图2,图象C2与x轴交于D、E两点(点D在点E的左侧).
(1)请直接写出点A、B、C的坐标;
(2)当点O、D、E中恰有一点是其余两点组成线段的中点时,m= ;
(3)如图3,C2与C1交于点P,当以点A、C、D、P为顶点的四边形是平行四边形时,求m的值.
14.综合与探究
如图,二次函数y=ax2+bx+4的图象与x轴分别交于点A( 2,0),B(4,0),点E是x轴正半轴上的一个动点,过点E作直线PE⊥x轴,交抛物线于点P,交直线BC于点F.
(1)求二次函数的表达式.
(2)当点E在线段OB上运动时(不与点O,B重合),恰有线段,求此时点P的坐标.
(3)试探究:若点Q是y轴上一点,在点E运动过程中,是否存在点Q,使得以点C,F,P,Q为顶点的四边形为菱形,若存在,直接写出点Q的坐标;若不存在,请说明理由.
15.()已知抛物线 交轴于点 和 ,交 轴于点 ,顶点为 .
请直接写出抛物线的解析式式及点 的坐标;
如图,点 和点 关于抛物线对称轴对称,若点 是对称轴上一点,点 是坐标平面内一点,在对称轴右侧的抛物线上存在点 ,使以点 为顶点的四边形是菱形,且,请先直接写出点 的坐标,再选择一种情况说明理由.
()直线 与抛物线 交于 两点,若在 轴上存在唯一的一点 ,使,求 的值.
试卷第1页,共3页
参考答案:
1.(1)
(2)当时,最长为,此时
(3)存在点,使以点为顶点的四边形为平行四边形,坐标为或
2.(1)
(2)
(3)
(4)当时,平行四边形的面积有最大值
3.(1)该抛物线的解析式为
(2)
(3)点的坐标为或或
4.(1)
(2)的最大值为,
(3)存在;,
5.(1)抛物线的解析式为,顶点的坐标为
(2)①;②图像所在抛物线的解析式为
6.(1)
(2)(1,0)或(2,0)
7.(1)
(2),
(3)或或或
8.(1)
(2)①;②或
9.(1)
(2)当t=2时,S四边形FAOB有最大值12,此时点F的坐标为(2,﹣4)
(3)存在,点Q的坐标Q1(8,﹣2),Q2(6,﹣6),Q3(1,﹣1),Q4(5,﹣3)
10.(1)
(2)
(3)存在,或或或或
11.(1),,,
(2)点
(3)存在,点M的坐标为(3,4)或
12.(1)(1,0),(5,0),(0,-5)
(2)当t=2时,S△BEP最大为2;
(3)点N的横坐标为:4或或.
13.(1)A(-1,0),B(3,0),C(0,3)
(2)-6,0,6
(3)3
14.(1)
(2)
(3)存在,点Q的坐标为(0,2)或(0,4)或(0,-4).
15.(1)①抛物线解析式: ,顶点坐标:
②或,
(2)或或
答案第1页,共2页
同课章节目录
