2023-2024学年安徽省宣城市宣城中学高二(上)月考物理试卷(12月)(含解析)
文档属性
| 名称 | 2023-2024学年安徽省宣城市宣城中学高二(上)月考物理试卷(12月)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 624.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-01-18 18:44:38 | ||
图片预览



文档简介
2023-2024学年安徽省宣城市宣城中学高二(上)月考物理试卷(12月)
一、单选题:本大题共7小题,共28分。
1.在电磁学的发展中,许多科学家做出了不可磨灭的贡献。下列说法符合史实的是( )
A. 麦克斯韦率先提出“力线”这一概念,用来描述电磁场
B. 密立根通过实验准确测得了电子的带电量
C. 库仑通过扭秤实验得出了库仑定律,并测出了静电力常量的值
D. 赫兹通过实验证实了电磁波的存在,建立了完整的电磁场理论
2.下列各图的线圈中能产生感应电流的是空间的磁场足够大( )
A. B.
C. D.
3.如图所示,在绝缘支架上的导体和导体按图中方式接触放置,原先都不带电,先让开关,均断开,现在将一个带正电小球放置在左侧,以下判断正确的是( )
A. 小球距离较近,所以左端电荷量大于右端电荷量
B. 只闭合,则左端不带电,右端带负电
C. 只闭合,则右端不带电,左端带负电
D. 只闭合,接着移走带电小球,最后将分开,带负电
4.如图所示,平行板电容器带有等量异种电荷,与静电计相连,静电计金属外壳和电容器下极板都接地。在两极板间有一固定在点的点电荷,以表示两极板间的电场强度,表示点电荷在点的电势能,表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则下列说法正确的是
( )
A. 电容器的电容减小 B. 静电计指针的偏角减小
C. 点电荷在点的电势能减小 D. 两极板间的电场强度减小
5.如图所示,直导线在磁场区域的长度为,水平置于光滑竖直导轨上,磁感应强度大小为的匀强磁场方向水平指向纸内,导线的电阻为,电源内阻为,导线质量为,与导轨框接触良好,重力加速度大小为,欲使直导线静止不动,则电源电动势为( )
A. B. C. D.
6.如图所示,矩形线框垂直磁场放置,部分处在匀强磁场中,边与磁场边界平行且到的距离为边长的四分之一,此时线框中的磁通量为,当线框绕边转过时,线框中的磁通量为
( )
A. B. C. D.
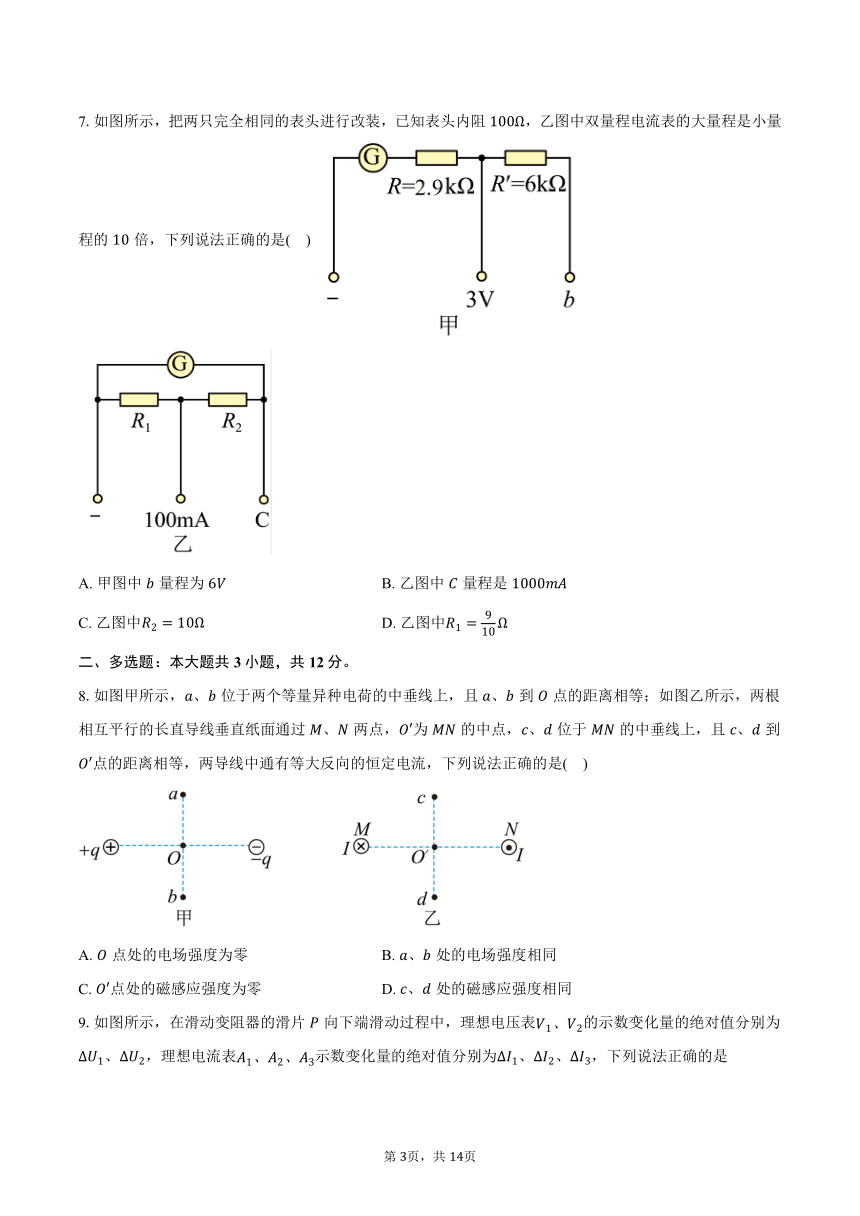
7.如图所示,把两只完全相同的表头进行改装,已知表头内阻,乙图中双量程电流表的大量程是小量程的倍,下列说法正确的是( )
A. 甲图中量程为 B. 乙图中量程是
C. 乙图中 D. 乙图中
二、多选题:本大题共3小题,共12分。
8.如图甲所示,、位于两个等量异种电荷的中垂线上,且、到点的距离相等;如图乙所示,两根相互平行的长直导线垂直纸面通过、两点,为的中点,、位于的中垂线上,且、到点的距离相等,两导线中通有等大反向的恒定电流,下列说法正确的是( )
A. 点处的电场强度为零 B. 、处的电场强度相同
C. 点处的磁感应强度为零 D. 、处的磁感应强度相同
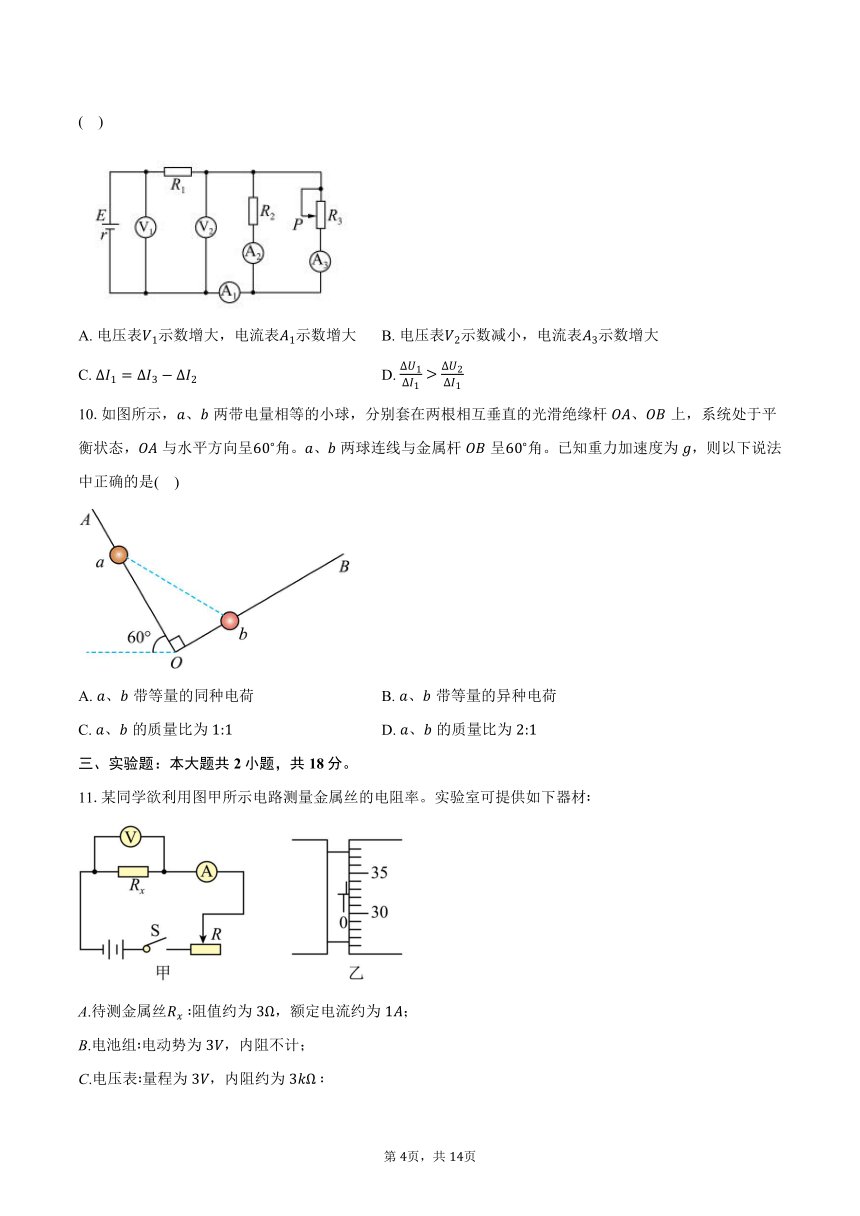
9.如图所示,在滑动变阻器的滑片向下端滑动过程中,理想电压表的示数变化量的绝对值分别为、,理想电流表示数变化量的绝对值分别为、、,下列说法正确的是
( )
A. 电压表示数增大,电流表示数增大 B. 电压表示数减小,电流表示数增大
C. D.
10.如图所示,、两带电量相等的小球,分别套在两根相互垂直的光滑绝缘杆、上,系统处于平衡状态,与水平方向呈角。、两球连线与金属杆呈角。已知重力加速度为,则以下说法中正确的是( )
A. 、带等量的同种电荷 B. 、带等量的异种电荷
C. 、的质量比为 D. 、的质量比为
三、实验题:本大题共2小题,共18分。
11.某同学欲利用图甲所示电路测量金属丝的电阻率。实验室可提供如下器材
A.待测金属丝阻值约为,额定电流约为;
B.电池组电动势为,内阻不计;
C.电压表量程为,内阻约为
D.电压表量程为,内阻约为;
E.电流表量程为,内阻约为;
F.电流表量程为,内阻约为
G.滑动变阻器调节范围为
H.螺旋测微器,毫米刻度尺,开关,导线若干。
用螺旋测微器测量金属丝的直径,示数如图乙所示,则螺旋测微器的示数为_____。
在尽可能减小测量误差的情况下,电压表应选用_____填“”或“”,电流表应选用_____填“”或“”。
若金属丝的直径为,测得长为的金属丝的两端电压为,金属丝中通过的电流为,则该金属丝的电阻率_____;从测量原理看,其测量值与真实值相比_____填“偏大”“偏小”或“相等”。
12.如图所示为某兴趣小组测量电池组的电动势和内阻的实验原理图,已知电池组的电动势约,内阻约。现提供的器材如下:
A.电池组
B.电压表量程,内阻约
C.电阻箱
D.定值电阻
E.定值电阻
F.开关和导线若干
如图所示,要尽可能精确测量电源的电动势和内阻,定值电阻应选择_________选填“”或“”。
改变电阻箱的阻值,记录对应电压表的读数,作出的图像如图所示,图线与横、纵坐标轴的截距分别为、,定值电阻的阻值用表示,则可得该电池组的电动势为_________,内阻为_________用字母、、表示。
关于这个实验中存在的误差以及减小误差的各种方法,下列说法正确的是______单选
A.电压表的分流作用引起的误差属于偶然误差
B.同学读电压表读数引起的误差属于系统误差
C.本实验用图像法处理数据可以减小偶然误差
D.如果将电压表的内阻计算在内就可以减小偶然误差
四、计算题:本大题共3小题,共30分。
13.图示固定于水平桌面上的金属框架处在竖直向下的匀强磁场中,金属棒搁在框架上,且可无摩擦滑动,此时恰好构成边长为的正方形,时磁感应强度为。求:
时穿过面的磁通量;
若从时起,磁感应强度随时间开始变化,同时棒从静止开始以加速度沿导轨方向向右匀加速运动,使棒中不产生感应电流,请推导出与的关系式。
14.如图所示,电源电动势,内阻未知,小灯泡标有“ ”,电动机的内阻。当闭合电键,将滑动变阻器的滑片调到某一合适位置时,灯泡正常发光,此时电动机的输出功率为,电流表的示数为。电表均为理想电表,求:
滑动变阻器接入电路的有效阻值;
电源的内阻。
15.边长为的立方体空间内有竖直向下的匀强电场。现有大量的同种粒子同时从立方体的中心点射向空间各个方向,其中一个沿水平面内射出的粒子恰好击中点,粒子均带正电,射出时速度的大小相等,粒子的比荷为,不计粒子重力以及粒子间的相互作用,求:
粒子射出时的初速度的大小
从点竖直向上和竖直向下射出的两粒子飞离立方体的时间间隔
若粒子从点正上方处的射出,立方体上表面有粒子到达的面积.
答案和解析
1.【答案】
【解析】A.法拉第率先提出“力线”这一概念,用来描述电磁场,选项A错误;
B.密立根通过油滴实验准确测得了电子的带电量,选项B正确;
C.库仑利用扭秤装置提出了真空中静止的点电荷间的作用规律,得出了库仑定律,麦克斯韦通过理论计算得出静电力常量的数值,故C错误;
D.麦克斯韦首先建立了完整的电磁场理论,预言了电磁波,赫兹通过实验证实了电磁波的存在,选项D错误。
故选B。
2.【答案】
【解析】【分析】
本题考查了产生感应电流的条件。
产生感应电流的条件:回路要闭合,磁通量要改变。
【解答】线圈未闭合,不能产生感应电流,故A错误;
B.穿过闭合线圈的磁通量增大,能产生感应电流,故B正确;
C.线圈与磁场平行,穿过线圈的磁通量始终为零,无变化,不能产生感应电流,故C错误;
D.穿过线圈的磁通量无变化,不能产生感应电流,故D错误。
故选B。
3.【答案】
【解析】【分析】
本题是对静电感应现象的考查,根本的原因就是电荷之间的基本性质,即同种电荷互相排斥,异种电荷互相吸引。
带电小球靠近金属导体时,由于静电感应,会使金属导体接触带电,根据静电感应的现象来分析即可。
【解答】
A.当开关,均打开时,带正电小球放置在左侧,由于静电感应,导体左端带有负电荷,右端带有正电荷,在静电平衡时,正负电荷量相等,故A错误;
B.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,左端带负电荷,故B错误;
C.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,则左端带负电,故C正确;
D.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,则左端带负电,接着移走带电小球,左端带的负电荷流向大地,将使、都不带电,故D错误。
故选C。
4.【答案】
【解析】A.由题意,若保持下极板不动,将上极板向下移动一小段距离,则根据,可知电容增大,A错误;
B.由于电容器所带电量不变,则根据,可得电容器极板间的电压减小,则静电计指针偏角减小,B正确;
根据,可得,可知电容器两极板间电场强度不变;由于电容器下极板接地,电势为零,且点离下极板的距离保持不变,根据,可知点与下极板的电势差不变,点的电势不变,根据,知 不变,CD错误。
故选B。
5.【答案】
【解析】【分析】
以直导线为研究对象,受力分析,利用直导线静止不动列平衡方程,结合闭合电路的欧姆定律求解电源电动势.
明确动力学和电学的联系纽带安培力,灵活应用平衡态和电路的知识求解,注意直导线的电阻为.
【解答】
若直导线静止不动,对直导线进行受力分析可得:
解得:
故选C。
6.【答案】
【解析】设线框的面积为,磁场的磁感应强度大小为,则
当线框转过时,线框中的磁通量
故选:。
7.【答案】
【解析】A.由甲图可知满偏电流为
其中的量程为
故A错误;
根据乙图可知接为小量程,即量程为,电流表时,并联电阻的分流电流为
分流电阻的阻值为
改装为电流表时,
联立解得,,故C正确,BD错误。
故选C。
8.【答案】
【解析】A.点处的电场强度向右,不为零,故A错误;
B.、处的电场强度向右,方向相同,大小相等,故B正确;
C.根据安培定则可知,两导线在点处的磁感应强度等大同向,则点处的磁感应强度不为零,故 C错误;
D.根据安培定则可知,、处的磁感应强度相同,方向向下,故D正确。
故选BD。
9.【答案】
【解析】【分析】
本题主要考查闭合电路欧姆定律的动态分析问题,明确电路结构是解决问题的关键。滑片向下滑动的过程中,滑动变阻器接入电路的电阻减小,总电阻变小,结合闭合欧姆定律和部分电路欧姆定律分析各电压表和电流表的示数变化;电流表的示数等于电流表的示数与电流表的示数之和,结合电流表示数的变化情况分析电流表示数变化量的绝对值之间的关系;根据闭合电路欧姆定律可知与的值,由此分析与的大小关系,即可正确求解。
【解答】
滑片向下滑动的过程中,滑动变阻器接入电路的电阻减小,电路中总电阻减小,干路电流增大,即电流表示数增大,电源内电压增大,路端电压减小,电压表示数减小,电阻分压增大,并联支路电压减小,即电压表示数减小,通过电阻的电流减小,即电流表示数减小,总电流等于通过电流表、的电流之和,所以电流表示数增大,故A错误,B正确;
C.由于电流表示数增大,示数减小,示数增大,则有,故C正确;
D.由闭合电路欧姆定律可得,,则有,故D错误。
故选BC。
10.【答案】
【解析】【分析】
本题关键是对、两带电量相等的小球进行受力分析,再利用平衡方程联立求解,、两带电量相等的小球分别静止在和两根杆上,根据平衡方程求出、的质量比。
【解答】、由受力关系可知,要保证两球平衡,、带等量的同种电荷,A正确,B错误
、如图所示,对小球进行受力分析,库仑力大小为,杆对小球的弹力大小为,设与水平方向的夹角为,与水平方向的夹角为,根据图中的几何关系有
根据物体的平衡条件有,,求得,
受力分析小球,根据如上分析,其所受库仑力的大小也为,杆对小球的弹力为,设与水平方向的夹角为,与水平方向的夹角为,根据图中的几何关系有,
根据物体的受力平衡条件有,,
求得,,故C正确,D错误。
故选AC。
11.【答案】;
;;
;偏小。
【解析】【分析】
本题考查电阻率的测量,目的是考查学生的实验能力。
螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数,注意需要估读。
根据电源电动势选择电压表,根据滑动变阻器最大阻值选择电流表;
应用欧姆定律求出金属丝的电阻表达式,然后应用电阻定律求出金属丝的电阻率,根据实验连接方式分析误差原因。
【解答】
螺旋测微器的示数为。
由于电池的电动势只有,故电压表应选用量程为的,故选C;由于滑动变阻器的最大阻值为,为减小实验误差,电流表应选用量程为的,故选E。
金属丝的横截面积,金属丝的电阻,由电阻定律有,
解得;如甲图所示,因电压表有分流作用,导致测量的电流值比真实值大,其测量值与真实值相比偏小。
12.【答案】;;;
【解析】【分析】
根据实验器材与实验目的确定实验原理,然后根据实验目的与实验所给实验器材分析答题;
应用闭合电路欧姆定律求出图象的函数表达式,然后根据图示图象求电源电动势与内阻;
根据实验误差来源分析实验误差。
本题考查测量电动势和内阻的实验,要注意明确实验原理,能根据图象法进行分析,同时利用函数规律进行分析求解即可。
【解答】
该测量电路为串联电路,根据串联分压原理可知,若定值电阻选择过大,则在调节电阻箱的过程中电压表的示数变化不明显,因此为了在调节电阻箱时增强调节的灵敏性,使电压表示数的变化更明显,则应选择阻值小的定值电阻,故选 D。
根据电路图,由闭合电路的欧姆定律可得
整理可得
结合图像可得,
解得,
电压表的分流作用引起的误差属于系统误差,A错误
B.同学读电压表读数引起的误差属于偶然误差, B错误
C.本实验用图像法处理数据可以减小偶然误差,C正确
D.如果将电压表的内阻计算在内就可以减小系统误差,D错误。
故选C。
13.【答案】根据题意,由公式 可得, 时穿过 面的磁通量为
根据题意可知,运动过程中,棒 中不产生感应电流,则穿过 面的磁通量不变,设运动时间为,则有
整理可得
【解析】解答本题时,要知道当回路中没有感应电流产生时,回路总的磁通量应保持不变。
14.【答案】灯泡正常发光,根据得:
流过灯泡的额定电流
因此流过电动机的电流
电动机产生的热功率为
电动机总功率为,其中
解得
,
联立解得;
电流表的示数为,干路中的总电流为:
闭合电路欧姆定律:
解得:。
【解析】解决本题时,要知道电动机工作时,其电路是非纯电阻电路,
灯泡正常发光,根据求出通过流过灯泡的额定电流,根据电动机总功率等于电动机产生的热功率和电动机的输出功率之和即可求解电动机两端电压,从而可求出滑动变阻器接入电路的有效阻值;
根据干路电流,再根据闭合电路欧姆定律求出电源的内阻。
15.【答案】粒子在立方体中的加速度,
水平面的粒子击中点,,
,
解得;
竖直向上射出的粒子做减速运动的距离为
,
解得,
向上粒子再次返回至点后,以向下运动,
则两粒子从底面射出的时间差
解得;
粒子从点以射出做斜抛运动,恰好到达上表面时速度为
由动能定理
速度关系
沿电场方向
粒子到上表面的水平距离
则粒子到达上表面的面积。
【解析】一个沿水平面内射出的粒子恰好击中点,该粒子做类平抛运动,根据牛顿第二定律结合运动的合成与分解规律列式求出
根据运动学公式可知竖直向上射出的粒子不能从上表面射出立方体,则向上运动的粒子从发射到再次回到点的时间即为。
根据动能定理分析粒子到达上表面的速度,根据运动的合成与分解规律求出粒子到上表面的水平距离,再由几何关系求立方体上表面有粒子到达的面积.
第1页,共1页
一、单选题:本大题共7小题,共28分。
1.在电磁学的发展中,许多科学家做出了不可磨灭的贡献。下列说法符合史实的是( )
A. 麦克斯韦率先提出“力线”这一概念,用来描述电磁场
B. 密立根通过实验准确测得了电子的带电量
C. 库仑通过扭秤实验得出了库仑定律,并测出了静电力常量的值
D. 赫兹通过实验证实了电磁波的存在,建立了完整的电磁场理论
2.下列各图的线圈中能产生感应电流的是空间的磁场足够大( )
A. B.
C. D.
3.如图所示,在绝缘支架上的导体和导体按图中方式接触放置,原先都不带电,先让开关,均断开,现在将一个带正电小球放置在左侧,以下判断正确的是( )
A. 小球距离较近,所以左端电荷量大于右端电荷量
B. 只闭合,则左端不带电,右端带负电
C. 只闭合,则右端不带电,左端带负电
D. 只闭合,接着移走带电小球,最后将分开,带负电
4.如图所示,平行板电容器带有等量异种电荷,与静电计相连,静电计金属外壳和电容器下极板都接地。在两极板间有一固定在点的点电荷,以表示两极板间的电场强度,表示点电荷在点的电势能,表示静电计指针的偏角。若保持下极板不动,将上极板向下移动一小段距离至图中虚线位置,则下列说法正确的是
( )
A. 电容器的电容减小 B. 静电计指针的偏角减小
C. 点电荷在点的电势能减小 D. 两极板间的电场强度减小
5.如图所示,直导线在磁场区域的长度为,水平置于光滑竖直导轨上,磁感应强度大小为的匀强磁场方向水平指向纸内,导线的电阻为,电源内阻为,导线质量为,与导轨框接触良好,重力加速度大小为,欲使直导线静止不动,则电源电动势为( )
A. B. C. D.
6.如图所示,矩形线框垂直磁场放置,部分处在匀强磁场中,边与磁场边界平行且到的距离为边长的四分之一,此时线框中的磁通量为,当线框绕边转过时,线框中的磁通量为
( )
A. B. C. D.
7.如图所示,把两只完全相同的表头进行改装,已知表头内阻,乙图中双量程电流表的大量程是小量程的倍,下列说法正确的是( )
A. 甲图中量程为 B. 乙图中量程是
C. 乙图中 D. 乙图中
二、多选题:本大题共3小题,共12分。
8.如图甲所示,、位于两个等量异种电荷的中垂线上,且、到点的距离相等;如图乙所示,两根相互平行的长直导线垂直纸面通过、两点,为的中点,、位于的中垂线上,且、到点的距离相等,两导线中通有等大反向的恒定电流,下列说法正确的是( )
A. 点处的电场强度为零 B. 、处的电场强度相同
C. 点处的磁感应强度为零 D. 、处的磁感应强度相同
9.如图所示,在滑动变阻器的滑片向下端滑动过程中,理想电压表的示数变化量的绝对值分别为、,理想电流表示数变化量的绝对值分别为、、,下列说法正确的是
( )
A. 电压表示数增大,电流表示数增大 B. 电压表示数减小,电流表示数增大
C. D.
10.如图所示,、两带电量相等的小球,分别套在两根相互垂直的光滑绝缘杆、上,系统处于平衡状态,与水平方向呈角。、两球连线与金属杆呈角。已知重力加速度为,则以下说法中正确的是( )
A. 、带等量的同种电荷 B. 、带等量的异种电荷
C. 、的质量比为 D. 、的质量比为
三、实验题:本大题共2小题,共18分。
11.某同学欲利用图甲所示电路测量金属丝的电阻率。实验室可提供如下器材
A.待测金属丝阻值约为,额定电流约为;
B.电池组电动势为,内阻不计;
C.电压表量程为,内阻约为
D.电压表量程为,内阻约为;
E.电流表量程为,内阻约为;
F.电流表量程为,内阻约为
G.滑动变阻器调节范围为
H.螺旋测微器,毫米刻度尺,开关,导线若干。
用螺旋测微器测量金属丝的直径,示数如图乙所示,则螺旋测微器的示数为_____。
在尽可能减小测量误差的情况下,电压表应选用_____填“”或“”,电流表应选用_____填“”或“”。
若金属丝的直径为,测得长为的金属丝的两端电压为,金属丝中通过的电流为,则该金属丝的电阻率_____;从测量原理看,其测量值与真实值相比_____填“偏大”“偏小”或“相等”。
12.如图所示为某兴趣小组测量电池组的电动势和内阻的实验原理图,已知电池组的电动势约,内阻约。现提供的器材如下:
A.电池组
B.电压表量程,内阻约
C.电阻箱
D.定值电阻
E.定值电阻
F.开关和导线若干
如图所示,要尽可能精确测量电源的电动势和内阻,定值电阻应选择_________选填“”或“”。
改变电阻箱的阻值,记录对应电压表的读数,作出的图像如图所示,图线与横、纵坐标轴的截距分别为、,定值电阻的阻值用表示,则可得该电池组的电动势为_________,内阻为_________用字母、、表示。
关于这个实验中存在的误差以及减小误差的各种方法,下列说法正确的是______单选
A.电压表的分流作用引起的误差属于偶然误差
B.同学读电压表读数引起的误差属于系统误差
C.本实验用图像法处理数据可以减小偶然误差
D.如果将电压表的内阻计算在内就可以减小偶然误差
四、计算题:本大题共3小题,共30分。
13.图示固定于水平桌面上的金属框架处在竖直向下的匀强磁场中,金属棒搁在框架上,且可无摩擦滑动,此时恰好构成边长为的正方形,时磁感应强度为。求:
时穿过面的磁通量;
若从时起,磁感应强度随时间开始变化,同时棒从静止开始以加速度沿导轨方向向右匀加速运动,使棒中不产生感应电流,请推导出与的关系式。
14.如图所示,电源电动势,内阻未知,小灯泡标有“ ”,电动机的内阻。当闭合电键,将滑动变阻器的滑片调到某一合适位置时,灯泡正常发光,此时电动机的输出功率为,电流表的示数为。电表均为理想电表,求:
滑动变阻器接入电路的有效阻值;
电源的内阻。
15.边长为的立方体空间内有竖直向下的匀强电场。现有大量的同种粒子同时从立方体的中心点射向空间各个方向,其中一个沿水平面内射出的粒子恰好击中点,粒子均带正电,射出时速度的大小相等,粒子的比荷为,不计粒子重力以及粒子间的相互作用,求:
粒子射出时的初速度的大小
从点竖直向上和竖直向下射出的两粒子飞离立方体的时间间隔
若粒子从点正上方处的射出,立方体上表面有粒子到达的面积.
答案和解析
1.【答案】
【解析】A.法拉第率先提出“力线”这一概念,用来描述电磁场,选项A错误;
B.密立根通过油滴实验准确测得了电子的带电量,选项B正确;
C.库仑利用扭秤装置提出了真空中静止的点电荷间的作用规律,得出了库仑定律,麦克斯韦通过理论计算得出静电力常量的数值,故C错误;
D.麦克斯韦首先建立了完整的电磁场理论,预言了电磁波,赫兹通过实验证实了电磁波的存在,选项D错误。
故选B。
2.【答案】
【解析】【分析】
本题考查了产生感应电流的条件。
产生感应电流的条件:回路要闭合,磁通量要改变。
【解答】线圈未闭合,不能产生感应电流,故A错误;
B.穿过闭合线圈的磁通量增大,能产生感应电流,故B正确;
C.线圈与磁场平行,穿过线圈的磁通量始终为零,无变化,不能产生感应电流,故C错误;
D.穿过线圈的磁通量无变化,不能产生感应电流,故D错误。
故选B。
3.【答案】
【解析】【分析】
本题是对静电感应现象的考查,根本的原因就是电荷之间的基本性质,即同种电荷互相排斥,异种电荷互相吸引。
带电小球靠近金属导体时,由于静电感应,会使金属导体接触带电,根据静电感应的现象来分析即可。
【解答】
A.当开关,均打开时,带正电小球放置在左侧,由于静电感应,导体左端带有负电荷,右端带有正电荷,在静电平衡时,正负电荷量相等,故A错误;
B.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,左端带负电荷,故B错误;
C.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,则左端带负电,故C正确;
D.只闭合,则右端带的正电荷与大地的负电荷中和,而不带电,由于静电感应,则左端带负电,接着移走带电小球,左端带的负电荷流向大地,将使、都不带电,故D错误。
故选C。
4.【答案】
【解析】A.由题意,若保持下极板不动,将上极板向下移动一小段距离,则根据,可知电容增大,A错误;
B.由于电容器所带电量不变,则根据,可得电容器极板间的电压减小,则静电计指针偏角减小,B正确;
根据,可得,可知电容器两极板间电场强度不变;由于电容器下极板接地,电势为零,且点离下极板的距离保持不变,根据,可知点与下极板的电势差不变,点的电势不变,根据,知 不变,CD错误。
故选B。
5.【答案】
【解析】【分析】
以直导线为研究对象,受力分析,利用直导线静止不动列平衡方程,结合闭合电路的欧姆定律求解电源电动势.
明确动力学和电学的联系纽带安培力,灵活应用平衡态和电路的知识求解,注意直导线的电阻为.
【解答】
若直导线静止不动,对直导线进行受力分析可得:
解得:
故选C。
6.【答案】
【解析】设线框的面积为,磁场的磁感应强度大小为,则
当线框转过时,线框中的磁通量
故选:。
7.【答案】
【解析】A.由甲图可知满偏电流为
其中的量程为
故A错误;
根据乙图可知接为小量程,即量程为,电流表时,并联电阻的分流电流为
分流电阻的阻值为
改装为电流表时,
联立解得,,故C正确,BD错误。
故选C。
8.【答案】
【解析】A.点处的电场强度向右,不为零,故A错误;
B.、处的电场强度向右,方向相同,大小相等,故B正确;
C.根据安培定则可知,两导线在点处的磁感应强度等大同向,则点处的磁感应强度不为零,故 C错误;
D.根据安培定则可知,、处的磁感应强度相同,方向向下,故D正确。
故选BD。
9.【答案】
【解析】【分析】
本题主要考查闭合电路欧姆定律的动态分析问题,明确电路结构是解决问题的关键。滑片向下滑动的过程中,滑动变阻器接入电路的电阻减小,总电阻变小,结合闭合欧姆定律和部分电路欧姆定律分析各电压表和电流表的示数变化;电流表的示数等于电流表的示数与电流表的示数之和,结合电流表示数的变化情况分析电流表示数变化量的绝对值之间的关系;根据闭合电路欧姆定律可知与的值,由此分析与的大小关系,即可正确求解。
【解答】
滑片向下滑动的过程中,滑动变阻器接入电路的电阻减小,电路中总电阻减小,干路电流增大,即电流表示数增大,电源内电压增大,路端电压减小,电压表示数减小,电阻分压增大,并联支路电压减小,即电压表示数减小,通过电阻的电流减小,即电流表示数减小,总电流等于通过电流表、的电流之和,所以电流表示数增大,故A错误,B正确;
C.由于电流表示数增大,示数减小,示数增大,则有,故C正确;
D.由闭合电路欧姆定律可得,,则有,故D错误。
故选BC。
10.【答案】
【解析】【分析】
本题关键是对、两带电量相等的小球进行受力分析,再利用平衡方程联立求解,、两带电量相等的小球分别静止在和两根杆上,根据平衡方程求出、的质量比。
【解答】、由受力关系可知,要保证两球平衡,、带等量的同种电荷,A正确,B错误
、如图所示,对小球进行受力分析,库仑力大小为,杆对小球的弹力大小为,设与水平方向的夹角为,与水平方向的夹角为,根据图中的几何关系有
根据物体的平衡条件有,,求得,
受力分析小球,根据如上分析,其所受库仑力的大小也为,杆对小球的弹力为,设与水平方向的夹角为,与水平方向的夹角为,根据图中的几何关系有,
根据物体的受力平衡条件有,,
求得,,故C正确,D错误。
故选AC。
11.【答案】;
;;
;偏小。
【解析】【分析】
本题考查电阻率的测量,目的是考查学生的实验能力。
螺旋测微器固定刻度与可动刻度示数之和是螺旋测微器的示数,注意需要估读。
根据电源电动势选择电压表,根据滑动变阻器最大阻值选择电流表;
应用欧姆定律求出金属丝的电阻表达式,然后应用电阻定律求出金属丝的电阻率,根据实验连接方式分析误差原因。
【解答】
螺旋测微器的示数为。
由于电池的电动势只有,故电压表应选用量程为的,故选C;由于滑动变阻器的最大阻值为,为减小实验误差,电流表应选用量程为的,故选E。
金属丝的横截面积,金属丝的电阻,由电阻定律有,
解得;如甲图所示,因电压表有分流作用,导致测量的电流值比真实值大,其测量值与真实值相比偏小。
12.【答案】;;;
【解析】【分析】
根据实验器材与实验目的确定实验原理,然后根据实验目的与实验所给实验器材分析答题;
应用闭合电路欧姆定律求出图象的函数表达式,然后根据图示图象求电源电动势与内阻;
根据实验误差来源分析实验误差。
本题考查测量电动势和内阻的实验,要注意明确实验原理,能根据图象法进行分析,同时利用函数规律进行分析求解即可。
【解答】
该测量电路为串联电路,根据串联分压原理可知,若定值电阻选择过大,则在调节电阻箱的过程中电压表的示数变化不明显,因此为了在调节电阻箱时增强调节的灵敏性,使电压表示数的变化更明显,则应选择阻值小的定值电阻,故选 D。
根据电路图,由闭合电路的欧姆定律可得
整理可得
结合图像可得,
解得,
电压表的分流作用引起的误差属于系统误差,A错误
B.同学读电压表读数引起的误差属于偶然误差, B错误
C.本实验用图像法处理数据可以减小偶然误差,C正确
D.如果将电压表的内阻计算在内就可以减小系统误差,D错误。
故选C。
13.【答案】根据题意,由公式 可得, 时穿过 面的磁通量为
根据题意可知,运动过程中,棒 中不产生感应电流,则穿过 面的磁通量不变,设运动时间为,则有
整理可得
【解析】解答本题时,要知道当回路中没有感应电流产生时,回路总的磁通量应保持不变。
14.【答案】灯泡正常发光,根据得:
流过灯泡的额定电流
因此流过电动机的电流
电动机产生的热功率为
电动机总功率为,其中
解得
,
联立解得;
电流表的示数为,干路中的总电流为:
闭合电路欧姆定律:
解得:。
【解析】解决本题时,要知道电动机工作时,其电路是非纯电阻电路,
灯泡正常发光,根据求出通过流过灯泡的额定电流,根据电动机总功率等于电动机产生的热功率和电动机的输出功率之和即可求解电动机两端电压,从而可求出滑动变阻器接入电路的有效阻值;
根据干路电流,再根据闭合电路欧姆定律求出电源的内阻。
15.【答案】粒子在立方体中的加速度,
水平面的粒子击中点,,
,
解得;
竖直向上射出的粒子做减速运动的距离为
,
解得,
向上粒子再次返回至点后,以向下运动,
则两粒子从底面射出的时间差
解得;
粒子从点以射出做斜抛运动,恰好到达上表面时速度为
由动能定理
速度关系
沿电场方向
粒子到上表面的水平距离
则粒子到达上表面的面积。
【解析】一个沿水平面内射出的粒子恰好击中点,该粒子做类平抛运动,根据牛顿第二定律结合运动的合成与分解规律列式求出
根据运动学公式可知竖直向上射出的粒子不能从上表面射出立方体,则向上运动的粒子从发射到再次回到点的时间即为。
根据动能定理分析粒子到达上表面的速度,根据运动的合成与分解规律求出粒子到上表面的水平距离,再由几何关系求立方体上表面有粒子到达的面积.
第1页,共1页
同课章节目录
