08学年高一第一学期期末复习测试卷之二

08学年高一第一学期期末复习测试卷之二
081223
一、选择题：（每小题5分，共50分）
1、下列计算中正确的是（ ）
A、 B、 C、 D、
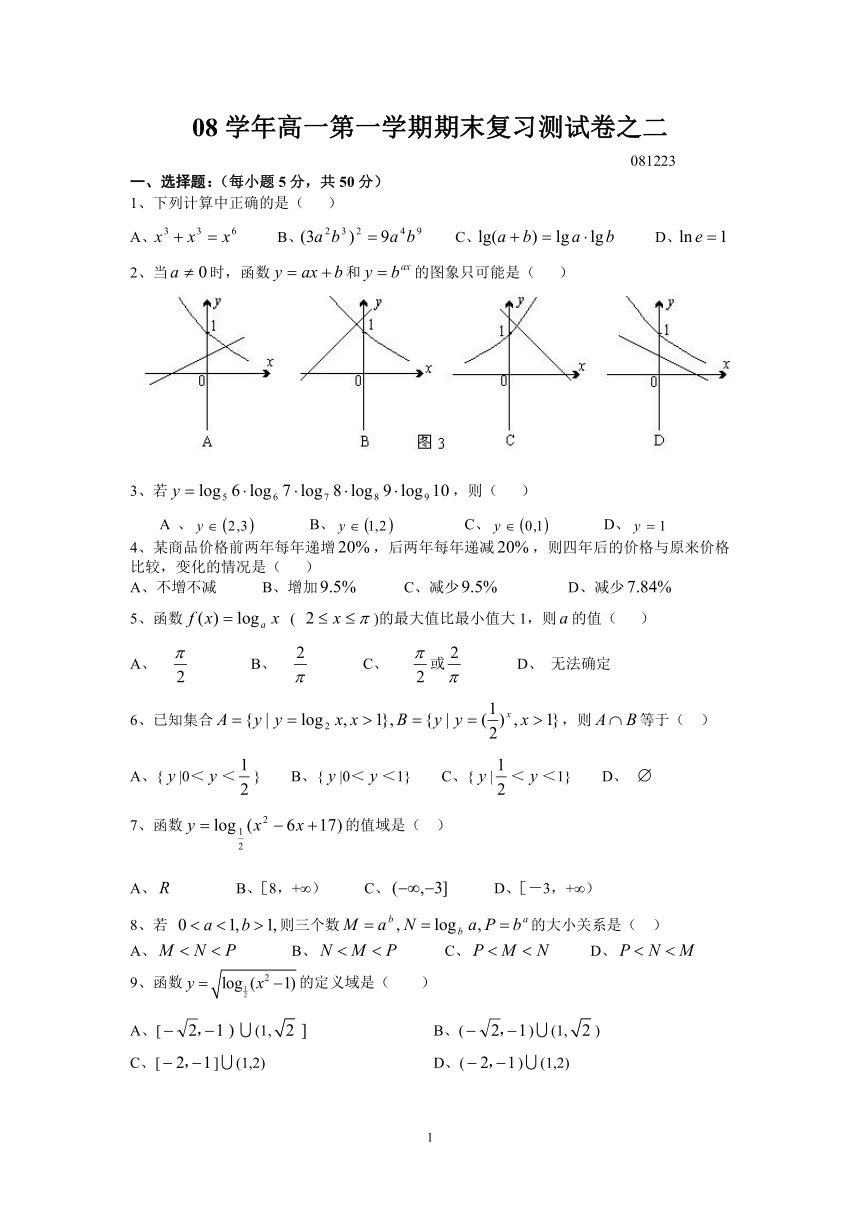
2、当时，函数和的图象只可能是（ ）
3、若，则（ ）
A 、 B、 C、 D、
4、某商品价格前两年每年递增，后两年每年递减，则四年后的价格与原来价格比较，变化的情况是（ ）
A、不增不减 B、增加 C、减少 D、减少
5、函数 ( )的最大值比最小值大1，则的值（ ）
A、 B、 C、 或 D、 无法确定
6、已知集合，则等于（ ）
A、{|0＜＜} B、{|0＜＜1} C、{|＜＜1} D、
7、函数的值域是（ ）
A、 B、［8，+∞） C、 D、［－3，+∞）
8、若 则三个数的大小关系是（ ）
A、 B、 C、 D、
9、函数的定义域是（ ）
A、[(1, B、()(1,)
C、[](1,2) D、()(1,2)
10、对于幂函数，若，则，大小关系是（ ）
A、 B、
C、 D、无法确定
二、填空题：（共7小题，共28分）
11、若集合, 则等于 __________；
12、函数= 的单调递增区间是 ；
13、已知，则三个数由小到大的顺序是 ；
14、______________；
15、函数()()的值域是 ；
16、已知，则________________；
17、方程的解为 。
三、解答题：（共5小题，共72分）
18、计算：（1）；
（2）。
19、已知函数,(1)求的定义域；(2)求的单调区间并指出其单调性；(3)求的最大值,并求取得最大值时的的值。
20、某自来水厂的蓄水池中有400吨水,每天零点开始向居民供水,同时以每小时60吨的速度向池中注水,小时内向居民供水总量为.
(1)每天几点钟时,蓄水池中的存水量最少?
(2)如果池中存水量不多于80吨,就会出现供水紧张现象,那么一天中会有几小时出现这种现象?
21、已知函数 。(1) 求函数的值域；(2) 判断并证明函数的单调性。
22、已知函数。
（1）若的定义域是，求实数的取值范围及的值域；
（2）若的值域是，求实数的取值范围及的定义域。
测试卷之二参考答案：
一、选择题：1---10 DABDC ACBAB
二、填空题：11、；12、；13、 ；14、；15、；16、2 ；17、0
三、解答题：
18、解析：（1）=5
（2）
19、解析：(1)∵2x+3-x2>0
∴-1∴函数f(x)的定义域为(-1,3) (1分)
(2)函数f(x)在(-1,1)上单调递增, (2分)
函数f(x)在(1,3)上单调递减. (2分)
(3) ∵当x=1时,2x+3-x2有最大值4 (1分)
∴当x=1时,函数f(x)取得最大值1 (1分)
20、解析：(1)设t小时后,蓄水池中的存水量为y吨.
则
设,则,
∴ 当时,y取得最小值40.
∴ 每天在6点钟时,蓄水池中的存水量最少. (5分)
(2) 由题意得:y≤80时,就会出现供水紧张.
∴
解之得
∴ ∴
∴ 一天中会有8小时出现这种供水紧张的现象.
21、解析：（1）, 又 ，
函数的值域为
（2）函数在上为单调增函数
证明：=
在定义域中任取两个实数,且

，从而
所以函数在上为单调增函数。
21、（备用）已知函数。
(1)判断函数的奇偶性和单调性；
(2)对于函数，当时，有，求实数的集合。
解析：（1）定义域为；又，所以是奇函数；单调性证明用定义，是增函数。（略）
(2)∵f(1－t)＋f(1－t2)＜0，f(x)是奇函数，且在R上为增函数，
22、解析：（1）因为f(x)的定义域为R，所以ax2+2x+1>0对一切xR成立．
由此得解得a>1. 又因为ax2+2x+1=a(x+)+1－>0，
所以f(x)=lg(a x2+2x+1) lg(1－)，所以实数a的取值范围是(1,+ ) ,
f(x)的值域是
( 2 ) 因为f(x)的值域是R，所以u=ax2+2x+1的值域(0, +).
当a=0时，u=2x+1的值域为R(0, +)；
当a≠0时，u=ax2+2x+1的值域(0, +)等价于
解之得00得x>－,
f (x)的定义域是(－,+)； 当00
解得
f (x)的定义域是.