26.1.2 反比例函数的图象和性质人教版教案设计
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质人教版教案设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 314.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 23:59:00 | ||
图片预览



文档简介
《反比例函数的图象与性质》教学设计
课 题 《反比例函数的图象与性质》
课时安排 1课时 课前准备 三角板、网格纸
教材内容 分 析 反比例函数的图象和性质是反比例函数的教学重点,学生需要在理解的基础上熟练运用。本节课是全章的核心,学习的主要内容是画反比例函数的图象,让学生结合实例,通过列表、描点、连线等手段经历画图、观察、猜想、思考、归纳等数学活动,并初步认识反比例函数的图象的特征,逐步明确反比例函数的直观形象,为学生探索反比例函数的图象的性质提供思维活动的空间。
设计理念 在新课程标准下,倡导学生主动参与、乐于探究、勤于动手,培养学生获取新知识的能力,分析和解决问题的能力以及合作交流的能力.本节课的主要内容是画反比例函数的图象,通过观察反比例函数的图象归纳反比例函数的性质:学生已经学习了利用列表、描点、连线的方法画函数图象,并且在前面学习了正比例函数,一次函数,二次函数,学生也知道了研究函数的一般方法.针对于本节课的内容以及学生的实际情况,让学生动手操作,自主学习完成本节课的内容,更好地培养学生的自学能力和小组合作学习意识.
学情分析 知识方面,九年级的学生对函数并不陌生,在八年级下学期学习了正比例函数,一次函数,在九年级上学期学习了二次函数,对于函数知识有了一定的认识.方法上,对新知识的学习采用画图、观察、类比、归纳等方法,根据研究函数的一般方法来探究反比例函数的性质.心理上,九年级学生的学龄特点是知识有了一定的积淀,积极主动,并勇于大胆猜想,积极探索;技能上,学生已经学会用列表、描点、连线来画函数的图象;以上各方面的准备,都为本次完成学习任务奠定的基础.
教学目标 (1)会根据解析式画反比例函数的图象,归纳得到反比例函数的图象特征和性质。 (2)在画出反比例函数的图象,并探究其性质的过程中,体会“分类讨论”“数形结合”以及“从特殊到一般”的数学思想。
教学重难点 教学重点:由反比例函数的图象,并结合解析式,探究反比例函数的性质。 难点:对x≠0的理解,以及在x=0这点没有定义。
教学过程
教学环节(一) 师生活动 回顾与思考 1.什么是反比例函数? 2.反比例函数的定义中需要注意什么? 3.一次函数y=kx+b(k≠0)的图象是 ,二次函数的图象是 ,反比例函数的图象是什么样的呢?
设计意图 回顾反比例函数的概念、一次函数、二次函数图象及作法,为学习反比例函数的图像和性质做准备。
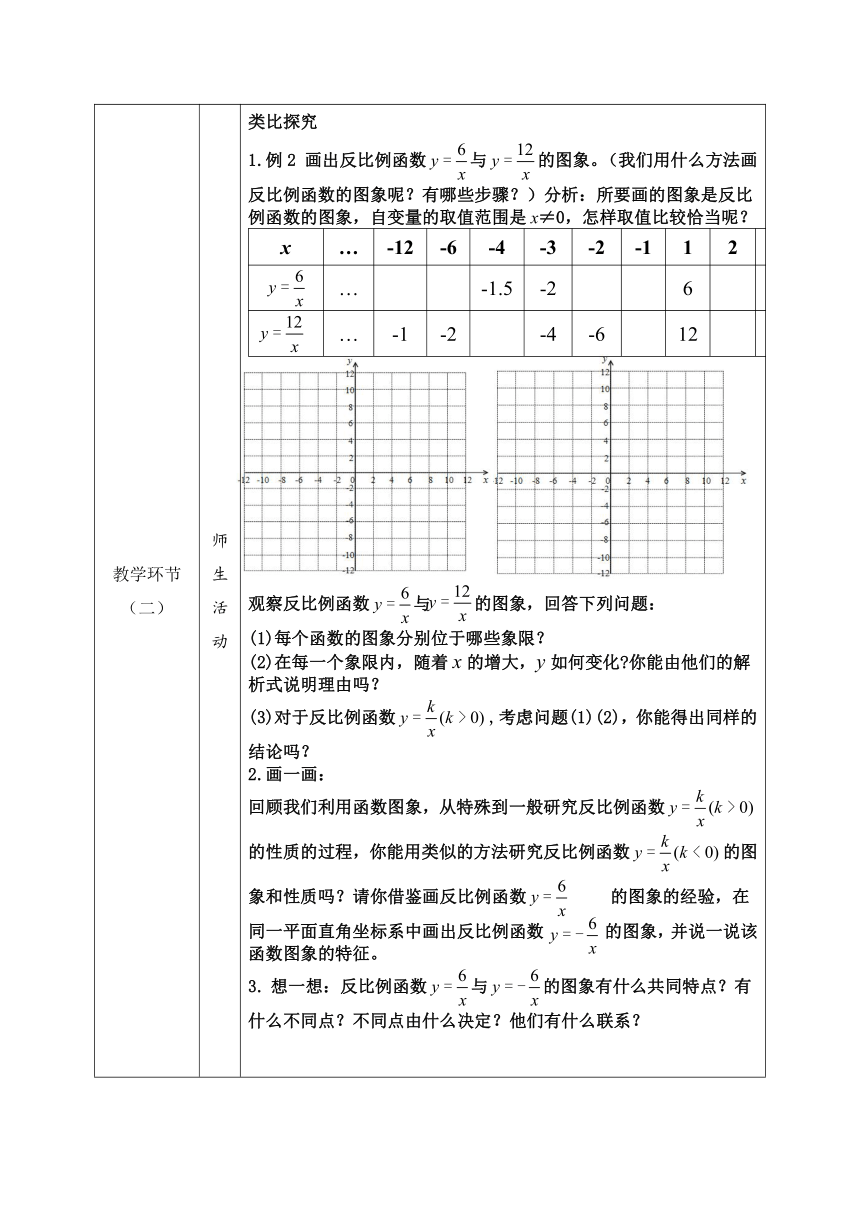
教学环节(二) 师生活动 类比探究 1.例2 画出反比例函数与的图象。(我们用什么方法画反比例函数的图象呢?有哪些步骤?)分析:所要画的图象是反比例函数的图象,自变量的取值范围是x≠0,怎样取值比较恰当呢? x…-12-6-4-3-2-11234612……-1.5-2621……-1-2-4-612431…
观察反比例函数与 的图象,回答下列问题: (1)每个函数的图象分别位于哪些象限? (2)在每一个象限内,随着x的增大,y如何变化 你能由他们的解析式说明理由吗? (3)对于反比例函数,考虑问题(1)(2),你能得出同样的结论吗? 2.画一画: 回顾我们利用函数图象,从特殊到一般研究反比例函数的性质的过程,你能用类似的方法研究反比例函数的图象和性质吗?请你借鉴画反比例函数 的图象的经验,在同一平面直角坐标系中画出反比例函数 的图象,并说一说该函数图象的特征。 想一想:反比例函数与的图象有什么共同特点?有什么不同点?不同点由什么决定?他们有什么联系?
设计意图 让学生亲自动手操作,会画反比例函数的图像,可以培养学生的动手能力,激发学生学好数学的兴趣,去为发现反比例函数的性质做准备。分组画图的目的是为后面的合作交流做铺垫。采用彩色笔,通过颜色变化,有利于反映和发现问题。
教学环节 (三) 师生活动 归纳与小结:反比例函数的图象和性质: 函数图象形状( )图象位置图象变化趋势
设计意图 通过学生自由讨论、总结、概括本节所学习的内容,使学生进一步了解反比例函数的图象及其性质,让他们体验到学习数学的快乐,在交流中与全班同学分享。
教学环节 (四) 师生活动 基础闯关 1.反比例函数的图象大致是( ) 2.已知反比例函数 若函数的图象位于第一三象限,则k_____________; 若在每一象限内,y随x增大而增大,请写出一个符合条件的k的值: 画出函数的图象: x…-8-5-4-2-112458…y……
(1)列表(填空): (2)描点连线: (3)由图象可知,函数也由 条曲线组成,分别位于第 象限,试猜想:的图象位于第 象限.
设计意图 检验学生对本课知识的掌握及应用情况。通过练习,既培养学生思维的敏捷性,又激发学生的参与和竞争意识.在回答过程中,教师给予适当评讲,并积极调动学生的参与热情,让整个课堂充满活跃的气氛.
教学环节 (五) 师生活动 中考链接 1.已知k<0,则函数在同一坐标系中的图象大致是( ) 思考:把条件“k<0”改为“k≠0”结果还是一样吗? 2.已知反比例函数的图象在第二、四象限,那么一次函数y=kx-k的图象经过( ) A.第一、二、三象限 B.第一、二、四象限 C.第一、三、四象限 D.第二、三、四象限 3.函数与在同一平面直角坐标系中的图象可能是( ) 4.(2017江西)如图,直线与双曲线相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将沿OP方向平移,使点O移动到点P,得到 .过点A'作轴交双曲线于点C。 (1)求k1与k2的值。 (2)求直线PC的表达式。 (3)直接写出线段AB扫过的面积。
设计意图 链接中考,让学生巩固本节知识的同时,综合运用反比例、一次函数、二次函数、图形的变换等知识,提前接触中考题,感受中考题来源于平时练习,可帮助考生掌握中考题目类型及部分考点,研究中考试题的解题方法和技巧,总结中考题的做题思路。
板书设计 26.1.2 反比例函数的图象和性质 1. xy=k y=kx-1 2.与 (k>0) x…-12-6-4-3-2-11234612……-0.5-1-1.5-2-3-66321.510.5……-1-2-3-4-6-121264321…
3.性质:(1)①轴对称图形,对称轴是直线y=x与y=-x。②中心对称图形。 函数图象形状( )图象位置图象变化趋势
③与关于x轴和y轴对称。④双曲线无限接近x轴和y轴,但不与其相交。 (2) 4.思想与方法:数形结合、分类讨论、从特殊到一般、类比。
教学反思 1、同桌互动画图象,改变传统的被动接受知识的教学方式,鼓励学生自己探索、合作交流。对于我班部分个别学生来说画图技巧较弱,课后需再加强辅导。 2、由于本节课的内容与正比例函数有着密切联系,学生能在旧知识中寻找模型,而最后的运用新知、拓展训练中的中考题,提升了一定的高度,有一小部分同学不那么容易理解,需要进行适当的点拨。
课 题 《反比例函数的图象与性质》
课时安排 1课时 课前准备 三角板、网格纸
教材内容 分 析 反比例函数的图象和性质是反比例函数的教学重点,学生需要在理解的基础上熟练运用。本节课是全章的核心,学习的主要内容是画反比例函数的图象,让学生结合实例,通过列表、描点、连线等手段经历画图、观察、猜想、思考、归纳等数学活动,并初步认识反比例函数的图象的特征,逐步明确反比例函数的直观形象,为学生探索反比例函数的图象的性质提供思维活动的空间。
设计理念 在新课程标准下,倡导学生主动参与、乐于探究、勤于动手,培养学生获取新知识的能力,分析和解决问题的能力以及合作交流的能力.本节课的主要内容是画反比例函数的图象,通过观察反比例函数的图象归纳反比例函数的性质:学生已经学习了利用列表、描点、连线的方法画函数图象,并且在前面学习了正比例函数,一次函数,二次函数,学生也知道了研究函数的一般方法.针对于本节课的内容以及学生的实际情况,让学生动手操作,自主学习完成本节课的内容,更好地培养学生的自学能力和小组合作学习意识.
学情分析 知识方面,九年级的学生对函数并不陌生,在八年级下学期学习了正比例函数,一次函数,在九年级上学期学习了二次函数,对于函数知识有了一定的认识.方法上,对新知识的学习采用画图、观察、类比、归纳等方法,根据研究函数的一般方法来探究反比例函数的性质.心理上,九年级学生的学龄特点是知识有了一定的积淀,积极主动,并勇于大胆猜想,积极探索;技能上,学生已经学会用列表、描点、连线来画函数的图象;以上各方面的准备,都为本次完成学习任务奠定的基础.
教学目标 (1)会根据解析式画反比例函数的图象,归纳得到反比例函数的图象特征和性质。 (2)在画出反比例函数的图象,并探究其性质的过程中,体会“分类讨论”“数形结合”以及“从特殊到一般”的数学思想。
教学重难点 教学重点:由反比例函数的图象,并结合解析式,探究反比例函数的性质。 难点:对x≠0的理解,以及在x=0这点没有定义。
教学过程
教学环节(一) 师生活动 回顾与思考 1.什么是反比例函数? 2.反比例函数的定义中需要注意什么? 3.一次函数y=kx+b(k≠0)的图象是 ,二次函数的图象是 ,反比例函数的图象是什么样的呢?
设计意图 回顾反比例函数的概念、一次函数、二次函数图象及作法,为学习反比例函数的图像和性质做准备。
教学环节(二) 师生活动 类比探究 1.例2 画出反比例函数与的图象。(我们用什么方法画反比例函数的图象呢?有哪些步骤?)分析:所要画的图象是反比例函数的图象,自变量的取值范围是x≠0,怎样取值比较恰当呢? x…-12-6-4-3-2-11234612……-1.5-2621……-1-2-4-612431…
观察反比例函数与 的图象,回答下列问题: (1)每个函数的图象分别位于哪些象限? (2)在每一个象限内,随着x的增大,y如何变化 你能由他们的解析式说明理由吗? (3)对于反比例函数,考虑问题(1)(2),你能得出同样的结论吗? 2.画一画: 回顾我们利用函数图象,从特殊到一般研究反比例函数的性质的过程,你能用类似的方法研究反比例函数的图象和性质吗?请你借鉴画反比例函数 的图象的经验,在同一平面直角坐标系中画出反比例函数 的图象,并说一说该函数图象的特征。 想一想:反比例函数与的图象有什么共同特点?有什么不同点?不同点由什么决定?他们有什么联系?
设计意图 让学生亲自动手操作,会画反比例函数的图像,可以培养学生的动手能力,激发学生学好数学的兴趣,去为发现反比例函数的性质做准备。分组画图的目的是为后面的合作交流做铺垫。采用彩色笔,通过颜色变化,有利于反映和发现问题。
教学环节 (三) 师生活动 归纳与小结:反比例函数的图象和性质: 函数图象形状( )图象位置图象变化趋势
设计意图 通过学生自由讨论、总结、概括本节所学习的内容,使学生进一步了解反比例函数的图象及其性质,让他们体验到学习数学的快乐,在交流中与全班同学分享。
教学环节 (四) 师生活动 基础闯关 1.反比例函数的图象大致是( ) 2.已知反比例函数 若函数的图象位于第一三象限,则k_____________; 若在每一象限内,y随x增大而增大,请写出一个符合条件的k的值: 画出函数的图象: x…-8-5-4-2-112458…y……
(1)列表(填空): (2)描点连线: (3)由图象可知,函数也由 条曲线组成,分别位于第 象限,试猜想:的图象位于第 象限.
设计意图 检验学生对本课知识的掌握及应用情况。通过练习,既培养学生思维的敏捷性,又激发学生的参与和竞争意识.在回答过程中,教师给予适当评讲,并积极调动学生的参与热情,让整个课堂充满活跃的气氛.
教学环节 (五) 师生活动 中考链接 1.已知k<0,则函数在同一坐标系中的图象大致是( ) 思考:把条件“k<0”改为“k≠0”结果还是一样吗? 2.已知反比例函数的图象在第二、四象限,那么一次函数y=kx-k的图象经过( ) A.第一、二、三象限 B.第一、二、四象限 C.第一、三、四象限 D.第二、三、四象限 3.函数与在同一平面直角坐标系中的图象可能是( ) 4.(2017江西)如图,直线与双曲线相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将沿OP方向平移,使点O移动到点P,得到 .过点A'作轴交双曲线于点C。 (1)求k1与k2的值。 (2)求直线PC的表达式。 (3)直接写出线段AB扫过的面积。
设计意图 链接中考,让学生巩固本节知识的同时,综合运用反比例、一次函数、二次函数、图形的变换等知识,提前接触中考题,感受中考题来源于平时练习,可帮助考生掌握中考题目类型及部分考点,研究中考试题的解题方法和技巧,总结中考题的做题思路。
板书设计 26.1.2 反比例函数的图象和性质 1. xy=k y=kx-1 2.与 (k>0) x…-12-6-4-3-2-11234612……-0.5-1-1.5-2-3-66321.510.5……-1-2-3-4-6-121264321…
3.性质:(1)①轴对称图形,对称轴是直线y=x与y=-x。②中心对称图形。 函数图象形状( )图象位置图象变化趋势
③与关于x轴和y轴对称。④双曲线无限接近x轴和y轴,但不与其相交。 (2) 4.思想与方法:数形结合、分类讨论、从特殊到一般、类比。
教学反思 1、同桌互动画图象,改变传统的被动接受知识的教学方式,鼓励学生自己探索、合作交流。对于我班部分个别学生来说画图技巧较弱,课后需再加强辅导。 2、由于本节课的内容与正比例函数有着密切联系,学生能在旧知识中寻找模型,而最后的运用新知、拓展训练中的中考题,提升了一定的高度,有一小部分同学不那么容易理解,需要进行适当的点拨。
