6.2.1 等式的性质与方程的简单变形 课件(2课时、共54张PPT) 2023—2024学年华东师大版数学七年级下册
文档属性
| 名称 | 6.2.1 等式的性质与方程的简单变形 课件(2课时、共54张PPT) 2023—2024学年华东师大版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 20:23:46 | ||
图片预览









文档简介
(共54张PPT)
6.2 解一元一次方程
第1课时 等式的性质
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
思考:要让天平平衡应该满足什么条件?
情境引入
等式的性质
合作探究
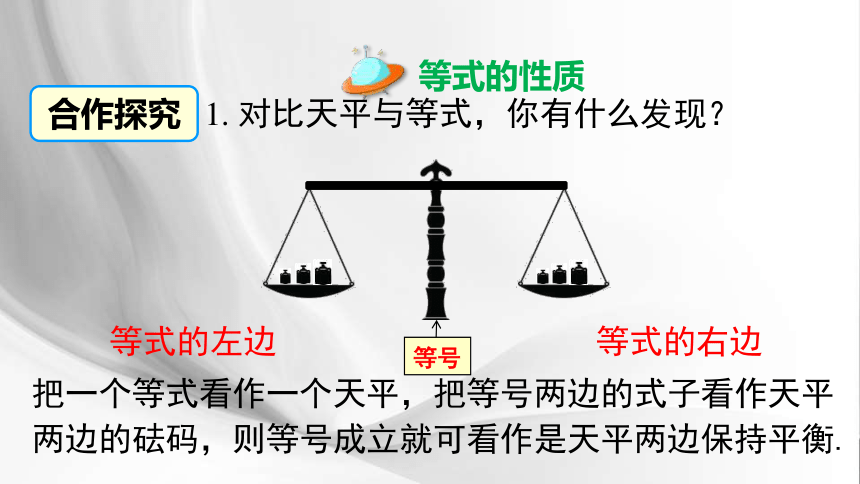
1. 对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平两边保持平衡.
等号
等式的左边
等式的右边
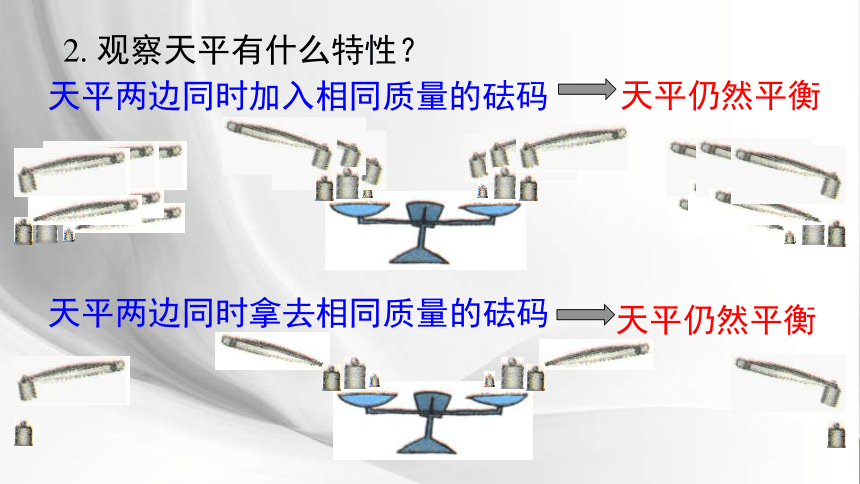
2. 观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
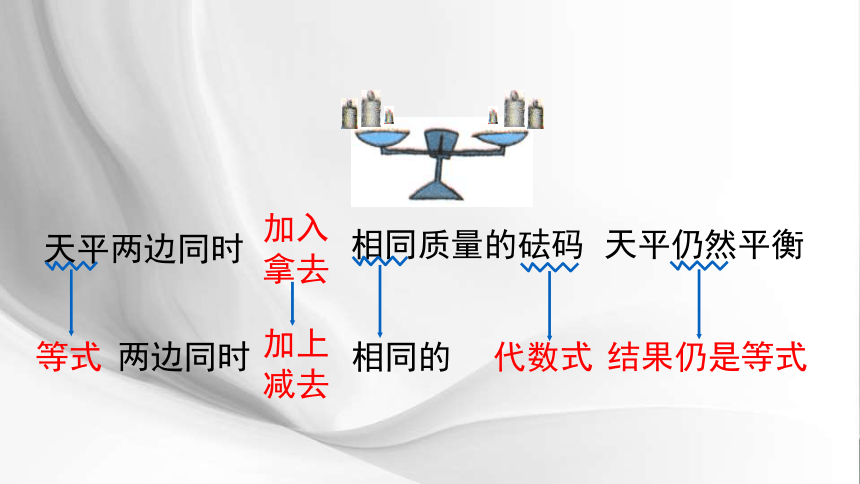
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
两边同时 相同的
等式
加上
减去
代数式
结果仍是等式
等式性质1
结论
等式两边都加上 (或都减去) 同一个数或同一个整式,所得结果仍是等式.
即,如果 a = b,那么
a + c = b + c,a-c = b-c .
由天平特性看等式的基本性质 2
等式两边都乘(或都除以)同一个数(或整式)(除数不能为0),所得结果仍是等式.
如果 a = b,那么 ac = bc,
等式性质2
结论
例1 填空,并说明理由.
(1) 如果 a+2 = b+7,那么 a = ( );
(2) 如果 3x = 9y,那么 x = ( );
(3) 如果 ,那么 3a = ( ).
典例精析
(1) 如果 a+2 = b+7,那么 a = ( );
解:因为 a+2 = b+7 ,由等式性质 1 可知,
等式两边都减去 2,得
a + 2 - 2 = b + 7 - 2,
即 a = b + 5.
(2) 如果 3x = 9y,那么 x = ( );
解:因为 3x = 9y,由等式性质 2 可知,
等式两边都除以3,得 .
即 x = 3y.
b + 5
3y
等式性质 1
等式性质 2
解:因为 ,由等式性质 2 可知,
等式两边都乘 6,得
即 3a = 2b .
2b
(3) 如果 ,那么 3a = ( ).
等式性质 2
请在括号中写出下列等式变形的理由:
(1)如果 a-3 = b+4,那么 a = b+7 ( );
(2)如果 3x = 2y,那么 ( );
等式性质 1
等式性质 2
(3)如果 ,那么 x = 2y ( );
等式性质 2
(4)如果 2a+3 = 3b-1,那么 2a-6 = 3b-10( ).
等式性质 1
练一练
例2 判断下列等式变形是否正确,并说明理由.
(1)如果 a-3=2b-5,那么 a = 2b-8;
(2)如果 ,那么 10x-5 = 16x-8.
解:(1)错误. 由等式性质 1 可知,等式两边都加上 3,
得 a-3+3 = 2b-5+3
即 a = 2b-2 .
(2)正确. 由等式性质 2 可知,等式两边都乘 20,
得 ,即 5(2x-1) = 4(4x-2)
去括号,得 10x-5 = 16x-8.
判断下列等式变形是否正确,并说明理由.
(1)若 ,则 a+3 = 3b-3;
不正确,应该是 a+9 = 3b-3.
(2)若 2x-6 = 4y-2,则 x-3 = 2y-2.
不正确,应该是 x-3 = 2y-1.
练一练
D
1. 如果 ac = ab,那么下列等式中不一定成立的是 ( )
A. ac-1 = ab-1 B. ac+a = ab+a
C. -3ac = -3ab D. c = b
2. 下列变形中,不正确的是 ( )
A. 由 y+3 = 5,得 y = 5-3
B. 由 3y = 4y+2,得 3y-4y = 2
C. 由 y = -2y+1,得 y +2y = 1
D. 由 -y = 6y+3,得 y-6y = 3
D
3. 下列等式变形正确的是 ( )
A. 若 x = y,则
B. 若 a = b,则 a-3 = 3-b
C. 若 2πR = 2πr,则 R = r
D. 若 ,则 a = c
C
4. 下列结论中不能由 a+b = 0 得的是 ( )
A. a2 = -ab B. |a| = |b|
C. a = 0,b = 0 D. a2 = b2
C
等式的基本性质
等式的基本性质
利用等式的基本性质对等式进行变形
6.2 解一元一次方程
第2课时 方程的简单变形
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
复习引入
等式性质1
等式两边同时加上(或都减去)同一个整式,所得结果仍是等式.
即,如果 a = b,那么
a + c = b + c,a-c = b-c .
等式两边都乘(或都除以)同一个数(或整式)(除数不能为0),所得结果仍是等式.
如果 a = b,那么 ac = bc,
等式性质2
请利用等式的性质,把方程 2345 + 12x = 5129 变形成 x = a (其中 a 是已知数)的形式.
①
在方程 ① 两边都减去 2345,
得 2345+12x-2345 = 5129-2345
即 12x = 2784. ②
方程 ② 两边都除以 12,得 x = 232 .
移项
+ 12x = 5129
2345
12x = 5129
-2345
在上面的问题中,我们根据等式性质 1,在方程 ① 两边都减去 2345,相当于作了如下变形:
这个变形有什么特点?
把原方程中的某一项改变________后,从________的一边移到________,这种变形叫做移项.
(1) 移项的根据是等式的基本性质 1.
(2) 移项要变号,没有移动的项不改变符号.
(3) 通常把含有未知数的项移到方程的左边,把常数项(不含未知数的项)移到方程的右边.
移项要点:
符号
方程
另一边
总结归纳
(1) 5+x=10 移项得x= 10+5 ;
(2) 6x=2x+8 移项得 6x+2x =8;
(3) 5-2x=4-3x 移项得3x-2x=4-5;
(4) -2x+7=1-8x 移项得-2x+8x=1-7.
做一做
×
×
√
√
10-5
6x-2x
下面的移项对不对?如果不对,应怎样改正?
1. 移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从 2+5x=7 得到 5x=7+2是不对的.
2. 没移项时不要误认为移项,如从-8=x 得到 x=8,犯这样的错误,其原因在于对等式的基本性质与移项的区别没有分清.
总结归纳
例1 解下列方程:
4x+3 = 2x-7 .
利用移项解一元一次方程
4x
+ 3
=
2 x
-7
4x
-2x
=
-3
-7
典例精析
解:
原方程为 4x+3 = 2x-7
将同类项放在一起
合并同类项,得 2x = -10
移项,得 4x -2x = -7-3
所以 x = -5 是原方程的解.
检验:把 x = -5 分别代入原方程的左、右两边,
左边= 4×(-5)+3 = -17,
右边= 2×(-5)-7 = -17,
左边 = 右边
计算结果
进行检验
两边都除以 2,得 x = -5
提示:以上解一元一次方程的检验过程可以省略.
例 2 解下列方程:
解:方程两边都除以 (或都乘 ),得
即
(1) 移项;
利用移项解方程的步骤是:
(3) 化未知数的系数为 1.
(2) 合并同类项;
归纳总结:
1. (1) 由等式 x-10 = 15 的两边都 ,得到等式
x = 5,这是根据 ;
(2) 由等式 的两边都 ,得到等式 x = ,这是根据 .
加10
等式基本性质 1
等式基本性质 2
乘 -3
D
2. 方程 3x-1 = 5 的解是 ( )
A. B.
C. x = 18 D. x = 2
D
3. 若关于 x 的方程 2x+a-9 = 0 的解是 x = 2,则 a 的值为 ( )
A. 2 B. 3
C. 4 D. 5
(1) 一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
(2) 移项的依据是等式的性质 1.
2. 解形如“ax+b = cx+d ”的方程的一般步骤:
(1) 移项;
(2) 合并同类项;
(3) 化未知数的系数为 1.
1. 移项
6.2 解一元一次方程
第3课时 利用方程的变形求方程的解
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
复习引入
(1) 移项;
利用移项解方程的步骤是:
(3) 化未知数的系数为 1.
(2) 合并同类项;
4x – 15 = 9
用移项解一元一次方程
典例精析
4x= 9+15.
例1 请运用等式的性质解下列方程.
(1) 4x-15 = 9
解:两边都减去 5x,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
+ 15
+ 15
–5x
–5x
4x-15 = 9
4x = 9+15
2x = 5x -21
2x-5x= -21
2x -5x = -21.
4x -15 = 9
①
4x = 9 +15
②
由方程 ① 到方程 ② ,这个变形相当于把 ① 中的 “–15”这一项从方程的左边移到了方程的右边,这一项移动后,发生了什么变化?
-15
4x-15 = 9
4x = 9+15
改变了符号.
由方程 ③ 到方程 ④ ,这个变形相当于把 ③ 中的 “5x”这一项从方程的右边移到了方程的左边,这一项这项移动后,发生了什么变化
改变了符号.
2x = 5x -21
③
2x -5x = -21
④
5x
2x = 5x -21
2x-5x= -21
例2 解方程
解:移项,得
合并同类项 ,得
系数化为 1,得
移项实际上是利用等式的性质 1,但是解题步骤更为简捷!
(1) 8x = 2x-7 ; (2) 6 = 8+2x
解:(1) 移项得 8x-2x =-7
即 6x = -7
两边同时除以 6 得
(2) 移项得 6-8 = 2x
即 -2 = 2x
两边同时除以 2 得
-1 = x
即 x = -1
例3 解方程
(3)
解:移项,得
即
两边都除以 ,得
练一练
解下列方程:
(1) 2.5x+318 = 1068;
(2) 2.4y + 2y+2.4 = 6.8.
x = 300
y = 1
1. 解下列一元一次方程:
答案:(1) x = -2 (2) t = 20
(3) x = -4 (4) x = 2
解形如“ax+b = cx+d ”的方程的一般步骤:
(1) 移项;
(2) 合并同类项;
(3) 化未知数的系数为 1.
谢谢观看
华东师大版数学七年级下册
6.2 解一元一次方程
第1课时 等式的性质
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
思考:要让天平平衡应该满足什么条件?
情境引入
等式的性质
合作探究
1. 对比天平与等式,你有什么发现?
把一个等式看作一个天平,把等号两边的式子看作天平两边的砝码,则等号成立就可看作是天平两边保持平衡.
等号
等式的左边
等式的右边
2. 观察天平有什么特性?
天平两边同时加入相同质量的砝码
天平仍然平衡
天平两边同时拿去相同质量的砝码
天平仍然平衡
天平两边同时
天平仍然平衡
加入
拿去
相同质量的砝码
两边同时 相同的
等式
加上
减去
代数式
结果仍是等式
等式性质1
结论
等式两边都加上 (或都减去) 同一个数或同一个整式,所得结果仍是等式.
即,如果 a = b,那么
a + c = b + c,a-c = b-c .
由天平特性看等式的基本性质 2
等式两边都乘(或都除以)同一个数(或整式)(除数不能为0),所得结果仍是等式.
如果 a = b,那么 ac = bc,
等式性质2
结论
例1 填空,并说明理由.
(1) 如果 a+2 = b+7,那么 a = ( );
(2) 如果 3x = 9y,那么 x = ( );
(3) 如果 ,那么 3a = ( ).
典例精析
(1) 如果 a+2 = b+7,那么 a = ( );
解:因为 a+2 = b+7 ,由等式性质 1 可知,
等式两边都减去 2,得
a + 2 - 2 = b + 7 - 2,
即 a = b + 5.
(2) 如果 3x = 9y,那么 x = ( );
解:因为 3x = 9y,由等式性质 2 可知,
等式两边都除以3,得 .
即 x = 3y.
b + 5
3y
等式性质 1
等式性质 2
解:因为 ,由等式性质 2 可知,
等式两边都乘 6,得
即 3a = 2b .
2b
(3) 如果 ,那么 3a = ( ).
等式性质 2
请在括号中写出下列等式变形的理由:
(1)如果 a-3 = b+4,那么 a = b+7 ( );
(2)如果 3x = 2y,那么 ( );
等式性质 1
等式性质 2
(3)如果 ,那么 x = 2y ( );
等式性质 2
(4)如果 2a+3 = 3b-1,那么 2a-6 = 3b-10( ).
等式性质 1
练一练
例2 判断下列等式变形是否正确,并说明理由.
(1)如果 a-3=2b-5,那么 a = 2b-8;
(2)如果 ,那么 10x-5 = 16x-8.
解:(1)错误. 由等式性质 1 可知,等式两边都加上 3,
得 a-3+3 = 2b-5+3
即 a = 2b-2 .
(2)正确. 由等式性质 2 可知,等式两边都乘 20,
得 ,即 5(2x-1) = 4(4x-2)
去括号,得 10x-5 = 16x-8.
判断下列等式变形是否正确,并说明理由.
(1)若 ,则 a+3 = 3b-3;
不正确,应该是 a+9 = 3b-3.
(2)若 2x-6 = 4y-2,则 x-3 = 2y-2.
不正确,应该是 x-3 = 2y-1.
练一练
D
1. 如果 ac = ab,那么下列等式中不一定成立的是 ( )
A. ac-1 = ab-1 B. ac+a = ab+a
C. -3ac = -3ab D. c = b
2. 下列变形中,不正确的是 ( )
A. 由 y+3 = 5,得 y = 5-3
B. 由 3y = 4y+2,得 3y-4y = 2
C. 由 y = -2y+1,得 y +2y = 1
D. 由 -y = 6y+3,得 y-6y = 3
D
3. 下列等式变形正确的是 ( )
A. 若 x = y,则
B. 若 a = b,则 a-3 = 3-b
C. 若 2πR = 2πr,则 R = r
D. 若 ,则 a = c
C
4. 下列结论中不能由 a+b = 0 得的是 ( )
A. a2 = -ab B. |a| = |b|
C. a = 0,b = 0 D. a2 = b2
C
等式的基本性质
等式的基本性质
利用等式的基本性质对等式进行变形
6.2 解一元一次方程
第2课时 方程的简单变形
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
复习引入
等式性质1
等式两边同时加上(或都减去)同一个整式,所得结果仍是等式.
即,如果 a = b,那么
a + c = b + c,a-c = b-c .
等式两边都乘(或都除以)同一个数(或整式)(除数不能为0),所得结果仍是等式.
如果 a = b,那么 ac = bc,
等式性质2
请利用等式的性质,把方程 2345 + 12x = 5129 变形成 x = a (其中 a 是已知数)的形式.
①
在方程 ① 两边都减去 2345,
得 2345+12x-2345 = 5129-2345
即 12x = 2784. ②
方程 ② 两边都除以 12,得 x = 232 .
移项
+ 12x = 5129
2345
12x = 5129
-2345
在上面的问题中,我们根据等式性质 1,在方程 ① 两边都减去 2345,相当于作了如下变形:
这个变形有什么特点?
把原方程中的某一项改变________后,从________的一边移到________,这种变形叫做移项.
(1) 移项的根据是等式的基本性质 1.
(2) 移项要变号,没有移动的项不改变符号.
(3) 通常把含有未知数的项移到方程的左边,把常数项(不含未知数的项)移到方程的右边.
移项要点:
符号
方程
另一边
总结归纳
(1) 5+x=10 移项得x= 10+5 ;
(2) 6x=2x+8 移项得 6x+2x =8;
(3) 5-2x=4-3x 移项得3x-2x=4-5;
(4) -2x+7=1-8x 移项得-2x+8x=1-7.
做一做
×
×
√
√
10-5
6x-2x
下面的移项对不对?如果不对,应怎样改正?
1. 移项时必须是从等号的一边到另一边,并且不要忘记对移动的项变号,如从 2+5x=7 得到 5x=7+2是不对的.
2. 没移项时不要误认为移项,如从-8=x 得到 x=8,犯这样的错误,其原因在于对等式的基本性质与移项的区别没有分清.
总结归纳
例1 解下列方程:
4x+3 = 2x-7 .
利用移项解一元一次方程
4x
+ 3
=
2 x
-7
4x
-2x
=
-3
-7
典例精析
解:
原方程为 4x+3 = 2x-7
将同类项放在一起
合并同类项,得 2x = -10
移项,得 4x -2x = -7-3
所以 x = -5 是原方程的解.
检验:把 x = -5 分别代入原方程的左、右两边,
左边= 4×(-5)+3 = -17,
右边= 2×(-5)-7 = -17,
左边 = 右边
计算结果
进行检验
两边都除以 2,得 x = -5
提示:以上解一元一次方程的检验过程可以省略.
例 2 解下列方程:
解:方程两边都除以 (或都乘 ),得
即
(1) 移项;
利用移项解方程的步骤是:
(3) 化未知数的系数为 1.
(2) 合并同类项;
归纳总结:
1. (1) 由等式 x-10 = 15 的两边都 ,得到等式
x = 5,这是根据 ;
(2) 由等式 的两边都 ,得到等式 x = ,这是根据 .
加10
等式基本性质 1
等式基本性质 2
乘 -3
D
2. 方程 3x-1 = 5 的解是 ( )
A. B.
C. x = 18 D. x = 2
D
3. 若关于 x 的方程 2x+a-9 = 0 的解是 x = 2,则 a 的值为 ( )
A. 2 B. 3
C. 4 D. 5
(1) 一般地,把方程中的某些项改变符号后,从方程的一边移到另一边,这种变形叫做移项.
(2) 移项的依据是等式的性质 1.
2. 解形如“ax+b = cx+d ”的方程的一般步骤:
(1) 移项;
(2) 合并同类项;
(3) 化未知数的系数为 1.
1. 移项
6.2 解一元一次方程
第3课时 利用方程的变形求方程的解
6.2.1 等式的性质与方程的简单变形
华东师大版数学七年级下册
复习引入
(1) 移项;
利用移项解方程的步骤是:
(3) 化未知数的系数为 1.
(2) 合并同类项;
4x – 15 = 9
用移项解一元一次方程
典例精析
4x= 9+15.
例1 请运用等式的性质解下列方程.
(1) 4x-15 = 9
解:两边都减去 5x,得
-3x=-21.
系数化为1,得
x = 6.
(2) 2x = 5x -21
解:两边都加上 15 ,得
系数化为1,得
x = 7.
合并同类项 ,得
合并同类项 ,得
4x = 24.
2x = 5x – 21
+ 15
+ 15
–5x
–5x
4x-15 = 9
4x = 9+15
2x = 5x -21
2x-5x= -21
2x -5x = -21.
4x -15 = 9
①
4x = 9 +15
②
由方程 ① 到方程 ② ,这个变形相当于把 ① 中的 “–15”这一项从方程的左边移到了方程的右边,这一项移动后,发生了什么变化?
-15
4x-15 = 9
4x = 9+15
改变了符号.
由方程 ③ 到方程 ④ ,这个变形相当于把 ③ 中的 “5x”这一项从方程的右边移到了方程的左边,这一项这项移动后,发生了什么变化
改变了符号.
2x = 5x -21
③
2x -5x = -21
④
5x
2x = 5x -21
2x-5x= -21
例2 解方程
解:移项,得
合并同类项 ,得
系数化为 1,得
移项实际上是利用等式的性质 1,但是解题步骤更为简捷!
(1) 8x = 2x-7 ; (2) 6 = 8+2x
解:(1) 移项得 8x-2x =-7
即 6x = -7
两边同时除以 6 得
(2) 移项得 6-8 = 2x
即 -2 = 2x
两边同时除以 2 得
-1 = x
即 x = -1
例3 解方程
(3)
解:移项,得
即
两边都除以 ,得
练一练
解下列方程:
(1) 2.5x+318 = 1068;
(2) 2.4y + 2y+2.4 = 6.8.
x = 300
y = 1
1. 解下列一元一次方程:
答案:(1) x = -2 (2) t = 20
(3) x = -4 (4) x = 2
解形如“ax+b = cx+d ”的方程的一般步骤:
(1) 移项;
(2) 合并同类项;
(3) 化未知数的系数为 1.
谢谢观看
华东师大版数学七年级下册
