6.3 实践与探索 课件(3课时、共66张PPT) 2023—2024学年华东师大版数学七年级下册
文档属性
| 名称 | 6.3 实践与探索 课件(3课时、共66张PPT) 2023—2024学年华东师大版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 8.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 20:31:21 | ||
图片预览








文档简介
(共66张PPT)
6.3 实践与探索
第1课时 等积变形问题
华东师大版数学七年级下册
情境引入
从一个水杯向另一个水杯倒水.
思考:在这个过程中什么没有发生变化?
图形的等长变化
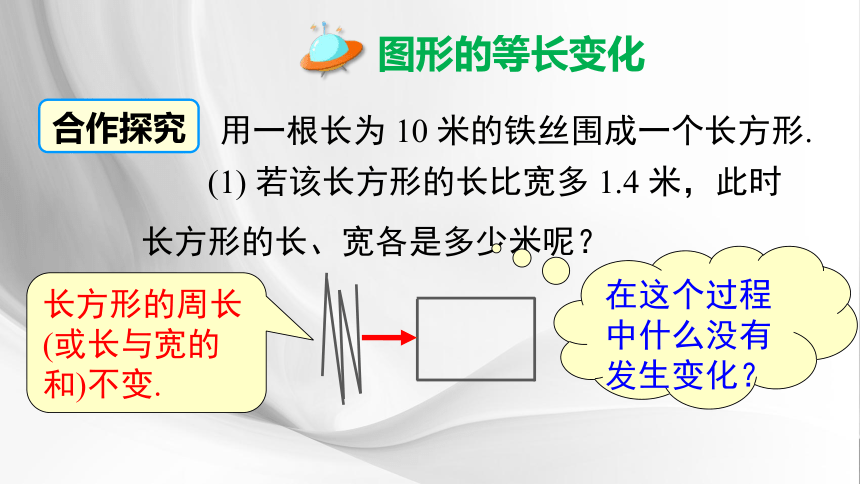
合作探究
(1) 若该长方形的长比宽多 1.4 米,此时长方形的长、宽各是多少米呢?
在这个过程中什么没有发生变化?
长方形的周长(或长与宽的和)不变.
用一根长为 10 米的铁丝围成一个长方形.
x m
(x+1.4) m
等量关系:
(长+宽)× 2 = 周长
解: 设此时长方形的宽为 x 米,则它的长为 (x+1.4) 米. 根据题意,得
(x+1.4 +x) ×2 =10
解得 x = 1.8
长:1.8+1.4 = 3.2
此时长方形的长为 3.2 米,宽为 1.8 米.
(2) 若该长方形的长比宽多 0.8 米,此时长方形的长和宽各为多少米?它围成的长方形与 (1) 中所围成的长方形相比,面积有什么变化?
解:设此时长方形的宽为 x m,则它的长为(x+0.8) m.根据题意,得
(x+0.8+x)×2 = 10
解得 x = 2.1
长:2.1+0.8 = 2.9
此时长方形的长为 2.9 m,宽为 2.1 m,面积为
2.9×2.1 = 6.09 (m2),(1) 中长方形的面积为 3.2×1.8 = 5.76 (m2).
此时长方形的面积比 (1) 中长方形的面积增大 6.09-5.76 = 0.33 (m2).
(3) 若该长方形的长与宽相等,即围成一个正方形,则正方形的边长是多少?它围成的正方形的面积与 (2) 中相比,又有什么变化?
x m
(x+x) ×2 = 10
解得 x = 2.5
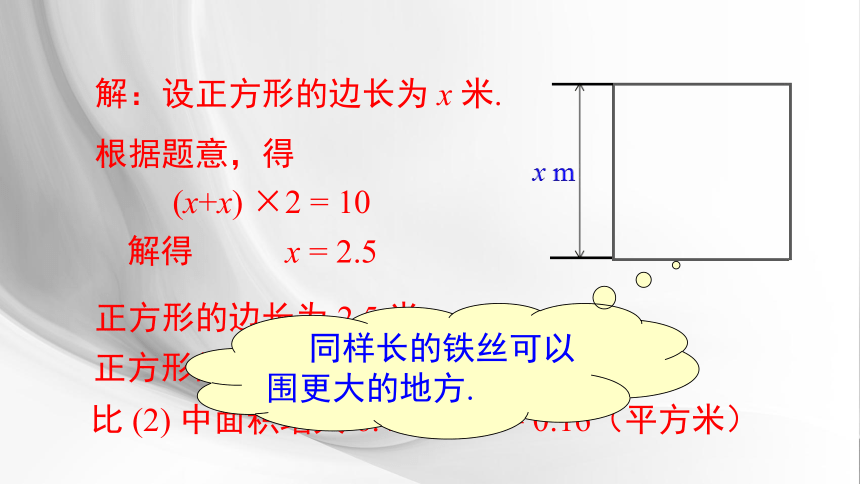
正方形的面积为 2.5 × 2.5 = 6.25 (平方米)
解:设正方形的边长为 x 米.
根据题意,得
比 (2) 中面积增大 6. 25-6.09 = 0.16(平方米)
正方形的边长为 2.5 米
同样长的铁丝可以围更大的地方.
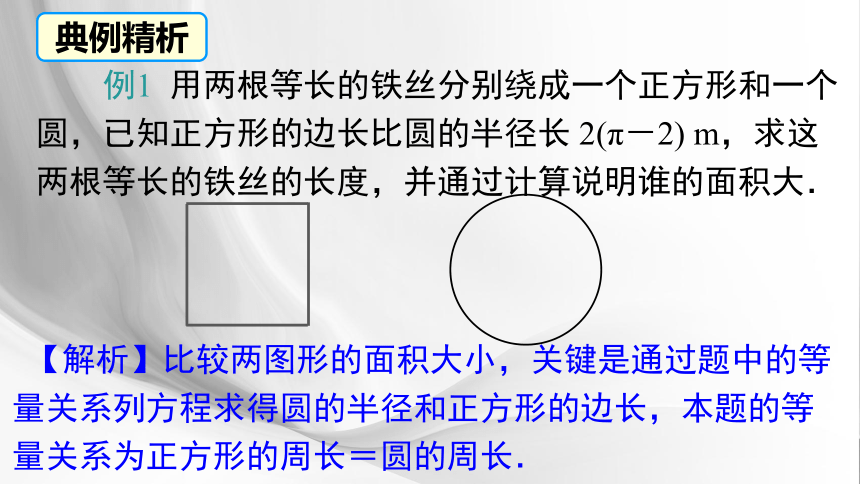
例1 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长 2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
典例精析
【解析】比较两图形的面积大小,关键是通过题中的等量关系列方程求得圆的半径和正方形的边长,本题的等量关系为正方形的周长=圆的周长.
解:设圆的半径为 r m,则正方形的边长为
[r+2(π-2)] m.根据题意,得
答:铁丝的长为 8π m,圆的面积较大.
因为 4π×4 > 4π×π,所以 16π > 4π2,
所以圆的面积大.
正方形的面积为 [4+2(π-2)]2 = 4π2(m 2).
所以圆的面积是 π×42 = 16π(m 2),
所以铁丝的长为 2πr = 8π(m).
2πr = 4(r+2π-4),解得 r = 4.
(1) 形状、面积发生了变化,而周长没变;
(2) 形状、周长不同,但是根据题意找出周长之间的关系,把这个关系作为等量关系.解决问题的关键是通过分析变化过程,挖掘其等量关系,从而可列方程.
归纳总结
图形的等积变化
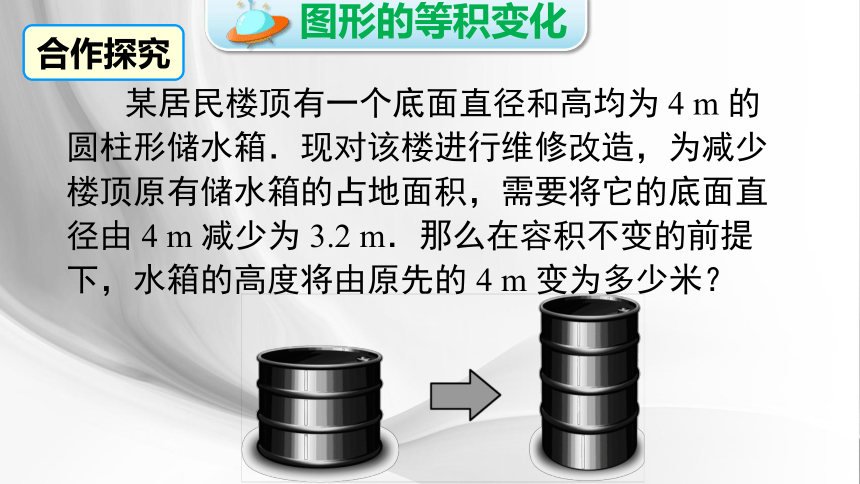
某居民楼顶有一个底面直径和高均为 4 m 的圆柱形储水箱.现对该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由 4 m 减少为 3.2 m.那么在容积不变的前提下,水箱的高度将由原先的 4 m 变为多少米?
合作探究
1. 如果设水箱的高变为 x m,填写下表:
旧水箱 新水箱
底面半径/m
高/m
体积/m
2
1.6
4
x
π×22×4
π×1.62×x
3. 列出方程并求解.
2. 根据表格中的分析,找出等量关系.
旧水箱的容积 = 新水箱的容积
π×22×4
π×1.62×x
=
解得 x = 6.25
因此,水箱的高度变成了 6.25 m.
例2 一种牙膏出口处直径为 5 mm,小明每次刷牙都挤出 1 cm 长的牙膏,这样一支牙膏可以用 36 次,该品牌牙膏推出新包装,只是将出口处直径改为 6 mm,小明还是按习惯每次挤出 1 cm 的牙膏,这样,这一支牙膏能用多少次?
解:设这一支牙膏能用 x 次,根据题意得
解这个方程,得 x = 25.
答:这一支牙膏能用 25 次.
你认为列一元一次方程解应用题的主要步骤有哪些?关键是什么?
思考:
1. 审——通过审题找出等量关系.
6. 答——注意单位名称.
5. 检——检验求出的值是否为方程的解,并检验是否符
合实际问题.
4. 解——求出方程的解(对间接设的未知数切忌继续求解).
3. 列——依据找到的等量关系,列出方程.
2. 设——设出合理的未知数(直接或间接),注意单位名称.
做一做
1. 要锻造一个直径为 8 厘米、高为 4 厘米的圆柱形毛坯,则至少应截取直径为 4 厘米的圆钢______厘米.
2. 钢锭的截面是正方形,其边长是 20 厘米,要锻造成长、宽、高分别为 40 厘米、30 厘米、10 厘米的长方体,则应截取这种钢锭多长?
答:应截取这种钢锭 30 厘米.
16
1. 一个长方形的周长是 40 cm,若将长减少 8 cm,宽增加 2 cm,长方形就变成了正方形,则正方形的边长为 ( )
A. 6 cm B. 7 cm
C. 8 cm D. 9 cm
B
C
2. 一个梯形的面积是 60 cm2,高为 5 cm,它的上底比下底短 2 cm,求这个梯形上底和下底的长度.设下底长为 x cm,则下面所列方程正确的是 ( )
3. 根据图中给出的信息,可得正确的方程是 ( )
A
A. π×42x = π×32×(x+5) B. π×42x = π×32×(x-5)
C. π×82x = π×62×(x+5) D. π×82x = π×62×(x-5)
应用一元一次方程
图形等长变化
应用一元一次方程解决实际问题的步骤
图形等积变化
列
⑤检
④解
设
审
⑥答
6.3 实践与探索
第2课时 销售问题及百分率问题
华东师大版数学七年级下册
情境引入
清仓处理
跳楼价
满200返100
五折销售
销售中的盈亏
合作探究
1. 进价 100 元的商品提价 40% 后,标价为________元,若按标价的八折销售,则售价为________元,此商品的利润为________元,利润率是________.
2. 某商品原价是 a 元,现在每件打九折销售,则此时的售价是 元.
3. 一件商品打 x 折出售,就是用原价乘 .
140
112
12
0.9a
12%
填空:
问题1:上面的打折销售问题中有哪些量
成本价(进价)
标价(原价)
销售价
利润
利润率
问题2:这些量有何关系
大家想一想!
进价:购进商品时的价格(有时也叫成本价).
售价:在销售商品时的售出价(有时称成交价,卖出价).
标价:在销售时标出的价(有时称原价,定价).
利润:在销售商品的过程中的纯收入,利润=售价-进价.
有关销售的概念
利润率:利润占进价的百分率,即:
利润率 = 利润÷进价×100%.
概念学习
理一理:打折促销活动中各个量与量之间有怎样的等量关系?
进价+提价 = 标价
售价-进价(成本)= 利润
进价×利润率 = 利润
标价×折扣率 = 售价
打折或减价
标价
售价
进价
提价
利润、利润率
(1) 某商品的进价为 80 元,在进价的基础上提高 20% 后标价,则标价为 元.
(2) 标价为 500 元的商品打 9 折后的售价为 元.
(3) 某商品每件的销售利润是 72 元,进价是 120 元,则售价是 元.
(4) 某商品利润率为 13%,进价为 50 元,则利润是
元.
(80+80×20%)
(500×0.9)
(50×13%)
(120+72)
96
450
6.5
192
做一做
商品利润
利润率 =
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价 =
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价 =
×(1 + 利润率)
打
折
销
售
要点归纳
A. 盈利
B. 亏损
C. 不盈不亏
你估计盈亏情况是怎样的?
典例精析
例1 一商店在某一时间以每件 60 元的价格卖出两件衣服,其中一件盈利 25% ,另一件亏损 25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
¥60
¥60
思考:销售的盈亏决定于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价 > 总成本
总售价 < 总成本
总售价 = 总成本
盈 利
亏 损
不盈不亏
(2) 设亏损 25% 的衣服进价是 y 元,
依题意得 y-0.25y = 60
解得 y = 80
(1) 设盈利 25% 的衣服进价是 x 元,
依题意得 x+0.25 x = 60
解得 x = 48
解:
两件衣服总成本:x+y = 48+80 =128(元)
因为 120-128 = -8(元)
所以卖这两件衣服共亏损了 8 元.
与你猜想的一致吗?
1. 某琴行同时卖出两台钢琴,每台售价为 960 元.其中一台盈利 20%,另一台亏损 20%.这次琴行是盈利还是亏损,或是不盈不亏?
练一练
2. 某文具店有两个进价不同的计算器都卖 64 元,其中一个盈利 60%,另一个亏本 20%.这次交易中的盈亏情况?
答案:买这两个计算器盈利 8 元.
答案:这次琴行亏本 80 元.
例2 一件服装先将进价提高 25% 出售,后进行促销活动,又按标价的 8 折出售,此时售价为 60 元. 请问商家是盈是亏,还是不盈不亏?
解:设这件衣服的进价是 x 元,
则提价后的售价是 (1+25%)x 元,
促销后的售价是 (1+25%)x×0.8 元,
依题意得 (1+25%)x×0.8 = 60
解得 x = 60
售价 60 = 成本 60 答:这家商店不盈不亏.
练一练
1. 某商品在原价的基础上提高 25% 标价,若想调回原价,应降价的百分率为 .
20%
2. 我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品在 2021 年涨价 30% 后,2023 年降价 70% 至 a 元,则这种药品在 2005 年涨价前价格为 元.
1. 某商品的进价是 1000 元,售价是 1500 元,由于销售情况不好,商店决定降价出售,但又要保证利润率不低于 5%,那么商店最多可打几折出售此商品?
解:设商店最多可以打 x 折出售此商品,
根据题意,得
1500× = 1000(1+5%)
解得 x = 7
答:商店最多可以打 7 折出售此商品.
2. 据了解个体商店销售中售价只要高出进价的 20% 便可盈利,但老板们常以高出进价 50% ~ 100% 标价,假若你准备买一双标价为 600 元的运动鞋,应在什么范围内还价?
高于进价 50% 标价 高于进价 100% 标价
进价 x 元 y 元
标价 (1+50%)x (1+100%)y
方程 (1+50%)x = 600 (1+100%)y = 600
方程的解 x = 400 y = 300
盈利价 400(1+20%) = 480 300(1+20%) = 360
答:应在 480 元 ~ 360 元内还价.
商品利润
利润率 =
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价 =
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价 =
×(1 + 利润率)
打
折
销
售
6.3 实践与探索
第 3 课时 速率问题
华东师大版数学七年级下册
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
相遇问题
星期天早晨,小斌和小强分别骑自行车从家里同时出发去参观雷锋纪念馆. 已知他俩的家到雷锋纪念馆的路程相等,小斌每小时骑 10 km,他在上午 10 时到达;小强每时骑 15 km,他在上午 9 时 30 分到达.求他们的家到雷锋纪念馆的路程.
情境引入
由于小斌的速度较慢,因此他花的时间比小强花的时间多.
本问题中涉及的等量关系有:
.
因此,设他俩的家到雷锋纪念馆的路程均为 s km,
解得 s = ____.
因此,小斌和小强的家到雷锋纪念馆的路程为 km.
根据等量关系,得
.
15
15
注意单位要统一.
例1 小明与小红的家相距 20 km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为 13 km/h,小红骑车的速度是 12 km/h.
(1) 如果两人同时出发,那么他们经过多少小时相遇?
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.即
小明走的路程+小红走的路程 = 两家之间的距离(20 km).
典例精析
解:设小明与小红骑车走了 x h 后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过 0.8 h 他们两人相遇.
小明走的路程
小红走的路程
(2) 如果小明先走 30 min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:设小红骑车走了 t h 后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走 0.54 h 后与小明相遇.
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
相遇问题
总结归纳
注意相向而行的始发时间和地点.
甲、乙两车分别从 A,B 两地同时出发,相向而行.已知 A,B 两地的距离为 480 km,且甲车以 65 km/ h 的速度行驶.若两车 4 h 后相遇,则乙车的行驶速度是多少?
答:乙车的行驶速度是 55 km/h.
练一练
例2 小明早晨要在 7:20 以前赶到距家 1000 米的学校上学.一天,小明以 80 米/分钟的速度出发,5 分钟后,小明的爸爸发现他忘了带历史作业,于是,爸爸立即以 180 米/分钟的速度去追小明,并且在途中追上了他.
问爸爸追上小明用了多长时间?
分析:当爸爸追上小明时,两人所走路程相等.
追及问题
解:设爸爸追上小明用了 x 分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x = 180x.
答:爸爸追上小明用了 4 分钟.
解得 x = 4.
80×5
80x
180x
一队学生步行去郊外春游,每小时走 4 km,学生甲因故推迟出发 30 min,为了赶上队伍,甲以 6 km/h的速度追赶,问甲用多少时间就可追上队伍?
答:该生用了 1 小时追上了队伍.
练一练
路程 = 速度×时间
S快-S慢 = S原来距离
追及问题
总结归纳
注意同向而行始发时间和地点.
例3 生产的这批螺钉、螺母要打包,由一个人做要 40 h 完成.现计划由一部分人先做 4 h,然后增加 2 人与他们一起做 8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
工作量之和等于总工作量 1 .
工程问题
×
×
=
解:设先安排 x 人做 4 h,根据题意得等量关系:
可列方程
解方程,得 4x+8(x+2)=40,
4x+8x+16=40,
12x = 24,
x = 2.
答:应先安排 2人做 4 小时.
前部分工作总量+后部分工作总量=总工作量 1
一条地下管线由甲工程队单独铺设需要 12 天,由乙工程队单独铺设需要 24 天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
做一做
根据工作效率×工作时间 = 工作量,列方程:
解:设要 x 天可以铺好这条管线,由题意得
答:要 8 天可以铺好这条管线.
分析:把工作量看作单位“1”,则甲的工作效率为 ,乙的工作效率为 .
解方程,得
解决工程问题的思路:
1. 三个基本量:
三个基本量:工作量、工作效率、工作时间.
工作量=工作效率×工作时间.
若把工作量看作 1 ,则工作效率 =
2. 相等关系:
(1) 按工作时间,各时间段的工作量之和 = 完成的工作量.
(2) 按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量 = 完成的工作量.
要点归纳
1.甲每小时走 5 千米,甲出发 4.5 小时后,乙骑车从同一地点出发追赶甲,乙用了 35 分钟追上甲,设乙骑车的速度为 x 千米/时,则所列方程为( )
B
2.甲、乙两人骑摩托车同时从相距 170 千米的 A,B 两地相向而行,2 小时相遇,如果甲比乙每小时多行 5 千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
B
3.甲、乙两人在 400 米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是 6 米/秒,乙的速度是 4 米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
A
4. 一项工作,甲独做需 18 天,乙独做需 24 天,如果两人合做 8 天后,余下的工作再由甲独做 x 天完成,
那么所列方程为____________.
行程问题
路程=速度×时间
相遇问题
追及问题
甲走的路程+乙走的路程 =甲、乙之间的距离
S快-S慢= S原来距离
解决工程问题的思路:
1. 三个基本量:
三个基本量:工作量、工作效率、工作时间.
工作量=工作效率×工作时间.
若把工作量看作 1 ,则工作效率 =
2. 相等关系:
(1) 按工作时间,各时间段的工作量之和 = 完成的工作量.
(2) 按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量 = 完成的工作量.
谢谢观看
华东师大版数学七年级下册
6.3 实践与探索
第1课时 等积变形问题
华东师大版数学七年级下册
情境引入
从一个水杯向另一个水杯倒水.
思考:在这个过程中什么没有发生变化?
图形的等长变化
合作探究
(1) 若该长方形的长比宽多 1.4 米,此时长方形的长、宽各是多少米呢?
在这个过程中什么没有发生变化?
长方形的周长(或长与宽的和)不变.
用一根长为 10 米的铁丝围成一个长方形.
x m
(x+1.4) m
等量关系:
(长+宽)× 2 = 周长
解: 设此时长方形的宽为 x 米,则它的长为 (x+1.4) 米. 根据题意,得
(x+1.4 +x) ×2 =10
解得 x = 1.8
长:1.8+1.4 = 3.2
此时长方形的长为 3.2 米,宽为 1.8 米.
(2) 若该长方形的长比宽多 0.8 米,此时长方形的长和宽各为多少米?它围成的长方形与 (1) 中所围成的长方形相比,面积有什么变化?
解:设此时长方形的宽为 x m,则它的长为(x+0.8) m.根据题意,得
(x+0.8+x)×2 = 10
解得 x = 2.1
长:2.1+0.8 = 2.9
此时长方形的长为 2.9 m,宽为 2.1 m,面积为
2.9×2.1 = 6.09 (m2),(1) 中长方形的面积为 3.2×1.8 = 5.76 (m2).
此时长方形的面积比 (1) 中长方形的面积增大 6.09-5.76 = 0.33 (m2).
(3) 若该长方形的长与宽相等,即围成一个正方形,则正方形的边长是多少?它围成的正方形的面积与 (2) 中相比,又有什么变化?
x m
(x+x) ×2 = 10
解得 x = 2.5
正方形的面积为 2.5 × 2.5 = 6.25 (平方米)
解:设正方形的边长为 x 米.
根据题意,得
比 (2) 中面积增大 6. 25-6.09 = 0.16(平方米)
正方形的边长为 2.5 米
同样长的铁丝可以围更大的地方.
例1 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长 2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
典例精析
【解析】比较两图形的面积大小,关键是通过题中的等量关系列方程求得圆的半径和正方形的边长,本题的等量关系为正方形的周长=圆的周长.
解:设圆的半径为 r m,则正方形的边长为
[r+2(π-2)] m.根据题意,得
答:铁丝的长为 8π m,圆的面积较大.
因为 4π×4 > 4π×π,所以 16π > 4π2,
所以圆的面积大.
正方形的面积为 [4+2(π-2)]2 = 4π2(m 2).
所以圆的面积是 π×42 = 16π(m 2),
所以铁丝的长为 2πr = 8π(m).
2πr = 4(r+2π-4),解得 r = 4.
(1) 形状、面积发生了变化,而周长没变;
(2) 形状、周长不同,但是根据题意找出周长之间的关系,把这个关系作为等量关系.解决问题的关键是通过分析变化过程,挖掘其等量关系,从而可列方程.
归纳总结
图形的等积变化
某居民楼顶有一个底面直径和高均为 4 m 的圆柱形储水箱.现对该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由 4 m 减少为 3.2 m.那么在容积不变的前提下,水箱的高度将由原先的 4 m 变为多少米?
合作探究
1. 如果设水箱的高变为 x m,填写下表:
旧水箱 新水箱
底面半径/m
高/m
体积/m
2
1.6
4
x
π×22×4
π×1.62×x
3. 列出方程并求解.
2. 根据表格中的分析,找出等量关系.
旧水箱的容积 = 新水箱的容积
π×22×4
π×1.62×x
=
解得 x = 6.25
因此,水箱的高度变成了 6.25 m.
例2 一种牙膏出口处直径为 5 mm,小明每次刷牙都挤出 1 cm 长的牙膏,这样一支牙膏可以用 36 次,该品牌牙膏推出新包装,只是将出口处直径改为 6 mm,小明还是按习惯每次挤出 1 cm 的牙膏,这样,这一支牙膏能用多少次?
解:设这一支牙膏能用 x 次,根据题意得
解这个方程,得 x = 25.
答:这一支牙膏能用 25 次.
你认为列一元一次方程解应用题的主要步骤有哪些?关键是什么?
思考:
1. 审——通过审题找出等量关系.
6. 答——注意单位名称.
5. 检——检验求出的值是否为方程的解,并检验是否符
合实际问题.
4. 解——求出方程的解(对间接设的未知数切忌继续求解).
3. 列——依据找到的等量关系,列出方程.
2. 设——设出合理的未知数(直接或间接),注意单位名称.
做一做
1. 要锻造一个直径为 8 厘米、高为 4 厘米的圆柱形毛坯,则至少应截取直径为 4 厘米的圆钢______厘米.
2. 钢锭的截面是正方形,其边长是 20 厘米,要锻造成长、宽、高分别为 40 厘米、30 厘米、10 厘米的长方体,则应截取这种钢锭多长?
答:应截取这种钢锭 30 厘米.
16
1. 一个长方形的周长是 40 cm,若将长减少 8 cm,宽增加 2 cm,长方形就变成了正方形,则正方形的边长为 ( )
A. 6 cm B. 7 cm
C. 8 cm D. 9 cm
B
C
2. 一个梯形的面积是 60 cm2,高为 5 cm,它的上底比下底短 2 cm,求这个梯形上底和下底的长度.设下底长为 x cm,则下面所列方程正确的是 ( )
3. 根据图中给出的信息,可得正确的方程是 ( )
A
A. π×42x = π×32×(x+5) B. π×42x = π×32×(x-5)
C. π×82x = π×62×(x+5) D. π×82x = π×62×(x-5)
应用一元一次方程
图形等长变化
应用一元一次方程解决实际问题的步骤
图形等积变化
列
⑤检
④解
设
审
⑥答
6.3 实践与探索
第2课时 销售问题及百分率问题
华东师大版数学七年级下册
情境引入
清仓处理
跳楼价
满200返100
五折销售
销售中的盈亏
合作探究
1. 进价 100 元的商品提价 40% 后,标价为________元,若按标价的八折销售,则售价为________元,此商品的利润为________元,利润率是________.
2. 某商品原价是 a 元,现在每件打九折销售,则此时的售价是 元.
3. 一件商品打 x 折出售,就是用原价乘 .
140
112
12
0.9a
12%
填空:
问题1:上面的打折销售问题中有哪些量
成本价(进价)
标价(原价)
销售价
利润
利润率
问题2:这些量有何关系
大家想一想!
进价:购进商品时的价格(有时也叫成本价).
售价:在销售商品时的售出价(有时称成交价,卖出价).
标价:在销售时标出的价(有时称原价,定价).
利润:在销售商品的过程中的纯收入,利润=售价-进价.
有关销售的概念
利润率:利润占进价的百分率,即:
利润率 = 利润÷进价×100%.
概念学习
理一理:打折促销活动中各个量与量之间有怎样的等量关系?
进价+提价 = 标价
售价-进价(成本)= 利润
进价×利润率 = 利润
标价×折扣率 = 售价
打折或减价
标价
售价
进价
提价
利润、利润率
(1) 某商品的进价为 80 元,在进价的基础上提高 20% 后标价,则标价为 元.
(2) 标价为 500 元的商品打 9 折后的售价为 元.
(3) 某商品每件的销售利润是 72 元,进价是 120 元,则售价是 元.
(4) 某商品利润率为 13%,进价为 50 元,则利润是
元.
(80+80×20%)
(500×0.9)
(50×13%)
(120+72)
96
450
6.5
192
做一做
商品利润
利润率 =
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价 =
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价 =
×(1 + 利润率)
打
折
销
售
要点归纳
A. 盈利
B. 亏损
C. 不盈不亏
你估计盈亏情况是怎样的?
典例精析
例1 一商店在某一时间以每件 60 元的价格卖出两件衣服,其中一件盈利 25% ,另一件亏损 25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
¥60
¥60
思考:销售的盈亏决定于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价 > 总成本
总售价 < 总成本
总售价 = 总成本
盈 利
亏 损
不盈不亏
(2) 设亏损 25% 的衣服进价是 y 元,
依题意得 y-0.25y = 60
解得 y = 80
(1) 设盈利 25% 的衣服进价是 x 元,
依题意得 x+0.25 x = 60
解得 x = 48
解:
两件衣服总成本:x+y = 48+80 =128(元)
因为 120-128 = -8(元)
所以卖这两件衣服共亏损了 8 元.
与你猜想的一致吗?
1. 某琴行同时卖出两台钢琴,每台售价为 960 元.其中一台盈利 20%,另一台亏损 20%.这次琴行是盈利还是亏损,或是不盈不亏?
练一练
2. 某文具店有两个进价不同的计算器都卖 64 元,其中一个盈利 60%,另一个亏本 20%.这次交易中的盈亏情况?
答案:买这两个计算器盈利 8 元.
答案:这次琴行亏本 80 元.
例2 一件服装先将进价提高 25% 出售,后进行促销活动,又按标价的 8 折出售,此时售价为 60 元. 请问商家是盈是亏,还是不盈不亏?
解:设这件衣服的进价是 x 元,
则提价后的售价是 (1+25%)x 元,
促销后的售价是 (1+25%)x×0.8 元,
依题意得 (1+25%)x×0.8 = 60
解得 x = 60
售价 60 = 成本 60 答:这家商店不盈不亏.
练一练
1. 某商品在原价的基础上提高 25% 标价,若想调回原价,应降价的百分率为 .
20%
2. 我国政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品在 2021 年涨价 30% 后,2023 年降价 70% 至 a 元,则这种药品在 2005 年涨价前价格为 元.
1. 某商品的进价是 1000 元,售价是 1500 元,由于销售情况不好,商店决定降价出售,但又要保证利润率不低于 5%,那么商店最多可打几折出售此商品?
解:设商店最多可以打 x 折出售此商品,
根据题意,得
1500× = 1000(1+5%)
解得 x = 7
答:商店最多可以打 7 折出售此商品.
2. 据了解个体商店销售中售价只要高出进价的 20% 便可盈利,但老板们常以高出进价 50% ~ 100% 标价,假若你准备买一双标价为 600 元的运动鞋,应在什么范围内还价?
高于进价 50% 标价 高于进价 100% 标价
进价 x 元 y 元
标价 (1+50%)x (1+100%)y
方程 (1+50%)x = 600 (1+100%)y = 600
方程的解 x = 400 y = 300
盈利价 400(1+20%) = 480 300(1+20%) = 360
答:应在 480 元 ~ 360 元内还价.
商品利润
利润率 =
= 商品售价-商品进价
●售价、进价、利润的关系:
商品利润
●进价、利润、利润率的关系:
商品进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价 =
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价 =
×(1 + 利润率)
打
折
销
售
6.3 实践与探索
第 3 课时 速率问题
华东师大版数学七年级下册
情境引入
你知道它蕴含的是我们数学中的什么问题吗?
相遇问题
星期天早晨,小斌和小强分别骑自行车从家里同时出发去参观雷锋纪念馆. 已知他俩的家到雷锋纪念馆的路程相等,小斌每小时骑 10 km,他在上午 10 时到达;小强每时骑 15 km,他在上午 9 时 30 分到达.求他们的家到雷锋纪念馆的路程.
情境引入
由于小斌的速度较慢,因此他花的时间比小强花的时间多.
本问题中涉及的等量关系有:
.
因此,设他俩的家到雷锋纪念馆的路程均为 s km,
解得 s = ____.
因此,小斌和小强的家到雷锋纪念馆的路程为 km.
根据等量关系,得
.
15
15
注意单位要统一.
例1 小明与小红的家相距 20 km,小明从家里出发骑自行车去小红家,两人商定小红到时候从家里出发骑自行车去接小明. 已知小明骑车的速度为 13 km/h,小红骑车的速度是 12 km/h.
(1) 如果两人同时出发,那么他们经过多少小时相遇?
分析:由于小明与小红都从家里出发,相向而行,所以相遇时,他们走的路程的和等于两家之间的距离.即
小明走的路程+小红走的路程 = 两家之间的距离(20 km).
典例精析
解:设小明与小红骑车走了 x h 后相遇,
则根据等量关系,得
13x + 12x = 20 .
解得 x = 0.8 .
答:经过 0.8 h 他们两人相遇.
小明走的路程
小红走的路程
(2) 如果小明先走 30 min,那么小红骑车要走多少小时才能与小明相遇?
小明先走的路程
小红出发后小明走的路程
小红走的路程
解:设小红骑车走了 t h 后与小明相遇,
则根据等量关系,得
13(0.5 + t )+12t = 20 .
解得 t = 0.54 .
答:小红骑车走 0.54 h 后与小明相遇.
路程=速度×时间
甲走的路程+乙走的路程=甲、乙之间的距离
相遇问题
总结归纳
注意相向而行的始发时间和地点.
甲、乙两车分别从 A,B 两地同时出发,相向而行.已知 A,B 两地的距离为 480 km,且甲车以 65 km/ h 的速度行驶.若两车 4 h 后相遇,则乙车的行驶速度是多少?
答:乙车的行驶速度是 55 km/h.
练一练
例2 小明早晨要在 7:20 以前赶到距家 1000 米的学校上学.一天,小明以 80 米/分钟的速度出发,5 分钟后,小明的爸爸发现他忘了带历史作业,于是,爸爸立即以 180 米/分钟的速度去追小明,并且在途中追上了他.
问爸爸追上小明用了多长时间?
分析:当爸爸追上小明时,两人所走路程相等.
追及问题
解:设爸爸追上小明用了 x 分钟,则此题的数量关系可用线段图表示.
据题意,得 80×5+80x = 180x.
答:爸爸追上小明用了 4 分钟.
解得 x = 4.
80×5
80x
180x
一队学生步行去郊外春游,每小时走 4 km,学生甲因故推迟出发 30 min,为了赶上队伍,甲以 6 km/h的速度追赶,问甲用多少时间就可追上队伍?
答:该生用了 1 小时追上了队伍.
练一练
路程 = 速度×时间
S快-S慢 = S原来距离
追及问题
总结归纳
注意同向而行始发时间和地点.
例3 生产的这批螺钉、螺母要打包,由一个人做要 40 h 完成.现计划由一部分人先做 4 h,然后增加 2 人与他们一起做 8 h,完成这项工作. 假设这些人的工作效率相同,具体应该安排多少人工作?
分析:
人均效率 人数 时间 工作量
前一部分工作 x 4
后一部分工作 x+2 8
×
=
×
工作量之和等于总工作量 1 .
工程问题
×
×
=
解:设先安排 x 人做 4 h,根据题意得等量关系:
可列方程
解方程,得 4x+8(x+2)=40,
4x+8x+16=40,
12x = 24,
x = 2.
答:应先安排 2人做 4 小时.
前部分工作总量+后部分工作总量=总工作量 1
一条地下管线由甲工程队单独铺设需要 12 天,由乙工程队单独铺设需要 24 天. 如果由这两个工程队从两端同时施工,要多少天可以铺好这条管线?
做一做
根据工作效率×工作时间 = 工作量,列方程:
解:设要 x 天可以铺好这条管线,由题意得
答:要 8 天可以铺好这条管线.
分析:把工作量看作单位“1”,则甲的工作效率为 ,乙的工作效率为 .
解方程,得
解决工程问题的思路:
1. 三个基本量:
三个基本量:工作量、工作效率、工作时间.
工作量=工作效率×工作时间.
若把工作量看作 1 ,则工作效率 =
2. 相等关系:
(1) 按工作时间,各时间段的工作量之和 = 完成的工作量.
(2) 按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量 = 完成的工作量.
要点归纳
1.甲每小时走 5 千米,甲出发 4.5 小时后,乙骑车从同一地点出发追赶甲,乙用了 35 分钟追上甲,设乙骑车的速度为 x 千米/时,则所列方程为( )
B
2.甲、乙两人骑摩托车同时从相距 170 千米的 A,B 两地相向而行,2 小时相遇,如果甲比乙每小时多行 5 千米,则乙每小时行( )
A.30千米 B.40千米 C.50千米 D.45千米
B
3.甲、乙两人在 400 米的环形跑道上练习长跑,他们同时同地反向而跑,甲的速度是 6 米/秒,乙的速度是 4 米/秒,则他们首次相遇时,两人都跑了( )
A.40秒 B.50秒 C.60秒 D.70秒
A
4. 一项工作,甲独做需 18 天,乙独做需 24 天,如果两人合做 8 天后,余下的工作再由甲独做 x 天完成,
那么所列方程为____________.
行程问题
路程=速度×时间
相遇问题
追及问题
甲走的路程+乙走的路程 =甲、乙之间的距离
S快-S慢= S原来距离
解决工程问题的思路:
1. 三个基本量:
三个基本量:工作量、工作效率、工作时间.
工作量=工作效率×工作时间.
若把工作量看作 1 ,则工作效率 =
2. 相等关系:
(1) 按工作时间,各时间段的工作量之和 = 完成的工作量.
(2) 按工作者,若一项工作有甲、乙两人参与,则甲的工作量+乙的工作量 = 完成的工作量.
谢谢观看
华东师大版数学七年级下册
