2023-2024学年华师版数学七年级下册 9.1 三角形 教案(2课时)
文档属性
| 名称 | 2023-2024学年华师版数学七年级下册 9.1 三角形 教案(2课时) |

|
|
| 格式 | docx | ||
| 文件大小 | 881.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 00:00:00 | ||
图片预览


文档简介
第9章 多边形
9.1 三角形
9.1.1 认识三角形
第1课时 三角形的有关概念
1.理解三角形的概念.
2.认识三角形的顶点、边、角,外角,会数三角形的个数.(重点)
3. 掌握三角形的两种分类方法.
一、情境导入
出示金字塔、战机、大桥等图片,让学生感受生活中的三角形,体会生活中处处有数学.
教师利用多媒体演示三角形的形成过程,让学生观察.
问:你能不能给三角形下一个完整的定义?
二、合作探究
探究点一:三角形的概念
下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
解析:根据三角形的定义为:由不在同一条直线上的三条线段首尾顺次相接所成的图形来解答.故选D.
方法总结:解题的关键是熟练记住并理解三角形的定义.
如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
解析:根据题意画出图形即可得到结论.
解:如图所示,以A,B为顶点,得△ABC,△ADB,△ABE,
以A,C为顶点,得△ACD,△ACE,
以A,D为顶点,得△ADE,以B,C为顶点,得△BCE,△BCD,
以B,D为顶点,得△BDE,以C,D为顶点,得△CDE,
故以其中任意三个点为顶点画三角形,最多可以画10个三角形,
故答案为:10.
方法总结:正确画出所有的三角形是关键.
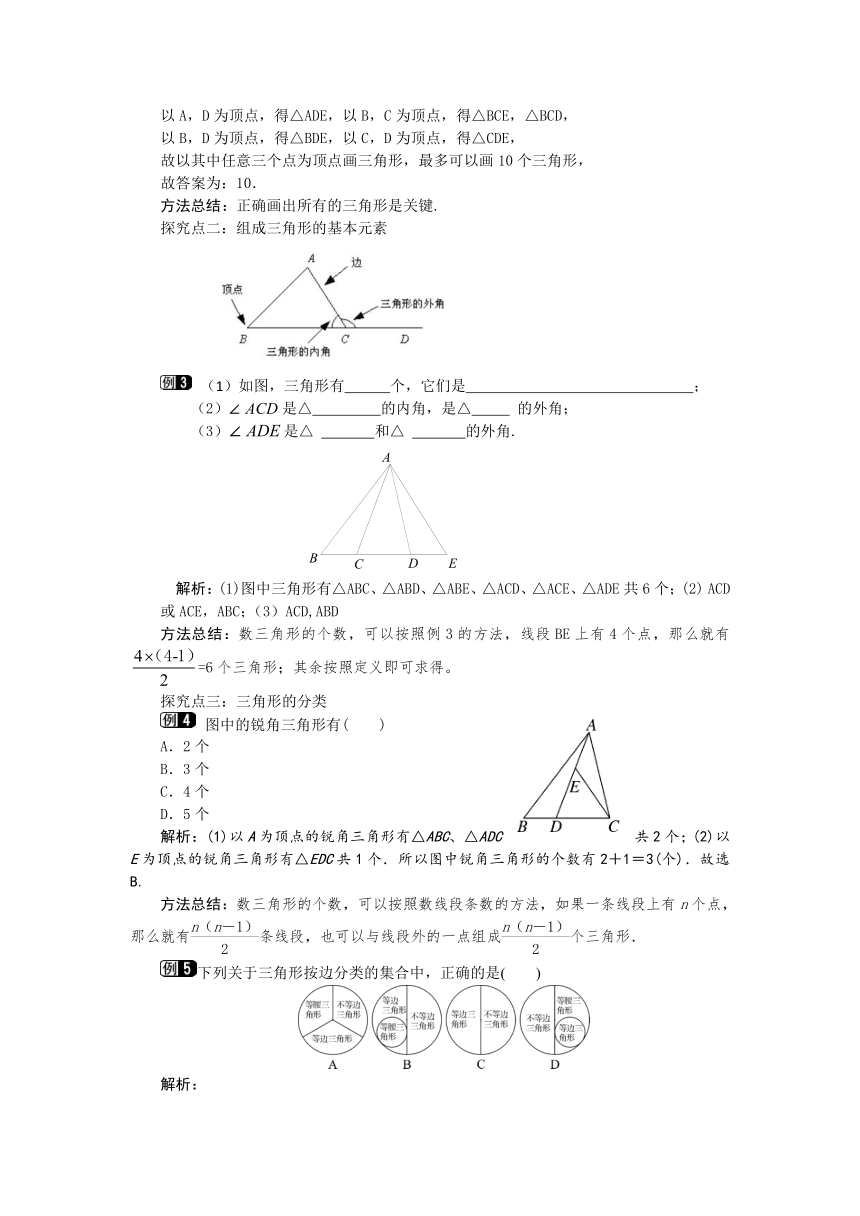
探究点二:组成三角形的基本元素
(1)如图,三角形有 个,它们是 ;
(2)是△ 的内角,是△ 的外角;
(3)是△ 和△ 的外角.
解析:(1)图中三角形有△ABC、△ABD、△ABE、△ACD、△ACE、△ADE共6个;(2) ACD或ACE,ABC;(3)ACD,ABD
方法总结:数三角形的个数,可以按照例3的方法,线段BE上有4个点,那么就有=6个三角形;其余按照定义即可求得。
探究点三:三角形的分类
图中的锐角三角形有( )
A.2个
B.3个
C.4个
D.5个
解析:(1)以A为顶点的锐角三角形有△ABC、△ADC共2个;(2)以E为顶点的锐角三角形有△EDC共1个.所以图中锐角三角形的个数有2+1=3(个).故选B.
方法总结:数三角形的个数,可以按照数线段条数的方法,如果一条线段上有n个点,那么就有条线段,也可以与线段外的一点组成个三角形.
下列关于三角形按边分类的集合中,正确的是( )
解析:
故选D.
方法总结:三角形按边分类,分成不等边三角形与等腰三角形,知道等边三角形是特殊的等腰三角形是解本题的关键.
三、板书设计
认识三角形
1.三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形.
2.组成三角形的基本元素:
3.三角形外角的定义:三角形的一边与另一边的延长线组成的角.
4.三角形的两种分类方法:
(1)按角分为:锐角三角形,直角三角形,钝角三角形;
(2)按边分为:
本节课让学生经历一个探究认识三角形的过程,从实际生活中抽象出三角形,进一步探究这些图形的组成元素及分类方法,这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
9.1.1 认识三角形
第2课时 三角形中的重要线段
1.掌握三角形的高、中线和角平分线的定义,并能够对其进行简单的应用.(重点)
2.能够准确的画出三角形的高、中线和角平分线.(难点)
情境导入
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?本节我们一起来解决这个问题.
二、合作探究
探究点一:三角形的高
【类型一】 三角形高的画法
画△ABC的边AB上的高,下列画法中,正确的是( )
解析:三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.根据概念可知.
解:过点C作边AB的垂线段,即画AB边上的高CD,所以画法正确的是D.故选D.
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
【类型二】 根据三角形的面积求高
如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
解析:根据垂线段最短,可知当BP⊥AC时,BP有最小值.由△ABC的面积公式可知AD·BC=BP·AC,解得BP=.
方法总结:解答此题可利用面积相等作桥梁(但不求面积)求三角形的高,这种解题方法通常称为“等面积法”.
探究点二:三角形的中线
【类型一】 应用三角形的中线求线段的长
在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
解析:如图,∵AD是△ABC的中线,∴BD=CD,∴△ABD的周长-△ADC的周长=(BA+BD+AD)-(AC+AD+CD)=BA-AC,∴BA-5=2,∴BA=7cm.
方法总结:通过本题要理解三角形的中线的定义,解决问题的关键是将△ABD与△ADC的周长之差转化为边长的差.
【类型二】 利用中线解决三角形的面积问题
如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,
△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
解析:∵点D是AC的中点,∴AD=AC.∵S△ABC=12,∴S△ABD=S△ABC=×12=6.∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.故答案为2.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
探究点三:三角形的角平分线
如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( ).
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A. 4个 B.3个 C.2个 D.1个
解析:由∠1=∠2,根据三角形的角平分线的定义得出AE平分∠DAF,故③正确;又
∠3=∠4,利用等式的性质得到∠1+∠3=∠2+∠4,即∠BAE=∠EAC,那么AE平分∠BAC,故⑤正确.故选:C.
方法总结:三角形的角平分线的定义
三、板书设计
三角形的高、中线与角平分线
1.三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
3.三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点与交点的线段叫做三角形的角平分线.
本节课由实际问题“平分三角形蛋糕”引入,让学生意识到数学与实际生活的密切联系,明确数学来源于实践应用于实践,进而学习用数学方法解决实际问题.然后从画图入手,分三种情况:即锐角三角形、直角三角形和钝角三角形,培养学生形成分类讨论思想,同时,可以在学生头脑中对这三种线段留下清晰的形象,然后结合这些具体形象叙述它们的定义以及表示方法,最后通过例题进一步巩固.
9.1 三角形
9.1.1 认识三角形
第1课时 三角形的有关概念
1.理解三角形的概念.
2.认识三角形的顶点、边、角,外角,会数三角形的个数.(重点)
3. 掌握三角形的两种分类方法.
一、情境导入
出示金字塔、战机、大桥等图片,让学生感受生活中的三角形,体会生活中处处有数学.
教师利用多媒体演示三角形的形成过程,让学生观察.
问:你能不能给三角形下一个完整的定义?
二、合作探究
探究点一:三角形的概念
下面是一位同学用三根木棒拼成的图形,其中符合三角形概念的是( )
解析:根据三角形的定义为:由不在同一条直线上的三条线段首尾顺次相接所成的图形来解答.故选D.
方法总结:解题的关键是熟练记住并理解三角形的定义.
如图,平面内有五个点,以其中任意三个点为顶点画三角形,最多可以画 个三角形.
解析:根据题意画出图形即可得到结论.
解:如图所示,以A,B为顶点,得△ABC,△ADB,△ABE,
以A,C为顶点,得△ACD,△ACE,
以A,D为顶点,得△ADE,以B,C为顶点,得△BCE,△BCD,
以B,D为顶点,得△BDE,以C,D为顶点,得△CDE,
故以其中任意三个点为顶点画三角形,最多可以画10个三角形,
故答案为:10.
方法总结:正确画出所有的三角形是关键.
探究点二:组成三角形的基本元素
(1)如图,三角形有 个,它们是 ;
(2)是△ 的内角,是△ 的外角;
(3)是△ 和△ 的外角.
解析:(1)图中三角形有△ABC、△ABD、△ABE、△ACD、△ACE、△ADE共6个;(2) ACD或ACE,ABC;(3)ACD,ABD
方法总结:数三角形的个数,可以按照例3的方法,线段BE上有4个点,那么就有=6个三角形;其余按照定义即可求得。
探究点三:三角形的分类
图中的锐角三角形有( )
A.2个
B.3个
C.4个
D.5个
解析:(1)以A为顶点的锐角三角形有△ABC、△ADC共2个;(2)以E为顶点的锐角三角形有△EDC共1个.所以图中锐角三角形的个数有2+1=3(个).故选B.
方法总结:数三角形的个数,可以按照数线段条数的方法,如果一条线段上有n个点,那么就有条线段,也可以与线段外的一点组成个三角形.
下列关于三角形按边分类的集合中,正确的是( )
解析:
故选D.
方法总结:三角形按边分类,分成不等边三角形与等腰三角形,知道等边三角形是特殊的等腰三角形是解本题的关键.
三、板书设计
认识三角形
1.三角形的概念:
由不在同一直线上的三条线段首尾顺次相接所组成的图形.
2.组成三角形的基本元素:
3.三角形外角的定义:三角形的一边与另一边的延长线组成的角.
4.三角形的两种分类方法:
(1)按角分为:锐角三角形,直角三角形,钝角三角形;
(2)按边分为:
本节课让学生经历一个探究认识三角形的过程,从实际生活中抽象出三角形,进一步探究这些图形的组成元素及分类方法,这样教学符合学生的认知特点,既提高了学生学习的兴趣,又增强了学生的动手能力.
9.1.1 认识三角形
第2课时 三角形中的重要线段
1.掌握三角形的高、中线和角平分线的定义,并能够对其进行简单的应用.(重点)
2.能够准确的画出三角形的高、中线和角平分线.(难点)
情境导入
这里有一块三角形的蛋糕,如果兄弟两个想要平分的话,你该怎么办呢?本节我们一起来解决这个问题.
二、合作探究
探究点一:三角形的高
【类型一】 三角形高的画法
画△ABC的边AB上的高,下列画法中,正确的是( )
解析:三角形的高即从三角形的顶点向对边引垂线,顶点和垂足间的线段.根据概念可知.
解:过点C作边AB的垂线段,即画AB边上的高CD,所以画法正确的是D.故选D.
方法总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
【类型二】 根据三角形的面积求高
如图所示,在△ABC中,AB=AC=5,BC=6,AD⊥BC于点D,且AD=4,若点P在边AC上移动,则BP的最小值为________.
解析:根据垂线段最短,可知当BP⊥AC时,BP有最小值.由△ABC的面积公式可知AD·BC=BP·AC,解得BP=.
方法总结:解答此题可利用面积相等作桥梁(但不求面积)求三角形的高,这种解题方法通常称为“等面积法”.
探究点二:三角形的中线
【类型一】 应用三角形的中线求线段的长
在△ABC中,AC=5cm,AD是△ABC的中线,若△ABD的周长比△ADC的周长大2cm,则BA=________.
解析:如图,∵AD是△ABC的中线,∴BD=CD,∴△ABD的周长-△ADC的周长=(BA+BD+AD)-(AC+AD+CD)=BA-AC,∴BA-5=2,∴BA=7cm.
方法总结:通过本题要理解三角形的中线的定义,解决问题的关键是将△ABD与△ADC的周长之差转化为边长的差.
【类型二】 利用中线解决三角形的面积问题
如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,
△ADF和△BEF的面积分别为S△ABC,S△ADF和S△BEF,且S△ABC=12,则S△ADF-S△BEF=________.
解析:∵点D是AC的中点,∴AD=AC.∵S△ABC=12,∴S△ABD=S△ABC=×12=6.∵EC=2BE,S△ABC=12,∴S△ABE=S△ABC=×12=4.∵S△ABD-S△ABE=(S△ADF+S△ABF)-(S△ABF+S△BEF)=S△ADF-S△BEF,即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2.故答案为2.
方法总结:三角形的中线将三角形分成面积相等的两部分;高相等时,面积的比等于底边的比;底相等时,面积的比等于高的比.
探究点三:三角形的角平分线
如图所示,∠1=∠2,∠3=∠4,则下列结论正确的有( ).
①AD平分∠BAF;②AF平分∠BAC;③AE平分∠DAF;④AF平分∠DAC;⑤AE平分∠BAC.
A. 4个 B.3个 C.2个 D.1个
解析:由∠1=∠2,根据三角形的角平分线的定义得出AE平分∠DAF,故③正确;又
∠3=∠4,利用等式的性质得到∠1+∠3=∠2+∠4,即∠BAE=∠EAC,那么AE平分∠BAC,故⑤正确.故选:C.
方法总结:三角形的角平分线的定义
三、板书设计
三角形的高、中线与角平分线
1.三角形的高:从三角形的一个顶点向它的对边作垂线,顶点和垂足间的线段叫做三角形的高.
2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.
3.三角形的角平分线:三角形的一个角的平分线与这个角的对边相交,连接这个角的顶点与交点的线段叫做三角形的角平分线.
本节课由实际问题“平分三角形蛋糕”引入,让学生意识到数学与实际生活的密切联系,明确数学来源于实践应用于实践,进而学习用数学方法解决实际问题.然后从画图入手,分三种情况:即锐角三角形、直角三角形和钝角三角形,培养学生形成分类讨论思想,同时,可以在学生头脑中对这三种线段留下清晰的形象,然后结合这些具体形象叙述它们的定义以及表示方法,最后通过例题进一步巩固.
