8.1.3 同底数幂的除法 课件(共43张PPT) 2023-2024学年沪科版数学七年级下册
文档属性
| 名称 | 8.1.3 同底数幂的除法 课件(共43张PPT) 2023-2024学年沪科版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 00:00:00 | ||
图片预览





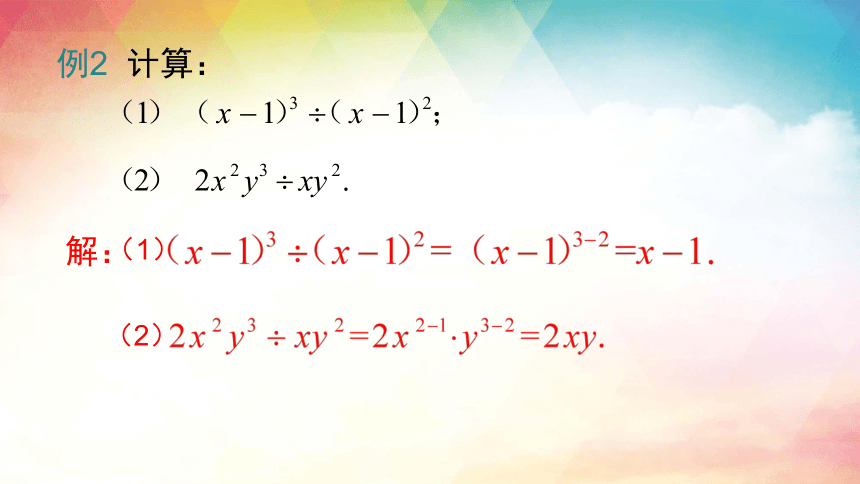


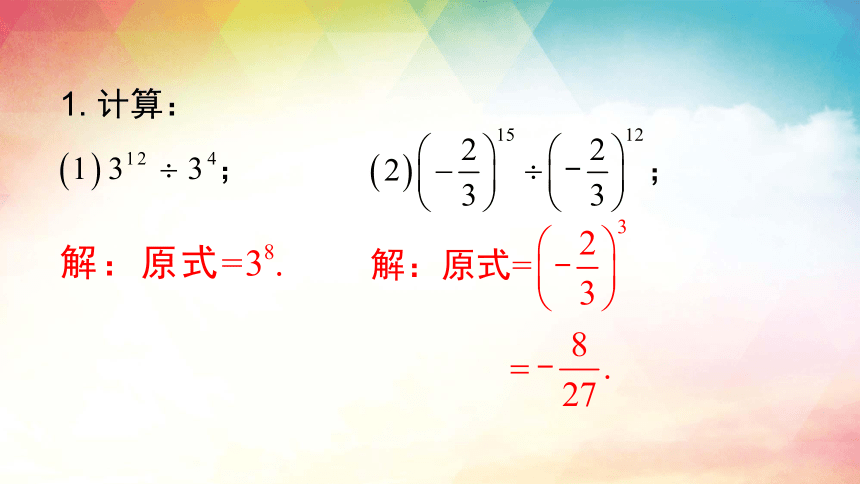

文档简介
(共43张PPT)
第8章 整式乘法与因式分解
8.1 幂的运算
第1课时 同底数幂的除法
3.同底数幂的除法
沪科版数学七年级下册
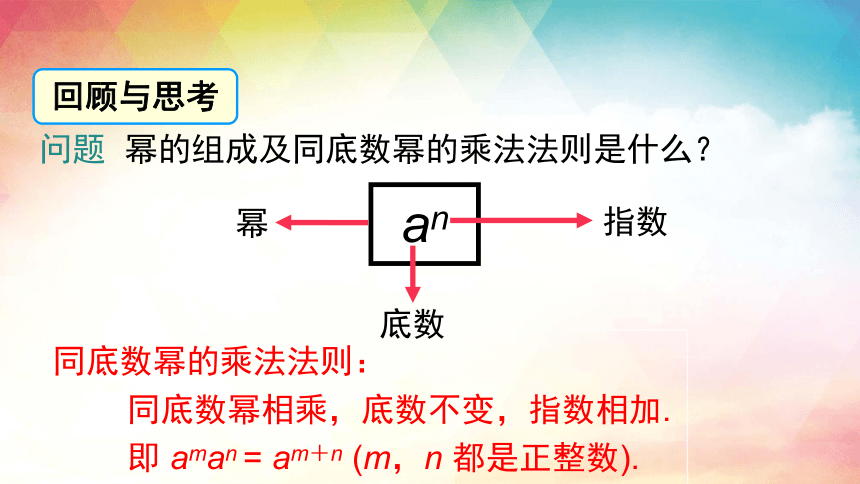
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即 aman = am+n (m,n 都是正整数).
回顾与思考
an
底数
幂
指数
情境导入
一种液体每升含有 1012 个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现 1 滴杀菌剂可以杀死 109 个此种细菌.要将 1 升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109.
(2) 观察这个算式,它有何特点?
我们观察可以发现,1012 和 109 这两个幂的底数相同,
是同底数的幂的形式. 所以我们把 1012÷109 这种运算叫做同底数幂的除法.
(1) 怎样列式?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )×27=215
( )×53= 55
( )×a5=a7
( )×3n=3m
28
a2
52
乘法与除法互为逆运算
215÷27 = ( )
= 215-7
55÷53 = ( )
= 55-3
a7÷a5 = ( )
= a7-5
3m÷3n = ( )
3m-n
28
52
a2
填一填:
通过上述运算你发现了什么规律?
自主探究
3m-n
同底数幂的除法
猜想:am÷an = am-n (m>n).
验证:am÷an =
m 个 a
n 个 a
= (a · a · ··· · a)
(m-n) 个 a
= am-n.
总结归纳
( a≠0,m,n 是正整数,且 m>n ).
am÷an = am-n
即:同底数幂相除,底数不变,指数相减.
例1 计算:
典例精析
解:
例2 计算:
解:
(1)
(2)
例3 已知:am = 3,an = 5. 求:
(1) am-n 的值; (2) a3m-3n 的值.
解:(1) am-n = am÷an = 3÷5 = 0.6.
(2) a3m-3n = a3m÷a3n
= (am)3÷(an)3
= 33÷53 = 27÷125
=
同底数幂的除法可以逆用:am-n = am÷an.
这种思维叫做逆向思维 (逆用运算性质).
例4 如果地球的体积大约是 1×1012 千米3,太阳的体积大约为 1.5×1018 千米3,请问太阳的体积是地球体积的多少倍?
18个10
12个10
6个10
同底数幂的除法的实际应用
1. 计算:
2. 下面的计算对不对?如果不对,请改正.
3. 已知 3m = 2,9n = 10,求 33m-2n 的值.
解:33m-2n = 33m÷32n
= (3m)3÷(32)n
= (3m)3÷9n
= 23÷10
= 8÷10
= 0.8.
4. 地震的强度通常用里克特震级表示,描绘地震级的数字表示地震的强度是 10 的若干次幂. 例如,用里克特震级表示地震是 8 级,说明地震的强度是 107. 1992 年 4 月,荷兰发生了 5 级地震,12 天后,加利福尼亚发生了 7 级地震,加利福尼亚的地震强度是荷兰地震强度的多少倍?
解:由题意得 .
答:加利福尼亚的地震强度是荷兰地震强度的 100 倍.
同底数幂的除法
法则
am÷an = am-n (a ≠ 0,m,n 都是正整数,且 m>n)
同底数幂相除,底数不变,指数相减
同底数幂的除法法则的逆用:
am-n = am÷an (a ≠ 0,m,n 都是正整数,且 m>n)
第8章 整式乘法与因式分解
8.1 幂的运算
第2课时 零次幂、负整数次幂及科学记数法
3.同底数幂的除法
沪科版数学七年级下册
同底数幂相除,底数不变,指数相减.
即
问题 同底数幂的除法法则是什么?
回顾与思考
若 m≤n,同底数幂的除法怎么计算呢?该法则还适用吗?
根据除法法则,如果 a ≠ 0,m 是正整数,那么 am÷am 等于多少?
am÷am = 1.
问题引导
零次幂
如果把公式 am÷an = am-n (a ≠ 0,m,n 都是正整数,且 m>n) 推广到 m = n 的情形,那么就会有
am÷an = am-m = a0.
这启发我们规定
即任何不等于零的数的零次幂都等于 1.
总结归纳
想一想:为何 a 不能等于 0 呢?
例1 已知 (3x - 2)0 有意义,则 x 应满足的条件是_______.
解析:根据零次幂的意义可知:若 (3x-2)0 有意义,则 3x - 2 ≠ 0.
方法总结:零次幂有意义的条件是底数不等于 0,所以解决有关零次幂的意义问题时,可列出关于底数不等于 0 的式子求解即可.
典例精析
例2 若 (x - 1)x+1 = 1,求 x 的值.
解:①当 x+1 = 0,即 x = -1 时,(x - 1)x+1 = (-2)0 = 1;
②当 x - 1 = 1,即 x = 2 时,(x - 1)x+1 = 13 = 1;
③当 x - 1 = -1,即 x = 0 时,(x - 1)x+1 = (-1)1 = -1.
故 x 的值为 -1 或 2.
方法总结:乘方的结果为 1,可分为三种情况:不为零的数的零次幂等于 1;1 的任何次幂都等于 1;-1 的偶次幂等于 1. 即在底数不等于 0 的情况下要考虑指数等于 0,另外还需考虑底数等于 1 或-1 的情况.
问题:计算:a3÷a5 (a ≠ 0).
解法1
解法2 假如把正整数指数幂的除法法则 am÷an = am-n
(a ≠ 0,m,n 是正整数,m>n) 中的 m>n 这个条件去掉,那么 a3÷a5 = a3-5 = a-2.
于是得到:
负整数指数幂
特别地,
总结归纳
如果令公式 am÷an = am-n 中的 m = 0,那么就会有
例3 计算:
解:
典例精析
例4 若 a = ,b = (-1)-1,c = ,则 a,b,c 的大小关系是( )
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
B
解析:a = = = ,b = (-1)-1 = -1,c =
= 1,故 a>c>b.
方法总结:关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
例5 把下列各数写成分数的形式:
解:
例6 计算:
解析:分别根据有理数的乘方、零指数幂、负整数指数幂及绝对值的性质计算出各数,再根据实数的运算法则进行计算.
科学记数法:绝对值大于 10 的数记成 a×10n 的形式,其中 1≤|a|<10,n 是正整数.
忆一忆:
例如,864000 可以写成 .
怎样用科学记数法表示 0.0000864?
8.64×105
想一想:
用科学计数法表示绝对值小于 1 的数
探一探:
因为
所以,0.0000864 = 8.64×0.00001 = 8.64 ×10-5.
类似地,我们可以利用 10 的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.
算一算:
10-2 = ___________; 10-4 = ___________;
10-8 = ___________.
议一议:指数与运算结果的 0 的个数有什么关系?
一般地,10 的 -n 次幂,在 1 前面有_____个 0.
想一想:10-21 的小数点后的位数是几位?
1 前面有几个零?
0.01
0.0001
0.00000001
通过上面的探索,你发现了什么?
n
用科学记数法表示一些绝对值小于 1 的数的方法:
利用 10 的负整数次幂,把一个绝对值小于 1 的数表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.
n 等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面那个零).
知识要点
例7 用小数表示下列各数:
(1) 2×10-7; (2) 3.14×10-5;
(3) 7.08×10-3; (4) 2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1) 2×10-7=0.0000002.
(2) 3.14×10-5=0.0000314.
(3) 7.08×10-3=0.00708.
(4) 2.17×10-1=0.217.
1. 用科学记数法表示:
(1)0.000 03; (2)-0.000 006 4;
(3)0.000 0314.
2. 用科学记数法填空:
(1)1 s 是 1 μs 的 1 000 000 倍,则 1 μs=_______s;
(2)1 mg=_______kg; (3)1 μm=_______m;
(4)1 nm=_______μm; (5)1 cm2=_______ m2;
(6)1 mL=_______m3.
练一练
3×10-5
3.14×10-5
-6.4×10-6
1×10-6
1×10-6
1×10-6
1×10-3
1×10-4
1×10-6
3. 中国女药学家屠呦呦获 2015 年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下某种疟原虫平均长度为 0.0000015 米,该长度用科学记数法表示为__________米.
1.5×10-6
1. 计算:
1
1
64
2. 把下列各数写成分数的形式:
3. 用小数表示 5.6×10-4.
解:原式 = 5.6×0.0001 = 0.00056.
4. 比较大小:
(1)3.01×10-4_______9.5×10-3;
(2)3.01×10-4_______3.10×10-4.
<
<
5. 用科学记数法把小数 0.000 009 405 表示成
9.405×10n 的形式,那么 n = .
-6
6.计算:-32+(- )-2+(2023+π)0-|2- π|.
=-9+9+1-2+ π
= π-1.
解:-32+(- )-2+(2023+π)0-|2- π|
7. 随着微电子制造技术的不断进步,半导体材料的精加工尺寸大幅度缩小,目前已经能够在 350 平方毫米的芯片上集成 5 亿个元件,问 1 个这样的元件大约占多少平方毫米?
解析:因为 350 平方毫米的芯片上集成 5 亿个元件,说明 5 亿个元件所占的面积为 350 平方毫米,要计算 1 个元件所占的面积,可用 350 除以 5 亿.
注意:用科学记数法表示实际生活中的数量时,不能漏掉单位.
整数指数幂
非正整数
指数幂的意义
1. 零指数幂:当 a ≠ 0 时,a0 = 1
2. 负整数指数幂:当 n 是正整数时,a-n=
科学记数法表示绝对值较小的数
0.00…01
n 个 0
谢谢观看
沪科版数学七年级下册
第8章 整式乘法与因式分解
8.1 幂的运算
第1课时 同底数幂的除法
3.同底数幂的除法
沪科版数学七年级下册
问题 幂的组成及同底数幂的乘法法则是什么?
同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
即 aman = am+n (m,n 都是正整数).
回顾与思考
an
底数
幂
指数
情境导入
一种液体每升含有 1012 个有害细菌,为了试验某种杀菌剂的效果,科学家们进行了实验,发现 1 滴杀菌剂可以杀死 109 个此种细菌.要将 1 升液体中的有害细菌全部杀死,需要这种杀菌剂多少滴?
1012÷109.
(2) 观察这个算式,它有何特点?
我们观察可以发现,1012 和 109 这两个幂的底数相同,
是同底数的幂的形式. 所以我们把 1012÷109 这种运算叫做同底数幂的除法.
(1) 怎样列式?
根据同底数幂的乘法法则进行计算:
28×27= 52×53=
a2×a5= 3m-n×3n=
215
55
a7
3m
( )×27=215
( )×53= 55
( )×a5=a7
( )×3n=3m
28
a2
52
乘法与除法互为逆运算
215÷27 = ( )
= 215-7
55÷53 = ( )
= 55-3
a7÷a5 = ( )
= a7-5
3m÷3n = ( )
3m-n
28
52
a2
填一填:
通过上述运算你发现了什么规律?
自主探究
3m-n
同底数幂的除法
猜想:am÷an = am-n (m>n).
验证:am÷an =
m 个 a
n 个 a
= (a · a · ··· · a)
(m-n) 个 a
= am-n.
总结归纳
( a≠0,m,n 是正整数,且 m>n ).
am÷an = am-n
即:同底数幂相除,底数不变,指数相减.
例1 计算:
典例精析
解:
例2 计算:
解:
(1)
(2)
例3 已知:am = 3,an = 5. 求:
(1) am-n 的值; (2) a3m-3n 的值.
解:(1) am-n = am÷an = 3÷5 = 0.6.
(2) a3m-3n = a3m÷a3n
= (am)3÷(an)3
= 33÷53 = 27÷125
=
同底数幂的除法可以逆用:am-n = am÷an.
这种思维叫做逆向思维 (逆用运算性质).
例4 如果地球的体积大约是 1×1012 千米3,太阳的体积大约为 1.5×1018 千米3,请问太阳的体积是地球体积的多少倍?
18个10
12个10
6个10
同底数幂的除法的实际应用
1. 计算:
2. 下面的计算对不对?如果不对,请改正.
3. 已知 3m = 2,9n = 10,求 33m-2n 的值.
解:33m-2n = 33m÷32n
= (3m)3÷(32)n
= (3m)3÷9n
= 23÷10
= 8÷10
= 0.8.
4. 地震的强度通常用里克特震级表示,描绘地震级的数字表示地震的强度是 10 的若干次幂. 例如,用里克特震级表示地震是 8 级,说明地震的强度是 107. 1992 年 4 月,荷兰发生了 5 级地震,12 天后,加利福尼亚发生了 7 级地震,加利福尼亚的地震强度是荷兰地震强度的多少倍?
解:由题意得 .
答:加利福尼亚的地震强度是荷兰地震强度的 100 倍.
同底数幂的除法
法则
am÷an = am-n (a ≠ 0,m,n 都是正整数,且 m>n)
同底数幂相除,底数不变,指数相减
同底数幂的除法法则的逆用:
am-n = am÷an (a ≠ 0,m,n 都是正整数,且 m>n)
第8章 整式乘法与因式分解
8.1 幂的运算
第2课时 零次幂、负整数次幂及科学记数法
3.同底数幂的除法
沪科版数学七年级下册
同底数幂相除,底数不变,指数相减.
即
问题 同底数幂的除法法则是什么?
回顾与思考
若 m≤n,同底数幂的除法怎么计算呢?该法则还适用吗?
根据除法法则,如果 a ≠ 0,m 是正整数,那么 am÷am 等于多少?
am÷am = 1.
问题引导
零次幂
如果把公式 am÷an = am-n (a ≠ 0,m,n 都是正整数,且 m>n) 推广到 m = n 的情形,那么就会有
am÷an = am-m = a0.
这启发我们规定
即任何不等于零的数的零次幂都等于 1.
总结归纳
想一想:为何 a 不能等于 0 呢?
例1 已知 (3x - 2)0 有意义,则 x 应满足的条件是_______.
解析:根据零次幂的意义可知:若 (3x-2)0 有意义,则 3x - 2 ≠ 0.
方法总结:零次幂有意义的条件是底数不等于 0,所以解决有关零次幂的意义问题时,可列出关于底数不等于 0 的式子求解即可.
典例精析
例2 若 (x - 1)x+1 = 1,求 x 的值.
解:①当 x+1 = 0,即 x = -1 时,(x - 1)x+1 = (-2)0 = 1;
②当 x - 1 = 1,即 x = 2 时,(x - 1)x+1 = 13 = 1;
③当 x - 1 = -1,即 x = 0 时,(x - 1)x+1 = (-1)1 = -1.
故 x 的值为 -1 或 2.
方法总结:乘方的结果为 1,可分为三种情况:不为零的数的零次幂等于 1;1 的任何次幂都等于 1;-1 的偶次幂等于 1. 即在底数不等于 0 的情况下要考虑指数等于 0,另外还需考虑底数等于 1 或-1 的情况.
问题:计算:a3÷a5 (a ≠ 0).
解法1
解法2 假如把正整数指数幂的除法法则 am÷an = am-n
(a ≠ 0,m,n 是正整数,m>n) 中的 m>n 这个条件去掉,那么 a3÷a5 = a3-5 = a-2.
于是得到:
负整数指数幂
特别地,
总结归纳
如果令公式 am÷an = am-n 中的 m = 0,那么就会有
例3 计算:
解:
典例精析
例4 若 a = ,b = (-1)-1,c = ,则 a,b,c 的大小关系是( )
A.a>b=c B.a>c>b
C.c>a>b D.b>c>a
B
解析:a = = = ,b = (-1)-1 = -1,c =
= 1,故 a>c>b.
方法总结:关键是理解负整数指数幂的意义,依次计算出结果.当底数是分数时,只要把分子、分母颠倒,负指数就可变为正指数.
例5 把下列各数写成分数的形式:
解:
例6 计算:
解析:分别根据有理数的乘方、零指数幂、负整数指数幂及绝对值的性质计算出各数,再根据实数的运算法则进行计算.
科学记数法:绝对值大于 10 的数记成 a×10n 的形式,其中 1≤|a|<10,n 是正整数.
忆一忆:
例如,864000 可以写成 .
怎样用科学记数法表示 0.0000864?
8.64×105
想一想:
用科学计数法表示绝对值小于 1 的数
探一探:
因为
所以,0.0000864 = 8.64×0.00001 = 8.64 ×10-5.
类似地,我们可以利用 10 的负整数次幂,用科学记数法表示一些绝对值较小的数,即将它们表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.
算一算:
10-2 = ___________; 10-4 = ___________;
10-8 = ___________.
议一议:指数与运算结果的 0 的个数有什么关系?
一般地,10 的 -n 次幂,在 1 前面有_____个 0.
想一想:10-21 的小数点后的位数是几位?
1 前面有几个零?
0.01
0.0001
0.00000001
通过上面的探索,你发现了什么?
n
用科学记数法表示一些绝对值小于 1 的数的方法:
利用 10 的负整数次幂,把一个绝对值小于 1 的数表示成 a×10-n 的形式,其中 n 是正整数,1≤|a|<10.
n 等于原数第一个非零数字前所有零的个数(特别注意:包括小数点前面那个零).
知识要点
例7 用小数表示下列各数:
(1) 2×10-7; (2) 3.14×10-5;
(3) 7.08×10-3; (4) 2.17×10-1.
解析:小数点向左移动相应的位数即可.
解:(1) 2×10-7=0.0000002.
(2) 3.14×10-5=0.0000314.
(3) 7.08×10-3=0.00708.
(4) 2.17×10-1=0.217.
1. 用科学记数法表示:
(1)0.000 03; (2)-0.000 006 4;
(3)0.000 0314.
2. 用科学记数法填空:
(1)1 s 是 1 μs 的 1 000 000 倍,则 1 μs=_______s;
(2)1 mg=_______kg; (3)1 μm=_______m;
(4)1 nm=_______μm; (5)1 cm2=_______ m2;
(6)1 mL=_______m3.
练一练
3×10-5
3.14×10-5
-6.4×10-6
1×10-6
1×10-6
1×10-6
1×10-3
1×10-4
1×10-6
3. 中国女药学家屠呦呦获 2015 年诺贝尔医学奖,她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素,这是中国医学界迄今为止获得的最高奖项.已知显微镜下某种疟原虫平均长度为 0.0000015 米,该长度用科学记数法表示为__________米.
1.5×10-6
1. 计算:
1
1
64
2. 把下列各数写成分数的形式:
3. 用小数表示 5.6×10-4.
解:原式 = 5.6×0.0001 = 0.00056.
4. 比较大小:
(1)3.01×10-4_______9.5×10-3;
(2)3.01×10-4_______3.10×10-4.
<
<
5. 用科学记数法把小数 0.000 009 405 表示成
9.405×10n 的形式,那么 n = .
-6
6.计算:-32+(- )-2+(2023+π)0-|2- π|.
=-9+9+1-2+ π
= π-1.
解:-32+(- )-2+(2023+π)0-|2- π|
7. 随着微电子制造技术的不断进步,半导体材料的精加工尺寸大幅度缩小,目前已经能够在 350 平方毫米的芯片上集成 5 亿个元件,问 1 个这样的元件大约占多少平方毫米?
解析:因为 350 平方毫米的芯片上集成 5 亿个元件,说明 5 亿个元件所占的面积为 350 平方毫米,要计算 1 个元件所占的面积,可用 350 除以 5 亿.
注意:用科学记数法表示实际生活中的数量时,不能漏掉单位.
整数指数幂
非正整数
指数幂的意义
1. 零指数幂:当 a ≠ 0 时,a0 = 1
2. 负整数指数幂:当 n 是正整数时,a-n=
科学记数法表示绝对值较小的数
0.00…01
n 个 0
谢谢观看
沪科版数学七年级下册
