9.2.2 分式的加减 课件 2023-2024学年沪科版数学七年级下册(71张PPT)
文档属性
| 名称 | 9.2.2 分式的加减 课件 2023-2024学年沪科版数学七年级下册(71张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 00:00:00 | ||
图片预览









文档简介
(共71张PPT)
2.分式的加减
第9章 分 式
第1课时 分式的通分
9.2 分式的运算
沪科版数学七年级下册
1. 分式的基本性质:
分式的分子与分母都乘以(或除以)同一个________________,分式的值_______.
不变
不等于零的整式
2. 什么叫约分?
把一个分式的分子和分母的公因式约去叫做分式的约分.
回顾与思考
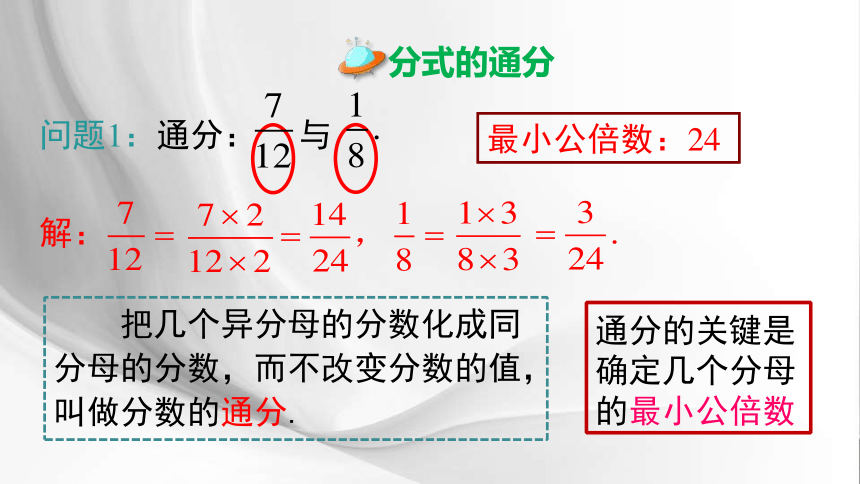
最小公倍数:24
把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分.
通分的关键是确定几个分母的最小公倍数
问题1:通分: 与
解:
分式的通分
想一想:
联想分数的通分,由上述两个问题你能想出如何将分式进行通分吗?
( b≠0 ).
问题2:填空:
知识要点
分式的通分的定义
化异分母分式为同分母分式的过程,叫做分式的通分.
如分式 与 分母分别是 ab,a2,通分后分母都变成了 a2b.
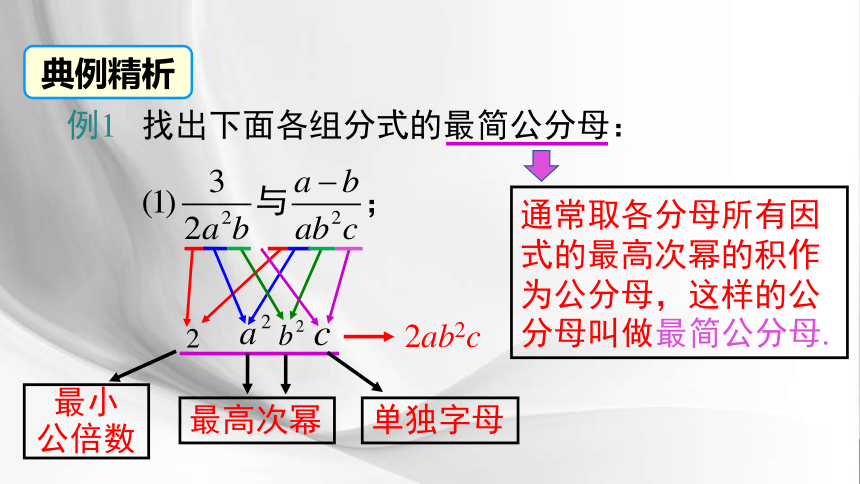
例1 找出下面各组分式的最简公分母:
最小
公倍数
最高次幂
单独字母
典例精析
通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫做最简公分母.
2ab2c
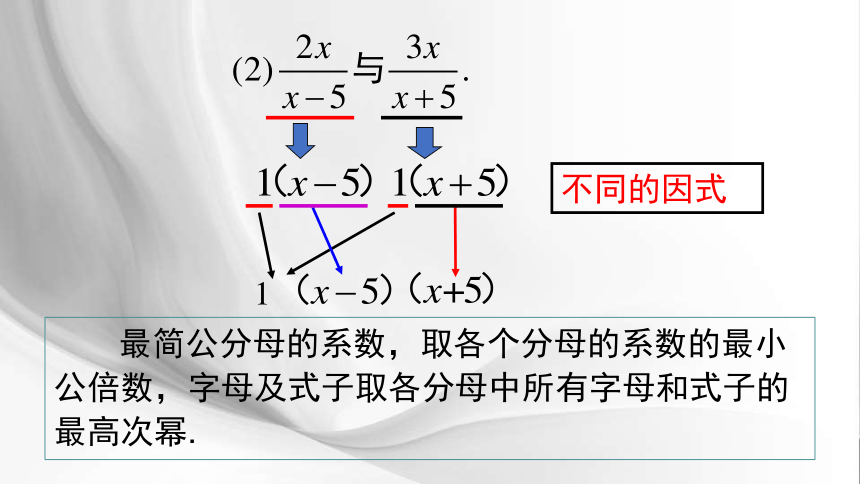
不同的因式
最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有字母和式子的最高次幂.
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
练一练
例3 通分:
解:
最简公分母是
解:
最简公分母是
确定几个分式的最简公分母的方法:
(1)因式分解;
(2)系数:取各取分式分母系数的最小公倍数;
(3)字母:取各分母的所有字母的最高次幂;
(4)多项式:取各分母所有多项式因式的最高次幂;
(5)求积.
方法归纳
解:最简公分母是
例4 通分:
解:最简公分母是
【方法总结】
① 确定最简公分母是通分的关键. 通分时,如果分母的系数是整数时,通常取它们系数的最小公倍数作为最简公分母的系数;当分母是多项式时,一般应先分解因式;
② 在确定最简公分母后,还要确定分子、分母应乘以的因式,这个因式就是最简公分母除以原分母的商.
想一想:
分数和分式在约分和通分的做法上有什么特点?这些做法的根据是什么?将答案填入下表中:
约分 通分
分数
分式
依据 找分子与分母的
最大公约数
找分子与分母的公因式
找所有分母的
最小公倍数
找所有分母的
最简公分母
分数或分式的基本性质
的最简公分母是( )
2. 分式
的最简公分母是______________.
C
1. 三个分式
B.
C.
D.
A.
4xy
3y2
12xy2
12x2y2
2x(x - 1)(x + 1)
3. 三个分式 的最简公分母是
.
x(x - 1)(x + 1)
4. 通分:
解:(1)最简公分母是 4b2d,
(2)最简公分母是 (x + y)2 (x - y),
解:(3)最简公分母是 3(a - 3)(a + 3),
(4)最简公分母是 2x(2 - x)(x + 1)(x - 1),
2. 确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1. 化异分母分式为同分母分式的过程,叫做分式的通分.
2. 确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1. 化异分母分式为同分母分式的过程,叫做分式的通分.
2.分式的加减
第9章 分 式
第2课时 分式的加减
9.2 分式的运算
沪科版数学七年级下册
1. 同分母分数的加减法则是什么?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
回顾与思考
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
a
1
a
2
+
想一想:同分母的分式应该如何加减?
类比探究
观察下列分数加减运算的式子,你想到了什么?
请类比同分母分数的加减法,说一说同分母的分式应该如何加减.
同分母分式的加减
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,分子相加减.
上述法则可用式子表示为
牛刀小试
解:原式 =
=
=
注意:结果要化为最简分式!
=
例1 计算:
典例精析
解:原式 =
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
去括号
合并同类项
注意:结果要化为最简形式!
做一做
注意:当分子是
多项式时要加括号!
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
异分母分式的加减
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
知识要点
异分母分式的加减法则
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法则进行计算.
上述法则可用式子表示为
解:原式 =
=
=
注意:(1 - x) = -(x - 1)
例2 计算:
分母不同,先化为同分母.
解:原式 =
先找出最简公分母,再正确通分,转化为同分母分式的加减
解:原式 =
=
=
注:分母是多项式的先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
例3 计算:
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
阅读下面的计算过程:
①
= ②
= ③
= ④
(1) 上述计算过程,从哪一步开始出错?请写出
该步的代号_____;
(2) 错误原因是___________;
(3) 本题的正确结果为: .
②
漏掉了分母
做一做
例4 计算:
解:原式
从 -3,1,3 中任选一个 m 值代入求值.
当 m = 1 时,原式
先化简,再求值: ,其中 .
解:
做一做
例5 已知下面一列等式:
(1) 请你根据这些等式的结构特征写出它的一般性等式;
(2) 验证你写出的等式是否成立;
(3) 利用等式计算:
①;
②;
③;
④.
解析:(1) 观察已知的四个等式,发现等式的左边是两个分数之积,这两个分数的分子都是 1,后一个分数的分母比前一个分数的分母大 1,并且第一个分数的分母与等式的序号相等,等式的右边是这两个分数之差,据此可写出一般性等式;
(2) 根据分式的运算法则验证即可;
(3) 根据(1)中的结论求解.
.
(2)因为
.
所以
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2. 填空:
4
3. 计算:
解:(1) 原式 =
(2) 原式 =
4. 先化简,再求值: ,其中 x = 2023.
当 x = 2023 时,原式
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
2.分式的加减
第9章 分 式
第3课时 分式的混合运算
9.2 分式的运算
沪科版数学七年级下册
复习引入
同分母加减:
异分母加减:
乘法:
除法:
加减法
乘方:
分式的运算法则
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
分式的混合运算
解:
先乘方,再乘除,最后加减
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
要点归纳
注意:计算结果要化为最简分式或整式.
例1 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把
其看作分母是“1”的式子.
或
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
做一做
解:原式
计算:
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高效率.
例2 计算:
利用乘法分配律简化运算
用两种方法计算:
解:(按运算顺序)
原式
做一做
解:(利用乘法分配律)
原式
例3 计算:
分析:把 和 看成整体,题目的实质是
平方差公式的应用.
解:原式
运用平方差公式
例4 先化简,再求值: ,请从
-4<x<4 的范围内选取一个合适的整数 x 代入求值.
分析:先计算括号里的,再把除法运算转化成乘法运算,进行约分化简,最后从 x 的取值范围内选取一数值代入即可.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分式分母不能为 0.
先化简,再求值: ,其中 .
解:原式 =
当 时,原式 = 3.
做一做
例5 化简繁分式:
解法1:原式
把繁分式写成分子除以分母的形式,利用除法法则化简
拓展提升
解法2:
利用分式的
基本性质化简
例6 若 ,求 A,B 的值.
解:因为
所以
解得
解析:先将等式两边化成同分母分式,然后对照两边的分子,可得到关于 A,B 的方程组.
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时可根据式子的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,对计算能力的要求较高.
总结归纳
1. 计算 的结果是( )
A.
B.
C.
D.
2. 化简 的结果是 .
3. 化简 的结果是 .
C
4. 计算
解:原式
5. 先化简: ,当 b = 3 时,再从 -2 < a < 2 的范围内选取一个合适的整数 a 代入求值.
解:原式 =
在 -2 < a < 2 中,a 可取的整数为 -1,1,
而当 b = 3,a 取 -1 时,原式的值是 ;
当 a 取 1 时,原式的值是 .
分式混合运算
混合运算
应用
关键是明确运算种类及运算顺序
明确运
算顺序
1. 同级运算自左向右进行;
2. 运算律可简化运算
运算方法及技巧
技巧
注意
谢谢观看
沪科版数学七年级下册
2.分式的加减
第9章 分 式
第1课时 分式的通分
9.2 分式的运算
沪科版数学七年级下册
1. 分式的基本性质:
分式的分子与分母都乘以(或除以)同一个________________,分式的值_______.
不变
不等于零的整式
2. 什么叫约分?
把一个分式的分子和分母的公因式约去叫做分式的约分.
回顾与思考
最小公倍数:24
把几个异分母的分数化成同分母的分数,而不改变分数的值,叫做分数的通分.
通分的关键是确定几个分母的最小公倍数
问题1:通分: 与
解:
分式的通分
想一想:
联想分数的通分,由上述两个问题你能想出如何将分式进行通分吗?
( b≠0 ).
问题2:填空:
知识要点
分式的通分的定义
化异分母分式为同分母分式的过程,叫做分式的通分.
如分式 与 分母分别是 ab,a2,通分后分母都变成了 a2b.
例1 找出下面各组分式的最简公分母:
最小
公倍数
最高次幂
单独字母
典例精析
通常取各分母所有因式的最高次幂的积作为公分母,这样的公分母叫做最简公分母.
2ab2c
不同的因式
最简公分母的系数,取各个分母的系数的最小公倍数,字母及式子取各分母中所有字母和式子的最高次幂.
找最简公分母:
x(x-5)(x+5)
(x+y)2 (x-y)
练一练
例3 通分:
解:
最简公分母是
解:
最简公分母是
确定几个分式的最简公分母的方法:
(1)因式分解;
(2)系数:取各取分式分母系数的最小公倍数;
(3)字母:取各分母的所有字母的最高次幂;
(4)多项式:取各分母所有多项式因式的最高次幂;
(5)求积.
方法归纳
解:最简公分母是
例4 通分:
解:最简公分母是
【方法总结】
① 确定最简公分母是通分的关键. 通分时,如果分母的系数是整数时,通常取它们系数的最小公倍数作为最简公分母的系数;当分母是多项式时,一般应先分解因式;
② 在确定最简公分母后,还要确定分子、分母应乘以的因式,这个因式就是最简公分母除以原分母的商.
想一想:
分数和分式在约分和通分的做法上有什么特点?这些做法的根据是什么?将答案填入下表中:
约分 通分
分数
分式
依据 找分子与分母的
最大公约数
找分子与分母的公因式
找所有分母的
最小公倍数
找所有分母的
最简公分母
分数或分式的基本性质
的最简公分母是( )
2. 分式
的最简公分母是______________.
C
1. 三个分式
B.
C.
D.
A.
4xy
3y2
12xy2
12x2y2
2x(x - 1)(x + 1)
3. 三个分式 的最简公分母是
.
x(x - 1)(x + 1)
4. 通分:
解:(1)最简公分母是 4b2d,
(2)最简公分母是 (x + y)2 (x - y),
解:(3)最简公分母是 3(a - 3)(a + 3),
(4)最简公分母是 2x(2 - x)(x + 1)(x - 1),
2. 确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1. 化异分母分式为同分母分式的过程,叫做分式的通分.
2. 确定最简分式的最简公分母的一般思路:
(1)找系数;
(2)找字母;
(3)找指数;
(4)当分母是多项式时,应先将各分母分解因式,再确定最简公分母;
(5)若分母的系数是负数,应利用符号法则,把负号提取到分式前面.
1. 化异分母分式为同分母分式的过程,叫做分式的通分.
2.分式的加减
第9章 分 式
第2课时 分式的加减
9.2 分式的运算
沪科版数学七年级下册
1. 同分母分数的加减法则是什么?
1
2. 计算:
2
同分母分数相加减,分母不变,把分子相加减.
回顾与思考
思考:类比前面同分母分数的加减,想想下面的式子该怎么计算?
a
1
a
2
+
想一想:同分母的分式应该如何加减?
类比探究
观察下列分数加减运算的式子,你想到了什么?
请类比同分母分数的加减法,说一说同分母的分式应该如何加减.
同分母分式的加减
知识要点
同分母分式的加减法则
同分母分式相加减,分母不变,分子相加减.
上述法则可用式子表示为
牛刀小试
解:原式 =
=
=
注意:结果要化为最简分式!
=
例1 计算:
典例精析
解:原式 =
=
=
注意:结果要化为最简分式!
=
把分子看作一个整体,先用括号括起来!
去括号
合并同类项
注意:结果要化为最简形式!
做一做
注意:当分子是
多项式时要加括号!
问题:
请计算 ( ), ( ).
异分母分数相加减
分数的通分
依据:分数的基本性质
转化
同分母分数的加减
异分母分数相加减,先通分,
变为同分母的分数,再加减.
异分母分式的加减
请计算 ( ), ( ).
依据:分数基本性质
分数的通分
同分母分数相加减
异分母分数相加减
转化
异分母分数相加减,先通分,变为同分母的分数,再加减.
异分母分式相加减
分式的通分
依据:分式基本性质
转化
同分母分式相加减
异分母分式相加减,先通分,变为同分母的分式,再加减.
请思考
b
d
b
d
类比:异分母的分式应该如何加减
知识要点
异分母分式的加减法则
异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法则进行计算.
上述法则可用式子表示为
解:原式 =
=
=
注意:(1 - x) = -(x - 1)
例2 计算:
分母不同,先化为同分母.
解:原式 =
先找出最简公分母,再正确通分,转化为同分母分式的加减
解:原式 =
=
=
注:分母是多项式的先分解因式
先找出最简公分母,再正确通分,转化为同分母的分式相加减.
=
知识要点
分式的加减法的思路
通分
转化为
异分母相加减
同分母
相加减
分子(整式)相加减
分母不变
转化为
例3 计算:
法一:
原式 =
法二:
原式 =
把整式看成分母为“1”的式子
阅读下面的计算过程:
①
= ②
= ③
= ④
(1) 上述计算过程,从哪一步开始出错?请写出
该步的代号_____;
(2) 错误原因是___________;
(3) 本题的正确结果为: .
②
漏掉了分母
做一做
例4 计算:
解:原式
从 -3,1,3 中任选一个 m 值代入求值.
当 m = 1 时,原式
先化简,再求值: ,其中 .
解:
做一做
例5 已知下面一列等式:
(1) 请你根据这些等式的结构特征写出它的一般性等式;
(2) 验证你写出的等式是否成立;
(3) 利用等式计算:
①;
②;
③;
④.
解析:(1) 观察已知的四个等式,发现等式的左边是两个分数之积,这两个分数的分子都是 1,后一个分数的分母比前一个分数的分母大 1,并且第一个分数的分母与等式的序号相等,等式的右边是这两个分数之差,据此可写出一般性等式;
(2) 根据分式的运算法则验证即可;
(3) 根据(1)中的结论求解.
.
(2)因为
.
所以
A. B. C.-1 D.2
1. 计算
的结果为( )
C
2. 填空:
4
3. 计算:
解:(1) 原式 =
(2) 原式 =
4. 先化简,再求值: ,其中 x = 2023.
当 x = 2023 时,原式
分式加减运算
加减运算法则
注意点
异分母分式相加减先转化为同分母分式的加减运算
(2) 整式和分式之间进行加减运算时,则要把整式看成分母是 1 的式子,以便通分
(3) 异分母分式进行加减运算需要先通分,关键是确定最简公分母
(1) 若分式作为减式,则运算时要注意适时添加括号
2.分式的加减
第9章 分 式
第3课时 分式的混合运算
9.2 分式的运算
沪科版数学七年级下册
复习引入
同分母加减:
异分母加减:
乘法:
除法:
加减法
乘方:
分式的运算法则
问题:如何计算 ?
请先思考这道题包含的运算,确定运算顺序,再独立完成.
分式的混合运算
解:
先乘方,再乘除,最后加减
分式的混合运算顺序
先算乘方,再算乘除,最后算加减,有括号的先算括号里面的.
要点归纳
注意:计算结果要化为最简分式或整式.
例1 计算:
解:原式
先算括号里的加法,再算括号外的乘法
注:当式子中出现整式时,把整式看成整体,并把
其看作分母是“1”的式子.
或
解:原式
注意:分子或分母是多项式的先因式分解,不能分解的要视为整体.
做一做
解:原式
计算:
解:原式
方法总结:观察题目的结构特点,灵活运用运算律,适当运用计算技巧,可简化运算,提高效率.
例2 计算:
利用乘法分配律简化运算
用两种方法计算:
解:(按运算顺序)
原式
做一做
解:(利用乘法分配律)
原式
例3 计算:
分析:把 和 看成整体,题目的实质是
平方差公式的应用.
解:原式
运用平方差公式
例4 先化简,再求值: ,请从
-4<x<4 的范围内选取一个合适的整数 x 代入求值.
分析:先计算括号里的,再把除法运算转化成乘法运算,进行约分化简,最后从 x 的取值范围内选取一数值代入即可.
方法总结:把分式化成最简分式是解题的关键,通分、因式分解和约分是基本环节,注意选数时,要求分式分母不能为 0.
先化简,再求值: ,其中 .
解:原式 =
当 时,原式 = 3.
做一做
例5 化简繁分式:
解法1:原式
把繁分式写成分子除以分母的形式,利用除法法则化简
拓展提升
解法2:
利用分式的
基本性质化简
例6 若 ,求 A,B 的值.
解:因为
所以
解得
解析:先将等式两边化成同分母分式,然后对照两边的分子,可得到关于 A,B 的方程组.
分式的混合运算
(1)进行混合运算时,要注意运算顺序,在没有括号的情况下,按从左往右的方向,先算乘方,再算乘除,后算加减;
(2)分式的混合运算,一般按常规运算顺序,但有时可根据式子的特点,运用乘法的运算律进行灵活运算.
混合运算的特点:是整式运算、因式分解、分式运算的综合运用,对计算能力的要求较高.
总结归纳
1. 计算 的结果是( )
A.
B.
C.
D.
2. 化简 的结果是 .
3. 化简 的结果是 .
C
4. 计算
解:原式
5. 先化简: ,当 b = 3 时,再从 -2 < a < 2 的范围内选取一个合适的整数 a 代入求值.
解:原式 =
在 -2 < a < 2 中,a 可取的整数为 -1,1,
而当 b = 3,a 取 -1 时,原式的值是 ;
当 a 取 1 时,原式的值是 .
分式混合运算
混合运算
应用
关键是明确运算种类及运算顺序
明确运
算顺序
1. 同级运算自左向右进行;
2. 运算律可简化运算
运算方法及技巧
技巧
注意
谢谢观看
沪科版数学七年级下册
