3.1.2等式的性质 课件 人教版七年级数学上册(20张PPT)
文档属性
| 名称 | 3.1.2等式的性质 课件 人教版七年级数学上册(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 10:58:42 | ||
图片预览







文档简介
3.1.2 等式的性质
七年级上
人教版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握等式的基本性质;
2. 能运用等式的基本性质解简单的一元一次方程.
学习目标
重点
难点
利用方程求出未知数的解.
(1) 3x = 24
解:因为 3×8 = 24,
所以 x = 8.
(2) x +1 = 3
解:因为 2+1 = 3,
所以 x = 2.
新课引入
你会解方程
5x+4=0吗?
我们可以直接看出像3x = 24,x+1=3这样的简单方程的解,但是仅靠观察来解比较复杂的方程是困难的.因此,我们还要讨论怎样解方程.方程是含有未知数的等式,为了讨论解方程,我们先来看看等式有什么性质.
像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y这样的式子,都是等式.我们可以用a=b表示一般的等式.
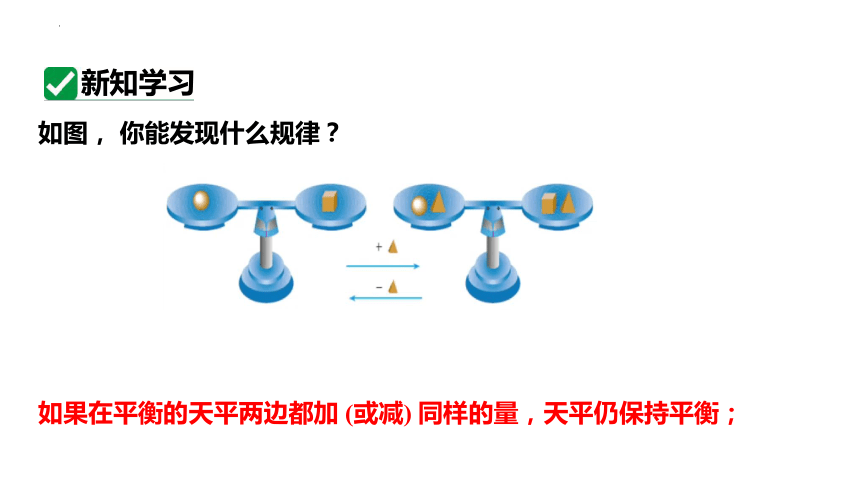
如图, 你能发现什么规律?
如果在平衡的天平两边都加 (或减) 同样的量,天平仍保持平衡;
新知学习
归纳
等式的性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果 a = b,那么 a ± c = b ± c.
等式就像平衡的天平,它具有与上面的事实同样的性质.
例1 根据等式性质填空
(1) 如果 a = 2,那么 a + 3 = 2 __________.
依据是等式的性质 _____,
在等式的两边都 ________________________;
+ 3
1
加同一个数,结果仍相等
(2) 如果 a = 2,那么 a – 5 = 2 __________.
依据是等式的性质 _____,
在等式的两边都 _______________________.
- 5
1
减同一个数,结果仍相等
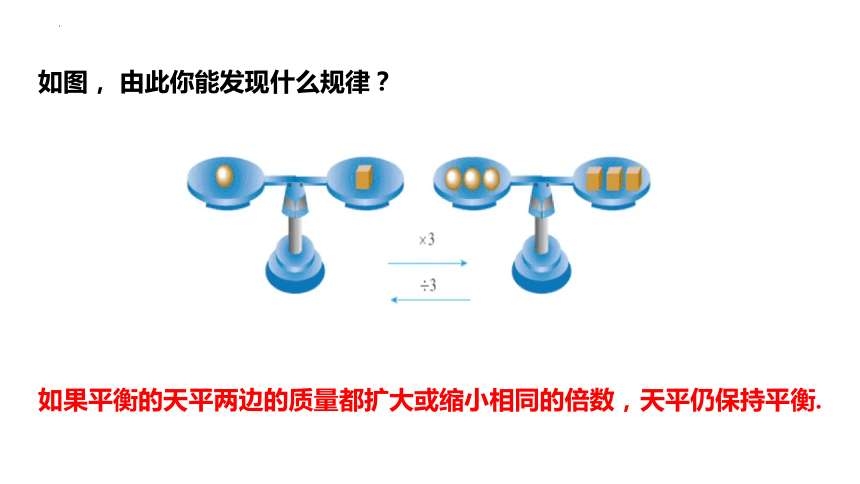
如图, 由此你能发现什么规律?
如果平衡的天平两边的质量都扩大或缩小相同的倍数,天平仍保持平衡.
等式的性质2: 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 a = b,那么 ac = bc;
如果 a = b (c ≠ 0),那么 ???????? = ???????? .
?
归纳
同理,我们可以得到:
例2 根据等式性质填空
(1) 如果 a = 2,那么 – 3a = 2 __________.
依据是等式的性质 _____,
在等式的两边都 ________________________.
×(-3)
2
(2) 如果 a = 2,那么 = __________.
依据是等式的性质 _____,
在等式的两边都 _______________________________.
乘同一个数,结果仍相等
2
除以同一个不为 0 数,结果仍相等
例3 利用等式的性质解下列方程:
(1) x+7=26 ;
解:(1) 两边减 7,得 x+7-7=26-7 ,
于是 x = 19.
分析:要使方程x+7=26转化为x=a(常数)的形式,需去掉方程左边的7,利用等式的性质1,方程两边减7就得出x的值.
(2) -5x=20 ;
分析:要使方程-5x=20 转化为x=a(常数)的形式,需去掉方程左边的-5,利用等式的性质2,方程两边除以5就得出x的值.
(2) 两边除以 -5,得 ,
于是 x = -4.
?????????????? = ?????????????
?
(3)
解:(3) 两边加 5,得 ,
化简,得 .
两边乘-3,得 x = -27.
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据.
-????????x -5= 4
?
-????????x -5+5= 4+5
?
-????????x =9
?
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.例如,
将x=27代入方程 的左边,得
方程的左右两边相等,所以x=-27是方程 的解.
-????????× (-27)-5
= 9-5=4
?
-????????x -5= 4
?
-????????x -5= 4
?
1.已知 3a + b - 2 = 7a + b - 2,以下是某同学的变形过程,请找出变形过程中的错误.
解:两边加 2,得 3a + b = 7a + b.
两边减 b,得 3a = 7a.
两边除以 a,得 3 = 7.
分析:3a = 7a,可知 a = 0,0 不能做除数.
随堂练习
2.利用等式的性质解下列方程并检验.
(1) 0.3x=45 ;
解:(1) 两边除以0.3,得 ,
于是 x = 150.
????.????????????.???? = ????????????.????
?
将x = 150代入方程0.3x=45的左边,得
0.3×150=45,
方程的左右两边相等,所以x=150是方程0.3x=45 的解.
(2) 5x+4=0;
解:(1) 两边减4,得 5x+4-4=0-4,
化简,得 5x=-4
两边除以5,得 ,
得 x = .
???????????? = ?????????
?
?????????
?
将x = 代入方程5x+4=0的左边,得
5× +4 =0,
方程的左右两边相等,所以x= 是方程5x+4=0的解.
?????????
?
?????????
?
?????????
?
(2) ;
?????????????x =3
?
解:(1) 两边减2,得 ,
化简,得 =1
两边×(-4),得 ,
得 x =-4 .
??????? x×(-4)= ????×(?????)
?
?????????????x-2 =3-2
?
?????????x
?
将x = -4代入方程 的左边,得
方程的左右两边相等,所以x= -4是方程 的解.
?????????????x =3
?
?????????????×(-4) =3
?
?????????????x =3
?
性质2
性质1
等式的性质
等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等.
如果 a = b,那么ac = bc .
如果 a = b (c ≠ 0),那么
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果 a = b,那么 a ± c = b ± c.
课堂小结
七年级上
人教版
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1. 掌握等式的基本性质;
2. 能运用等式的基本性质解简单的一元一次方程.
学习目标
重点
难点
利用方程求出未知数的解.
(1) 3x = 24
解:因为 3×8 = 24,
所以 x = 8.
(2) x +1 = 3
解:因为 2+1 = 3,
所以 x = 2.
新课引入
你会解方程
5x+4=0吗?
我们可以直接看出像3x = 24,x+1=3这样的简单方程的解,但是仅靠观察来解比较复杂的方程是困难的.因此,我们还要讨论怎样解方程.方程是含有未知数的等式,为了讨论解方程,我们先来看看等式有什么性质.
像m+n=n+m,x+2x=3x,3×3+1=5×2,3x+1=5y这样的式子,都是等式.我们可以用a=b表示一般的等式.
如图, 你能发现什么规律?
如果在平衡的天平两边都加 (或减) 同样的量,天平仍保持平衡;
新知学习
归纳
等式的性质1:等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果 a = b,那么 a ± c = b ± c.
等式就像平衡的天平,它具有与上面的事实同样的性质.
例1 根据等式性质填空
(1) 如果 a = 2,那么 a + 3 = 2 __________.
依据是等式的性质 _____,
在等式的两边都 ________________________;
+ 3
1
加同一个数,结果仍相等
(2) 如果 a = 2,那么 a – 5 = 2 __________.
依据是等式的性质 _____,
在等式的两边都 _______________________.
- 5
1
减同一个数,结果仍相等
如图, 由此你能发现什么规律?
如果平衡的天平两边的质量都扩大或缩小相同的倍数,天平仍保持平衡.
等式的性质2: 等式两边乘同一个数,或除以同一个不为0的数,结果仍相等.
如果 a = b,那么 ac = bc;
如果 a = b (c ≠ 0),那么 ???????? = ???????? .
?
归纳
同理,我们可以得到:
例2 根据等式性质填空
(1) 如果 a = 2,那么 – 3a = 2 __________.
依据是等式的性质 _____,
在等式的两边都 ________________________.
×(-3)
2
(2) 如果 a = 2,那么 = __________.
依据是等式的性质 _____,
在等式的两边都 _______________________________.
乘同一个数,结果仍相等
2
除以同一个不为 0 数,结果仍相等
例3 利用等式的性质解下列方程:
(1) x+7=26 ;
解:(1) 两边减 7,得 x+7-7=26-7 ,
于是 x = 19.
分析:要使方程x+7=26转化为x=a(常数)的形式,需去掉方程左边的7,利用等式的性质1,方程两边减7就得出x的值.
(2) -5x=20 ;
分析:要使方程-5x=20 转化为x=a(常数)的形式,需去掉方程左边的-5,利用等式的性质2,方程两边除以5就得出x的值.
(2) 两边除以 -5,得 ,
于是 x = -4.
?????????????? = ?????????????
?
(3)
解:(3) 两边加 5,得 ,
化简,得 .
两边乘-3,得 x = -27.
解以x为未知数的方程,就是把方程逐步转化为x=a(常数)的形式,等式的性质是转化的重要依据.
-????????x -5= 4
?
-????????x -5+5= 4+5
?
-????????x =9
?
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.例如,
将x=27代入方程 的左边,得
方程的左右两边相等,所以x=-27是方程 的解.
-????????× (-27)-5
= 9-5=4
?
-????????x -5= 4
?
-????????x -5= 4
?
1.已知 3a + b - 2 = 7a + b - 2,以下是某同学的变形过程,请找出变形过程中的错误.
解:两边加 2,得 3a + b = 7a + b.
两边减 b,得 3a = 7a.
两边除以 a,得 3 = 7.
分析:3a = 7a,可知 a = 0,0 不能做除数.
随堂练习
2.利用等式的性质解下列方程并检验.
(1) 0.3x=45 ;
解:(1) 两边除以0.3,得 ,
于是 x = 150.
????.????????????.???? = ????????????.????
?
将x = 150代入方程0.3x=45的左边,得
0.3×150=45,
方程的左右两边相等,所以x=150是方程0.3x=45 的解.
(2) 5x+4=0;
解:(1) 两边减4,得 5x+4-4=0-4,
化简,得 5x=-4
两边除以5,得 ,
得 x = .
???????????? = ?????????
?
?????????
?
将x = 代入方程5x+4=0的左边,得
5× +4 =0,
方程的左右两边相等,所以x= 是方程5x+4=0的解.
?????????
?
?????????
?
?????????
?
(2) ;
?????????????x =3
?
解:(1) 两边减2,得 ,
化简,得 =1
两边×(-4),得 ,
得 x =-4 .
??????? x×(-4)= ????×(?????)
?
?????????????x-2 =3-2
?
?????????x
?
将x = -4代入方程 的左边,得
方程的左右两边相等,所以x= -4是方程 的解.
?????????????x =3
?
?????????????×(-4) =3
?
?????????????x =3
?
性质2
性质1
等式的性质
等式两边乘同一个数,或除以同一个不为 0 的数,结果仍相等.
如果 a = b,那么ac = bc .
如果 a = b (c ≠ 0),那么
等式两边加 (或减) 同一个数 (或式子),结果仍相等.
如果 a = b,那么 a ± c = b ± c.
课堂小结
