1.3线段的垂直平分线 自主学习解答题专题提升训练题 (含答案)2023-2024学年北师大版八年级数学下册
文档属性
| 名称 | 1.3线段的垂直平分线 自主学习解答题专题提升训练题 (含答案)2023-2024学年北师大版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 817.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 11:30:41 | ||
图片预览



文档简介
2023-2024学年北师大版八年级数学下册《1.3线段的垂直平分线》
自主学习解答题专题提升训练题(附答案)
1.尺规作图:画出线段AB的垂直平分线(不写作法,保留作图痕迹)
2.如图,已知△ABC,请用直尺与圆规作图,将三角形的面积两等分.(不写作法,但要保留作图痕迹)
3.如图,在△ABC中,DE是AC的垂直平分线,AE=6,△ABD的周长为24.
求△ABC的周长
4.如图在△ABC中,AB=AC,直线DE垂直平分AB,若∠A=40°,则
(1)求∠DBC的度数,
(2)若AB=12,BC=7,求△BCD的周长
5.如图,等腰三角形的底边长为4,的面积是16,腰的垂直平分线分别交边于点.若为边的中点,为线段上一动点,求周长的最小值.
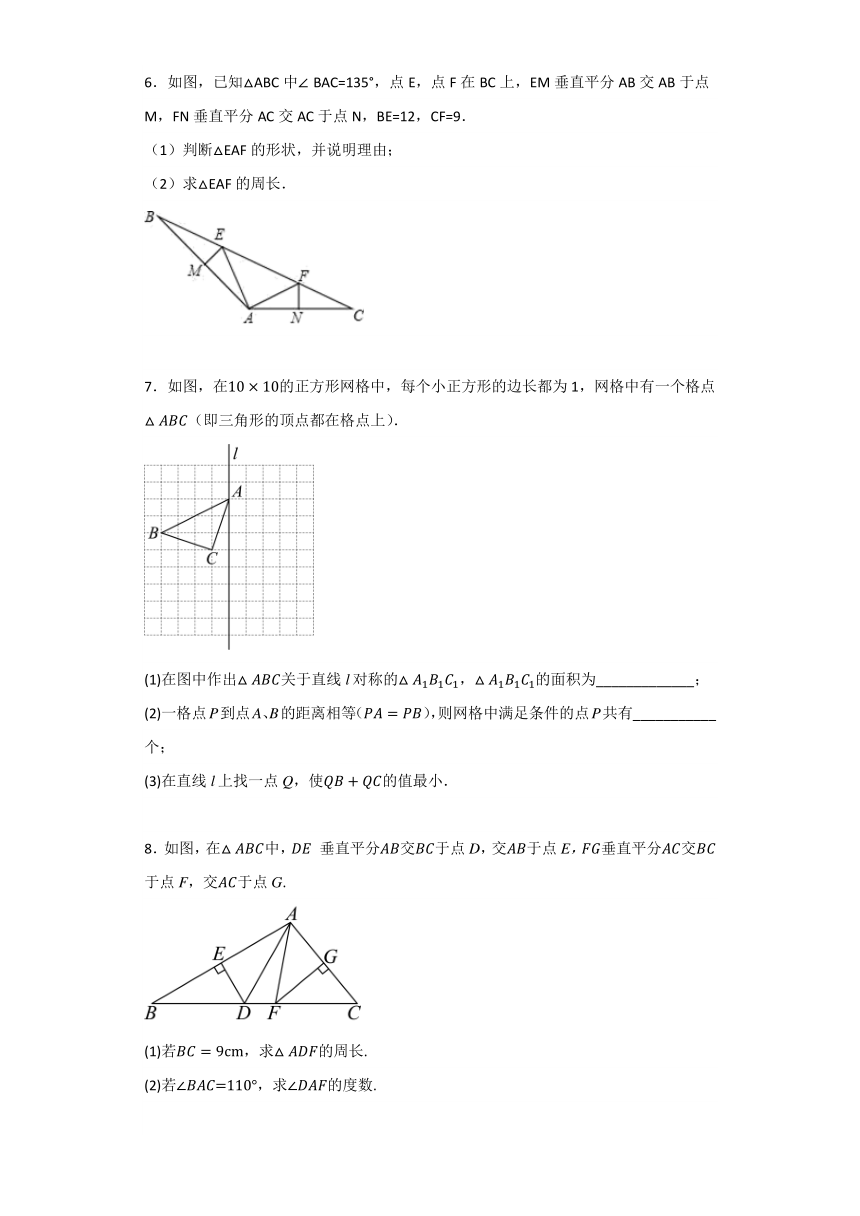
6.如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
7.如图,在的正方形网格中,每个小正方形的边长都为1,网格中有一个格点(即三角形的顶点都在格点上).
(1)在图中作出关于直线l对称的,的面积为_____________;
(2)一格点P到点A、B的距离相等(),则网格中满足条件的点P共有___________个;
(3)在直线l上找一点Q,使的值最小.
8.如图,在中, 垂直平分交于点D,交于点E,垂直平分交于点F,交于点G.
(1)若,求的周长.
(2)若,求的度数.
9.如图,在四边形中,,点E为上一点,连接相交于点F,.
(1)判断的形状,并说明理由.
(2)若,求的长.
10.如图,在四边形中,,为的中点,连接,,延长交的延长线于点.
(1)求证:点是的中点;
(2)若,,求的长.
11.如图,在中,是边的垂直平分线,且,延长,交于点F,连接.
(1)求证:;
(2)若,,求的长.
12.如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线:过点,与轴交于点.
(1)求直线的函数表达式;
(2)如图2,线段的垂直平分线交于点,求点的坐标;
(3)若点在线段上,且,求点的坐标.
13.如图,在中,,的垂真平分线交于点,交于点.
(1)若,则的度数是 度;
(2)探究与的关系,并说明理由;
(3)连接,若,的周长是,求的长.
14.如图,已知垂直平分线段,点是线段延长线上的一点,且,连接,过点作于点,交的延长线于点.
(1)______;(用含的代数式表示)
(2)求证:;
(3)若,求的面积.
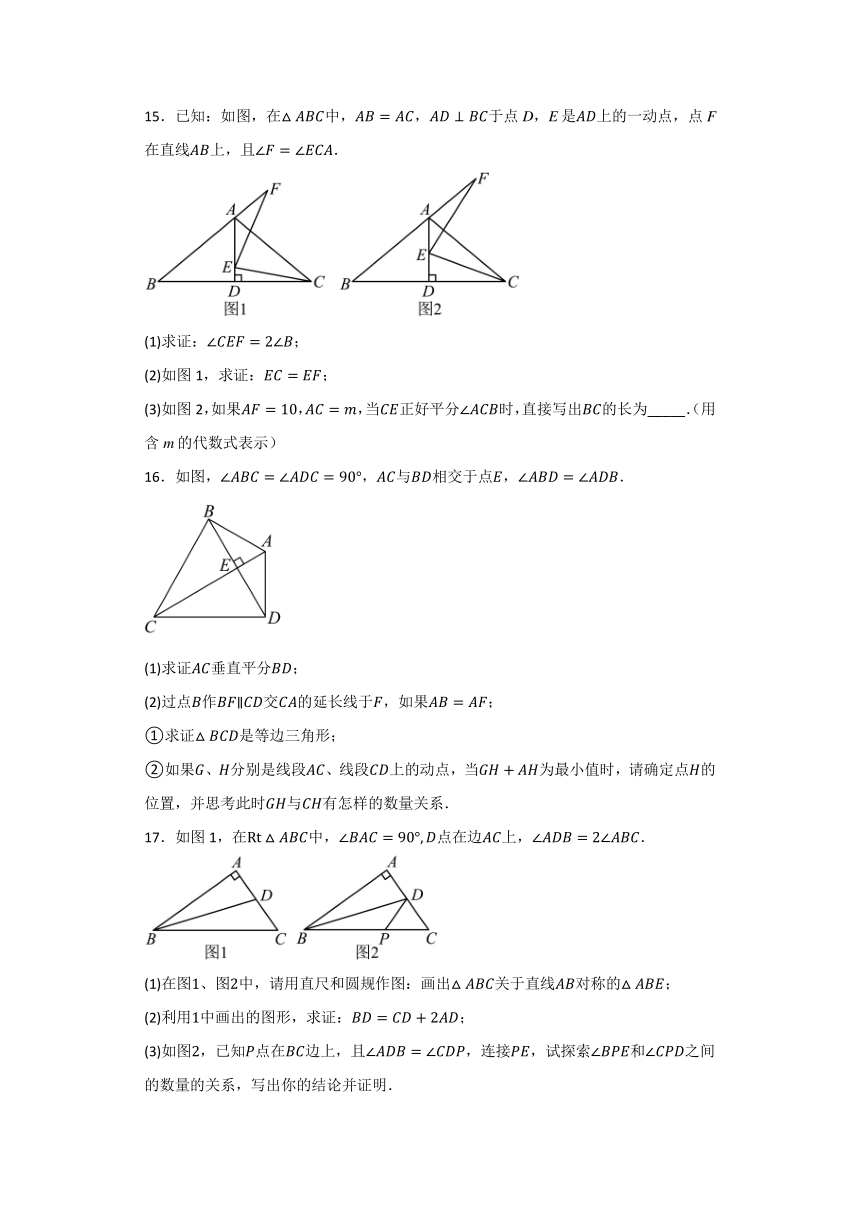
15.已知:如图,在中,,于点D,E是上的一动点,点F在直线上,且.
(1)求证:;
(2)如图1,求证:;
(3)如图2,如果,,当正好平分时,直接写出的长为_____.(用含m的代数式表示)
16.如图,,与相交于点,.
(1)求证垂直平分;
(2)过点作交的延长线于,如果;
①求证是等边三角形;
②如果、分别是线段、线段上的动点,当为最小值时,请确定点的位置,并思考此时与有怎样的数量关系.
17.如图1,在中,点在边上,.
(1)在图、图中,请用直尺和圆规作图:画出关于直线对称的;
(2)利用中画出的图形,求证:;
(3)如图,已知点在边上,且,连接,试探索和之间的数量的关系,写出你的结论并证明.
18.在中,,点D是上一点,,点E是上一点,.
(1)如图1,求证:是等腰三角形.
(2)如图2,过点E作于点F,求证:平分.
(3)如图3,延长交于点G,求证:点C在的垂直平分线上.
19.【教材呈现】以下是人教版八年级上册数学教材第53页的部分内容.
如图1,四边形中,,.我们把这种两组邻边分别相等的四边形叫做“筝形”.
【性质探究】
(1)如图1,连接筝形的对角线、交于点O,试探究筝形的性质,并填空:对角线、的关系是: ;图中、的大小关系是: .
【概念理解】
(2)如图2,在中,,垂足为,与关于所在的直线对称,与关于所在的直线对称,延长,相交于点.请写出图中所有的“筝形”,并选择其中一个进行证明;
【应用拓展】
(3)如图3,在(2)的条件下,连接,分别交、于点、.求证:.
20.(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围,小聪同学是这样思考的:延长至,使,连接.利用全等将边转化到,在中利用三角形三边关系即可求出中线的取值范围,在这个过程中小聪同学证三角形全等用到的判定方法是______,中线的取值范围是______;
(2)问题解决:如图2,在中,点是的中点,.交于点,交于点.求证:;
(3)问题拓展:如图3,在中,点是的中点,分别以,为直角边向外作和,其中,,,连接,请你探索与的数量与位置关系.
参考答案
1.解:如图所示:EF即为所求.
2.解:如图:
3.解:∵DE是AC的垂直平分线,
∴AD=CD,AE=CE=6,
∴AC=12.
∵△ABD的周长为24,
∴AB+BD+AC=AB+BD+CD=AB+BC=24,
∴△ABC的周长为:AB+BC+AC=36.
4.解:(1)在中,,,
∴.
又∵垂直平分,
∴,
∴,
∴.
(2)∵,∴,
∴.
答:的周长为19.
5.解:连接,.
是等腰三角形,点是边的中点,
,
,
解得,
是线段的垂直平分线,
点关于直线的对称点为点,,
,
的长为的最小值,
的周长最短.
故答案为:10.
6.解:(1)△EAF为直角三角形.
∵EM是AB的垂直平分线,
∴BE=AE,
∴∠BAE=∠B.
∵FN是AC的垂直平分线,
∴AF=CF,
∴∠CAF=∠C
.∵∠BAC=135°,
∴∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,
∴∠BAE+∠CAF=45°,
∴∠EAF=135°﹣45°=90°,
∴△EAF为直角三角形;
(2)在△EAF中,
∵∠EAF=90°,
∴EF2=AE2+AF2,
∵BE=12,CF=9,
∴EF2=122+92=225,
∴EF=15,
∴△EAF的周长=12+9+15=36.
故答案为(1)△EAF为直角三角形.理由见解析;(2)△EAF的周长=36.
7.(1)解:根据轴对称图形的性质,
如图所示,即为所求:
.
(2)根据垂直平分线的性质,
作线段的垂直平分线,如图:
点、、、、都满足条件,
则网格中满足条件的点P共有5个,
故答案为:5.
(3)连接与直线交于点Q,
由轴对称图形的性质得,
,
则此时值最小,
如图所示,点Q即为所求:
8.(1)解:垂直平分
,
垂直平分
,
的周长
(2)在中,
,
,
垂直平分,
,
垂直平分,
,
,,
9.(1)解:是等边三角形,理由如下:
∵,
∴是等边三角形.
∴.
∵,
∴,
∴,
∴是等边三角形;
(2)解:连接交于点O,
∵,
∴是的垂直平分线,
即.
∵,
∴.
∵,
∴,
∴,
∴.
∵是等边三角形,
∴,
∴.
10.(1)证明:,
,
是的中点,
,
在与中,
,
,即点是的中点;
(2)解:,
,
又,,
是线段的垂直平分线,
,
,
.
11.(1)证明:如图,连接,
∵是边的垂直平分线,
∴.
∵,
∴,即.
∴是直角三角形.
∴;
(2)解:设,则,
∵,
∴.
∵,,
∴.
∴,
解得.
∴.
12.(1)解:∵点A在轴上,直线过点A,
∴点A坐标为
将点和点代入直线,得,
解得,
∴直线的函数表达式为;
(2)解:∵的垂直平分线交于点,
∴点的横坐标为,
将,代入,得,
∴点的坐标为;
(3)解:如图,设点坐标为,
在中,令得,
∴,
∵,,
∴,,,
∵点在线段上,,
∴,
解得:,
当时,,
∴点的坐标为.
13.(1)解: ,,
,
,
垂直平分,
,
,
故答案为:50;
(2)解:,
理由如下:∵,
∴,
∴,
∵,
∴;
(3)解:如图,
∵是线段的垂直平分线,
∴,
∴,
∵,,的周长是,
∴.
14.(1)解: ,
,
,
,
,
,
故答案为:;
(2)证明:如图,连接.
垂直平分线段,
,
.
,
,
,
,
由(1)知,
,
,
;
(3)解:垂直平分线段,
,
如图,过点作,交的延长线于点,则.
,
,
.
,
,
在和中,
,
,
,
,
,
.
15.(1)证明:如图,设与交与点G,
,于点D,
,
,,
,
;
(2)如图,连接,
,,
,
垂直平分,
,
,
,
,
,
,
,
;
(3)如图,连接,
,,
,
垂直平分,
,
,
平分,
,
,,
,
,
,
,
故答案为:.
16.(1)证明:∵,
∴,
又∵,,
∴,
∴,
又∵,
∴垂直平分;
(2)①证明:如图,
∵,
∴,
∴,
∵,
∴,
由(1)知,,
∴,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
又∵,
∴是等边三角形;
②如图,延长至使得,则垂直平分线,
∴,
∴,
作于G,则此时取最小值,
∵是等边三角形,,
∴,
∴在中,.
17.解:(1)如图,延长,以点为圆心长为半径画弧,交延长线与点,连接,
∴即为所求;
(2)如图,同()作点关于对称点,连接
∴,
∵,,,
∴,
∴,
∵,,
∴是垂直平分线,
∴,
∴,
∴,
∴,
∵,,
∴;
(3),理由:
如图,
设,
∵,
∴,
在中,,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴,
在中,
,
∴,
∴.
18.解:(1),,
,
,
,
,
∴,
∴,
是等腰三角形;
(2)过点D作,
,
,
∴,
,
是等腰三角形,
,
,
,
,
平分;
(3)由(2),
在中,,
在中,,
∴
,
∴,
∴
∴点在的垂直平分线上.
19.解:(1)∵,,
∴垂直平分,
∵,,
∴;
(2)图中的“筝形”有:四边形、四边形、四边形;
证明四边形是筝形:
由轴对称的性质可知,;
四边形是筝形.
同理:,;
四边形是筝形.
连接,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形是筝形;
(3)证明:如图3中,
由轴对称的性质可知:
,,,,
∴,,
,
,
,
,
.
20.解:(1)如图1,延长至,使,连接,
∵为边上的中线,,,
∴,
在和中,
,
∴,
∴,
在中,根据三角形三边关系可得:,
即,
∵,
∴,
∴,
故答案为:,;
(2)如图2中,延长至点,使,连接,
∵点是的中点,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
在中,由三角形的三边关系得:,
∴;
(3)结论:,,
如图3,延长于,使得,连接,延长交于,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∴,
即.
自主学习解答题专题提升训练题(附答案)
1.尺规作图:画出线段AB的垂直平分线(不写作法,保留作图痕迹)
2.如图,已知△ABC,请用直尺与圆规作图,将三角形的面积两等分.(不写作法,但要保留作图痕迹)
3.如图,在△ABC中,DE是AC的垂直平分线,AE=6,△ABD的周长为24.
求△ABC的周长
4.如图在△ABC中,AB=AC,直线DE垂直平分AB,若∠A=40°,则
(1)求∠DBC的度数,
(2)若AB=12,BC=7,求△BCD的周长
5.如图,等腰三角形的底边长为4,的面积是16,腰的垂直平分线分别交边于点.若为边的中点,为线段上一动点,求周长的最小值.
6.如图,已知△ABC中∠BAC=135°,点E,点F在BC上,EM垂直平分AB交AB于点M,FN垂直平分AC交AC于点N,BE=12,CF=9.
(1)判断△EAF的形状,并说明理由;
(2)求△EAF的周长.
7.如图,在的正方形网格中,每个小正方形的边长都为1,网格中有一个格点(即三角形的顶点都在格点上).
(1)在图中作出关于直线l对称的,的面积为_____________;
(2)一格点P到点A、B的距离相等(),则网格中满足条件的点P共有___________个;
(3)在直线l上找一点Q,使的值最小.
8.如图,在中, 垂直平分交于点D,交于点E,垂直平分交于点F,交于点G.
(1)若,求的周长.
(2)若,求的度数.
9.如图,在四边形中,,点E为上一点,连接相交于点F,.
(1)判断的形状,并说明理由.
(2)若,求的长.
10.如图,在四边形中,,为的中点,连接,,延长交的延长线于点.
(1)求证:点是的中点;
(2)若,,求的长.
11.如图,在中,是边的垂直平分线,且,延长,交于点F,连接.
(1)求证:;
(2)若,,求的长.
12.如图,在平面直角坐标系中,直线:与轴交于点,与轴交于点,直线:过点,与轴交于点.
(1)求直线的函数表达式;
(2)如图2,线段的垂直平分线交于点,求点的坐标;
(3)若点在线段上,且,求点的坐标.
13.如图,在中,,的垂真平分线交于点,交于点.
(1)若,则的度数是 度;
(2)探究与的关系,并说明理由;
(3)连接,若,的周长是,求的长.
14.如图,已知垂直平分线段,点是线段延长线上的一点,且,连接,过点作于点,交的延长线于点.
(1)______;(用含的代数式表示)
(2)求证:;
(3)若,求的面积.
15.已知:如图,在中,,于点D,E是上的一动点,点F在直线上,且.
(1)求证:;
(2)如图1,求证:;
(3)如图2,如果,,当正好平分时,直接写出的长为_____.(用含m的代数式表示)
16.如图,,与相交于点,.
(1)求证垂直平分;
(2)过点作交的延长线于,如果;
①求证是等边三角形;
②如果、分别是线段、线段上的动点,当为最小值时,请确定点的位置,并思考此时与有怎样的数量关系.
17.如图1,在中,点在边上,.
(1)在图、图中,请用直尺和圆规作图:画出关于直线对称的;
(2)利用中画出的图形,求证:;
(3)如图,已知点在边上,且,连接,试探索和之间的数量的关系,写出你的结论并证明.
18.在中,,点D是上一点,,点E是上一点,.
(1)如图1,求证:是等腰三角形.
(2)如图2,过点E作于点F,求证:平分.
(3)如图3,延长交于点G,求证:点C在的垂直平分线上.
19.【教材呈现】以下是人教版八年级上册数学教材第53页的部分内容.
如图1,四边形中,,.我们把这种两组邻边分别相等的四边形叫做“筝形”.
【性质探究】
(1)如图1,连接筝形的对角线、交于点O,试探究筝形的性质,并填空:对角线、的关系是: ;图中、的大小关系是: .
【概念理解】
(2)如图2,在中,,垂足为,与关于所在的直线对称,与关于所在的直线对称,延长,相交于点.请写出图中所有的“筝形”,并选择其中一个进行证明;
【应用拓展】
(3)如图3,在(2)的条件下,连接,分别交、于点、.求证:.
20.(1)阅读理解:如图1,在中,若,.求边上的中线的取值范围,小聪同学是这样思考的:延长至,使,连接.利用全等将边转化到,在中利用三角形三边关系即可求出中线的取值范围,在这个过程中小聪同学证三角形全等用到的判定方法是______,中线的取值范围是______;
(2)问题解决:如图2,在中,点是的中点,.交于点,交于点.求证:;
(3)问题拓展:如图3,在中,点是的中点,分别以,为直角边向外作和,其中,,,连接,请你探索与的数量与位置关系.
参考答案
1.解:如图所示:EF即为所求.
2.解:如图:
3.解:∵DE是AC的垂直平分线,
∴AD=CD,AE=CE=6,
∴AC=12.
∵△ABD的周长为24,
∴AB+BD+AC=AB+BD+CD=AB+BC=24,
∴△ABC的周长为:AB+BC+AC=36.
4.解:(1)在中,,,
∴.
又∵垂直平分,
∴,
∴,
∴.
(2)∵,∴,
∴.
答:的周长为19.
5.解:连接,.
是等腰三角形,点是边的中点,
,
,
解得,
是线段的垂直平分线,
点关于直线的对称点为点,,
,
的长为的最小值,
的周长最短.
故答案为:10.
6.解:(1)△EAF为直角三角形.
∵EM是AB的垂直平分线,
∴BE=AE,
∴∠BAE=∠B.
∵FN是AC的垂直平分线,
∴AF=CF,
∴∠CAF=∠C
.∵∠BAC=135°,
∴∠B+∠C=180°﹣∠BAC=180°﹣135°=45°,
∴∠BAE+∠CAF=45°,
∴∠EAF=135°﹣45°=90°,
∴△EAF为直角三角形;
(2)在△EAF中,
∵∠EAF=90°,
∴EF2=AE2+AF2,
∵BE=12,CF=9,
∴EF2=122+92=225,
∴EF=15,
∴△EAF的周长=12+9+15=36.
故答案为(1)△EAF为直角三角形.理由见解析;(2)△EAF的周长=36.
7.(1)解:根据轴对称图形的性质,
如图所示,即为所求:
.
(2)根据垂直平分线的性质,
作线段的垂直平分线,如图:
点、、、、都满足条件,
则网格中满足条件的点P共有5个,
故答案为:5.
(3)连接与直线交于点Q,
由轴对称图形的性质得,
,
则此时值最小,
如图所示,点Q即为所求:
8.(1)解:垂直平分
,
垂直平分
,
的周长
(2)在中,
,
,
垂直平分,
,
垂直平分,
,
,,
9.(1)解:是等边三角形,理由如下:
∵,
∴是等边三角形.
∴.
∵,
∴,
∴,
∴是等边三角形;
(2)解:连接交于点O,
∵,
∴是的垂直平分线,
即.
∵,
∴.
∵,
∴,
∴,
∴.
∵是等边三角形,
∴,
∴.
10.(1)证明:,
,
是的中点,
,
在与中,
,
,即点是的中点;
(2)解:,
,
又,,
是线段的垂直平分线,
,
,
.
11.(1)证明:如图,连接,
∵是边的垂直平分线,
∴.
∵,
∴,即.
∴是直角三角形.
∴;
(2)解:设,则,
∵,
∴.
∵,,
∴.
∴,
解得.
∴.
12.(1)解:∵点A在轴上,直线过点A,
∴点A坐标为
将点和点代入直线,得,
解得,
∴直线的函数表达式为;
(2)解:∵的垂直平分线交于点,
∴点的横坐标为,
将,代入,得,
∴点的坐标为;
(3)解:如图,设点坐标为,
在中,令得,
∴,
∵,,
∴,,,
∵点在线段上,,
∴,
解得:,
当时,,
∴点的坐标为.
13.(1)解: ,,
,
,
垂直平分,
,
,
故答案为:50;
(2)解:,
理由如下:∵,
∴,
∴,
∵,
∴;
(3)解:如图,
∵是线段的垂直平分线,
∴,
∴,
∵,,的周长是,
∴.
14.(1)解: ,
,
,
,
,
,
故答案为:;
(2)证明:如图,连接.
垂直平分线段,
,
.
,
,
,
,
由(1)知,
,
,
;
(3)解:垂直平分线段,
,
如图,过点作,交的延长线于点,则.
,
,
.
,
,
在和中,
,
,
,
,
,
.
15.(1)证明:如图,设与交与点G,
,于点D,
,
,,
,
;
(2)如图,连接,
,,
,
垂直平分,
,
,
,
,
,
,
,
;
(3)如图,连接,
,,
,
垂直平分,
,
,
平分,
,
,,
,
,
,
,
故答案为:.
16.(1)证明:∵,
∴,
又∵,,
∴,
∴,
又∵,
∴垂直平分;
(2)①证明:如图,
∵,
∴,
∴,
∵,
∴,
由(1)知,,
∴,,
∴,,
∵,
∴,
∴,
∵,
∴,
∴,
∴,
∴,
又∵,
∴是等边三角形;
②如图,延长至使得,则垂直平分线,
∴,
∴,
作于G,则此时取最小值,
∵是等边三角形,,
∴,
∴在中,.
17.解:(1)如图,延长,以点为圆心长为半径画弧,交延长线与点,连接,
∴即为所求;
(2)如图,同()作点关于对称点,连接
∴,
∵,,,
∴,
∴,
∵,,
∴是垂直平分线,
∴,
∴,
∴,
∴,
∵,,
∴;
(3),理由:
如图,
设,
∵,
∴,
在中,,
∵,
∴,
∴,
∴,
∵,
∴,
∵,
∴,
∵,,,
∴,
∴,
∴,
在中,
,
∴,
∴.
18.解:(1),,
,
,
,
,
∴,
∴,
是等腰三角形;
(2)过点D作,
,
,
∴,
,
是等腰三角形,
,
,
,
,
平分;
(3)由(2),
在中,,
在中,,
∴
,
∴,
∴
∴点在的垂直平分线上.
19.解:(1)∵,,
∴垂直平分,
∵,,
∴;
(2)图中的“筝形”有:四边形、四边形、四边形;
证明四边形是筝形:
由轴对称的性质可知,;
四边形是筝形.
同理:,;
四边形是筝形.
连接,
∵,,
∴,
∴,
∵,
∴,
∴,
∴,
∴四边形是筝形;
(3)证明:如图3中,
由轴对称的性质可知:
,,,,
∴,,
,
,
,
,
.
20.解:(1)如图1,延长至,使,连接,
∵为边上的中线,,,
∴,
在和中,
,
∴,
∴,
在中,根据三角形三边关系可得:,
即,
∵,
∴,
∴,
故答案为:,;
(2)如图2中,延长至点,使,连接,
∵点是的中点,
∴,
在和中,
,
∴,
∴,
∵,,
∴,
在中,由三角形的三边关系得:,
∴;
(3)结论:,,
如图3,延长于,使得,连接,延长交于,
∵点是的中点,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∵,
∴,
在和中,
,
∴,
∴,,
∵,,
∴,
∴,
∴,
即.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
