12.2.1三角形的内角教学设计
文档属性
| 名称 | 12.2.1三角形的内角教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 32.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-06-28 00:00:00 | ||
图片预览

文档简介
11.2.1 三角形的内角
【学习目标】
1、了解三角形的内角;
2、会用平行线的性质与平角的定义证明三角形内角和等于180度;
3、学会解决与求角有关的实际问题;
4、初步培养学生的说理能力。
【重点难点】
重点:了解三角形的内角和性质,学会解决简单的实际问题。
难点:说明三角形内角和等于180度。
【课型】 新授课
【学习方法】自学与小组合作学习相结合的方法
【教学用具】三角尺、铅画纸、小剪刀、量角器。电脑、投影仪
【学习过程】
一、动手操作,初步感知
问题:
1、三角形的内角和等于多少度?
2、在纸上画一个三角形将将它的内角剪下,试着拼拼看。
3、在同伴交流有哪些不同的拼合方法。
设计意图:从丰富的拼图活动中发展学思维的灵活性,创造性,为下一环节“说理”做准备。
二、实践说理,深入新知
问题:
1、由刚才拼合而成的图形,你能想出说明“三角形内角和等于180度"这个结论的正确方法吗?
2、把你的想法与同伴交流.
3、各小组派代表展示说理方法.
4、请同学们归纳上述各种不同的方法。
把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出
∠BCD的度数,可得到∠A+∠B+∠ACB=1800。[投影1]
( http: / / www.21cnjy.com )
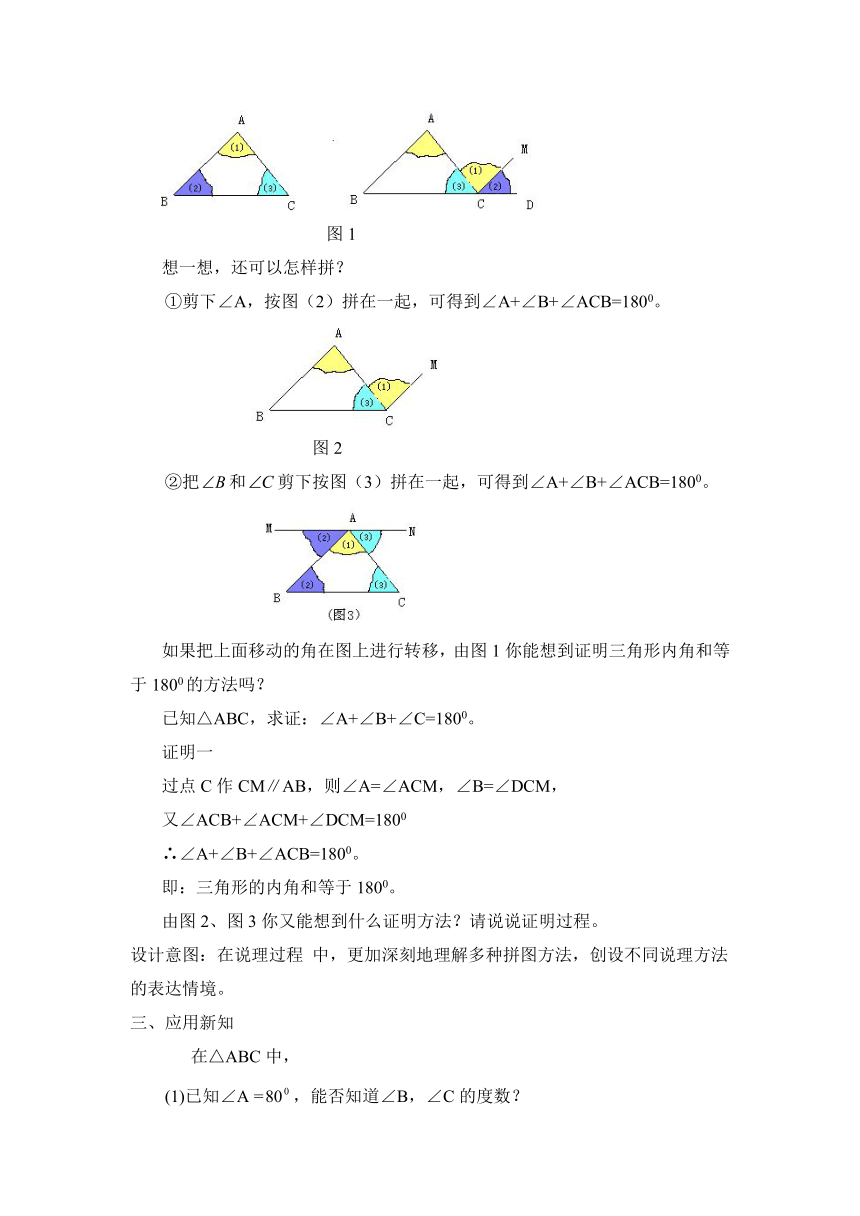
图1
想一想,还可以怎样拼?
①剪下∠A,按图(2)拼在一起,可得到∠A+∠B+∠ACB=1800。
( http: / / www.21cnjy.com )
图2
②把和剪下按图(3)拼在一起,可得到∠A+∠B+∠ACB=1800。
( http: / / www.21cnjy.com )
如果把上面移动的角在图上进行转移,由图1你能想到证明三角形内角和等于1800的方法吗?
已知△ABC,求证:∠A+∠B+∠C=1800。
证明一
过点C作CM∥AB,则∠A=∠ACM,∠B=∠DCM,
又∠ACB+∠ACM+∠DCM=1800
∴∠A+∠B+∠ACB=1800。
即:三角形的内角和等于1800。
由图2、图3你又能想到什么证明方法?请说说证明过程。
设计意图:在说理过程 中,更加深刻地理解多种拼图方法,创设不同说理方法的表达情境。
三、应用新知
在△ABC中,
(1)已知∠A =,能否知道∠B,∠C的度数?
(2)已知∠A =,∠B=,则∠C =
(3)已知∠A =,∠B-∠C=,则∠C
(4)已知∠A +∠B=,∠C =2∠A,能否求∠A、∠B、∠C的度数?
(5)已知∠A:∠B:∠C=1:3:5,能否求∠A、∠B、∠C的度数?
2、出示教科书12页例。
例1:如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线线.求∠ADB的度数.
例2:如图,C岛在A岛的北偏东50°方向 ( http: / / www.21cnjy.com ),B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
( http: / / www.21cnjy.com )
分析:怎样能求出∠ACB的度数?
设计3个问题:
请你解释一下这些方位角。
∠ACB是哪个三角形的内角?
有不同解法请你的同伴交流。
设计意图:向学生展示分析问题的基本方法,培养学生思维的广阔性。
根据三角形内角和定理,只需求出∠CAB和∠CBA的度数即可。
∠CAB等于多少度?怎样求∠CBA的度数?
解:∠CBA=∠BAD-∠CAD=80°-50°=30°
∵AD∥BE ∴∠BAD+∠ABE=180°
∴∠ABE=180°-∠BAD=180°-80°=100°
∴∠ABC=∠ABE-∠EBC=100°-40°=60°
∴∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°
答:从B岛看A,C两岛的视角∠ACB是90°,从C岛看A,B两岛的视角∠ACB是90°。
四、课堂练习
课本13面1、2题。
已知△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。
设计意图:增加第2小题,一方面巩固了前面的已学知识(高),另一方面进一步提高学生的说理能力。
五、总结归纳
采用让学生归纳、补充,然后教师补充的方式进行。
本节课我们学了什么知识?
你有什么收获?
设计意图:发挥学生主体意识,培养学生语言概括能力。
六、布置作业
必做题:教科书16页第1、3、4题。
选做题:
在∠C中,CD⊥AB,垂足是D,∠A=,∠BCD=,求∠B,∠ACB的度数。
在△ABC中,∠A+∠B=,∠C=2∠B,∠C=50°,分别求∠A、∠B的度数。
在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠BCD=27°,求∠ACD的度数,且探索∠BCD与∠A,∠B与∠ACD的关系。
将一个三角形纸片一刀分成两个三角形,能否这两个三角形:
都是直角三角形;
都是钝角三角形;
都是锐角三角形;
请简要说明理由。
A
B
C
D
【学习目标】
1、了解三角形的内角;
2、会用平行线的性质与平角的定义证明三角形内角和等于180度;
3、学会解决与求角有关的实际问题;
4、初步培养学生的说理能力。
【重点难点】
重点:了解三角形的内角和性质,学会解决简单的实际问题。
难点:说明三角形内角和等于180度。
【课型】 新授课
【学习方法】自学与小组合作学习相结合的方法
【教学用具】三角尺、铅画纸、小剪刀、量角器。电脑、投影仪
【学习过程】
一、动手操作,初步感知
问题:
1、三角形的内角和等于多少度?
2、在纸上画一个三角形将将它的内角剪下,试着拼拼看。
3、在同伴交流有哪些不同的拼合方法。
设计意图:从丰富的拼图活动中发展学思维的灵活性,创造性,为下一环节“说理”做准备。
二、实践说理,深入新知
问题:
1、由刚才拼合而成的图形,你能想出说明“三角形内角和等于180度"这个结论的正确方法吗?
2、把你的想法与同伴交流.
3、各小组派代表展示说理方法.
4、请同学们归纳上述各种不同的方法。
把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出
∠BCD的度数,可得到∠A+∠B+∠ACB=1800。[投影1]
( http: / / www.21cnjy.com )
图1
想一想,还可以怎样拼?
①剪下∠A,按图(2)拼在一起,可得到∠A+∠B+∠ACB=1800。
( http: / / www.21cnjy.com )
图2
②把和剪下按图(3)拼在一起,可得到∠A+∠B+∠ACB=1800。
( http: / / www.21cnjy.com )
如果把上面移动的角在图上进行转移,由图1你能想到证明三角形内角和等于1800的方法吗?
已知△ABC,求证:∠A+∠B+∠C=1800。
证明一
过点C作CM∥AB,则∠A=∠ACM,∠B=∠DCM,
又∠ACB+∠ACM+∠DCM=1800
∴∠A+∠B+∠ACB=1800。
即:三角形的内角和等于1800。
由图2、图3你又能想到什么证明方法?请说说证明过程。
设计意图:在说理过程 中,更加深刻地理解多种拼图方法,创设不同说理方法的表达情境。
三、应用新知
在△ABC中,
(1)已知∠A =,能否知道∠B,∠C的度数?
(2)已知∠A =,∠B=,则∠C =
(3)已知∠A =,∠B-∠C=,则∠C
(4)已知∠A +∠B=,∠C =2∠A,能否求∠A、∠B、∠C的度数?
(5)已知∠A:∠B:∠C=1:3:5,能否求∠A、∠B、∠C的度数?
2、出示教科书12页例。
例1:如图,在△ABC中,∠BAC=40°,∠B=75°,AD是△ABC的角平分线线.求∠ADB的度数.
例2:如图,C岛在A岛的北偏东50°方向 ( http: / / www.21cnjy.com ),B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向,从C岛看A、B两岛的视角∠ACB是多少度?
( http: / / www.21cnjy.com )
分析:怎样能求出∠ACB的度数?
设计3个问题:
请你解释一下这些方位角。
∠ACB是哪个三角形的内角?
有不同解法请你的同伴交流。
设计意图:向学生展示分析问题的基本方法,培养学生思维的广阔性。
根据三角形内角和定理,只需求出∠CAB和∠CBA的度数即可。
∠CAB等于多少度?怎样求∠CBA的度数?
解:∠CBA=∠BAD-∠CAD=80°-50°=30°
∵AD∥BE ∴∠BAD+∠ABE=180°
∴∠ABE=180°-∠BAD=180°-80°=100°
∴∠ABC=∠ABE-∠EBC=100°-40°=60°
∴∠ACB=180°-∠ABC-∠CAB=180°-60°-30°=90°
答:从B岛看A,C两岛的视角∠ACB是90°,从C岛看A,B两岛的视角∠ACB是90°。
四、课堂练习
课本13面1、2题。
已知△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数。
设计意图:增加第2小题,一方面巩固了前面的已学知识(高),另一方面进一步提高学生的说理能力。
五、总结归纳
采用让学生归纳、补充,然后教师补充的方式进行。
本节课我们学了什么知识?
你有什么收获?
设计意图:发挥学生主体意识,培养学生语言概括能力。
六、布置作业
必做题:教科书16页第1、3、4题。
选做题:
在∠C中,CD⊥AB,垂足是D,∠A=,∠BCD=,求∠B,∠ACB的度数。
在△ABC中,∠A+∠B=,∠C=2∠B,∠C=50°,分别求∠A、∠B的度数。
在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,∠BCD=27°,求∠ACD的度数,且探索∠BCD与∠A,∠B与∠ACD的关系。
将一个三角形纸片一刀分成两个三角形,能否这两个三角形:
都是直角三角形;
都是钝角三角形;
都是锐角三角形;
请简要说明理由。
A
B
C
D
