人教版数学九年级上册 24.1.3 弧、弦、圆心角 教案
文档属性
| 名称 | 人教版数学九年级上册 24.1.3 弧、弦、圆心角 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 57.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-19 16:55:52 | ||
图片预览

文档简介
24.1 圆的有关性质
24.1.3弧、弦、圆心角
【教学目标】
了解圆心角的概念:掌握在同圆或等圆中,圆心角、弦、弧中有一个量的两个相等就可以推出其它两个量的相对应的两个值就相等,及其它们在解题中的应用。
【教学重难点】
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对弦也相等及其两个推论和它们的应用。
2.探索定理和推导及其应用。
【教学过程】
一、复习引入。
(学生活动)请同学们完成下题。
已知△OAB,如图所示,作出绕O点旋转30°、45°、60°的图形。
老师点评:绕O点旋转,O点就是固定点,旋转30°,就是旋转角∠BOB′=30°。
二、探索新知。
如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫心角。
(学生活动)请同学们按下列要求作图并回答问题:
如图所示的⊙O中,分别作相等的圆心角∠AOB和∠A′OB′将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?
,AB=A′B′
理由:∵半径OA与O′A′重合,且∠AOB=∠A′OB′
∴半径OB与OB′重合
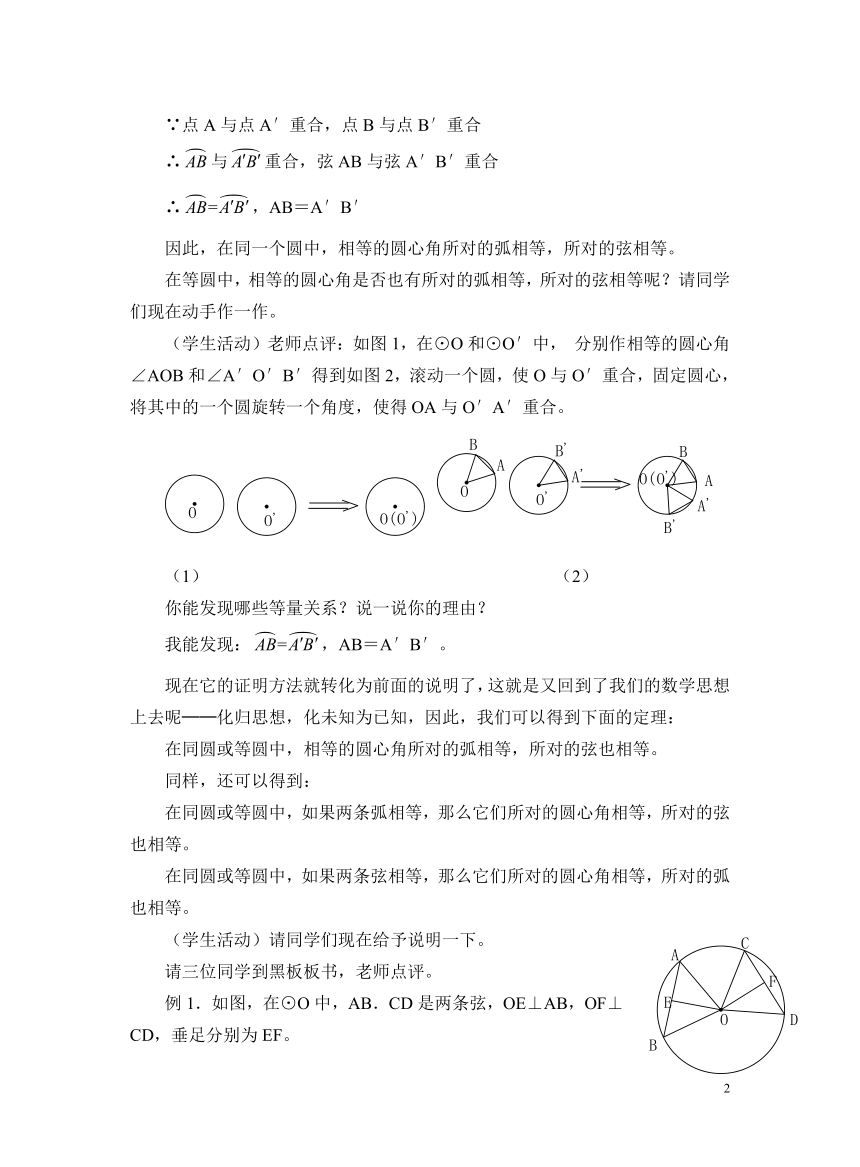
∵点A与点A′重合,点B与点B′重合
∴与重合,弦AB与弦A′B′重合
∴,AB=A′B′
因此,在同一个圆中,相等的圆心角所对的弧相等,所对的弦相等。
在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等呢?请同学们现在动手作一作。
(学生活动)老师点评:如图1,在⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,固定圆心,将其中的一个圆旋转一个角度,使得OA与O′A′重合。
(1) (2)
你能发现哪些等量关系?说一说你的理由?
我能发现:,AB=A′B′。
现在它的证明方法就转化为前面的说明了,这就是又回到了我们的数学思想上去呢──化归思想,化未知为已知,因此,我们可以得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等。
(学生活动)请同学们现在给予说明一下。
请三位同学到黑板板书,老师点评。
例1.如图,在⊙O中,AB.CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么与的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
分析:
(1)要说明OE=OF,只要在直角三角形AOE和直角三角形COF中说明AE=CF,即说明AB=CD,因此,只要运用前面所讲的定理即可。
(2)∵OE=OF,∴在Rt△AOE和Rt△COF中,
又有AO=CO是半径,∴Rt△AOE≌Rt△COF,
∴AE=CF,∴AB=CD,又可运用上面的定理得到。
三、巩固练习。
教材练习1。
四、应用拓展。
如图3和图4,MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM。
(1)由以上条件,你认为AB和CD大小关系是什么,请说明理由。
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由。
(3) (4)
分析:(1)要说明AB=CD,只要证明AB、CD所对的圆心角相等,只要说明它们的一半相等。
上述结论仍然成立,它的证明思路与上面的题目是一模一样的。
解:(1)AB=CD
理由:过O作OE、OF分别垂直于AB、CD,垂足分别为E、F
∵∠APM=∠CPM
∴∠1=∠2
OE=OF
连结OD、OB且OB=OD
∴Rt△OFD≌Rt△OEB
∴DF=BE
根据垂径定理可得:AB=CD
(2)作OE⊥AB,OF⊥CD,垂足为E、F
∵∠APM=∠CPN且OP=OP,∠PEO=∠PFO=90°
∴Rt△OPE≌Rt△OPF
∴OE=OF
连接OA、OB、OC、OD易证Rt△OBE≌Rt△ODF,Rt△OAE≌Rt△OCF
∴∠1+∠2=∠3+∠4
∴AB=CD
五、归纳总结(学生归纳,老师点评)。
1.圆心角概念。
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都部分相等,及其它们的应用。
1
24.1.3弧、弦、圆心角
【教学目标】
了解圆心角的概念:掌握在同圆或等圆中,圆心角、弦、弧中有一个量的两个相等就可以推出其它两个量的相对应的两个值就相等,及其它们在解题中的应用。
【教学重难点】
1.在同圆或等圆中,相等的圆心角所对的弧相等,所对弦也相等及其两个推论和它们的应用。
2.探索定理和推导及其应用。
【教学过程】
一、复习引入。
(学生活动)请同学们完成下题。
已知△OAB,如图所示,作出绕O点旋转30°、45°、60°的图形。
老师点评:绕O点旋转,O点就是固定点,旋转30°,就是旋转角∠BOB′=30°。
二、探索新知。
如图所示,∠AOB的顶点在圆心,像这样顶点在圆心的角叫心角。
(学生活动)请同学们按下列要求作图并回答问题:
如图所示的⊙O中,分别作相等的圆心角∠AOB和∠A′OB′将圆心角∠AOB绕圆心O旋转到∠A′OB′的位置,你能发现哪些等量关系?为什么?
,AB=A′B′
理由:∵半径OA与O′A′重合,且∠AOB=∠A′OB′
∴半径OB与OB′重合
∵点A与点A′重合,点B与点B′重合
∴与重合,弦AB与弦A′B′重合
∴,AB=A′B′
因此,在同一个圆中,相等的圆心角所对的弧相等,所对的弦相等。
在等圆中,相等的圆心角是否也有所对的弧相等,所对的弦相等呢?请同学们现在动手作一作。
(学生活动)老师点评:如图1,在⊙O和⊙O′中,分别作相等的圆心角∠AOB和∠A′O′B′得到如图2,滚动一个圆,使O与O′重合,固定圆心,将其中的一个圆旋转一个角度,使得OA与O′A′重合。
(1) (2)
你能发现哪些等量关系?说一说你的理由?
我能发现:,AB=A′B′。
现在它的证明方法就转化为前面的说明了,这就是又回到了我们的数学思想上去呢──化归思想,化未知为已知,因此,我们可以得到下面的定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
同样,还可以得到:
在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角相等,所对的弦也相等。
在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角相等,所对的弧也相等。
(学生活动)请同学们现在给予说明一下。
请三位同学到黑板板书,老师点评。
例1.如图,在⊙O中,AB.CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为EF。
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么与的大小有什么关系?AB与CD的大小有什么关系?为什么?∠AOB与∠COD呢?
分析:
(1)要说明OE=OF,只要在直角三角形AOE和直角三角形COF中说明AE=CF,即说明AB=CD,因此,只要运用前面所讲的定理即可。
(2)∵OE=OF,∴在Rt△AOE和Rt△COF中,
又有AO=CO是半径,∴Rt△AOE≌Rt△COF,
∴AE=CF,∴AB=CD,又可运用上面的定理得到。
三、巩固练习。
教材练习1。
四、应用拓展。
如图3和图4,MN是⊙O的直径,弦AB、CD相交于MN上的一点P,∠APM=∠CPM。
(1)由以上条件,你认为AB和CD大小关系是什么,请说明理由。
(2)若交点P在⊙O的外部,上述结论是否成立?若成立,加以证明;若不成立,请说明理由。
(3) (4)
分析:(1)要说明AB=CD,只要证明AB、CD所对的圆心角相等,只要说明它们的一半相等。
上述结论仍然成立,它的证明思路与上面的题目是一模一样的。
解:(1)AB=CD
理由:过O作OE、OF分别垂直于AB、CD,垂足分别为E、F
∵∠APM=∠CPM
∴∠1=∠2
OE=OF
连结OD、OB且OB=OD
∴Rt△OFD≌Rt△OEB
∴DF=BE
根据垂径定理可得:AB=CD
(2)作OE⊥AB,OF⊥CD,垂足为E、F
∵∠APM=∠CPN且OP=OP,∠PEO=∠PFO=90°
∴Rt△OPE≌Rt△OPF
∴OE=OF
连接OA、OB、OC、OD易证Rt△OBE≌Rt△ODF,Rt△OAE≌Rt△OCF
∴∠1+∠2=∠3+∠4
∴AB=CD
五、归纳总结(学生归纳,老师点评)。
1.圆心角概念。
2.在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都部分相等,及其它们的应用。
1
同课章节目录
