【新课堂】华师版数学九年级下册 26.2.1 二次函数y=ax2的图象和性质 课件(共23张PPT)
文档属性
| 名称 | 【新课堂】华师版数学九年级下册 26.2.1 二次函数y=ax2的图象和性质 课件(共23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 15:00:10 | ||
图片预览






文档简介
(共23张PPT)
华师大版数学
九年级下册
1.亲爱的同学们,上节课我们学习了二次函数的定义,什么是二次函数呢?
2.在研究一次函数时,曾借助图象了解了一次函数的性质.怎样画函数的图象呢?
新知讲解
我们知道,一次函数的图象是一条直线.那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?
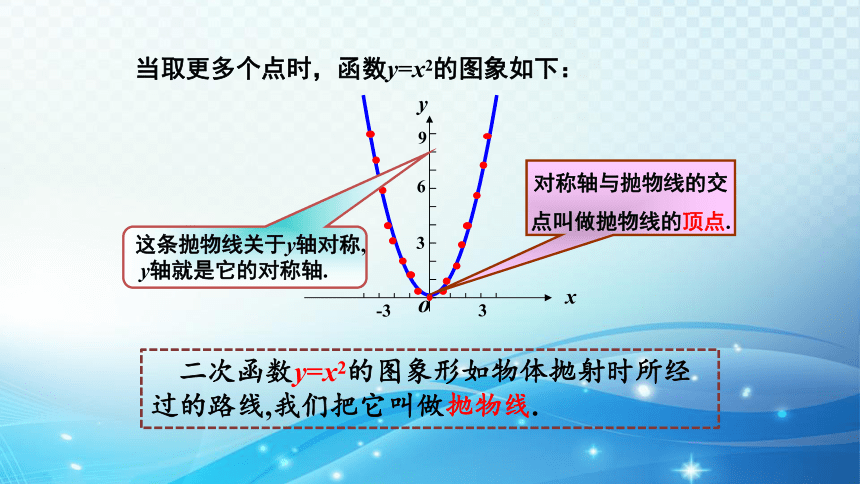
这样的曲线通常叫做抛物线.它是轴对称图形,y轴是它的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点.
二次函数y=ax2的图象
典例精析
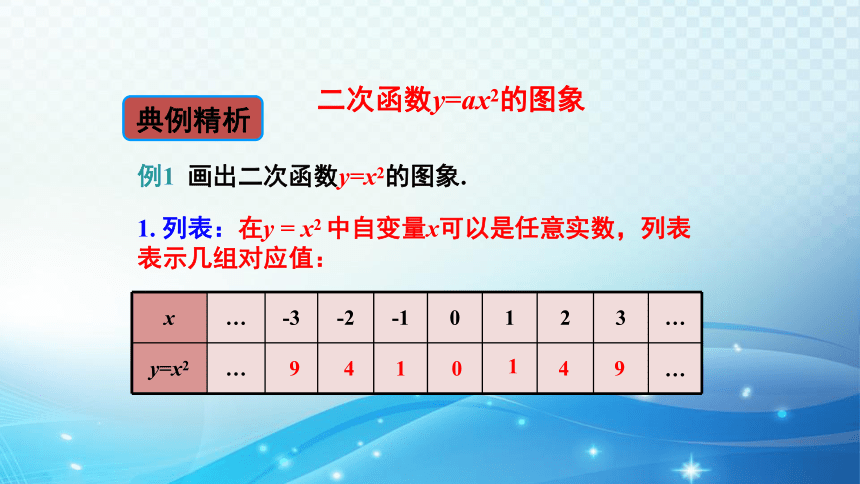
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
例1 画出二次函数y=x2的图象.
9
4
1
0
1
9
4
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
2
4
-2
-4
o
3
6
9
x
y
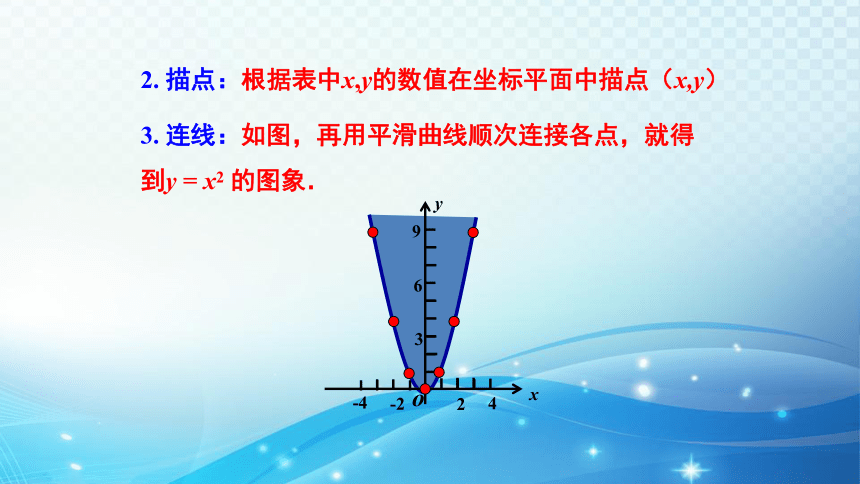
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图象.
-3
3
o
3
6
9
当取更多个点时,函数y=x2的图象如下:
x
y
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,
y轴就是它的对称轴.
对称轴与抛物线的交
点叫做抛物线的顶点.
(1)在同一个平面直角坐标系中,画出函数y=x2与y=-x2的图象,观察并比较这两个函数的图象,它们有什么共同点?又有什么区别?
(2)在同一个平面直角坐标系中,画出函数y=2x2与y=-2x2的图象,观察并比较这两个函数的图象,你能发现什么?
(3)将所画的四个函数的图象作比较,你又能发现什么?
做一做
(1)在同一个平面直角坐标系中,画出函数y=x2与y=-x2的图象.
x
y=x2
0
1
2
3
…
-1
-2
-3
…
0
1
4
9
…
1
4
9
…
x
y=-x2
0
1
2
3
…
-1
-2
-3
…
0
-1
-4
-9
…
-1
-4
-9
…
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
-10
-8
-6
-4
y=x2
y=-x2
描点
连线
(2)在同一个平面直角坐标系中,画出函数y=2x2与y=-2x2的图象.
x
y=2x2
0
1
2
3
…
-1
-2
-3
…
0
2
8
18
…
2
8
18
…
x
y=-2x2
0
1
2
3
…
-1
-2
-3
…
0
-2
-8
-18
…
-2
-8
-18
…
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
20
16
12
8
4
-4
-20
-16
-12
-8
描点
连线
y=2x2
y=-2x2
函数y=ax2(a≠0)的图象是一条抛物线,它关于y轴对称,顶点坐标是(0,0).
同学们,观察y=x2和y=2x2的图象,可以看出什么特点呢?
若a>0时,抛物线y=ax2开口向上,在对称轴的左边,曲线自左向右下降;在对称轴的右边,曲线自左向右上升.顶点是抛物线上位置最低的点.
图象的这些特点反映了函数的什么性质?
图象的这些特点表明,函数y=ax2 (a>0)具有这样的性质:当x<0时,函数值y随着x的增大而减小;
当x>0时,函数值y随着x的增大而增大;
当x=0时,函数y=ax2取得最小值,最小值y=0.
观察函数y=-x2和y=-2x2图象,试作出类似的概括,即思考:若a<0,抛物线 y=ax2有什么特点?它反映了函数y=ax2 (a<0)具有哪些性质
抛物线 y=ax2 (a<0)的特点
若a<0时,抛物线y=ax2开口向下,在对称轴的左边,曲线自左向右上升;在对称轴的右边,曲线自左向右下降.顶点是抛物线上位置最高的点.
函数y=ax2 (a<0)的性质
当x<0时,函数值y随着x的增大而增大;
当x>0时,函数值y随着x的增大而减小;
当x=0时,函数y=ax2取得最大值,最大值y=0.
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2
y= -ax2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
填空:
(1)抛物线y=-9x2的顶点坐标是___________;对称轴是________;
在_____________ 侧,y随着x的增大而增大;
在______________侧,y随着x的增大而减小;
当x=_______时,函数y的值最大,最大值是________;
抛物线y=-9x2在x轴的________方(除顶点外).
(0,0)
y轴
对称轴的左
0
对称轴的右
0
下
巩固练习
解:
∵抛物线y=ax2与反比例函数 的图象交于一点,
∴ax2 ,
∵ 交点横坐标大于0,∴
解得:a<0
课堂总结
通过本节课你学到了什么?
图象
性质
二次函数
列表—描点—连线
华师大版数学
九年级下册
1.亲爱的同学们,上节课我们学习了二次函数的定义,什么是二次函数呢?
2.在研究一次函数时,曾借助图象了解了一次函数的性质.怎样画函数的图象呢?
新知讲解
我们知道,一次函数的图象是一条直线.那么,二次函数的图象是什么?它有什么特点?反映了二次函数的哪些性质?
这样的曲线通常叫做抛物线.它是轴对称图形,y轴是它的对称轴,抛物线与它的对称轴的交点叫做抛物线的顶点.
二次函数y=ax2的图象
典例精析
x … -3 -2 -1 0 1 2 3 …
y=x2 … …
例1 画出二次函数y=x2的图象.
9
4
1
0
1
9
4
1. 列表:在y = x2 中自变量x可以是任意实数,列表表示几组对应值:
2
4
-2
-4
o
3
6
9
x
y
2. 描点:根据表中x,y的数值在坐标平面中描点(x,y)
3. 连线:如图,再用平滑曲线顺次连接各点,就得到y = x2 的图象.
-3
3
o
3
6
9
当取更多个点时,函数y=x2的图象如下:
x
y
二次函数y=x2的图象形如物体抛射时所经过的路线,我们把它叫做抛物线.
这条抛物线关于y轴对称,
y轴就是它的对称轴.
对称轴与抛物线的交
点叫做抛物线的顶点.
(1)在同一个平面直角坐标系中,画出函数y=x2与y=-x2的图象,观察并比较这两个函数的图象,它们有什么共同点?又有什么区别?
(2)在同一个平面直角坐标系中,画出函数y=2x2与y=-2x2的图象,观察并比较这两个函数的图象,你能发现什么?
(3)将所画的四个函数的图象作比较,你又能发现什么?
做一做
(1)在同一个平面直角坐标系中,画出函数y=x2与y=-x2的图象.
x
y=x2
0
1
2
3
…
-1
-2
-3
…
0
1
4
9
…
1
4
9
…
x
y=-x2
0
1
2
3
…
-1
-2
-3
…
0
-1
-4
-9
…
-1
-4
-9
…
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
-10
-8
-6
-4
y=x2
y=-x2
描点
连线
(2)在同一个平面直角坐标系中,画出函数y=2x2与y=-2x2的图象.
x
y=2x2
0
1
2
3
…
-1
-2
-3
…
0
2
8
18
…
2
8
18
…
x
y=-2x2
0
1
2
3
…
-1
-2
-3
…
0
-2
-8
-18
…
-2
-8
-18
…
列表
x
y
0
-4
-3
-2
-1
1
2
3
4
20
16
12
8
4
-4
-20
-16
-12
-8
描点
连线
y=2x2
y=-2x2
函数y=ax2(a≠0)的图象是一条抛物线,它关于y轴对称,顶点坐标是(0,0).
同学们,观察y=x2和y=2x2的图象,可以看出什么特点呢?
若a>0时,抛物线y=ax2开口向上,在对称轴的左边,曲线自左向右下降;在对称轴的右边,曲线自左向右上升.顶点是抛物线上位置最低的点.
图象的这些特点反映了函数的什么性质?
图象的这些特点表明,函数y=ax2 (a>0)具有这样的性质:当x<0时,函数值y随着x的增大而减小;
当x>0时,函数值y随着x的增大而增大;
当x=0时,函数y=ax2取得最小值,最小值y=0.
观察函数y=-x2和y=-2x2图象,试作出类似的概括,即思考:若a<0,抛物线 y=ax2有什么特点?它反映了函数y=ax2 (a<0)具有哪些性质
抛物线 y=ax2 (a<0)的特点
若a<0时,抛物线y=ax2开口向下,在对称轴的左边,曲线自左向右上升;在对称轴的右边,曲线自左向右下降.顶点是抛物线上位置最高的点.
函数y=ax2 (a<0)的性质
当x<0时,函数值y随着x的增大而增大;
当x>0时,函数值y随着x的增大而减小;
当x=0时,函数y=ax2取得最大值,最大值y=0.
抛物线
顶点坐标
对称轴
位置
开口方向
增减性
最值
y=ax2
y= -ax2
(0,0)
(0,0)
y轴
y轴
在x轴的上方(除顶点外)
在x轴的下方( 除顶点外)
向上
向下
当x=0时,最小值为0.
当x=0时,最大值为0.
在对称轴的左侧,y随着x的增大而减小. 在对称轴的右侧, y随着x的增大而增大.
在对称轴的左侧,y随着x的增大而增大. 在对称轴的右侧, y随着x的增大而减小.
填空:
(1)抛物线y=-9x2的顶点坐标是___________;对称轴是________;
在_____________ 侧,y随着x的增大而增大;
在______________侧,y随着x的增大而减小;
当x=_______时,函数y的值最大,最大值是________;
抛物线y=-9x2在x轴的________方(除顶点外).
(0,0)
y轴
对称轴的左
0
对称轴的右
0
下
巩固练习
解:
∵抛物线y=ax2与反比例函数 的图象交于一点,
∴ax2 ,
∵ 交点横坐标大于0,∴
解得:a<0
课堂总结
通过本节课你学到了什么?
图象
性质
二次函数
列表—描点—连线
