七年级数学下册试题 10.5用二元一次方程组解决问题--表格信息问题-苏科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 10.5用二元一次方程组解决问题--表格信息问题-苏科版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 18:16:21 | ||
图片预览




文档简介
10.5用二元一次方程组解决问题--表格信息问题
一、选择题.
1.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2 B.4 C.﹣6 D.6
2.如图,已知表格中竖直、水平、对角线上的三个数的和都相等,则m+n等于( )
m ﹣3 4
3 1
n
A.7 B.5 C.﹣1 D.﹣2
3.某校七年级(1)班同学为“希望工程”捐款,共捐款206元,捐款情况如下表所示:
由于不小心被墨水污染,表格中捐款4元和5元的人数已经看不清楚,根据已有的信息推断,捐款4元和5元的人数不可能为( )
A.6,24 B.8,22 C.11,20 D.16,16
4.工作人员从仓库领取如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
下表是工作人员四次领取纸板数的记录:
日期 正方形纸板(张) 长方形纸板(张)
第一次 562 938
第二次 420 860
第三次 502 1000
第四次 985 2015
仓库管理员在核查时,发现一次记录有误.请问记录有误的是( )
A.第一次 B.第二次 C.第三次 D.第四次
5.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
6.为奖励校学养节表现优异的同学,张老师打算买8支单价相同的钢笔和6本单价相同的笔记本作为奖励,她与售货员的对话如下,则买一支钢笔和一本笔记本应付( )
老师:您好,我要买8支钢笔和6本笔记本. 售货员:好的,那您应付款l90元. 老师:刚才我把两种文具的单价弄反了,以为要付160元.
A.22元 B.25元 C.27元 D.30元
7.踩高跷又称为“扎高脚”“缚柴脚”,如图是一位演员踩着长度为身高一半的高跷,脚踏处距高跷顶端,演员踩在高跷上时,“身高”为.设演员的身高为,高跷的长度为,则下列方程组正确的是( )
A. B.
C. D.
8.滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 里程费 时长费 远途费
单价 1.8元每公里 0.45元每分钟 0.4元每公里
注:车费由里程费、时长费、远途费三部分组成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元.
小明和小亮在17:00-18:30之间各自乘坐滴滴快车回家,行车里程分别为9.5公里与14.5公里.如果下车时两人所付车费相同,问这两辆滴滴快车的行车时间相差( )分钟.
A.14 B.20 C.24 D.30
9.如图,我们可以按竖放、平放两种方式在同一个书架上摆放一定数量的同一本书,并且要求书脊朝外,方便我们查阅.根据图中的数据,可计算:若只按某一种方式摆放,该书架上最多可摆放这本书的数量为()
A.36本 B.38本 C.40本 D.42本
10.如图,由组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行(横) 每一列(竖)以及每一条对角线(斜)上的三个代数式的和均相等,则方格中“a”的数是( )
y a
9 11
A.6 B.7 C.8 D.9
二、 填空题
11.某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
捐款(元) 1 2 3 4
人 数 6 7
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组___________________.
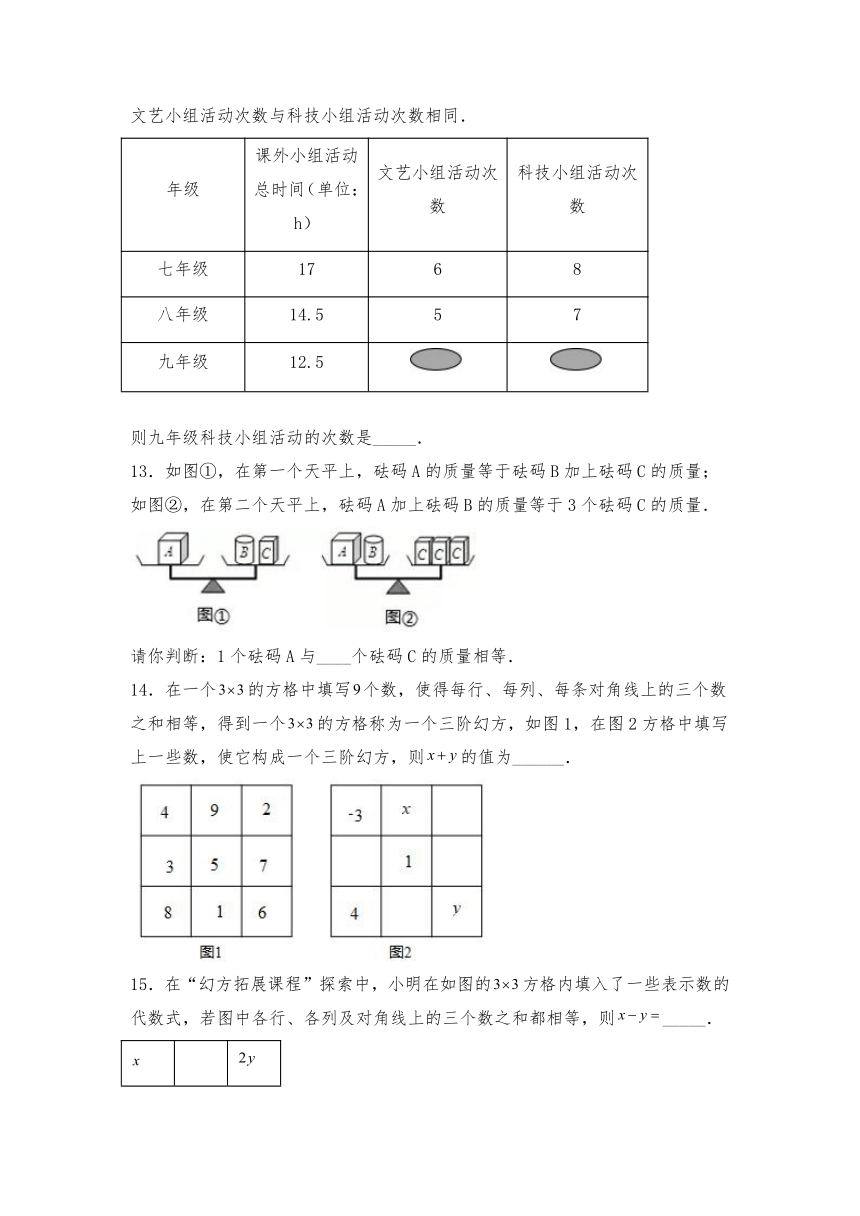
12.下表是某校七﹣九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,但表格中九年级的两个数据被遮盖了,记得九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 17 6 8
八年级 14.5 5 7
九年级 12.5
则九年级科技小组活动的次数是_____.
13.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;
如图②,在第二个天平上,砝码A加上砝码B的质量等于3个砝码C的质量.
请你判断:1个砝码A与____个砝码C的质量相等.
14.在一个的方格中填写个数,使得每行、每列、每条对角线上的三个数之和相等,得到一个的方格称为一个三阶幻方,如图1,在图2方格中填写上一些数,使它构成一个三阶幻方,则的值为______.
15.在“幻方拓展课程”探索中,小明在如图的方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则_____.
-2 6
0
16.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投进几个球的人数分布情况,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,则投进3个球的、投进4个球的依次有______人.
进球数n(个) 0 1 2 3 4 5
投进n个球的人数 1 2 7 2
17.某纸厂要制作如图的甲、乙两种无盖的小长方体盒子.该厂利用边角材料裁出了长方形和正方形两种纸片,其中长方形纸片的宽和正方形纸片的边长相等.现用150张正方形纸片和300张长方形纸片制作这两种小盒,恰好用完.设可做成甲、乙两种盒子各x、y个,根据题意,可列正确的方程组为 __.
18.在3×3的方格内,填入一些代数式与数,若各行、各列及对角线上的三个数字之和都相等.则_______;_______.
3 2
y
三、解答题
19.为了增强公民的节水意识,合理利用水资源,某市出台了居民用水“阶梯价格”制度来引导市民节约用水,下表是用水价格的标准:
阶梯 一户居民每月用水量(单位:立方米) 水费价格(单位:元/立方米)
一档 不超过15立方米 a
二档 超过15立方米的部分 b
已知该市某户居民今年4月份用水16立方米,缴纳水费50元;5月份用水20立方米,缴纳水费70元.
(1)求出表格中a、b的值;
(2)6月份是用水高峰期,该户居民计划6月份水费支出不超过85元,那么该户居民6月份最多可用水多少立方米?
20.为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 1~50人 50~100人 100以上人
每套服装价格/元 50 45 40
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
21.某商店销售甲、乙两种商品.现有如下信息:
(1)请设计一张表格,并把上述信息中的已知数量填进去;
(2)根据情境中的信息,提出一个问题,并用二元一次方程组解决这个问题.
22.某代驾公司规定:代驾服务在21:00-23:59的起步价允许行驶的最远路程为5千米,超过5千米的部分按每千米另行收费,不足1千米按照1千米计算,下面是两个朋友的对话.
根据对话内容,请你用方程的知识求出代驾服务在21:00-23:59的起步价是多少元,以及超过5千米后每千米是如何收费的?
23.如图在3×3的方阵图中,填写了一些数和代数式 (其中每个代数式都表示一个数),使得每行的3个数,每列的3个数,斜对角的3个数之和均相等
(1)求x,y的值
(2)重新作图完成此方阵图
24.上学期,我们学习了解一元一次方程及用一元一次方程解决实际问题.本学期,我们又学习了解二元一次方程组,试用二元一次方程组及以前解决实际问题的经验解决下列问题:
某校初一(1)班45名同学为“支援灾区”共捐款900元,捐款情况如下表:
捐款(元) 5 10 20 50
人数 6 7
表中捐款10元和20元的人数不小心被墨水污染,看不清楚,请你确定表中的数据.
答案
一、选择题.
C.A.B.C.C.B.A.C.C.B.
二、填空题
11.
12.5.
13.2
14.13
15.6
16.9,3
17..
18. -1 1
三、解答题
19.
解:(1)设该市居民用水基本价格为a元/米3,超过15米3部分的价格为b元/米3,
根据题意,得,
解得:.
答:a的值是3,b的值是5.
(2)设该户居民6月份最多可用水x立方米,
根据题意,得15×3+5(x-15)≤85.
解得x≤23.
答:该户居民6月份最多可用水23立方米.
20.
(1)设(15)班有名学生,(16)班有名学生,
∵103×45=4635(元),4635<4875,
∴.
依题意,得:,
解得:.
答:(15)班有55名学生,(16)班有48名学生;
(2)4875-40×103=755(元).
答:如果两个班联合起来,做为一个整体购买,则能节省755元钱.
21.
解:
(1)可设计如下表格.
销售单价(元/件) 数量(件) 金额(元)
甲商品 3
乙商品 2
合计 5 12
(2)答案不唯一,例如,甲、乙两种商品零售单价分别是多少元?
设甲商品零售单价为元/件,乙商品零售单价为元/件.
根据题意,得,
解得 ;
答:甲商品零售单价是每件2元,乙商品零售单价是每件3元.
22.
解:设代驾服务在21:00-23:59的起步价是x元,超过5千米后每千米的收费为y元,
根据题意,得
解得
答:代驾服务在21:00-23:59的起步价是18元,超过5千米后每千米的收费为6元.
23.
解:(1)由题意,得
解得
(2)如图
24.设捐款10元的x人,捐款20元的y人,根据“45名同学共捐款900元”即可列方程组求解.
设捐款10元的x人,捐款20元的y人,由题意得
解得
答:捐款10元的12人,捐款20元的20人.
一、选择题.
1.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y﹣x=( )
A.2 B.4 C.﹣6 D.6
2.如图,已知表格中竖直、水平、对角线上的三个数的和都相等,则m+n等于( )
m ﹣3 4
3 1
n
A.7 B.5 C.﹣1 D.﹣2
3.某校七年级(1)班同学为“希望工程”捐款,共捐款206元,捐款情况如下表所示:
由于不小心被墨水污染,表格中捐款4元和5元的人数已经看不清楚,根据已有的信息推断,捐款4元和5元的人数不可能为( )
A.6,24 B.8,22 C.11,20 D.16,16
4.工作人员从仓库领取如图①中的长方形和正方形纸板作侧面和底面,做成如图②的竖式和横式的两种无盖纸盒若干个,恰好使领取的纸板用完.
下表是工作人员四次领取纸板数的记录:
日期 正方形纸板(张) 长方形纸板(张)
第一次 562 938
第二次 420 860
第三次 502 1000
第四次 985 2015
仓库管理员在核查时,发现一次记录有误.请问记录有误的是( )
A.第一次 B.第二次 C.第三次 D.第四次
5.如图1是2021年3月份的月历,小军同学用“”字形框在月历上框出四个数字,将该“”字形框上下左右移动,且一定要框住月历中的四个日期,若四个日期如图2所示,则下列关于m,n的值分别为( )
A.m=4,n=4 B.m=8,n=4 C.m=4,n=12 D.m=12,n=4
6.为奖励校学养节表现优异的同学,张老师打算买8支单价相同的钢笔和6本单价相同的笔记本作为奖励,她与售货员的对话如下,则买一支钢笔和一本笔记本应付( )
老师:您好,我要买8支钢笔和6本笔记本. 售货员:好的,那您应付款l90元. 老师:刚才我把两种文具的单价弄反了,以为要付160元.
A.22元 B.25元 C.27元 D.30元
7.踩高跷又称为“扎高脚”“缚柴脚”,如图是一位演员踩着长度为身高一半的高跷,脚踏处距高跷顶端,演员踩在高跷上时,“身高”为.设演员的身高为,高跷的长度为,则下列方程组正确的是( )
A. B.
C. D.
8.滴滴快车是一种便捷的出行工具,计价规则如下表:
计费项目 里程费 时长费 远途费
单价 1.8元每公里 0.45元每分钟 0.4元每公里
注:车费由里程费、时长费、远途费三部分组成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车10公里以内(含10公里)不收远途费,超过10公里的,超出部分每公里收0.4元.
小明和小亮在17:00-18:30之间各自乘坐滴滴快车回家,行车里程分别为9.5公里与14.5公里.如果下车时两人所付车费相同,问这两辆滴滴快车的行车时间相差( )分钟.
A.14 B.20 C.24 D.30
9.如图,我们可以按竖放、平放两种方式在同一个书架上摆放一定数量的同一本书,并且要求书脊朝外,方便我们查阅.根据图中的数据,可计算:若只按某一种方式摆放,该书架上最多可摆放这本书的数量为()
A.36本 B.38本 C.40本 D.42本
10.如图,由组成的方格中每个方格内均有代数式(图中只列出了部分代数式),方格中每一行(横) 每一列(竖)以及每一条对角线(斜)上的三个代数式的和均相等,则方格中“a”的数是( )
y a
9 11
A.6 B.7 C.8 D.9
二、 填空题
11.某校初三(2)班40名同学为“希望工程”捐款,共捐款100元.捐款情况如下表:
捐款(元) 1 2 3 4
人 数 6 7
表格中捐款2元和3元的人数不小心被墨水污染已看不清楚.若设捐款2元的有x名同学,捐款3元的有y名同学,根据题意,可得方程组___________________.
12.下表是某校七﹣九年级某月课外兴趣小组活动时间统计表,其中各年级同一兴趣小组每次活动时间相同,但表格中九年级的两个数据被遮盖了,记得九年级文艺小组活动次数与科技小组活动次数相同.
年级 课外小组活动总时间(单位:h) 文艺小组活动次数 科技小组活动次数
七年级 17 6 8
八年级 14.5 5 7
九年级 12.5
则九年级科技小组活动的次数是_____.
13.如图①,在第一个天平上,砝码A的质量等于砝码B加上砝码C的质量;
如图②,在第二个天平上,砝码A加上砝码B的质量等于3个砝码C的质量.
请你判断:1个砝码A与____个砝码C的质量相等.
14.在一个的方格中填写个数,使得每行、每列、每条对角线上的三个数之和相等,得到一个的方格称为一个三阶幻方,如图1,在图2方格中填写上一些数,使它构成一个三阶幻方,则的值为______.
15.在“幻方拓展课程”探索中,小明在如图的方格内填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则_____.
-2 6
0
16.某班进行个人投篮比赛,受污损的下表记录了在规定时间内投进几个球的人数分布情况,已知进球3个或3个以上的人平均每人投进3.5个球,进球4个或4个以下的人平均每人投进2.5个球,则投进3个球的、投进4个球的依次有______人.
进球数n(个) 0 1 2 3 4 5
投进n个球的人数 1 2 7 2
17.某纸厂要制作如图的甲、乙两种无盖的小长方体盒子.该厂利用边角材料裁出了长方形和正方形两种纸片,其中长方形纸片的宽和正方形纸片的边长相等.现用150张正方形纸片和300张长方形纸片制作这两种小盒,恰好用完.设可做成甲、乙两种盒子各x、y个,根据题意,可列正确的方程组为 __.
18.在3×3的方格内,填入一些代数式与数,若各行、各列及对角线上的三个数字之和都相等.则_______;_______.
3 2
y
三、解答题
19.为了增强公民的节水意识,合理利用水资源,某市出台了居民用水“阶梯价格”制度来引导市民节约用水,下表是用水价格的标准:
阶梯 一户居民每月用水量(单位:立方米) 水费价格(单位:元/立方米)
一档 不超过15立方米 a
二档 超过15立方米的部分 b
已知该市某户居民今年4月份用水16立方米,缴纳水费50元;5月份用水20立方米,缴纳水费70元.
(1)求出表格中a、b的值;
(2)6月份是用水高峰期,该户居民计划6月份水费支出不超过85元,那么该户居民6月份最多可用水多少立方米?
20.为迎接济川中学红歌演讲比赛,济川校区七年级(15)(16)班决定订购同一套服装,两班一共有103人(15班人数多于16班),经协商,某服装店给出的价格如下:
购买人数/人 1~50人 50~100人 100以上人
每套服装价格/元 50 45 40
例如:若购买人数为60人,则购买共需花费60×45=2700元.
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么15,16班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
21.某商店销售甲、乙两种商品.现有如下信息:
(1)请设计一张表格,并把上述信息中的已知数量填进去;
(2)根据情境中的信息,提出一个问题,并用二元一次方程组解决这个问题.
22.某代驾公司规定:代驾服务在21:00-23:59的起步价允许行驶的最远路程为5千米,超过5千米的部分按每千米另行收费,不足1千米按照1千米计算,下面是两个朋友的对话.
根据对话内容,请你用方程的知识求出代驾服务在21:00-23:59的起步价是多少元,以及超过5千米后每千米是如何收费的?
23.如图在3×3的方阵图中,填写了一些数和代数式 (其中每个代数式都表示一个数),使得每行的3个数,每列的3个数,斜对角的3个数之和均相等
(1)求x,y的值
(2)重新作图完成此方阵图
24.上学期,我们学习了解一元一次方程及用一元一次方程解决实际问题.本学期,我们又学习了解二元一次方程组,试用二元一次方程组及以前解决实际问题的经验解决下列问题:
某校初一(1)班45名同学为“支援灾区”共捐款900元,捐款情况如下表:
捐款(元) 5 10 20 50
人数 6 7
表中捐款10元和20元的人数不小心被墨水污染,看不清楚,请你确定表中的数据.
答案
一、选择题.
C.A.B.C.C.B.A.C.C.B.
二、填空题
11.
12.5.
13.2
14.13
15.6
16.9,3
17..
18. -1 1
三、解答题
19.
解:(1)设该市居民用水基本价格为a元/米3,超过15米3部分的价格为b元/米3,
根据题意,得,
解得:.
答:a的值是3,b的值是5.
(2)设该户居民6月份最多可用水x立方米,
根据题意,得15×3+5(x-15)≤85.
解得x≤23.
答:该户居民6月份最多可用水23立方米.
20.
(1)设(15)班有名学生,(16)班有名学生,
∵103×45=4635(元),4635<4875,
∴.
依题意,得:,
解得:.
答:(15)班有55名学生,(16)班有48名学生;
(2)4875-40×103=755(元).
答:如果两个班联合起来,做为一个整体购买,则能节省755元钱.
21.
解:
(1)可设计如下表格.
销售单价(元/件) 数量(件) 金额(元)
甲商品 3
乙商品 2
合计 5 12
(2)答案不唯一,例如,甲、乙两种商品零售单价分别是多少元?
设甲商品零售单价为元/件,乙商品零售单价为元/件.
根据题意,得,
解得 ;
答:甲商品零售单价是每件2元,乙商品零售单价是每件3元.
22.
解:设代驾服务在21:00-23:59的起步价是x元,超过5千米后每千米的收费为y元,
根据题意,得
解得
答:代驾服务在21:00-23:59的起步价是18元,超过5千米后每千米的收费为6元.
23.
解:(1)由题意,得
解得
(2)如图
24.设捐款10元的x人,捐款20元的y人,根据“45名同学共捐款900元”即可列方程组求解.
设捐款10元的x人,捐款20元的y人,由题意得
解得
答:捐款10元的12人,捐款20元的20人.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
