七年级数学下册试题 10.5用二元一次方程组解决问题--几何问题-苏科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 10.5用二元一次方程组解决问题--几何问题-苏科版(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 286.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 18:19:32 | ||
图片预览

文档简介
10.5用二元一次方程组解决问题--几何问题
一、选择题.
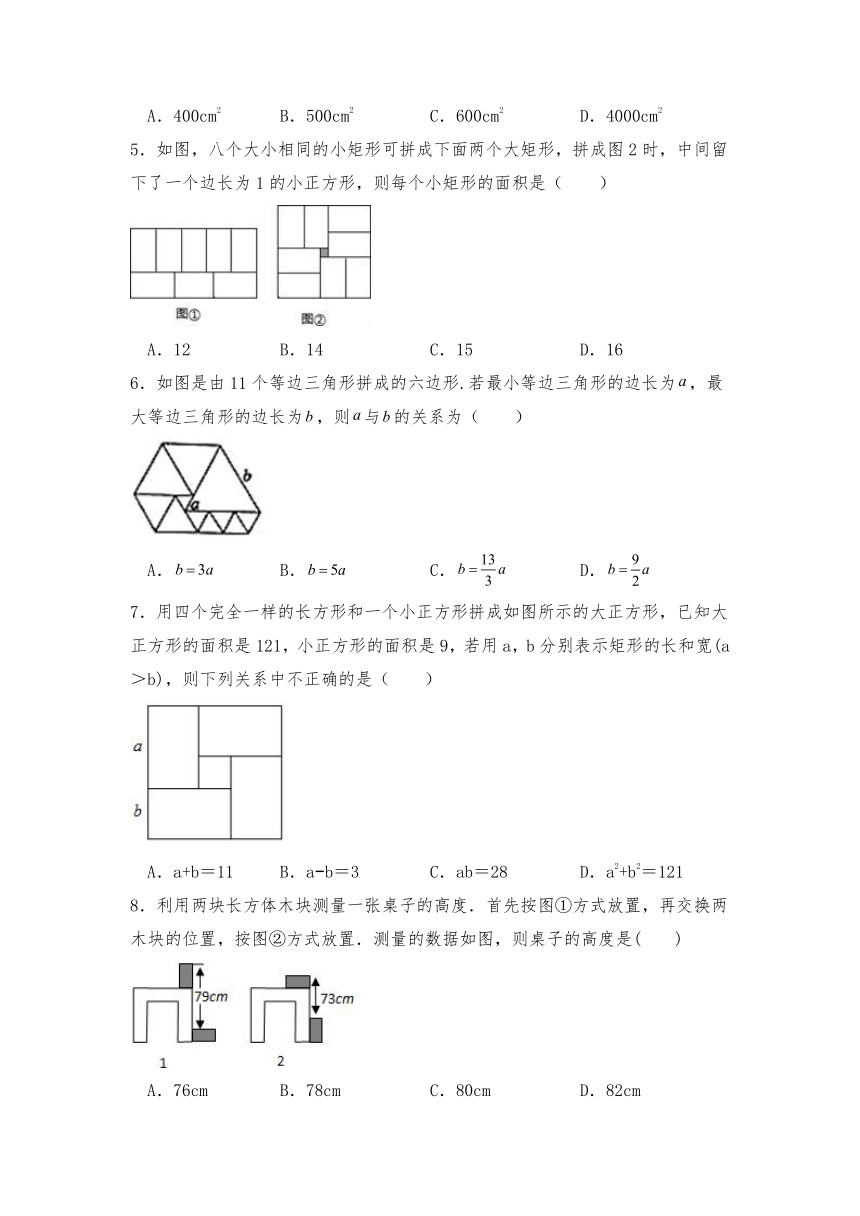
1.如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.10 B.15 C.45 D.25
2.用8块相同的长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,则每块地砖的长与宽分别是( )
A.25和20 B.30和20 C.40和35 D.45和15
3.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,设小长方形的长、宽分别为xcm,ycm,则下列方程组正确的是( )
A. B.
C. D.
4.如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
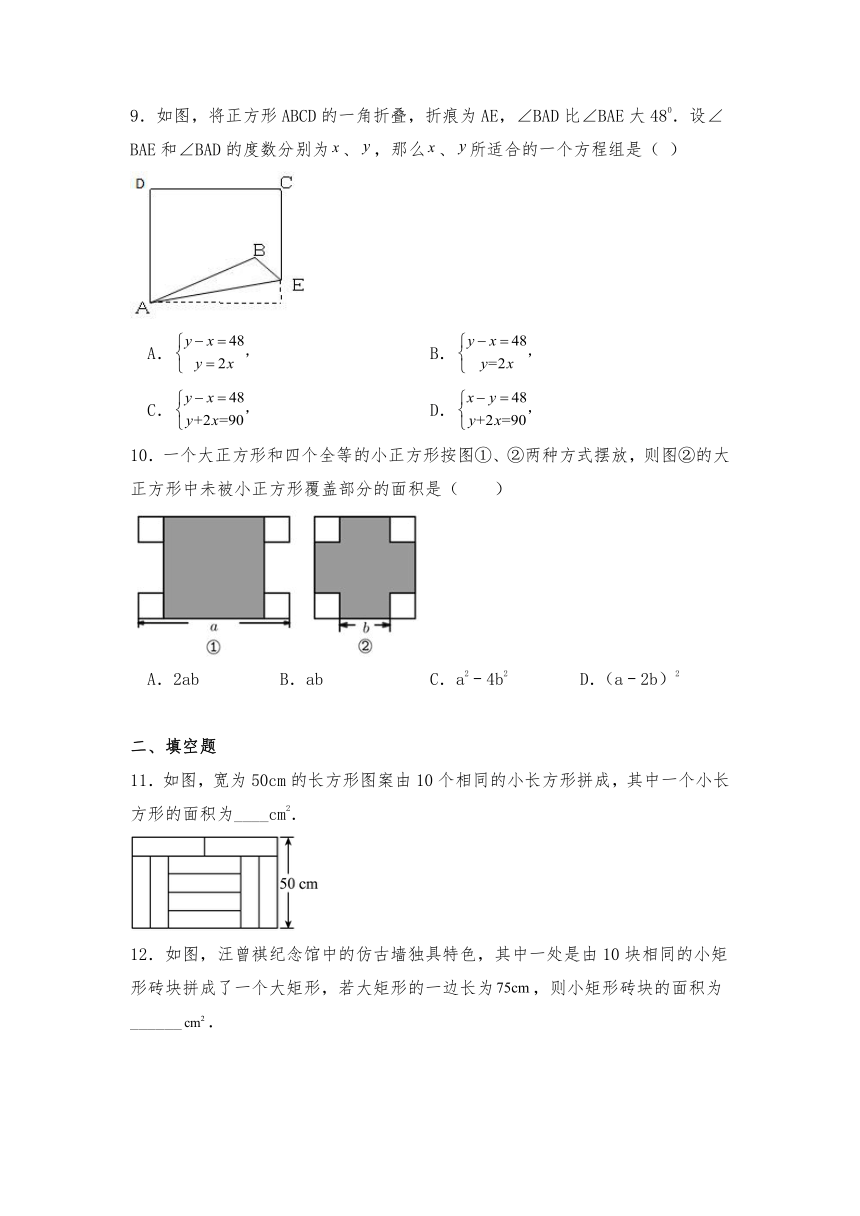
5.如图,八个大小相同的小矩形可拼成下面两个大矩形,拼成图2时,中间留下了一个边长为1的小正方形,则每个小矩形的面积是( )
A.12 B.14 C.15 D.16
6.如图是由11个等边三角形拼成的六边形.若最小等边三角形的边长为,最大等边三角形的边长为,则与的关系为( )
A. B. C. D.
7.用四个完全一样的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是121,小正方形的面积是9,若用a,b分别表示矩形的长和宽(a>b),则下列关系中不正确的是( )
A.a+b=11 B.a b=3 C.ab=28 D.a2+b2=121
8.利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
A.76cm B.78cm C.80cm D.82cm
9.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大480.设∠BAE和∠BAD的度数分别为、,那么、所适合的一个方程组是( )
A. B.
C. D.
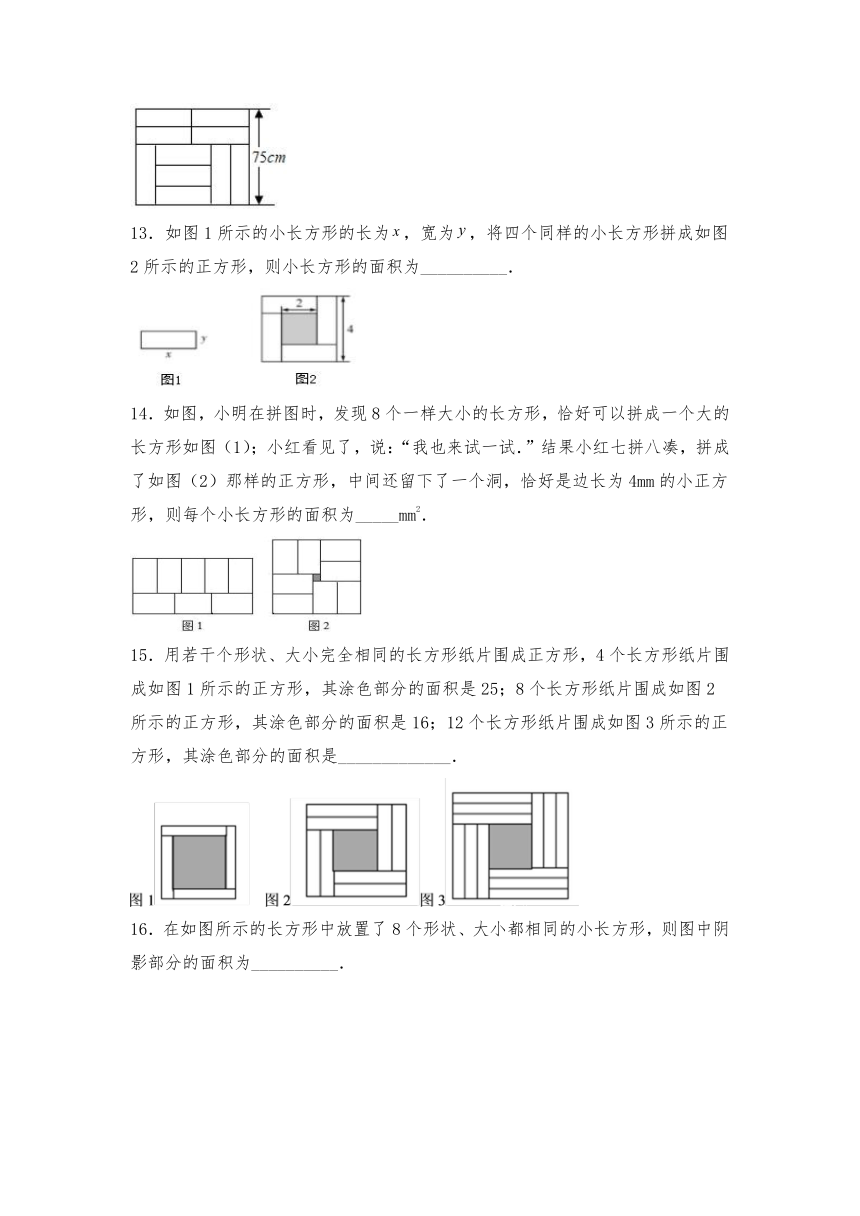
10.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.2ab B.ab C.a2﹣4b2 D.(a﹣2b)2
二、填空题
11.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为____cm2.
12.如图,汪曾祺纪念馆中的仿古墙独具特色,其中一处是由10块相同的小矩形砖块拼成了一个大矩形,若大矩形的一边长为,则小矩形砖块的面积为______.
13.如图1所示的小长方形的长为,宽为,将四个同样的小长方形拼成如图2所示的正方形,则小长方形的面积为__________.
14.如图,小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为4mm的小正方形,则每个小长方形的面积为_____mm2.
15.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是_____________.
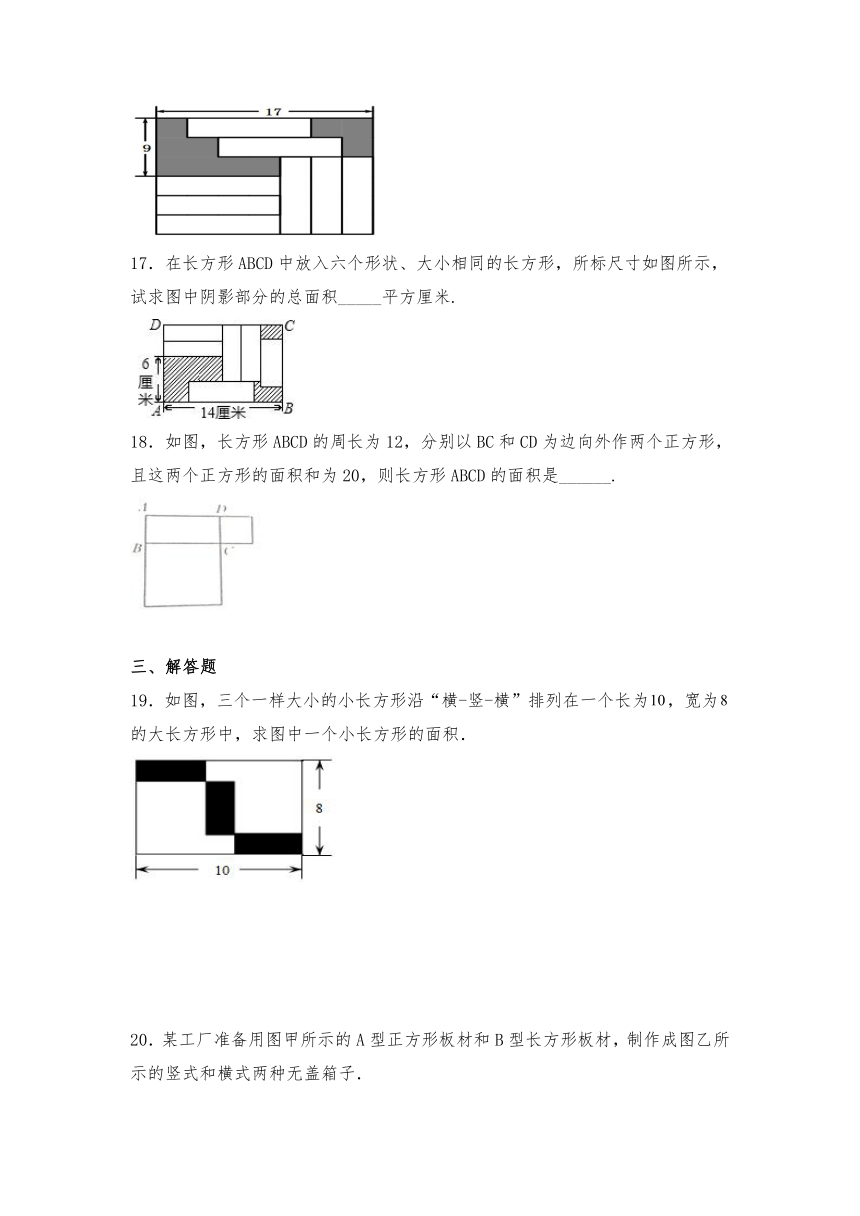
16.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为__________.
17.在长方形ABCD中放入六个形状、大小相同的长方形,所标尺寸如图所示,试求图中阴影部分的总面积_____平方厘米.
18.如图,长方形ABCD的周长为12,分别以BC和CD为边向外作两个正方形,且这两个正方形的面积和为20,则长方形ABCD的面积是______.
三、解答题
19.如图,三个一样大小的小长方形沿“横-竖-横”排列在一个长为,宽为的大长方形中,求图中一个小长方形的面积.
20.某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若现有A型板材150张,B型板材300张,可制作竖式和横式两种无盖箱子各多少个?
(2)若该工厂准备用不超过24000元资金去购买A、B两种型号板材,制作竖式、横式箱子共100个,已知A型板材每张20元,B型板材每张60元,问最多可以制作竖式箱子多少个?
(3)若该工厂新购得65张规格为的C型正方形板材,将其全部切割成A型或B型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10个,且材料恰好用完,则最多可以制作竖式箱子多少个?
21.某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图2),再将它们制作成甲乙两种无盖的长方体小盒(如图1).现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒,可以做成甲乙两种小盒各多少个?(注:图1中向上的一面无盖)
22.(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.
23.用若干块如左图所示的正方形或长方形纸片拼成图(1)和图(2)
(1)如图(1),若AD=7,AB=8,求与的值;
(2)如图(1),若长方形ABCD的面积为35,其中阴影部分的面积为20,求长方形ABCD的周长;
图(1)
(3)如图(2),若AD的长度为5,AB的长度为.
图(2)
①当=________,=_________时,,的值有无数组;
②当________,_________时,,的值不存在.
24.如图,正方形ABCD由四个相同的大长方形,四个相同的小长方形以及一个小正方形组成.其中四个大长方形的长和宽分别是小长方形长和宽的3倍,若中间小正方形的面积为1,求大正方形ABCD的面积.
答案
一、选择题
C.D.A.A.C.D.D.A.C.B
二、填空题
11.400
12.675
13.3
14.240
15.9
16.79
17.44
18.8.
三、解答题
19.
解:设小长方形的长为x,宽为y,
依题意得:,
解得:,
∴xy=4×2=8.
答:图中一个小长方形的面积为8.
20.
解:(1)设可制作竖式无盖箱子m个,可制作横式无盖箱子n个,依题意有
,
解得,
故可制作竖式无盖箱子30个,可制作横式无盖箱子60个;
(2)由题意可得,
1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,
设竖式箱子x个,则横式箱子(100-x)个,
(20+4×60)x+(2×20+3×60)(100-x)≤24000,
解得x≤50,
故x的最大值是50,
答:最多可以制作竖式箱子50个;
(3)C型可以看成三列,每一列可以做成3个A型或1个B型,65个C型就有65×3=195列,
∵材料恰好用完,
∴最后A型的数量一定是3的倍数,
设竖式a个,横式b个,
∵1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,1个B型相当于3个A型,
∴(1+4×3)a+(2+3×3)b=195×3,
∴13a+11b=585,
∵a、b均为整数,a≥10,
∴或或或,
故最多可以制作竖式箱子45个.
21.
解:设做成甲种小盒个,做成乙种小盒个
由题意知:
解得:
答:可以做成甲种小盒30个,乙种小盒60个.
22.
(1)设正方形A、B的边长分别为a、b,由题意得: ,
解得: ,
答:正方形A、B的边长分别为6,4;
(2)设正方形C、D的边长为c、d,则:
由图2得:(c-d)2=4,即:c2-2cd+d2=4,
由图3得:(c+d)2-c2-d2=48,即2dc=48,
∴c2+d2-48=4,
∴c2+d2=52,
即正方形C、D的面积和为52.
23.
解:(1)由图得
,
解得:,
(2)由图可得:5个小长方形面积=长方形ABCD的面积-阴影部分的面积,
∴,
∴ab=3,
∵阴影部分的面积为20,
∴,
∴,
∴a+b=,
方形ABCD的周长=2[(2a+b)+(2b+a)]=6(a+b)=6×4=24.
(3)由图(2)得:
,
由①得a=5-2b,③
将③代入②得2(5-2b)+mb=n,
∴(m-4)b=n-10,
∴当 时,a,b的解有无数组;
即m=4,n=10时,a,b的值有无数组;
当时,方程组无解,
即m=4,n≠10时,a,b的值不存在.
故答案为①m=4,n=10;②m=4,n≠10
24.
设小长方形的长为a,宽为b,则大长方形的长为3a,宽为3b,
由已知得: 解得:
∴正方形ABCD的边长AB=3a+3b=3×(2+1)=9,
∴正方形ABCD的面积为9×9=81.
一、选择题.
1.如图,在长为15,宽为12的矩形中,有形状、大小完全相同的5个小矩形,则图中阴影部分的面积为( )
A.10 B.15 C.45 D.25
2.用8块相同的长方形地砖拼成一块大长方形地面,地砖的拼放方式及相关数据如图所示,则每块地砖的长与宽分别是( )
A.25和20 B.30和20 C.40和35 D.45和15
3.在矩形ABCD中,放入六个形状、大小相同的长方形,所标尺寸如图所示,设小长方形的长、宽分别为xcm,ycm,则下列方程组正确的是( )
A. B.
C. D.
4.如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
5.如图,八个大小相同的小矩形可拼成下面两个大矩形,拼成图2时,中间留下了一个边长为1的小正方形,则每个小矩形的面积是( )
A.12 B.14 C.15 D.16
6.如图是由11个等边三角形拼成的六边形.若最小等边三角形的边长为,最大等边三角形的边长为,则与的关系为( )
A. B. C. D.
7.用四个完全一样的长方形和一个小正方形拼成如图所示的大正方形,已知大正方形的面积是121,小正方形的面积是9,若用a,b分别表示矩形的长和宽(a>b),则下列关系中不正确的是( )
A.a+b=11 B.a b=3 C.ab=28 D.a2+b2=121
8.利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
A.76cm B.78cm C.80cm D.82cm
9.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大480.设∠BAE和∠BAD的度数分别为、,那么、所适合的一个方程组是( )
A. B.
C. D.
10.一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中未被小正方形覆盖部分的面积是( )
A.2ab B.ab C.a2﹣4b2 D.(a﹣2b)2
二、填空题
11.如图,宽为50cm的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积为____cm2.
12.如图,汪曾祺纪念馆中的仿古墙独具特色,其中一处是由10块相同的小矩形砖块拼成了一个大矩形,若大矩形的一边长为,则小矩形砖块的面积为______.
13.如图1所示的小长方形的长为,宽为,将四个同样的小长方形拼成如图2所示的正方形,则小长方形的面积为__________.
14.如图,小明在拼图时,发现8个一样大小的长方形,恰好可以拼成一个大的长方形如图(1);小红看见了,说:“我也来试一试.”结果小红七拼八凑,拼成了如图(2)那样的正方形,中间还留下了一个洞,恰好是边长为4mm的小正方形,则每个小长方形的面积为_____mm2.
15.用若干个形状、大小完全相同的长方形纸片围成正方形,4个长方形纸片围成如图1所示的正方形,其涂色部分的面积是25;8个长方形纸片围成如图2所示的正方形,其涂色部分的面积是16;12个长方形纸片围成如图3所示的正方形,其涂色部分的面积是_____________.
16.在如图所示的长方形中放置了8个形状、大小都相同的小长方形,则图中阴影部分的面积为__________.
17.在长方形ABCD中放入六个形状、大小相同的长方形,所标尺寸如图所示,试求图中阴影部分的总面积_____平方厘米.
18.如图,长方形ABCD的周长为12,分别以BC和CD为边向外作两个正方形,且这两个正方形的面积和为20,则长方形ABCD的面积是______.
三、解答题
19.如图,三个一样大小的小长方形沿“横-竖-横”排列在一个长为,宽为的大长方形中,求图中一个小长方形的面积.
20.某工厂准备用图甲所示的A型正方形板材和B型长方形板材,制作成图乙所示的竖式和横式两种无盖箱子.
(1)若现有A型板材150张,B型板材300张,可制作竖式和横式两种无盖箱子各多少个?
(2)若该工厂准备用不超过24000元资金去购买A、B两种型号板材,制作竖式、横式箱子共100个,已知A型板材每张20元,B型板材每张60元,问最多可以制作竖式箱子多少个?
(3)若该工厂新购得65张规格为的C型正方形板材,将其全部切割成A型或B型板材(不计损耗),用切割的板材制作两种类型的箱子,要求竖式箱子不少于10个,且材料恰好用完,则最多可以制作竖式箱子多少个?
21.某纸品加工厂利用边角料裁出正方形和长方形两种硬纸片,长方形的宽与正方形的边长相等(如图2),再将它们制作成甲乙两种无盖的长方体小盒(如图1).现将300张长方形硬纸片和150张正方形硬纸片全部用于制作这两种小盒,可以做成甲乙两种小盒各多少个?(注:图1中向上的一面无盖)
22.(1)如图1,将两张正方形纸片A与三张正方形纸片B放在一起(不重叠无缝隙),拼成一个宽为10的长方形,求正方形纸片A、B的边长.
(2)如图2,将一张正方形纸片D放在一正方形纸片C的内部,阴影部分的面积为4;如图3,将正方形纸片C、D各一张并列放置后构造一个新的正方形,阴影部分的面积为48,求正方形C、D的面积之和.
23.用若干块如左图所示的正方形或长方形纸片拼成图(1)和图(2)
(1)如图(1),若AD=7,AB=8,求与的值;
(2)如图(1),若长方形ABCD的面积为35,其中阴影部分的面积为20,求长方形ABCD的周长;
图(1)
(3)如图(2),若AD的长度为5,AB的长度为.
图(2)
①当=________,=_________时,,的值有无数组;
②当________,_________时,,的值不存在.
24.如图,正方形ABCD由四个相同的大长方形,四个相同的小长方形以及一个小正方形组成.其中四个大长方形的长和宽分别是小长方形长和宽的3倍,若中间小正方形的面积为1,求大正方形ABCD的面积.
答案
一、选择题
C.D.A.A.C.D.D.A.C.B
二、填空题
11.400
12.675
13.3
14.240
15.9
16.79
17.44
18.8.
三、解答题
19.
解:设小长方形的长为x,宽为y,
依题意得:,
解得:,
∴xy=4×2=8.
答:图中一个小长方形的面积为8.
20.
解:(1)设可制作竖式无盖箱子m个,可制作横式无盖箱子n个,依题意有
,
解得,
故可制作竖式无盖箱子30个,可制作横式无盖箱子60个;
(2)由题意可得,
1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,
设竖式箱子x个,则横式箱子(100-x)个,
(20+4×60)x+(2×20+3×60)(100-x)≤24000,
解得x≤50,
故x的最大值是50,
答:最多可以制作竖式箱子50个;
(3)C型可以看成三列,每一列可以做成3个A型或1个B型,65个C型就有65×3=195列,
∵材料恰好用完,
∴最后A型的数量一定是3的倍数,
设竖式a个,横式b个,
∵1个竖式箱子需要1个A型和4个B型,1个横式箱子需要2个A型和3个B型,1个B型相当于3个A型,
∴(1+4×3)a+(2+3×3)b=195×3,
∴13a+11b=585,
∵a、b均为整数,a≥10,
∴或或或,
故最多可以制作竖式箱子45个.
21.
解:设做成甲种小盒个,做成乙种小盒个
由题意知:
解得:
答:可以做成甲种小盒30个,乙种小盒60个.
22.
(1)设正方形A、B的边长分别为a、b,由题意得: ,
解得: ,
答:正方形A、B的边长分别为6,4;
(2)设正方形C、D的边长为c、d,则:
由图2得:(c-d)2=4,即:c2-2cd+d2=4,
由图3得:(c+d)2-c2-d2=48,即2dc=48,
∴c2+d2-48=4,
∴c2+d2=52,
即正方形C、D的面积和为52.
23.
解:(1)由图得
,
解得:,
(2)由图可得:5个小长方形面积=长方形ABCD的面积-阴影部分的面积,
∴,
∴ab=3,
∵阴影部分的面积为20,
∴,
∴,
∴a+b=,
方形ABCD的周长=2[(2a+b)+(2b+a)]=6(a+b)=6×4=24.
(3)由图(2)得:
,
由①得a=5-2b,③
将③代入②得2(5-2b)+mb=n,
∴(m-4)b=n-10,
∴当 时,a,b的解有无数组;
即m=4,n=10时,a,b的值有无数组;
当时,方程组无解,
即m=4,n≠10时,a,b的值不存在.
故答案为①m=4,n=10;②m=4,n≠10
24.
设小长方形的长为a,宽为b,则大长方形的长为3a,宽为3b,
由已知得: 解得:
∴正方形ABCD的边长AB=3a+3b=3×(2+1)=9,
∴正方形ABCD的面积为9×9=81.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
