七年级数学下册试题 12.3互逆命题-苏科版(含答案)
文档属性
| 名称 | 七年级数学下册试题 12.3互逆命题-苏科版(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 103.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 00:00:00 | ||
图片预览




文档简介
12.3互逆命题
一、选择题.
1.下列正确叙述的个数是( )
①每个命题都有逆命题
②真命题的逆命题是真命题
③假命题的逆命题是真命题
④每个定理都有逆定理
⑤每个定理一定有逆命题
⑥命题“若a=b,那么a3=b3”的逆命题是假命题.
A.1 B.2 C.3 D.4
2.已知命题:如果a=b,那么|a|=|b|.该命题的逆命题是( )
A.如果a=b,那么|a|=|b| B.如果|a|=|b|,那么a=b
C.如果a≠b,那么|a|≠|b| D.如果|a|≠|b|,那么a≠b
3.下列命题:
①同旁内角互补,两直线平行;②若|a|=|b|,则a=b;③直角都相等;④相等的角是对顶角.
它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
4.给出下列4个命题:①同旁内角互补,两直线平行;②若|a|=|b|,则a=b;③直角都相等;④对顶角相等,它们的逆命题是真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
5.下列命题:①同旁内角互补,两直线平行;②若a2=b2,则a=b;③锐角与钝角互为补角;④相等的角是对顶角.它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
6.命题“如果a=b,那么|a|=|b|”的逆命题是假命题,可取下面哪组值反例说明( )
A.a=1,b=1 B.a=﹣1,b=﹣1 C.a=1,b=2 D.a=﹣1,b=1
7.下列命题中,真命题的个数有( )
①立方根等于它本身的数有两个,是0和1
②同位角相等
③平面内,过一点有且只有一条直线与已知直线平行
④对顶角相等
A.0个 B.1个 C.2个 D.3个
8.下列命题是假命题的是( )
A.同角的余角相等
B.两直线平行,同位角相等
C.n边形的外角和总是360°
D.同旁内角互补
9.下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
10.下列命题:①同旁内角互补,两直线平行;②直角都相等;③直角三角形没有钝角;④若a=b,则a2=b2.其中,它们的逆命题是真命题的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.命题“如a=b,那么|a|=|b|”的逆命题是 命题.(填“真”或“假”)
12.对于命题“如果a=b,那么ac=bc.”,它的逆命题是 命题.(填“真”或“假”)
13.命题:“两直线平行,则同旁内角互补”的逆命题为 .
14.命题“如果a2=b2,那么a=b”的逆命题是 命题(填“真”或“假”).
15.命题“若a=b,则﹣a=﹣b”的逆命题是 .
16.命题“若a=b,则a2=b2”的逆命题是 .
17.命题“若a=b,则|a|=|b|”的逆命题是 .
18.“若a=b,则a2=b2”的逆命题是 命题.(填“真”或“假”)
三、解答题
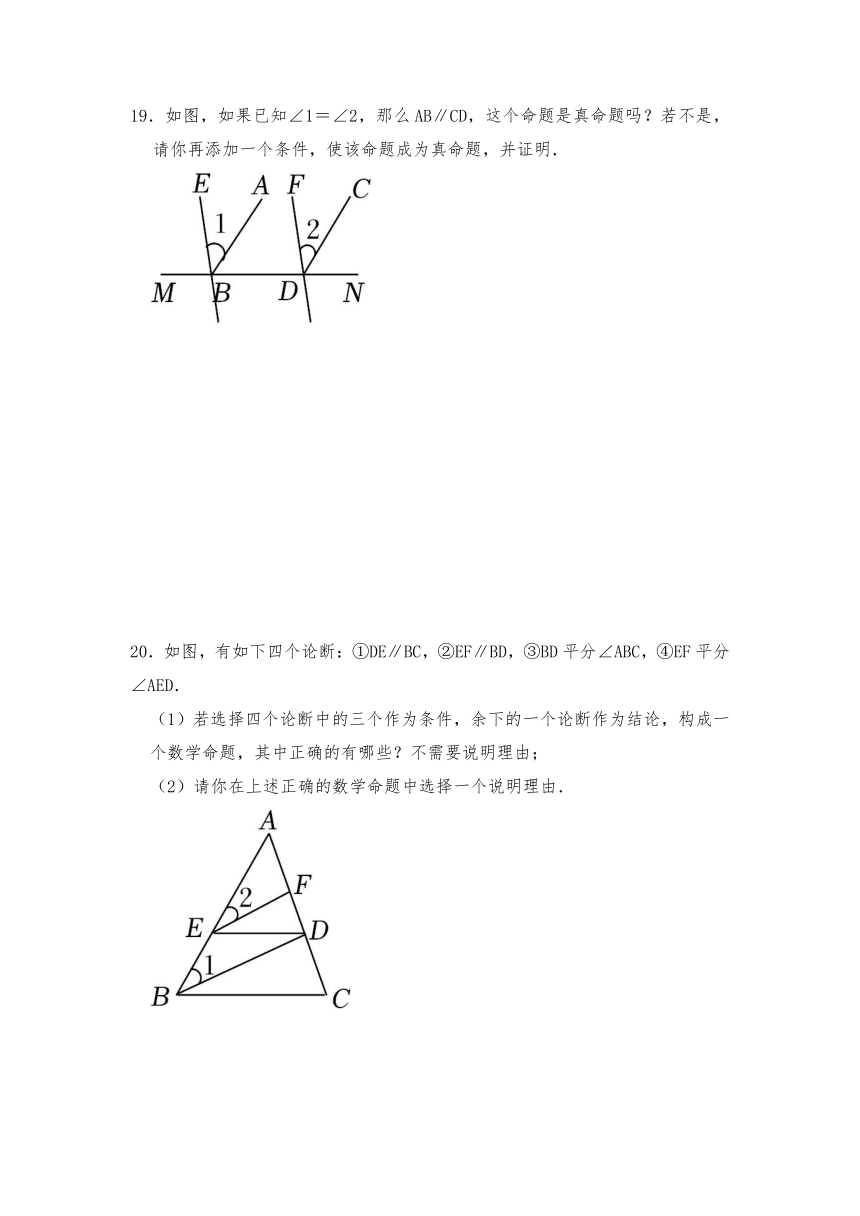
19.如图,如果已知∠1=∠2,那么AB∥CD,这个命题是真命题吗?若不是,请你再添加一个条件,使该命题成为真命题,并证明.
20.如图,有如下四个论断:①DE∥BC,②EF∥BD,③BD平分∠ABC,④EF平分∠AED.
(1)若选择四个论断中的三个作为条件,余下的一个论断作为结论,构成一个数学命题,其中正确的有哪些?不需要说明理由;
(2)请你在上述正确的数学命题中选择一个说明理由.
21.如图,∠ABC的两边分别与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)在图1中,射线BA与ED同向,BC与EF也同向,∠B与∠E的数量关系是: ;
(2)在图2中,射线BA与ED异向,BC与EF也异向,∠B与∠E的数量关系是: ;
(3)在图3中,射线BA与ED同向,BC与EF异向,∠B与∠E有怎样的数量关系,并说明理由;
(4)通过上面(1)、(2)、(3),你可得到的结论是:如果一个角的两边分别平行于另一个角的两边,则这两个角的关系是 .
(5)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的3倍少60°,请直接写出这两个角的度数.
22.如图,有以下四个条件:①AC∥DE,②DC∥EF,③CD平分∠BCA,④EF平分∠BED.
(1)若CD平分∠BCA,AC∥DE,DC∥EF,求证:EF平分∠BED.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
23.(1)如图,设DE∥BC,∠1=∠3,CD⊥AB,求证:FG⊥AB;
(2)若把(1)的题设中的DE∥BC”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“∠1=∠3”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由.
24.如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
答案
一、选择题.
B.B.B.B.B.D.B.D.B.A.
二、填空题
11.假.
12.假.
13.同旁内角互补,两直线平行.
14.真.
15.若﹣a=﹣b,则a=b
16.若a2=b2,则a=b.
17.|a|=|b|,则a=b
18.假.
三、解答题)
19.解:如果已知∠1=∠2,那么AB∥CD,不是真命题,
添加条件为:BE∥DF,
证明过程如下:
∵BE∥DF,
∴∠MBE=∠BDF,
∵∠1=∠2,
∴∠MBA=∠BDC,
∴AB∥CD.
20.(1)正确的命题有:
①②③为条件,④为结论;
①②④为条件,③为结论;
①③④为条件,②为结论;
②③④为条件,①为结论.
(2)若DE∥BC,EF∥BD,BD平分∠ABC,则EF平分∠AED.
证明如下:
∵DE∥BC,
∴∠AED=∠ABC,
∵EF∥BD,
∴∠AEF=∠ABD,
∵∠AED=∠AEF+∠FED,∠ABC=∠ABD+∠DBC,
∴∠FED=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠AEF=∠DBC∠DEF,
∴∠AEF=∠DEF,
∴EF平分∠AED.
21.
解:(1)∠B=∠E;
(2)∠B=∠E;
(3)∠B+∠E=180°;
理由是:BC与DE交于点O,如图,
∵BA∥ED,BC∥EF,
∴∠B=∠DOC,∠BOE+∠E=180°,
∵∠DOC=∠BOE,
∴∠B+∠E=180°;
(4)相等或互补;
(5)设另一个角是x,则这个角是2x﹣30°,
根据“若两个角的两边互相平行,则这两个角相等或互补”得:
x=3x﹣60°或x+3x﹣60°=180°,
解得x=30°或x=60°,
30°×3﹣60°=30°,
60°×3﹣60°=120°,
∵一个角比另一个角的3倍少60°,
∴这两个角不相等,
∴两个角的度数分别是60°、120°.
22.(1)证明:∵CD平分∠BCA,
∴∠BCD=∠ACD,
∵DC∥EF,
∴∠BCD=∠BEF,∠DEF=∠CDE,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠BEF=∠DEF,即EF平分∠BED.
(2)解:如果EF平分∠BED,AC∥DE,DC∥EF,那么CD平分∠BCA.
证明:∵EF平分∠BED,
∴∠BEF=∠DEF,
∵DC∥EF,
∴∠BCD=∠BEF,∠DEF=∠CDE,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠BCD=∠ACD,即CD平分∠BCA.
23.解:(1)∵DE∥BC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∴CD∥FG,
∵CD⊥AB,
∴FG⊥AB;
(2)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴DE∥BC;
(3)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵DE∥BC,
∴∠1=∠2,
∴∠1=∠3.
24.解:(1)可以构造3个命题,
命题1,如果AB∥CD,∠B=∠C,那么∠E=∠F;
命题2,如果AB∥CD,∠E=∠F,那么∠B=∠C;
命题3,如果∠E=∠F,∠B=∠C,那么AB∥CD;
(2)构造的3个命题都是真命题,
证明命题1,
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠CDF=∠C,
∴AC∥BD,
∴∠E=∠F.
一、选择题.
1.下列正确叙述的个数是( )
①每个命题都有逆命题
②真命题的逆命题是真命题
③假命题的逆命题是真命题
④每个定理都有逆定理
⑤每个定理一定有逆命题
⑥命题“若a=b,那么a3=b3”的逆命题是假命题.
A.1 B.2 C.3 D.4
2.已知命题:如果a=b,那么|a|=|b|.该命题的逆命题是( )
A.如果a=b,那么|a|=|b| B.如果|a|=|b|,那么a=b
C.如果a≠b,那么|a|≠|b| D.如果|a|≠|b|,那么a≠b
3.下列命题:
①同旁内角互补,两直线平行;②若|a|=|b|,则a=b;③直角都相等;④相等的角是对顶角.
它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
4.给出下列4个命题:①同旁内角互补,两直线平行;②若|a|=|b|,则a=b;③直角都相等;④对顶角相等,它们的逆命题是真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
5.下列命题:①同旁内角互补,两直线平行;②若a2=b2,则a=b;③锐角与钝角互为补角;④相等的角是对顶角.它们的逆命题是真命题的个数是( )
A.4个 B.3个 C.2个 D.1个
6.命题“如果a=b,那么|a|=|b|”的逆命题是假命题,可取下面哪组值反例说明( )
A.a=1,b=1 B.a=﹣1,b=﹣1 C.a=1,b=2 D.a=﹣1,b=1
7.下列命题中,真命题的个数有( )
①立方根等于它本身的数有两个,是0和1
②同位角相等
③平面内,过一点有且只有一条直线与已知直线平行
④对顶角相等
A.0个 B.1个 C.2个 D.3个
8.下列命题是假命题的是( )
A.同角的余角相等
B.两直线平行,同位角相等
C.n边形的外角和总是360°
D.同旁内角互补
9.下列命题中是真命题的是( )
A.相等的角是对顶角
B.如果a3=b3,那么a=b
C.三角形的一个外角等于两个内角之和
D.内错角相等
10.下列命题:①同旁内角互补,两直线平行;②直角都相等;③直角三角形没有钝角;④若a=b,则a2=b2.其中,它们的逆命题是真命题的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.命题“如a=b,那么|a|=|b|”的逆命题是 命题.(填“真”或“假”)
12.对于命题“如果a=b,那么ac=bc.”,它的逆命题是 命题.(填“真”或“假”)
13.命题:“两直线平行,则同旁内角互补”的逆命题为 .
14.命题“如果a2=b2,那么a=b”的逆命题是 命题(填“真”或“假”).
15.命题“若a=b,则﹣a=﹣b”的逆命题是 .
16.命题“若a=b,则a2=b2”的逆命题是 .
17.命题“若a=b,则|a|=|b|”的逆命题是 .
18.“若a=b,则a2=b2”的逆命题是 命题.(填“真”或“假”)
三、解答题
19.如图,如果已知∠1=∠2,那么AB∥CD,这个命题是真命题吗?若不是,请你再添加一个条件,使该命题成为真命题,并证明.
20.如图,有如下四个论断:①DE∥BC,②EF∥BD,③BD平分∠ABC,④EF平分∠AED.
(1)若选择四个论断中的三个作为条件,余下的一个论断作为结论,构成一个数学命题,其中正确的有哪些?不需要说明理由;
(2)请你在上述正确的数学命题中选择一个说明理由.
21.如图,∠ABC的两边分别与∠DEF的两边平行,即BA∥ED,BC∥EF.
(1)在图1中,射线BA与ED同向,BC与EF也同向,∠B与∠E的数量关系是: ;
(2)在图2中,射线BA与ED异向,BC与EF也异向,∠B与∠E的数量关系是: ;
(3)在图3中,射线BA与ED同向,BC与EF异向,∠B与∠E有怎样的数量关系,并说明理由;
(4)通过上面(1)、(2)、(3),你可得到的结论是:如果一个角的两边分别平行于另一个角的两边,则这两个角的关系是 .
(5)应用②中的真命题,解决以下问题:
若两个角的两边互相平行,且一个角比另一个角的3倍少60°,请直接写出这两个角的度数.
22.如图,有以下四个条件:①AC∥DE,②DC∥EF,③CD平分∠BCA,④EF平分∠BED.
(1)若CD平分∠BCA,AC∥DE,DC∥EF,求证:EF平分∠BED.
(2)除(1)外,请再选择四个条件中的三个作为题设,余下的一个作为结论,写出一个真命题,再给予证明.
23.(1)如图,设DE∥BC,∠1=∠3,CD⊥AB,求证:FG⊥AB;
(2)若把(1)的题设中的DE∥BC”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由;
(3)若把(1)的题设中的“∠1=∠3”与结论中的“FG⊥AB”对调后,命题还成立吗?说明理由.
24.如图,现有以下三个条件:①AB∥CD,②∠B=∠C,③∠E=∠F.请你以其中两个作为题设,另一个作为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?若是真命题,请给予证明;若是假命题,请举出反例(证明其中的一个命题即可).
答案
一、选择题.
B.B.B.B.B.D.B.D.B.A.
二、填空题
11.假.
12.假.
13.同旁内角互补,两直线平行.
14.真.
15.若﹣a=﹣b,则a=b
16.若a2=b2,则a=b.
17.|a|=|b|,则a=b
18.假.
三、解答题)
19.解:如果已知∠1=∠2,那么AB∥CD,不是真命题,
添加条件为:BE∥DF,
证明过程如下:
∵BE∥DF,
∴∠MBE=∠BDF,
∵∠1=∠2,
∴∠MBA=∠BDC,
∴AB∥CD.
20.(1)正确的命题有:
①②③为条件,④为结论;
①②④为条件,③为结论;
①③④为条件,②为结论;
②③④为条件,①为结论.
(2)若DE∥BC,EF∥BD,BD平分∠ABC,则EF平分∠AED.
证明如下:
∵DE∥BC,
∴∠AED=∠ABC,
∵EF∥BD,
∴∠AEF=∠ABD,
∵∠AED=∠AEF+∠FED,∠ABC=∠ABD+∠DBC,
∴∠FED=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠AEF=∠DBC∠DEF,
∴∠AEF=∠DEF,
∴EF平分∠AED.
21.
解:(1)∠B=∠E;
(2)∠B=∠E;
(3)∠B+∠E=180°;
理由是:BC与DE交于点O,如图,
∵BA∥ED,BC∥EF,
∴∠B=∠DOC,∠BOE+∠E=180°,
∵∠DOC=∠BOE,
∴∠B+∠E=180°;
(4)相等或互补;
(5)设另一个角是x,则这个角是2x﹣30°,
根据“若两个角的两边互相平行,则这两个角相等或互补”得:
x=3x﹣60°或x+3x﹣60°=180°,
解得x=30°或x=60°,
30°×3﹣60°=30°,
60°×3﹣60°=120°,
∵一个角比另一个角的3倍少60°,
∴这两个角不相等,
∴两个角的度数分别是60°、120°.
22.(1)证明:∵CD平分∠BCA,
∴∠BCD=∠ACD,
∵DC∥EF,
∴∠BCD=∠BEF,∠DEF=∠CDE,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠BEF=∠DEF,即EF平分∠BED.
(2)解:如果EF平分∠BED,AC∥DE,DC∥EF,那么CD平分∠BCA.
证明:∵EF平分∠BED,
∴∠BEF=∠DEF,
∵DC∥EF,
∴∠BCD=∠BEF,∠DEF=∠CDE,
∵AC∥DE,
∴∠ACD=∠CDE,
∴∠BCD=∠ACD,即CD平分∠BCA.
23.解:(1)∵DE∥BC,
∴∠1=∠2,
∵∠1=∠3,
∴∠2=∠3,
∴CD∥FG,
∵CD⊥AB,
∴FG⊥AB;
(2)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵∠1=∠3,
∴∠1=∠2,
∴DE∥BC;
(3)成立,
理由是:∵FG⊥AB,CD⊥AB,
∴CD∥FG,
∴∠2=∠3,
∵DE∥BC,
∴∠1=∠2,
∴∠1=∠3.
24.解:(1)可以构造3个命题,
命题1,如果AB∥CD,∠B=∠C,那么∠E=∠F;
命题2,如果AB∥CD,∠E=∠F,那么∠B=∠C;
命题3,如果∠E=∠F,∠B=∠C,那么AB∥CD;
(2)构造的3个命题都是真命题,
证明命题1,
∵AB∥CD,
∴∠B=∠CDF,
∵∠B=∠C,
∴∠CDF=∠C,
∴AC∥BD,
∴∠E=∠F.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
