能追上小明吗课件

课件27张PPT。第七节 能追上小明吗龟兔赛跑 已知兔子的速度为每秒9米，乌龟的速度为每
秒0.05米，兔子跑了10分钟 ，然后睡了一觉，
乌龟追上兔子需要多长时间？ 解：兔子十分钟跑了
9× 600=5400（米）乌龟跑5400米需要
5400÷ 0.05=108000（秒）108000秒 = 30小时
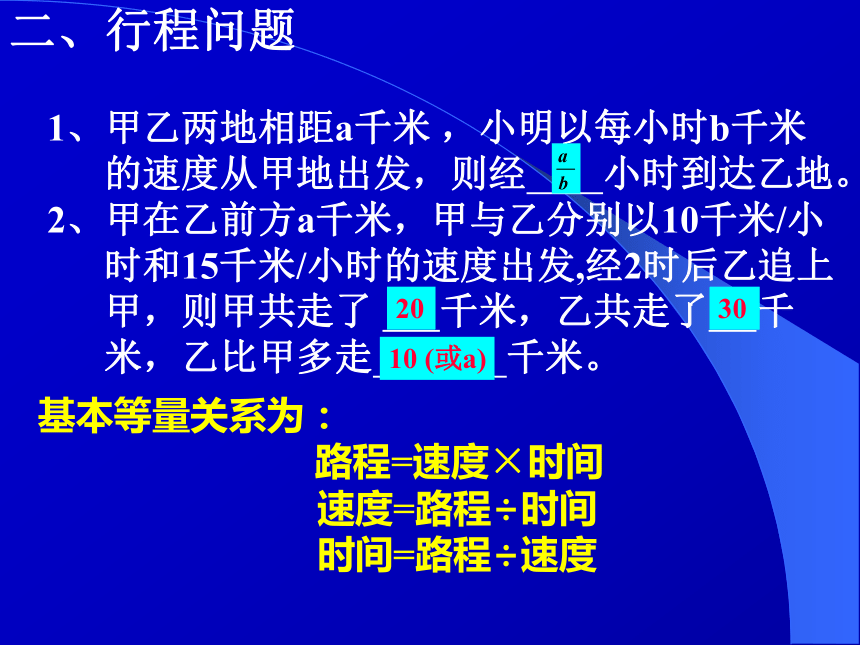
因此乌龟追不上兔子。二、行程问题

1、甲乙两地相距a千米 ，小明以每小时b千米
的速度从甲地出发，则经 小时到达乙地。
2、甲在乙前方a千米，甲与乙分别以10千米/小
时和15千米/小时的速度出发,经2时后乙追上
甲，则甲共走了 千米，乙共走了 千
米，乙比甲多走 千米。 203010 (或a)基本等量关系为：
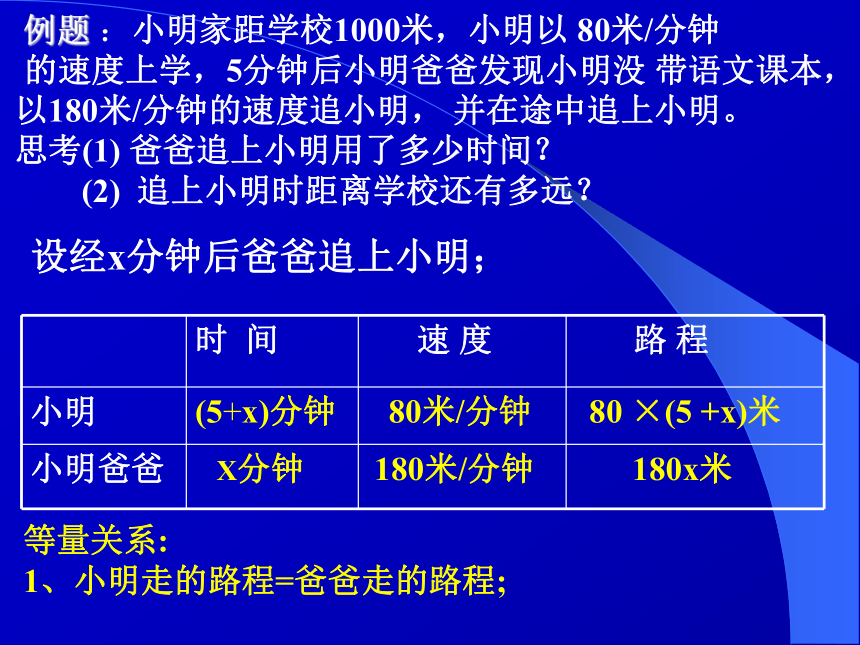
路程=速度×时间速度=路程÷时间 时间=路程÷速度 例1 ：小明家距学校1000米，小明以 80米/分钟
的速度上学，5分钟后小明爸爸发现小明没 带语文课本，以180米/分钟的速度追小明， 并在途中追上小明。
思考(1) 爸爸追上小明用了多少时间？
(2) 追上小明时距离学校还有多远？ 分析：等量关系:
1、小明走的路程=爸爸走的路程;2、小明走的总时间—爸爸追的时间=5分钟家学校爸爸小明设经x分钟后爸爸追上小明；80 ×(5 +x)米180x米80米/分钟180米/分钟(5+x)分钟X分钟等量关系:
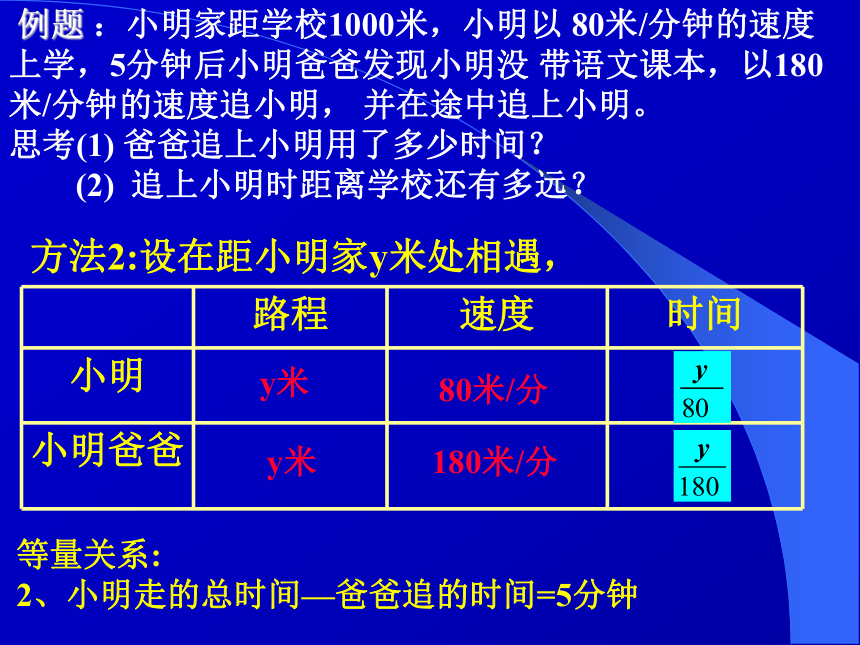
1、小明走的路程=爸爸走的路程; 例题 ：小明家距学校1000米，小明以 80米/分钟
的速度上学，5分钟后小明爸爸发现小明没 带语文课本，以180米/分钟的速度追小明， 并在途中追上小明。
思考(1) 爸爸追上小明用了多少时间？
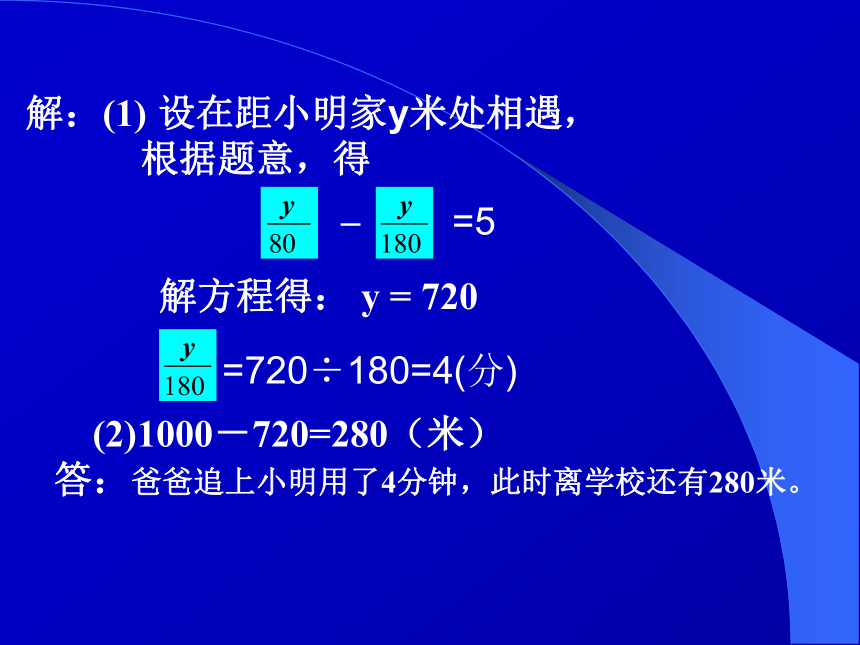
(2) 追上小明时距离学校还有多远？ 解：(1)设经 x 分钟后爸爸追上小明，
　　　根据题意，得
180x = 80×5 + 80x
解方程得： x = 4
(2)1000－180×4=280（米）
答：爸爸追上小明用了4分钟，此时离学校还有280米。 方法2:设在距小明家y米处相遇，y米y米80米/分180米/分等量关系:
2、小明走的总时间—爸爸追的时间=5分钟 例题 ：小明家距学校1000米，小明以 80米/分钟的速度上学，5分钟后小明爸爸发现小明没 带语文课本，以180米/分钟的速度追小明， 并在途中追上小明。
思考(1) 爸爸追上小明用了多少时间？
(2) 追上小明时距离学校还有多远？ 问题1：后队追上前队用了多长时间 ？议一议:育红学校七年级学生步行到郊外旅行，1班的学生组成前队，步行的速度为4千米/小时，2班的学生组成后队，速度为6千米/小时，前队出发１小时后，后队出发， 同时后队派一名联络员骑自行车在两队之间不间断地 来回进行联络，他骑车的速度为12千米 /小时。请根据以上的事实提出问题并尝试回答。问题2：后队追上前队时联络员行了多少路程？问题3：联络员第一次追上前队时用了多长时间？问题4：当后队追上前队时，他们已经行进了多少路程？问题5：联络员在前队出发多少时间后第一次追上前队？
………………问题1：后队追上前队用了多长时间 ？ 育红学校七年级学生步行到郊外旅行，1班的学生组成
前队，步行的速度为4千米/小时，2班的学生组成后队，
速度为6千米/小时，前队出发１小时后，后队出发，
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络，他骑车的速度为12千米 /小时。 解：设后队追上前队用了x小时，
根据题意，得： 6x = 4x + 4×1解方程得：x =2答：后队追上前队时用了2小时。问题2：后队追上前队时联络员行了多少路程？ 育红学校七年级学生步行到郊外旅行，1班的学生组成
前队，步行的速度为4千米/小时，2班的学生组成后队，
速度为6千米/小时，前队出发１小时后，后队出发，
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络，他骑车的速度为12千米 /小时。解：由问题1得后队追上前队用了2小时，因此
联络员共行进了 12 × 2 = 24 （千米）
答：后队追上前队时联络员行了24千米。问题3：联络员第一次追上前队时用了多长时间？ 育红学校七年级学生步行到郊外旅行，1班的学生组成
前队，步行的速度为4千米/小时，2班的学生组成后队，
速度为6千米/小时，前队出发１小时后，后队出发，
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络，他骑车的速度为12千米 /小时。 解：设联络员第一次追上前队时用了x小时，
根据题意，得： 12x = 4x + 4×1解方程得：x =0.5答：联络员第一次追上前队时用了0.5小时。问题4：当后队追上前队时，他们已经行进了多少路程？ 育红学校七年级学生步行到郊外旅行，1班的学生组成
前队，步行的速度为4千米/小时，2班的学生组成后队，
速度为6千米/小时，前队出发１小时后，后队出发，
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络，他骑车的速度为12千米 /小时。解：设当后队追上前队时，他们已经行进了x千米，
根据题意，得： 解方程得： x = 12
答：当后队追上前队时，他们已经行进12千米.问题5：联络员在前队出发多少时间后第一次追上前队？ 育红学校七年级学生步行到郊外旅行，1班的学生组成
前队，步行的速度为4千米/小时，2班的学生组成后队，
速度为6千米/小时，前队出发１小时后，后队出发，
同时后队派一名联络员骑自行车在两队之间不间断地
来回进行联络，他骑车的速度为12千米 /小时。 解：设联络员在前队出发x小时后第一次追上前队，
根据题意，得： 答：联络员在前队出发后1.5 小时后第一次追上前队.4x = 12（x - 1） 解方程得： x = 1.5小结（1）从时间考虑：
速度慢的用时－速度快的用时＝多用的时间（2）从路程考虑：
速度快的行程－速度慢的行程＝两者的距离行程问题中的基本等量关系为：
路程=速度×时间，
一般可从下面两个方面寻找追及问题中的等量关系： 解决路程问题的关键是什么？找出等量关系的重要方法是：找出等量关系，列出方程。画线段图。作业：p192. 习题5.10
问题解决 1、2题布置作业例2：甲乙两人相距40千米，甲在后乙在前，两人同向而行，甲先出发1.5小时后乙再出发，甲的速度为每小时8千米，乙的速度为每小时6千米，甲出发几小时后追上乙？解：设甲出发x小时后追上乙，根据题意，得：8x – 6（x – 1.5）= 40答：甲出发后15.5小时追上乙。甲乙40千米解方程得：x = 15.5 例3 一条船在两个码头之间航行，顺水时需要4.5
小时，逆水返回需要5小时，水流速度是1千
米/时。这两个码头相距多少千米？ 分析：逆水速度＝船在静水中的速度－水速顺水速度＝船在静水中的速度＋水速等量关系：1、顺水的行程=逆水的行程2、船在静水中速度不变解：设船在静水中速度为x千米/小时。解：设两码头相距y千米。例4 甲、乙两人在400米的环形跑道上散步，甲每分钟走110米，乙每分钟走90米，两人同时从一个地点出发，几分钟后两人第一次相遇？分析：在环形跑道上运动，分两种情况：已知：V甲〉V乙图一所示实为 问题图二所示实为 问题相遇追击例4 甲、乙两人在400米的环形跑道上散步，甲每分钟走110米，乙每分钟走90米，两人同时从一个地点出发，几分钟后两人第一次相遇。分析：在环形跑道上运动，分两种情况：甲的行程＋乙的行程=跑道一圈的周长 （2）同向而行：甲的行程－乙的行程=跑道一圈的周长 想一想 若把上题中的“第一次”相遇改为“第二次”
相遇需要时间又是多少呢？若改为“第n次”相遇呢？（1）背向而行：例5 在3点钟和4点钟之间，钟表上的
时针和分针什么时间重合？例6：甲步行上午7时从A地出发，于下午5时到达B地，乙骑自行车上午10时从A地出发，于下午3时到达B地，问乙在什么时间追上甲的？分析:
设A，B两地间的距离为1，根据题意得:
甲步行走全程需要10小时，则甲的速度为_______.
乙骑车走全程需要5小时，则乙的速度为_______.等量关系: 1、甲的用时=乙的用时+3小时

2、甲走的路程=乙走的路程.例6：甲步行上午7时从A地出发，于下午5时到达B地，乙骑自行车上午10时从A地出发，于下午3时到达B地，问乙在什么时间追上甲的？例6：甲步行上午7时从A地出发，于下午5时到达B地，乙骑自行车上午10时从A地出发，于下午3时到达B地，问乙在什么时间追上甲的？