1.3勾股定理的应用 课件 北师大版数学八年级上册(共39张PPT)
文档属性
| 名称 | 1.3勾股定理的应用 课件 北师大版数学八年级上册(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 440.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 18:36:56 | ||
图片预览











文档简介
(共39张PPT)
第一章 勾股定理
第4课 勾股定理的应用
数学(BS)版八年级上册
几何体表面上两点之间的最短距离
例1 如图,有一个圆柱形油罐,油罐的底面半径是2 m,高AB是5 m,要以点A环绕油罐建梯子,梯子的顶端正好到达点A的正上方的点B处,问梯子最短需多少米?(π取3)
新课学习
解:圆柱形油罐的侧面展开图如图,则AB′的长为梯子的最短长度.
因为AA′=2π×2=12,A′B′=AB=5,
在Rt△AA′B′中,由勾股定理,得AB′2=AA′^2 +(A′B′^2 ) =122+52=169=132.所以AB′=13.
答:梯子最短需13 m.
解:将长方体的侧面展开,如图,连接PQ,
则PQ的长即为所求的最短路程.
由题知PA=2×(4+2)=12,QA=5.
在Rt△PAQ中,由勾股定理,得PQ2=PA2+QA2=122+52=132.
所以PQ=13.
答:蚂蚁爬行的最短路程为13 cm.
1.如图,长方体的底面边长分别为 2 cm 和4 cm,高为 5 cm.若一只蚂蚁从点P开始经过4个侧面爬行一周到达点Q,求蚂蚁爬行的最短路程.
解决几何体表面上两点之间最短路线问题的关键步骤:(1)把立体图形展开成平面图形;(2)确定最短路线;(3)确定直角三角形;(4)根据直角三角形的边长,利用勾股定理求解.
利用方程思想解决实际问题
例2 【教材P15习题T6变式】如图所示,小强想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m 后(即BC=5 m),发现下端刚好接触地面,你能帮他算出旗杆的高度吗?若能,请计算出AC的长;若不能,请说明理由.
解:能.设AC=x,则AB=x+1.
在Rt△ACB中,∠ACB=90°,BC=5,
由勾股定理,得AB2=AC2+BC2,
即(x+1)2=x2+52.解得x=12.
答:AC的长为12 m.
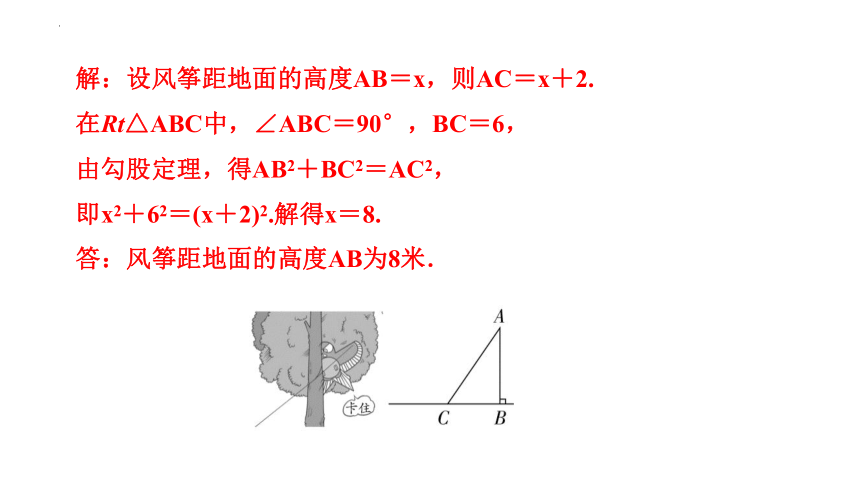
2.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度,于是他先拉住风筝线垂直到地面上,发现风筝线多出2米,然后把风筝线沿直线BC向后拉开6米(即BC=6米),发现风筝线末端刚好接触地面,求风筝距地面的高度AB.
解:设风筝距地面的高度AB=x,则AC=x+2.
在Rt△ABC中,∠ABC=90°,BC=6,
由勾股定理,得AB2+BC2=AC2,
即x2+62=(x+2)2.解得x=8.
答:风筝距地面的高度AB为8米.
勾股定理逆定理的应用
例3 如图,如果只给你一把带有刻度的直尺,你能否检验∠P是不是直角?简述你的方法,并说明理由.
解:能检验.
方法:①在射线PM上截取PA,使得PA为3 cm,确定点A的位置,在射线PN上截取PB,使得PB为4 cm,确定点B的位置;
②连接AB,得△PAB;
③用刻度尺测量AB的长度,若AB恰为5 cm,则说明∠P是直角,否则,∠P不是直角.
理由如下:
在△PAB中,PA=3,PB=4,PA2+PB2=32+42=52,
若AB=5,则PA2+PB2=AB2.
所以△PAB是直角三角形,∠P是直角.(答案不唯一)
3.如图所示,某会场准备在其周围的一块四边形空地上种植草坪进行绿化,经测量∠B=90°,AB=7 m,BC=24 m,CD=15 m,AD=20 m,求这块四边形草坪ABCD的面积.
解:如图所示,连接AC.
在Rt△ABC中,由勾股定理,得AC2=AB2+BC2=72+242=625.
在△ADC中,AD2+CD2=202+152=625=AC2,
所以△ADC为直角三角形,∠ADC=90°.
所以S四边形ABCD=S△ABC+S△ADC=AB·BC+AD·CD=×7×24+×20×15=84+150=234(m2).
答:这块四边形草坪ABCD的面积是234 m2.
1.如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的点C测得CA=130 m,CB=120 m,则AB的长为( C )
A.30 m
B.40 m
C.50 m
D.60 m
C
基础巩固
2.李老师要做一个直角三角形教具,做好后量得三边长分别是30 cm,40 cm和50 cm,则这个教具 合格 .(填“合格”或“不合格”)
合格
3.(2022·金华)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( C )
C
4.如图所示,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿哪个方向航行吗?
解:根据题意可知,BM=8×2=16(海里),
BP=15×2=30(海里).
在△BMP中,BM2+BP2=162+302=256+900=1 156.
又PM2=342=1 156,所以BM2+BP2=PM2.
所以△BMP是直角三角形,∠MBP=90°.
所以180°-90°-60°=30°.
答:乙船沿南偏东30°方向航行.
5.方程思想 如图,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为直线).如果两只猴子所经过的路程相等,求这棵树的高.
解:设BD=x.由题意知BC+AC=BD+AD,
所以AD=30-x.
在Rt△ACD中,由勾股定理,得(10+x)2+202=(30-x)2.
解得x=5.所以x+10=15.
答:这棵树的高为15 m.
6.一根长18 cm的牙刷置于底面直径为5 cm、高为12 cm的圆柱形水杯中,牙刷露在杯子外面的长度为h cm,则h的取值范围是( C )
A.5B.6C.5≤h≤6
D.6≤h≤7
C
7.如图,将一个边长分别为4,8的长方形纸片沿EF折叠,使点C与点A重合,则BE的长为 3 .
3
8.分类讨论如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体木块的对角顶点G处,若AB=3 cm,BC=5 cm,BF=6 cm,则蜘蛛要在长方体表面上沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
解:可能有三种方案,如下:
方案一:如图1,当蜘蛛从点A出发经过EF再到点G时,连接AG.
因为BC=5,
所以FG=BC=5.
所以BG=FG+BF=5+6=11.
在Rt△ABG中,AG2=AB2+BG2=32+112=130.
方案二:如图2,当蜘蛛从点A出发经过BF再到点G时,连接AG.
因为AB=3,BC=5,
所以AC=AB+BC=3+5=8.
因为BF=6,所以CG=BF=6.
在Rt△ACG中,AG2=AC2+CG2=82+62=100.
方案三:如图3,当蜘蛛从点A出发经过HE再到点G时,连接AG.
因为AB=3,所以GH=AB=3.
因为BC=5,所以AD=BC=5.
因为BF=6,所以HD=BF=6.
所以DG=HD+GH=6+3=9.
在Rt△ADG中,AG2=DG2+AD2=92+52=106.
因为100<106<130,所以蜘蛛沿着第二种方案的路线爬行,才能最快抓到苍蝇,这时蜘蛛走过的路程是10 cm.
本课复习
1.机场入口处的铭牌上说明,飞机行李架是一个50 cm×40 cm×20 cm的长方体空间,有位旅客想购买一件画卷随身携带,现有4种长度的画卷:①38 cm;②40 cm;③60 cm;④68 cm.请问这位旅客可以购买的尺寸是( B )
A.①②
B.①②③
C.①②③④
D.①
B
2.如图,一个底面圆周长为24 m,高为5 m的圆柱体,一只蚂蚁沿其侧表面从点A到点B所经过的最短路线长为( C )
A.12 m
B.15 m
C.13 m
D.9.13 m
C
3.如图,墙A处需要维修,A处距离墙脚C处12米,墙下是一条宽BC为5米的小河,现要使用一架梯子维修A处的墙体,其中有一架12.8米长的梯子,则这架梯子 不能 (填“能”或“不能”)到达墙的A处.
不能
4.如图,有一只摆钟,摆锤看作一个点,当它摆动到离底座最近时,摆锤离底座的垂直高度DE=4 cm,当它来回摆动到离底座的距离最高与最低时的水平距离为8 cm时,摆锤离底座的垂直高度BF=6 cm,则钟摆AD的长度为 17 cm.
17
循环复习
5.在Rt△ABC中,∠C=90°, AC=1, AB2=10,则BC= 3 .
3
1.【教材P14随堂练习变式】如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( D )
A.25海里
B.30海里
C.35海里
D.40海里
D
基础提能
2.如图,有一个圆柱,其高为8 cm,它的底面周长为16 cm,在圆柱外侧距下底1 cm的A处有一只蚂蚁,它想吃到圆柱外侧距上底1 cm的B处的食物,则蚂蚁经过的最短路程为 10 cm.
第2题图
10
3.如图是一个三级台阶,它的每一级的长、宽和高分别为5 dm,3 dm和1 dm,A和B是这个台阶两个相对的端点,点A处有一只蚂蚁,想到点B处吃可口的食物.请你想一想,这只蚂蚁从点A出发,则沿着台阶面爬到点B的最短路程为 13 dm.
第3题图
13
4.如图是一个滑梯示意图,若将滑梯AC水平放置,则刚好与AB一样长,已知滑梯的高度CE=3 m,CD=1 m,求滑道AC的长.
解:设AC=x,则AB=AC=x.
由题意知EB=CD=1,所以AE=x-1.
在Rt△AEC中,∠AEC=90°,
由勾股定理,得AC2=CE2+AE2,
即x2=32+(x-1)2.
解得x=5.
所以滑道AC的长为5 m.
5.公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明.
解:公路AB段需要暂时封锁.
理由如下:
如图,过点C作CD⊥AB于点D.
在Rt△ABC中,∠ACB=90°,BC=400,AC=300,
由勾股定理,得AB2=AC2+BC2=3002+4002=5002.
所以AB=500.
因为S△ABC=AB·CD=BC·AC,
所以CD===240(米).
因为240<250,
所以公路AB段需要暂时封锁.
6.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400 m,BD=200 m,且CD=800 m,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少?
解:由题意,得AC=400,CD=800,BD=200.
如图,作点A关于直线CD对称的点A′,连接A′B交CD于点M,点M即为所求,即在M处饮水能使所走的总路程最短.过点A′作A′H⊥BD,交BD的延长线于点H,则BH=400+200=600(m).
由轴对称的性质可知A′M=AM.
所以AM+BM=A′M+BM=A′B.
在Rt△A′BH中,由勾股定理,得A′B2=A′H2+BH2=CD2+BH2=8002+6002=1 000 000.
所以A′B=1 000.所以最短路程是1 000 m.
第一章 勾股定理
第4课 勾股定理的应用
数学(BS)版八年级上册
几何体表面上两点之间的最短距离
例1 如图,有一个圆柱形油罐,油罐的底面半径是2 m,高AB是5 m,要以点A环绕油罐建梯子,梯子的顶端正好到达点A的正上方的点B处,问梯子最短需多少米?(π取3)
新课学习
解:圆柱形油罐的侧面展开图如图,则AB′的长为梯子的最短长度.
因为AA′=2π×2=12,A′B′=AB=5,
在Rt△AA′B′中,由勾股定理,得AB′2=AA′^2 +(A′B′^2 ) =122+52=169=132.所以AB′=13.
答:梯子最短需13 m.
解:将长方体的侧面展开,如图,连接PQ,
则PQ的长即为所求的最短路程.
由题知PA=2×(4+2)=12,QA=5.
在Rt△PAQ中,由勾股定理,得PQ2=PA2+QA2=122+52=132.
所以PQ=13.
答:蚂蚁爬行的最短路程为13 cm.
1.如图,长方体的底面边长分别为 2 cm 和4 cm,高为 5 cm.若一只蚂蚁从点P开始经过4个侧面爬行一周到达点Q,求蚂蚁爬行的最短路程.
解决几何体表面上两点之间最短路线问题的关键步骤:(1)把立体图形展开成平面图形;(2)确定最短路线;(3)确定直角三角形;(4)根据直角三角形的边长,利用勾股定理求解.
利用方程思想解决实际问题
例2 【教材P15习题T6变式】如图所示,小强想知道学校旗杆的高度,他发现旗杆顶端的绳子垂到地面还多1 m,当他把绳子的下端拉开5 m 后(即BC=5 m),发现下端刚好接触地面,你能帮他算出旗杆的高度吗?若能,请计算出AC的长;若不能,请说明理由.
解:能.设AC=x,则AB=x+1.
在Rt△ACB中,∠ACB=90°,BC=5,
由勾股定理,得AB2=AC2+BC2,
即(x+1)2=x2+52.解得x=12.
答:AC的长为12 m.
2.如图,小旭放风筝时,风筝线断了,风筝挂在了树上.他想知道风筝距地面的高度,于是他先拉住风筝线垂直到地面上,发现风筝线多出2米,然后把风筝线沿直线BC向后拉开6米(即BC=6米),发现风筝线末端刚好接触地面,求风筝距地面的高度AB.
解:设风筝距地面的高度AB=x,则AC=x+2.
在Rt△ABC中,∠ABC=90°,BC=6,
由勾股定理,得AB2+BC2=AC2,
即x2+62=(x+2)2.解得x=8.
答:风筝距地面的高度AB为8米.
勾股定理逆定理的应用
例3 如图,如果只给你一把带有刻度的直尺,你能否检验∠P是不是直角?简述你的方法,并说明理由.
解:能检验.
方法:①在射线PM上截取PA,使得PA为3 cm,确定点A的位置,在射线PN上截取PB,使得PB为4 cm,确定点B的位置;
②连接AB,得△PAB;
③用刻度尺测量AB的长度,若AB恰为5 cm,则说明∠P是直角,否则,∠P不是直角.
理由如下:
在△PAB中,PA=3,PB=4,PA2+PB2=32+42=52,
若AB=5,则PA2+PB2=AB2.
所以△PAB是直角三角形,∠P是直角.(答案不唯一)
3.如图所示,某会场准备在其周围的一块四边形空地上种植草坪进行绿化,经测量∠B=90°,AB=7 m,BC=24 m,CD=15 m,AD=20 m,求这块四边形草坪ABCD的面积.
解:如图所示,连接AC.
在Rt△ABC中,由勾股定理,得AC2=AB2+BC2=72+242=625.
在△ADC中,AD2+CD2=202+152=625=AC2,
所以△ADC为直角三角形,∠ADC=90°.
所以S四边形ABCD=S△ABC+S△ADC=AB·BC+AD·CD=×7×24+×20×15=84+150=234(m2).
答:这块四边形草坪ABCD的面积是234 m2.
1.如图,湖的两端有A,B两点,从与BA方向成直角的BC方向上的点C测得CA=130 m,CB=120 m,则AB的长为( C )
A.30 m
B.40 m
C.50 m
D.60 m
C
基础巩固
2.李老师要做一个直角三角形教具,做好后量得三边长分别是30 cm,40 cm和50 cm,则这个教具 合格 .(填“合格”或“不合格”)
合格
3.(2022·金华)如图,圆柱的底面直径为AB,高为AC,一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( C )
C
4.如图所示,在B港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里速度前进,乙船沿南偏东某方向以每小时15海里速度前进,2小时后甲船到M岛,乙船到P岛,两岛相距34海里,你知道乙船沿哪个方向航行吗?
解:根据题意可知,BM=8×2=16(海里),
BP=15×2=30(海里).
在△BMP中,BM2+BP2=162+302=256+900=1 156.
又PM2=342=1 156,所以BM2+BP2=PM2.
所以△BMP是直角三角形,∠MBP=90°.
所以180°-90°-60°=30°.
答:乙船沿南偏东30°方向航行.
5.方程思想 如图,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m处的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处(假设它跃过的路线为直线).如果两只猴子所经过的路程相等,求这棵树的高.
解:设BD=x.由题意知BC+AC=BD+AD,
所以AD=30-x.
在Rt△ACD中,由勾股定理,得(10+x)2+202=(30-x)2.
解得x=5.所以x+10=15.
答:这棵树的高为15 m.
6.一根长18 cm的牙刷置于底面直径为5 cm、高为12 cm的圆柱形水杯中,牙刷露在杯子外面的长度为h cm,则h的取值范围是( C )
A.5
D.6≤h≤7
C
7.如图,将一个边长分别为4,8的长方形纸片沿EF折叠,使点C与点A重合,则BE的长为 3 .
3
8.分类讨论如图,一只蜘蛛在一块长方体木块的一个顶点A处,一只苍蝇在这个长方体木块的对角顶点G处,若AB=3 cm,BC=5 cm,BF=6 cm,则蜘蛛要在长方体表面上沿着怎样的路线爬行,才能最快抓到苍蝇?这时蜘蛛走过的路程是多少厘米?
解:可能有三种方案,如下:
方案一:如图1,当蜘蛛从点A出发经过EF再到点G时,连接AG.
因为BC=5,
所以FG=BC=5.
所以BG=FG+BF=5+6=11.
在Rt△ABG中,AG2=AB2+BG2=32+112=130.
方案二:如图2,当蜘蛛从点A出发经过BF再到点G时,连接AG.
因为AB=3,BC=5,
所以AC=AB+BC=3+5=8.
因为BF=6,所以CG=BF=6.
在Rt△ACG中,AG2=AC2+CG2=82+62=100.
方案三:如图3,当蜘蛛从点A出发经过HE再到点G时,连接AG.
因为AB=3,所以GH=AB=3.
因为BC=5,所以AD=BC=5.
因为BF=6,所以HD=BF=6.
所以DG=HD+GH=6+3=9.
在Rt△ADG中,AG2=DG2+AD2=92+52=106.
因为100<106<130,所以蜘蛛沿着第二种方案的路线爬行,才能最快抓到苍蝇,这时蜘蛛走过的路程是10 cm.
本课复习
1.机场入口处的铭牌上说明,飞机行李架是一个50 cm×40 cm×20 cm的长方体空间,有位旅客想购买一件画卷随身携带,现有4种长度的画卷:①38 cm;②40 cm;③60 cm;④68 cm.请问这位旅客可以购买的尺寸是( B )
A.①②
B.①②③
C.①②③④
D.①
B
2.如图,一个底面圆周长为24 m,高为5 m的圆柱体,一只蚂蚁沿其侧表面从点A到点B所经过的最短路线长为( C )
A.12 m
B.15 m
C.13 m
D.9.13 m
C
3.如图,墙A处需要维修,A处距离墙脚C处12米,墙下是一条宽BC为5米的小河,现要使用一架梯子维修A处的墙体,其中有一架12.8米长的梯子,则这架梯子 不能 (填“能”或“不能”)到达墙的A处.
不能
4.如图,有一只摆钟,摆锤看作一个点,当它摆动到离底座最近时,摆锤离底座的垂直高度DE=4 cm,当它来回摆动到离底座的距离最高与最低时的水平距离为8 cm时,摆锤离底座的垂直高度BF=6 cm,则钟摆AD的长度为 17 cm.
17
循环复习
5.在Rt△ABC中,∠C=90°, AC=1, AB2=10,则BC= 3 .
3
1.【教材P14随堂练习变式】如图,一轮船以16海里/小时的速度从港口A出发向东北方向航行,另一轮船以12海里/小时的速度同时从港口A出发向东南方向航行,离开港口2小时后,两船相距( D )
A.25海里
B.30海里
C.35海里
D.40海里
D
基础提能
2.如图,有一个圆柱,其高为8 cm,它的底面周长为16 cm,在圆柱外侧距下底1 cm的A处有一只蚂蚁,它想吃到圆柱外侧距上底1 cm的B处的食物,则蚂蚁经过的最短路程为 10 cm.
第2题图
10
3.如图是一个三级台阶,它的每一级的长、宽和高分别为5 dm,3 dm和1 dm,A和B是这个台阶两个相对的端点,点A处有一只蚂蚁,想到点B处吃可口的食物.请你想一想,这只蚂蚁从点A出发,则沿着台阶面爬到点B的最短路程为 13 dm.
第3题图
13
4.如图是一个滑梯示意图,若将滑梯AC水平放置,则刚好与AB一样长,已知滑梯的高度CE=3 m,CD=1 m,求滑道AC的长.
解:设AC=x,则AB=AC=x.
由题意知EB=CD=1,所以AE=x-1.
在Rt△AEC中,∠AEC=90°,
由勾股定理,得AC2=CE2+AE2,
即x2=32+(x-1)2.
解得x=5.
所以滑道AC的长为5 m.
5.公路旁有一块山地正在开发,现有C处需要爆破.已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示.为了安全起见,爆破点C周围250米内不得进入,在进行爆破时,公路AB段是否需要暂时封锁?请通过计算进行说明.
解:公路AB段需要暂时封锁.
理由如下:
如图,过点C作CD⊥AB于点D.
在Rt△ABC中,∠ACB=90°,BC=400,AC=300,
由勾股定理,得AB2=AC2+BC2=3002+4002=5002.
所以AB=500.
因为S△ABC=AB·CD=BC·AC,
所以CD===240(米).
因为240<250,
所以公路AB段需要暂时封锁.
6.如图,牧童在A处放牛,其家在B处,A,B到河岸的距离分别为AC=400 m,BD=200 m,且CD=800 m,牧童从A处把牛牵到河边饮水后回家,问在何处饮水能使所走的总路程最短?最短路程是多少?
解:由题意,得AC=400,CD=800,BD=200.
如图,作点A关于直线CD对称的点A′,连接A′B交CD于点M,点M即为所求,即在M处饮水能使所走的总路程最短.过点A′作A′H⊥BD,交BD的延长线于点H,则BH=400+200=600(m).
由轴对称的性质可知A′M=AM.
所以AM+BM=A′M+BM=A′B.
在Rt△A′BH中,由勾股定理,得A′B2=A′H2+BH2=CD2+BH2=8002+6002=1 000 000.
所以A′B=1 000.所以最短路程是1 000 m.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
