6.2 实数 课件(3课时、共55张PPT) 沪科版数学七年级下册
文档属性
| 名称 | 6.2 实数 课件(3课时、共55张PPT) 沪科版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 725.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 00:00:00 | ||
图片预览









文档简介
(共55张PPT)
6.2 实数
第1课时 无理数与实数的概念
沪科版·七年级下册
新课导入
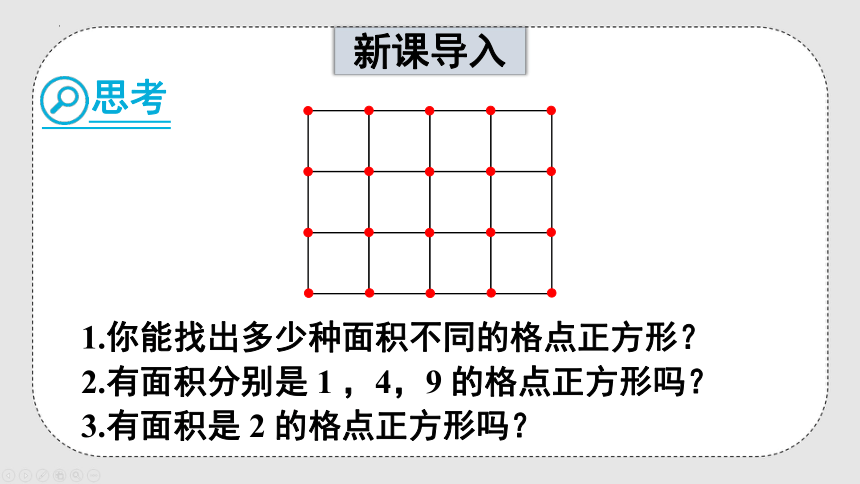
思考
1.你能找出多少种面积不同的格点正方形?
2.有面积分别是 1 ,4,9 的格点正方形吗?
3.有面积是 2 的格点正方形吗?
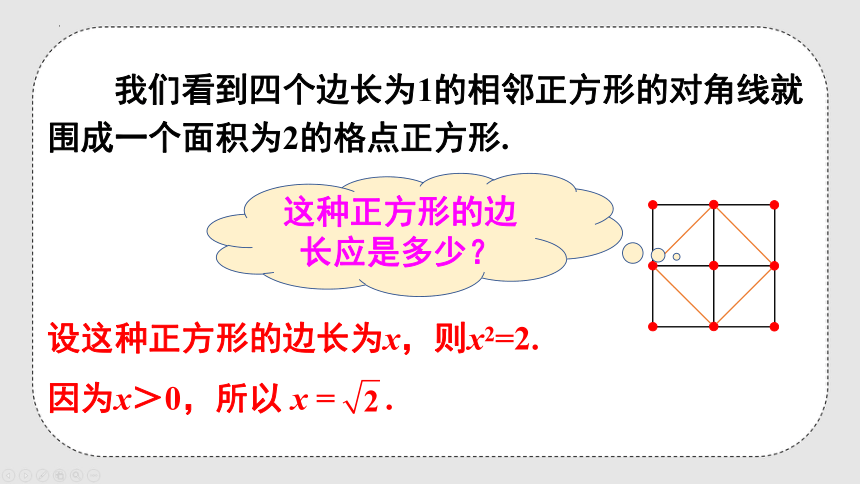
我们看到四个边长为1的相邻正方形的对角线就围成一个面积为2的格点正方形.
这种正方形的边长应是多少?
设这种正方形的边长为x,则x2=2.
因为x>0,所以 x = .
进行新课
问: 是不是整数?是不是分数?是不是有理数?
有多大
a
a
类似地,可得
……
像上面这样一直(无限)做下去,我们可以得到:
这说明 是一个无限不循环小数.
我们把这种无限不循环小数叫做无理数.
思考:你知道哪些数是无理数
1.圆周率π及一些含有π的数都是无理数.
例如:
2.开不尽方的数都是无理数.
像 都是无理数.
注意:带根号的数不一定是无理数.
例如:
因为 ,所以 是有理数.
3.有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
168.3232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分由相继的正整数组成〕
无理数也像有理数一样广泛存在着.
无理数也有正负之分,例如:
正无理数:
负无理数:
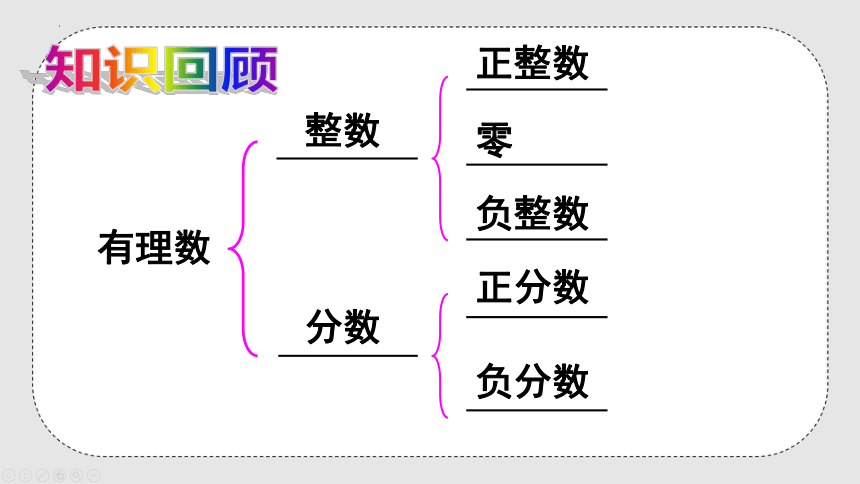
知识回顾
有理数
整数
分数
正整数
零
负整数
正分数
负分数
知识回顾
思考:有理数还有分类方法吗?
有理数
正有理数
零
负有理数
知识回顾
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数(均可化为分数)
无理数(不可化为分数)
概念整理
有理数和无理数统称实数.
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
在 中,
练 习
属于有理数的:________________________________
属于无理数的:________________________________
属于实数的有:________________________________
随堂练习
1. 有理数和无理数的区别在于( )
A.有理数都是有限小数,无理数都是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正的,无理数是负的
D.有理数是正数,无理数是分数
B
2. 把下列各数填入相应的括号内:
(1)有理数:{ };
(2)无理数:{ };
(3)正实数:{ };
(4)实数:{ }.
3. 试将下列各数进行分类(用两种不同的标准分类):
4. 写出满足条件:①是负数;②是无限不循环小数的一个数是________.
5. 在 0,1,2,3,4,5,6,7,8,9,10 这11个数中,
(1)______的平方根和______的立方根是有理数;
(2)____________的平方根和______________的立方根是无理数.
﹣π
答案不唯一
0,1,4,9
0,1,8
2,3,5,6,7,8,10
2,3,4,5,6,7,9,10
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P12练习1-3;
2.完成练习册本课时的习题。
第2课时 实数的性质
沪科版·七年级下册
新课导入
思考
每一个有理数都可用数轴上的一个点来表示,无理数(如 )能用数轴上的点表示吗?
试一试
你能在数轴上找到表示 的点吗?
进行新课
如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
C
-2
-1
0
1
2
C
B
A
3
试一试
你能在数轴上找到表示 的点吗?
-2
-1
0
1
2
4
5
6
思考
如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
归纳小结
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样.例如:
与 互为相反数,有 .
与 互为倒数,有 .
任何一个实数 a 的绝对值仍然用|a|表示,如:
填一填
1. a 是一个实数,它的相反数为________,绝对值为________.
2. 如果 a ≠ 0,那么它的倒数为________.
3. 正实数的绝对值是________,0 的绝对值是_____,负实数的绝对值是___________.
4.在数轴上距离表示-2的点是 个单位长度的数是_
________________.
﹣a
|a|
它本身
0
它的相反数
随堂练习
1. 与数轴上的点一一对应的是( )
A. 有理数 B. 分数或整数
C. 无理数 D. 实数
D
2. 求下列各数的相反数和绝对值.
(1) ;(2) ;(3) .
解:(1) 的相反数为 ,绝对值为 .
(2) 的相反数为 ,绝对值为
(3)π-3的相反数为3-π,因为π>3,所以绝对值为|π-3|=π-3.
3. 已知 a 为实数,则下列四个数中一定为非负数的是( )
A. a B.
C.|﹣a| D.﹣|﹣a|
C
4. 若实数 a,b 互为相反数 c,d 互为倒数,求
的值.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第3题;
2.完成练习册本课时的习题。
第3课时 实数的运算及大小比较
沪科版·七年级下册
复习导入
1.用字母来表示有理数的乘法交换律、乘法结合律、乘法分配律.
乘法交换律:ab=ba
乘法结合律:(ab)c =a(bc)
乘法分配律:(a+b)c =ac+bc
2.用字母表示有理数的加法交换律和结合律.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
3.平方差公式、完全平方公式.
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式: (a±b)2=a2±2ab+b2
4.有理数的混合运算顺序.
先算乘方,再算乘除,最后算加减,有括号的要先算括号里面的.
当数从有理数扩充到实数以后,实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对于实数仍然适用.
进行新课
讨论 下列各式错在哪里
练一练:计算下列各式的值:
解:
解:
实数范围内的运算法则及运算顺序与有理数范围内是一样的.
归纳小结
例1 近似计算:
(1) (精确到0.01);
(2) (精确到0.1).
解:
在实数运算中,当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算.
归纳小结
例2 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
2
-3
-2
-1
0
1
3
4
5
解:
由数轴上各点的位置,得
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点所表示的数.在实数范围内也有:
正数大于零,负数小于零,正数大于负数.
两个正数,绝对值大的数较大.
两个负数,绝对值大的数反而小.
试一试
比较下列各组里两个数的大小:
随堂练习
1. 下列说法不正确的是( )
A.互为相反数的两个实数的和是有理数
B.互为倒数的两个实数的积是有理数
C.绝对值相等的两个实数的差是有理数
D.两个无理数的和可能是有理数
C
2. 计算:
(1) (精确到个位);
(2) (精确到 0.01).
11
2.58
3. 将下列各数表示在数轴上,并回答问题:
(1)将上面几个数用“<”连接起来;
(2)数轴上表示 和﹣2这两个数的点之间的距离是______.
4. 下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.
5. 介于 和 之间的整数是( )
A.2 B.3 C.4 D.5
6. 估计与0.5的大小关系是: ___ 0.5 .(填“>”“=”或“<”)
D
B
>
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第4,5题;
2.完成练习册本课时的习题。
6.2 实数
第1课时 无理数与实数的概念
沪科版·七年级下册
新课导入
思考
1.你能找出多少种面积不同的格点正方形?
2.有面积分别是 1 ,4,9 的格点正方形吗?
3.有面积是 2 的格点正方形吗?
我们看到四个边长为1的相邻正方形的对角线就围成一个面积为2的格点正方形.
这种正方形的边长应是多少?
设这种正方形的边长为x,则x2=2.
因为x>0,所以 x = .
进行新课
问: 是不是整数?是不是分数?是不是有理数?
有多大
a
a
类似地,可得
……
像上面这样一直(无限)做下去,我们可以得到:
这说明 是一个无限不循环小数.
我们把这种无限不循环小数叫做无理数.
思考:你知道哪些数是无理数
1.圆周率π及一些含有π的数都是无理数.
例如:
2.开不尽方的数都是无理数.
像 都是无理数.
注意:带根号的数不一定是无理数.
例如:
因为 ,所以 是有理数.
3.有一定的规律,但不循环的无限小数都是无理数.
例如:
0.1010010001…〔两个1之间依次多1个0〕
168.3232232223…〔两个3之间依次多1个2〕
0.12345678910111213 …〔小数部分由相继的正整数组成〕
无理数也像有理数一样广泛存在着.
无理数也有正负之分,例如:
正无理数:
负无理数:
知识回顾
有理数
整数
分数
正整数
零
负整数
正分数
负分数
知识回顾
思考:有理数还有分类方法吗?
有理数
正有理数
零
负有理数
知识回顾
小数
有限小数
无限小数
无限循环小数
无限不循环小数
有理数(均可化为分数)
无理数(不可化为分数)
概念整理
有理数和无理数统称实数.
实数
有理数
无理数
正有理数
零
负有理数
正无理数
负无理数
有限小数或无限循环小数
无限不循环小数
在 中,
练 习
属于有理数的:________________________________
属于无理数的:________________________________
属于实数的有:________________________________
随堂练习
1. 有理数和无理数的区别在于( )
A.有理数都是有限小数,无理数都是无限小数
B.有理数能用分数表示,而无理数不能
C.有理数是正的,无理数是负的
D.有理数是正数,无理数是分数
B
2. 把下列各数填入相应的括号内:
(1)有理数:{ };
(2)无理数:{ };
(3)正实数:{ };
(4)实数:{ }.
3. 试将下列各数进行分类(用两种不同的标准分类):
4. 写出满足条件:①是负数;②是无限不循环小数的一个数是________.
5. 在 0,1,2,3,4,5,6,7,8,9,10 这11个数中,
(1)______的平方根和______的立方根是有理数;
(2)____________的平方根和______________的立方根是无理数.
﹣π
答案不唯一
0,1,4,9
0,1,8
2,3,5,6,7,8,10
2,3,4,5,6,7,9,10
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P12练习1-3;
2.完成练习册本课时的习题。
第2课时 实数的性质
沪科版·七年级下册
新课导入
思考
每一个有理数都可用数轴上的一个点来表示,无理数(如 )能用数轴上的点表示吗?
试一试
你能在数轴上找到表示 的点吗?
进行新课
如下图,以单位长度为边长画一个正方形,以原点为圆心,正方形对角线为半径画弧,与正、负半轴的交点分别为点A和点B,数轴上A点和B点对应的数是什么?
-2
-1
0
1
2
C
-2
-1
0
1
2
C
B
A
3
试一试
你能在数轴上找到表示 的点吗?
-2
-1
0
1
2
4
5
6
思考
如果将所有的有理数都标到数轴上,那么数轴将被填满吗?
如果再将所有的无理数都标到数轴上,那么数轴被填满了吗?
归纳小结
总结:数轴上的任一点必定表示一个实数;反过来,每一个实数(有理数或无理数)也都可以用数轴上的一个点来表示.
即:实数与数轴上的点一一对应.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样.例如:
与 互为相反数,有 .
与 互为倒数,有 .
任何一个实数 a 的绝对值仍然用|a|表示,如:
填一填
1. a 是一个实数,它的相反数为________,绝对值为________.
2. 如果 a ≠ 0,那么它的倒数为________.
3. 正实数的绝对值是________,0 的绝对值是_____,负实数的绝对值是___________.
4.在数轴上距离表示-2的点是 个单位长度的数是_
________________.
﹣a
|a|
它本身
0
它的相反数
随堂练习
1. 与数轴上的点一一对应的是( )
A. 有理数 B. 分数或整数
C. 无理数 D. 实数
D
2. 求下列各数的相反数和绝对值.
(1) ;(2) ;(3) .
解:(1) 的相反数为 ,绝对值为 .
(2) 的相反数为 ,绝对值为
(3)π-3的相反数为3-π,因为π>3,所以绝对值为|π-3|=π-3.
3. 已知 a 为实数,则下列四个数中一定为非负数的是( )
A. a B.
C.|﹣a| D.﹣|﹣a|
C
4. 若实数 a,b 互为相反数 c,d 互为倒数,求
的值.
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第3题;
2.完成练习册本课时的习题。
第3课时 实数的运算及大小比较
沪科版·七年级下册
复习导入
1.用字母来表示有理数的乘法交换律、乘法结合律、乘法分配律.
乘法交换律:ab=ba
乘法结合律:(ab)c =a(bc)
乘法分配律:(a+b)c =ac+bc
2.用字母表示有理数的加法交换律和结合律.
加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
3.平方差公式、完全平方公式.
平方差公式:a2-b2=(a+b)(a-b)
完全平方公式: (a±b)2=a2±2ab+b2
4.有理数的混合运算顺序.
先算乘方,再算乘除,最后算加减,有括号的要先算括号里面的.
当数从有理数扩充到实数以后,实数和有理数一样,可以进行加、减、乘、除、乘方运算,正数及零可以进行开平方运算,任意一个实数可以进行开立方运算.而且有理数的运算法则和运算律对于实数仍然适用.
进行新课
讨论 下列各式错在哪里
练一练:计算下列各式的值:
解:
解:
实数范围内的运算法则及运算顺序与有理数范围内是一样的.
归纳小结
例1 近似计算:
(1) (精确到0.01);
(2) (精确到0.1).
解:
在实数运算中,当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算.
归纳小结
例2 在数轴上作出表示下列各数的点,比较它们的大小,并用“<”连接它们.
2
-3
-2
-1
0
1
3
4
5
解:
由数轴上各点的位置,得
两个实数可以像有理数一样比较大小,即数轴上右边的点所表示的数总是大于左边的点所表示的数.在实数范围内也有:
正数大于零,负数小于零,正数大于负数.
两个正数,绝对值大的数较大.
两个负数,绝对值大的数反而小.
试一试
比较下列各组里两个数的大小:
随堂练习
1. 下列说法不正确的是( )
A.互为相反数的两个实数的和是有理数
B.互为倒数的两个实数的积是有理数
C.绝对值相等的两个实数的差是有理数
D.两个无理数的和可能是有理数
C
2. 计算:
(1) (精确到个位);
(2) (精确到 0.01).
11
2.58
3. 将下列各数表示在数轴上,并回答问题:
(1)将上面几个数用“<”连接起来;
(2)数轴上表示 和﹣2这两个数的点之间的距离是______.
4. 下列各数中,最小的数是( )
A.0 B.1 C.﹣1 D.
5. 介于 和 之间的整数是( )
A.2 B.3 C.4 D.5
6. 估计与0.5的大小关系是: ___ 0.5 .(填“>”“=”或“<”)
D
B
>
课堂小结
通过这节课的学习活动,你有什么收获?
课后作业
1.完成课本P16习题6.2第4,5题;
2.完成练习册本课时的习题。
