11.2.3三角形的外角 教案 人教版八年级数学上册
文档属性
| 名称 | 11.2.3三角形的外角 教案 人教版八年级数学上册 |  | |
| 格式 | docx | ||
| 文件大小 | 553.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 19:38:16 | ||
图片预览




文档简介
第十一章 三角形
·11.2与三角形有关的角·
第三课时 三角形的外角
教案
班级: 课时: 课型:
一、学情分析
学生在前面已经学习过“几何图形初步”和“相交线与平行线”,在此基础上,对三角形的外角进一步学习.三角形的外角性质在三角形的角度计算中有非常重要的桥梁作用,是三角形和四边形中进行角度推算的重要依据,在平面几何中有着重要的地位和作用.
二、教学目标
1.了解三角形外角的概念.
2.掌握三角形外角的性质的推理过程.
3.能综合利用三角形的内角和定理及外角的性质解决问题.
三、重点难点
【教学重点】
三角形的外角性质及应用.
【教学难点】
运用三角形外角性质进行有关计算时能准确地表达推理的过程.
四、教学过程设计
第一环节 【创设情境 引入新课】
课前热身:
1.三角形三个内角的和等于180°.
2.在△ABC中,(1)∠C = 90°,∠A = 30°,则∠B =60°;(2)∠A = 45°,∠B =∠C, 则∠B =67.5°.
3.在△ABC中,∠A:∠B:∠C = 2:3:4,则∠A =40°,∠B =60°,∠C =80°.
引入情境:
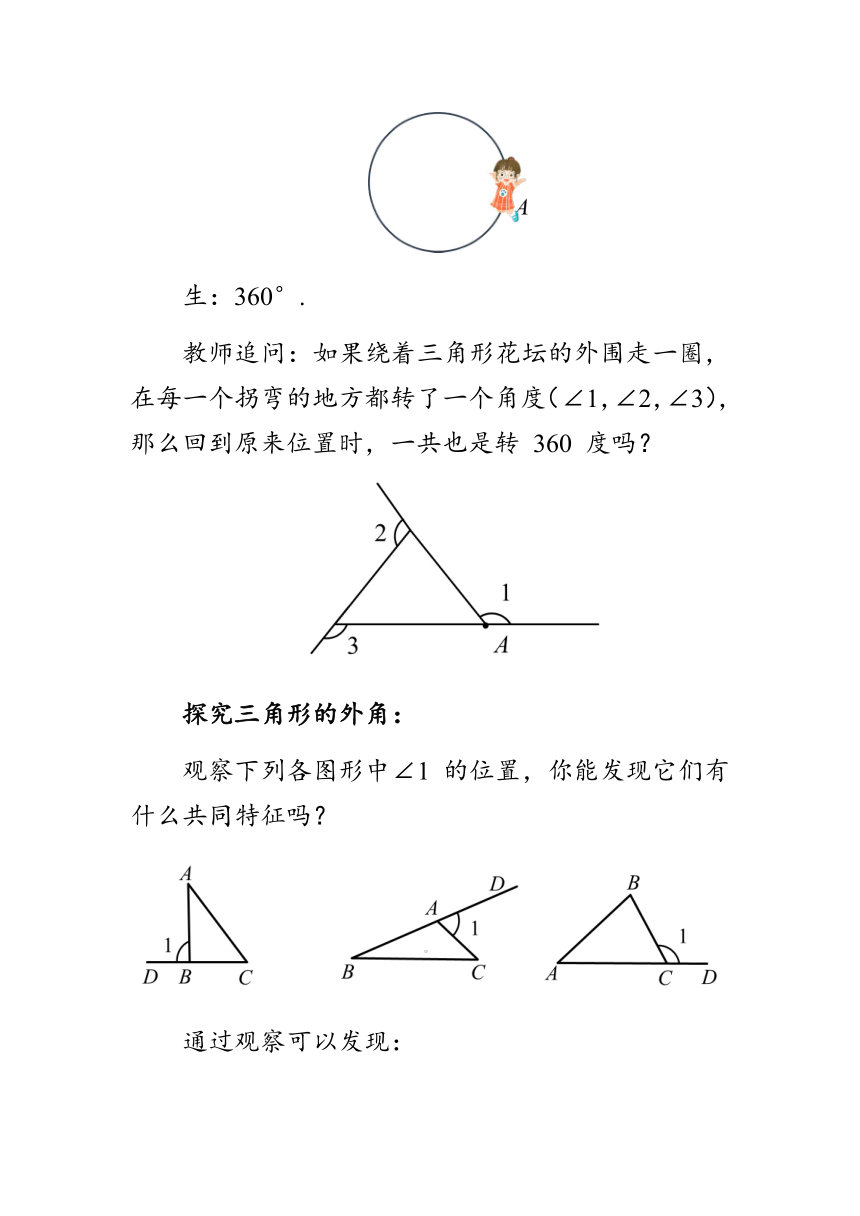
如图,小颖从点A出发,绕着圆形花坛的外围走一圈,那么回到原来位置时,一共转了多少度呢?
生:360°.
教师追问:如果绕着三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时,一共也是转 360 度吗?
探究三角形的外角:
观察下列各图形中∠1 的位置,你能发现它们有什么共同特征吗?
通过观察可以发现:
1.顶点是三角形的一个顶点;
2.一条边是三角形的一条边;
3.另一条边是三角形的一边的延长线.
由此可以得到三角形的外角的概念:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
教师让学生拿出准备好的练习本,在本上画出△ABC,然后画出它的所有外角,并探究如下问题:
1.每一个顶点处相对应的外角有几个?它们之间有什么关系?
2.三角形的每一个外角与相邻的内角有什么关系?
3.每一个三角形有几个外角?
(教师巡视课堂,适当提醒学生将三角形的边向两边延长即可画出三角形的所有外角.)
学生通过探究可以发现,三角形的每一个顶点处有 2 个互为对顶角的外角.并且每一个外角都与相邻的内角互为邻补角.一个三角形有6个外角,其中三个与另外三个分别相等.
巩固练习:
∠BEC是(△AEB)的外角,
也是(△BEC、△EFC)的内角.
∠BDC是(△BDC、△BDF)
的内角,也是(△ADC)的外角.
∠BFC是(△BDF 、△CEF)
的外角,也是(△BFC)的内角.
设计意图:通过探究,引导学生用已学知识感知三角形的外角,理解三角形的外角的概念.
第二环节 【合作交流 探索新知】
探究一:
如图,在△ABC中,∠A = 70 °,∠B = 60 °.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:由∠A +∠B +∠ACB = 180°,得∠ACB = 180°-∠A-∠B = 50°.
由∠ACB +∠ACD = 180°,得∠ACD = 180°-(180°-∠A-∠B)= ∠A +∠B = 130°.
教师追问:任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
师生进行探究,根据图形计算∠ACD的大小,通过计算,你发现了什么规律?
学生通过探究,发现∠ACD =∠A+∠B.
师生共同验证:∠ACD =∠A+∠B.
教师引导学生用文字总结:三角形的外角等于与它不相邻的两个内角的和.
探究二:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系
师生进行探究,最后得出:三角形的一个外角大于任何一个与它不相邻的内角.即∠ACD>∠A,∠ACD>∠B.
探究三:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
学生独立思考,教师引导学生用不用的解法进行探究(可以用三角形的内角和定理或三角形的外角的性质进行探究).
通过探究,学生得出它们的和为360°,用文字表述为:三角形的外角和是360°.
设计意图:通过计算、讨论、证明的方式探究三角形外角的性质及外角和,培养学生的合作交流和逻辑思维能力.
第三环节 【应用迁移 巩固提高】
例1.根据图所示,写出∠α的度数.
例2.如图,D是△ABC的边BC上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
(1)求∠B的度数;
(2)求∠C的度数.
例3.如图,直线AB∥CD,∠A = 70°,∠C = 40°,求∠E的度数.
设计意图:本环节结合新课知识对练习进行讲解,让学生学会运用三角形外角的性质及外角和进行解题.
【答案】
例1.解:①∠α = 25°+40°= 65°;
②∠α = 110°-35°= 75°;
③∠α = 40°+35°-60°= 15°;
④∠α = 180°-(360°-120°-108°)= 48°.
例2.解:(1)∵ ∠ADC是△ABD的外角,
∴ ∠ADC =∠B +∠BAD = 80°.
又∵ ∠B =∠BAD,
∴ ∠B = 80°×= 40°.
(2)在△ABC中,∠B+∠BAC+∠C = 180°,
由(1)得,∠B = 40°,
∴ ∠C = 180°-40°-70 °= 70°.
例3.解:如图所示,标出∠1和∠2.
∵ AB∥CD,
∠1 =∠A = 70°.
∴根据三角形外角性质,得
∠E =∠1-∠C = 70°- 40°= 30°.
第四环节 【随堂练习 巩固新知】
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.
(2)三角形的外角和等于它内角和的 2 倍.
(3)三角形的一个外角等于两个内角的和.
(4)三角形的一个外角等于与它不相邻的两个内角的和.
(5)三角形的一个外角大于任何一个内角.
(6)三角形的一个内角小于任何一个与它不相邻的外角.
2.(2019秋 达孜区期中)如图,∠1、∠2、∠3 中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
4.(2019春 平昌县期末)如图,∠A,∠1,∠2 的大小关系为( )
A.∠A>∠1>∠2 B.∠A>∠2>∠1
C.∠2>∠1>∠A D.∠2>∠A>∠1
5.(2019秋 文山市期末)如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A = 44°,∠1 = 57°,则∠2 = .
设计意图:本环节在于落实基础,通过解答简单练习,加强学生对新知识的理解.
【答案】
(1)×(2)√(3)×(4)√(5)×(6)√
C 3.C 4.C 5.101°
第五环节 【当堂检测 及时反馈】
1.(2019秋 新宾县期末)如图,BP是△ABC中∠ABC 的平分线,CP是∠ACB的外角的平分线,如果∠ABP = 20°,∠ACP = 50°,则∠A =( )
A.60° B.80° C.70° D.50°
2.(2019秋 路北区期末)如图,在△ABC中,∠A = 60 度,点D,E分别在AB,AC上,则∠1+∠2 的大小为多少度( )
A.140 B.190 C.320 D.240
3.(2019 枣庄)将一副直角三角板按如图所示的位置放置,使含 30°角的三角板的一条直角边和含 45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
4.(2019秋 织金县期末)如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2 =∠3+∠4 B.∠1+∠2 =∠4-∠3
C.∠1+∠4 =∠2+∠3 D.∠1+∠4 =∠2-∠3
5.(2019秋 蒙阴县期中)在△ABC中,∠A = 50°,∠B = 30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.60° B.10° C.45° D.10°或 60°
6.(2019秋 金凤区校级期末)如图,∠BCD = 150°,则∠A+∠B+∠D的度数为 .
7.有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F = 度.
8.求∠A +∠B +∠C +∠D +∠E的度数.
9.(2019秋 香洲区校级月考)一个零件的形状如图所示,按规定∠A = 90°,∠B和∠C分别是 32°和 21°的零件为合格零件,现质检工人量得∠BDC = 149°,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
10.(2019秋 汉滨区校级月考)已知:BP、CP是△ABC的外角的平分线,交于点P.求证:∠P = 90°- ∠A.
设计意图:通过本环节的练习,深化学生对知识的运用,同时提高学生的应用意识,掌握本课重难点.
【答案】
A 2.D 3.C 4.D 5.D
6.150° 7.360
8.解:∵ ∠1 是△FBE的外角,
∴ ∠1 =∠B+∠E.
同理∠2 =∠A+∠D,
在△CFG中∠C+∠1+∠2 = 180°,
∴ ∠A+∠B+∠C+∠D+∠E = 180°.
9.解:如图,延长BD交AC于E,
∵ ∠A = 90°,∠B = 32°,
∴ ∠DEC =∠A+∠B = 90°+32°= 122°,
∵ ∠C = 21°,
∴ ∠BDC =∠C +∠DEC = 21°+122°= 143°.
又∵ 质检工人量得∠BDC = 149°,
∴ 这个零件不合格.
10.证明:∵ BP、CP是△ABC的外角的平分线,
∴ ∠PCB =∠MCB,∠PBC =∠NBC,
∵ ∠MCB =∠A+∠ABC,∠NBC =∠A+∠ACB,
∴ ∠PCB+∠PBC =(∠A+∠ABC+∠A+∠ACB)= (180°+∠A)= 90°+ ∠A,
∴ ∠P = 180°-(∠PCB+∠PBC)= 180°﹣(90°+ ∠A)= 90°-∠A.
第六环节 【拓展延伸 能力提升】
1.如图,D、E分别在BC、AC上,AD、BE交于F.求证:
(1)∠AFB>∠C;
(2)∠AFB =∠1+∠2+∠C.
2.(2020秋 彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A = 50°,则∠D = ;
(2)若∠A = 80°,则∠D = ;
(3)若∠A = 130°,则∠D = ;
(4)若∠D = 36°,则∠A = ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
设计意图:本环节习题难度较高,考察学生能否灵活应用本课知识对综合问题进行求解,展现教学有梯度的理念.
【答案】
1.证明:(1)∵ ∠AFB是△AEF的一个外角,
∴ ∠AFB>∠AEF.
∵ ∠AEF是△BCE的一个外角,
∴ ∠AEF>∠C,∴ ∠AFB>∠C.
(2)∵ ∠AFB =∠AEB+∠1,
∠AEB =∠C+∠2,
∴ ∠AFB =∠1+∠C+∠2.
(1)25°,(2)40°,(3)65°,(4)72°,
(5)∠D =∠A.
理由如下:∵ BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴ ∠ACE = 2∠2,∠ABC = 2∠1,
∵ ∠ACE =∠ABC+∠A,
∴ 2∠2 = 2∠1+∠A,
而∠2 =∠1+∠D,
∴ 2∠2 = 2∠1+2∠D,
∴ ∠A = 2∠D,
即∠D =∠A.
第七环节 【总结反思 知识内化】
课堂小结:
三角形内角和外角的性质:
1.三角形的内角和等于 180°.
2.三角形的一个外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角.
(2)三角形的一个外角等于与它不相邻的两个内角的和.
(3)三角形的一个外角大于任何一个与它不相邻的内角.
3.三角形的外角的和等于 360°.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
·11.2与三角形有关的角·
第三课时 三角形的外角
教案
班级: 课时: 课型:
一、学情分析
学生在前面已经学习过“几何图形初步”和“相交线与平行线”,在此基础上,对三角形的外角进一步学习.三角形的外角性质在三角形的角度计算中有非常重要的桥梁作用,是三角形和四边形中进行角度推算的重要依据,在平面几何中有着重要的地位和作用.
二、教学目标
1.了解三角形外角的概念.
2.掌握三角形外角的性质的推理过程.
3.能综合利用三角形的内角和定理及外角的性质解决问题.
三、重点难点
【教学重点】
三角形的外角性质及应用.
【教学难点】
运用三角形外角性质进行有关计算时能准确地表达推理的过程.
四、教学过程设计
第一环节 【创设情境 引入新课】
课前热身:
1.三角形三个内角的和等于180°.
2.在△ABC中,(1)∠C = 90°,∠A = 30°,则∠B =60°;(2)∠A = 45°,∠B =∠C, 则∠B =67.5°.
3.在△ABC中,∠A:∠B:∠C = 2:3:4,则∠A =40°,∠B =60°,∠C =80°.
引入情境:
如图,小颖从点A出发,绕着圆形花坛的外围走一圈,那么回到原来位置时,一共转了多少度呢?
生:360°.
教师追问:如果绕着三角形花坛的外围走一圈,在每一个拐弯的地方都转了一个角度(∠1,∠2,∠3),那么回到原来位置时,一共也是转 360 度吗?
探究三角形的外角:
观察下列各图形中∠1 的位置,你能发现它们有什么共同特征吗?
通过观察可以发现:
1.顶点是三角形的一个顶点;
2.一条边是三角形的一条边;
3.另一条边是三角形的一边的延长线.
由此可以得到三角形的外角的概念:
三角形的一边与另一边的延长线组成的角,叫做三角形的外角.
教师让学生拿出准备好的练习本,在本上画出△ABC,然后画出它的所有外角,并探究如下问题:
1.每一个顶点处相对应的外角有几个?它们之间有什么关系?
2.三角形的每一个外角与相邻的内角有什么关系?
3.每一个三角形有几个外角?
(教师巡视课堂,适当提醒学生将三角形的边向两边延长即可画出三角形的所有外角.)
学生通过探究可以发现,三角形的每一个顶点处有 2 个互为对顶角的外角.并且每一个外角都与相邻的内角互为邻补角.一个三角形有6个外角,其中三个与另外三个分别相等.
巩固练习:
∠BEC是(△AEB)的外角,
也是(△BEC、△EFC)的内角.
∠BDC是(△BDC、△BDF)
的内角,也是(△ADC)的外角.
∠BFC是(△BDF 、△CEF)
的外角,也是(△BFC)的内角.
设计意图:通过探究,引导学生用已学知识感知三角形的外角,理解三角形的外角的概念.
第二环节 【合作交流 探索新知】
探究一:
如图,在△ABC中,∠A = 70 °,∠B = 60 °.∠ACD是△ABC的一个外角.能由∠A,∠B求出∠ACD吗?如果能,∠ACD与∠A,∠B有什么关系?
解:由∠A +∠B +∠ACB = 180°,得∠ACB = 180°-∠A-∠B = 50°.
由∠ACB +∠ACD = 180°,得∠ACD = 180°-(180°-∠A-∠B)= ∠A +∠B = 130°.
教师追问:任意一个三角形的一个外角与它不相邻的两个内角是否都有这种关系?
师生进行探究,根据图形计算∠ACD的大小,通过计算,你发现了什么规律?
学生通过探究,发现∠ACD =∠A+∠B.
师生共同验证:∠ACD =∠A+∠B.
教师引导学生用文字总结:三角形的外角等于与它不相邻的两个内角的和.
探究二:三角形的一个外角与它不相邻的任意一个内角有怎样的大小关系
师生进行探究,最后得出:三角形的一个外角大于任何一个与它不相邻的内角.即∠ACD>∠A,∠ACD>∠B.
探究三:如图,∠BAE,∠CBF,∠ACD是△ABC的三个外角,它们的和是多少?
学生独立思考,教师引导学生用不用的解法进行探究(可以用三角形的内角和定理或三角形的外角的性质进行探究).
通过探究,学生得出它们的和为360°,用文字表述为:三角形的外角和是360°.
设计意图:通过计算、讨论、证明的方式探究三角形外角的性质及外角和,培养学生的合作交流和逻辑思维能力.
第三环节 【应用迁移 巩固提高】
例1.根据图所示,写出∠α的度数.
例2.如图,D是△ABC的边BC上一点,∠B =∠BAD,∠ADC = 80°,∠BAC = 70°.
(1)求∠B的度数;
(2)求∠C的度数.
例3.如图,直线AB∥CD,∠A = 70°,∠C = 40°,求∠E的度数.
设计意图:本环节结合新课知识对练习进行讲解,让学生学会运用三角形外角的性质及外角和进行解题.
【答案】
例1.解:①∠α = 25°+40°= 65°;
②∠α = 110°-35°= 75°;
③∠α = 40°+35°-60°= 15°;
④∠α = 180°-(360°-120°-108°)= 48°.
例2.解:(1)∵ ∠ADC是△ABD的外角,
∴ ∠ADC =∠B +∠BAD = 80°.
又∵ ∠B =∠BAD,
∴ ∠B = 80°×= 40°.
(2)在△ABC中,∠B+∠BAC+∠C = 180°,
由(1)得,∠B = 40°,
∴ ∠C = 180°-40°-70 °= 70°.
例3.解:如图所示,标出∠1和∠2.
∵ AB∥CD,
∠1 =∠A = 70°.
∴根据三角形外角性质,得
∠E =∠1-∠C = 70°- 40°= 30°.
第四环节 【随堂练习 巩固新知】
1.判断题:
(1)三角形的外角和是指三角形所有外角的和.
(2)三角形的外角和等于它内角和的 2 倍.
(3)三角形的一个外角等于两个内角的和.
(4)三角形的一个外角等于与它不相邻的两个内角的和.
(5)三角形的一个外角大于任何一个内角.
(6)三角形的一个内角小于任何一个与它不相邻的外角.
2.(2019秋 达孜区期中)如图,∠1、∠2、∠3 中是△ABC外角的是( )
A.∠1、∠2 B.∠2、∠3
C.∠1、∠3 D.∠1、∠2、∠3
3.若一个三角形的一个外角小于与它相邻的内角,则这个三角形是( )
A.直角三角形 B.锐角三角形
C.钝角三角形 D.无法确定
4.(2019春 平昌县期末)如图,∠A,∠1,∠2 的大小关系为( )
A.∠A>∠1>∠2 B.∠A>∠2>∠1
C.∠2>∠1>∠A D.∠2>∠A>∠1
5.(2019秋 文山市期末)如图,在△ABC中,D、E分别是AB、AC上的点,点F在BC的延长线上,DE∥BC,∠A = 44°,∠1 = 57°,则∠2 = .
设计意图:本环节在于落实基础,通过解答简单练习,加强学生对新知识的理解.
【答案】
(1)×(2)√(3)×(4)√(5)×(6)√
C 3.C 4.C 5.101°
第五环节 【当堂检测 及时反馈】
1.(2019秋 新宾县期末)如图,BP是△ABC中∠ABC 的平分线,CP是∠ACB的外角的平分线,如果∠ABP = 20°,∠ACP = 50°,则∠A =( )
A.60° B.80° C.70° D.50°
2.(2019秋 路北区期末)如图,在△ABC中,∠A = 60 度,点D,E分别在AB,AC上,则∠1+∠2 的大小为多少度( )
A.140 B.190 C.320 D.240
3.(2019 枣庄)将一副直角三角板按如图所示的位置放置,使含 30°角的三角板的一条直角边和含 45°角的三角板的一条直角边放在同一条直线上,则∠α的度数是( )
A.45° B.60° C.75° D.85°
4.(2019秋 织金县期末)如图,∠1,∠2,∠3,∠4恒满足关系式是( )
A.∠1+∠2 =∠3+∠4 B.∠1+∠2 =∠4-∠3
C.∠1+∠4 =∠2+∠3 D.∠1+∠4 =∠2-∠3
5.(2019秋 蒙阴县期中)在△ABC中,∠A = 50°,∠B = 30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为( )
A.60° B.10° C.45° D.10°或 60°
6.(2019秋 金凤区校级期末)如图,∠BCD = 150°,则∠A+∠B+∠D的度数为 .
7.有一次小明看见这样一个图,要计算:∠A+∠B+∠C+∠D+∠E+∠F = 度.
8.求∠A +∠B +∠C +∠D +∠E的度数.
9.(2019秋 香洲区校级月考)一个零件的形状如图所示,按规定∠A = 90°,∠B和∠C分别是 32°和 21°的零件为合格零件,现质检工人量得∠BDC = 149°,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
10.(2019秋 汉滨区校级月考)已知:BP、CP是△ABC的外角的平分线,交于点P.求证:∠P = 90°- ∠A.
设计意图:通过本环节的练习,深化学生对知识的运用,同时提高学生的应用意识,掌握本课重难点.
【答案】
A 2.D 3.C 4.D 5.D
6.150° 7.360
8.解:∵ ∠1 是△FBE的外角,
∴ ∠1 =∠B+∠E.
同理∠2 =∠A+∠D,
在△CFG中∠C+∠1+∠2 = 180°,
∴ ∠A+∠B+∠C+∠D+∠E = 180°.
9.解:如图,延长BD交AC于E,
∵ ∠A = 90°,∠B = 32°,
∴ ∠DEC =∠A+∠B = 90°+32°= 122°,
∵ ∠C = 21°,
∴ ∠BDC =∠C +∠DEC = 21°+122°= 143°.
又∵ 质检工人量得∠BDC = 149°,
∴ 这个零件不合格.
10.证明:∵ BP、CP是△ABC的外角的平分线,
∴ ∠PCB =∠MCB,∠PBC =∠NBC,
∵ ∠MCB =∠A+∠ABC,∠NBC =∠A+∠ACB,
∴ ∠PCB+∠PBC =(∠A+∠ABC+∠A+∠ACB)= (180°+∠A)= 90°+ ∠A,
∴ ∠P = 180°-(∠PCB+∠PBC)= 180°﹣(90°+ ∠A)= 90°-∠A.
第六环节 【拓展延伸 能力提升】
1.如图,D、E分别在BC、AC上,AD、BE交于F.求证:
(1)∠AFB>∠C;
(2)∠AFB =∠1+∠2+∠C.
2.(2020秋 彭水县校级月考)如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的外角平分线,CD与BD交于点D.
(1)若∠A = 50°,则∠D = ;
(2)若∠A = 80°,则∠D = ;
(3)若∠A = 130°,则∠D = ;
(4)若∠D = 36°,则∠A = ;
(5)综上所述,你会得到什么结论?证明你的结论的准确性.
设计意图:本环节习题难度较高,考察学生能否灵活应用本课知识对综合问题进行求解,展现教学有梯度的理念.
【答案】
1.证明:(1)∵ ∠AFB是△AEF的一个外角,
∴ ∠AFB>∠AEF.
∵ ∠AEF是△BCE的一个外角,
∴ ∠AEF>∠C,∴ ∠AFB>∠C.
(2)∵ ∠AFB =∠AEB+∠1,
∠AEB =∠C+∠2,
∴ ∠AFB =∠1+∠C+∠2.
(1)25°,(2)40°,(3)65°,(4)72°,
(5)∠D =∠A.
理由如下:∵ BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,
∴ ∠ACE = 2∠2,∠ABC = 2∠1,
∵ ∠ACE =∠ABC+∠A,
∴ 2∠2 = 2∠1+∠A,
而∠2 =∠1+∠D,
∴ 2∠2 = 2∠1+2∠D,
∴ ∠A = 2∠D,
即∠D =∠A.
第七环节 【总结反思 知识内化】
课堂小结:
三角形内角和外角的性质:
1.三角形的内角和等于 180°.
2.三角形的一个外角的性质
(1)三角形的一个外角与它相邻内角的关系是互为邻补角.
(2)三角形的一个外角等于与它不相邻的两个内角的和.
(3)三角形的一个外角大于任何一个与它不相邻的内角.
3.三角形的外角的和等于 360°.
设计意图:通过知识小结,使学生梳理本节课所学内容,理解本课核心知识,提高学习质量.
第八环节 【布置作业 夯实基础】
