解直角三角形及其应用

浅谈初中数学总复习课堂中学生发散性思维的培养 教案：解直角三角形及其应用
解直角三角形及其应用
湖南省安仁县清溪中学 谭澜
【大纲要求及知识目标】掌握三角函数的简单应用。
【能力目标】1、培养学生理解概念，并能熟练掌握并且加以运用的能力；
2、培养学生把实际问题转化为数学问题并进行解决的能力，进而提高学生形象思维能力；渗透转化的思想。
【情感目标】培养学生理论联系实际，敢于实践，勇于探索的精神。
【知识点】1、直角三角形中各元素之间的关系；
2、 仰角、俯角、坡角、坡度、方位角等概念；
3、 解直角三角形；
4、 解直角三角形的应用。
【教学重点与难点】解直角三角形及其应用
【教学过程】
1、 课堂引入：
（大概用1分钟）
同学们，我们知道数学来源于生活同时又反过来服务于生活，本节课在锐角三角函数的基本概念和性质的基础之上，让我们来继续复习锐角三角函数这一章的第二部分—— “解直角三角形及其应用”，真切去感受数学知识带给我们的乐趣与成就感！（板书课题：解直角三角形及其应用）
“万丈高楼平地起”，首先请同学们独立完成预习练习，让我们为接下来的应用打下良好而坚实的基础吧！
二、预习练习：
（先让学生花10分钟左右的时间予以独立完成，可采取分组解答进行比赛的形式，再由教师与学生一起用5分钟的时间进行核对答案和归纳）
1、在RtΔABC中，∠C=90 ，∠A、∠B、∠C所对的边之长分别为a,b,c.
（1）边边关系：（勾股定理）：a2+b2=c2
（2）角角关系：（两锐角互余）：∠A+∠B=90
（3）边角关系：（满足锐角三角函数关系）
； ； .
2、在直角三角形中，除直角外的5个元素（3条边和2个锐角），只要知道其中的2个元素（至少有一个是边），利用边角之间的关系，就可以求出其余的3个未知元素，这叫作解直角三角形。
3、△ABC中，∠C＝90°，根据表中的数据求其它元素的值：
b c ∠A ∠B
6 6 12 30° 60
4 4 4 45 45°
5 5 10 60 30
4 4 8 45 45
（归纳概括：解直角三角形的四种基本题型＜简要板书＞
结合上表，填写好下列各题的的空格：
（口诀：有弦用弦，无弦用切；宁乘毋除，取原避中。＜板书＞）
在RtΔABC中，∠C=90 ，AB=c,BC=a,AC=b.
①已知斜边（c）和一锐角(∠A),求两直角边（a,b）和另一锐角（∠B）.
方法：先由∠A+∠B=90 求出∠B的度数；再由求出a边的长；
最后由a2+b2=c2求出b的长度。
②已知一直角边（b）和一锐角(∠B),
求另一直角边（a）、斜边（c）及另一锐角（∠A）.
方法：先由∠A+∠B=90 求出∠A的度数；再由求出c边的长，
最后由a2+b2=c2求出a的长度。
③已知两直角边(a,b),求斜边(c)及两个锐角(∠A、∠B).
方法：先由a2+b2=c2求出c的长度，再由求出∠A的度数，
最后由∠A+∠B=90 求出∠B的度数。
④已知一直角边（b）和斜边(c),求另一直角边（a）及两锐角（∠A、∠B）.
方法：先由a2+b2=c2求出a的长度，再由求出∠B的度数，
最后由∠A+∠B=90 求出∠A的度数。
4、填空：
（1）视线与水平线所成的锐角中，视线在水平线上方的角叫做仰角，视线在水平线下方的角叫做俯角。请在下图中相应的位置分别标明“仰角” 和“俯角”
字样。
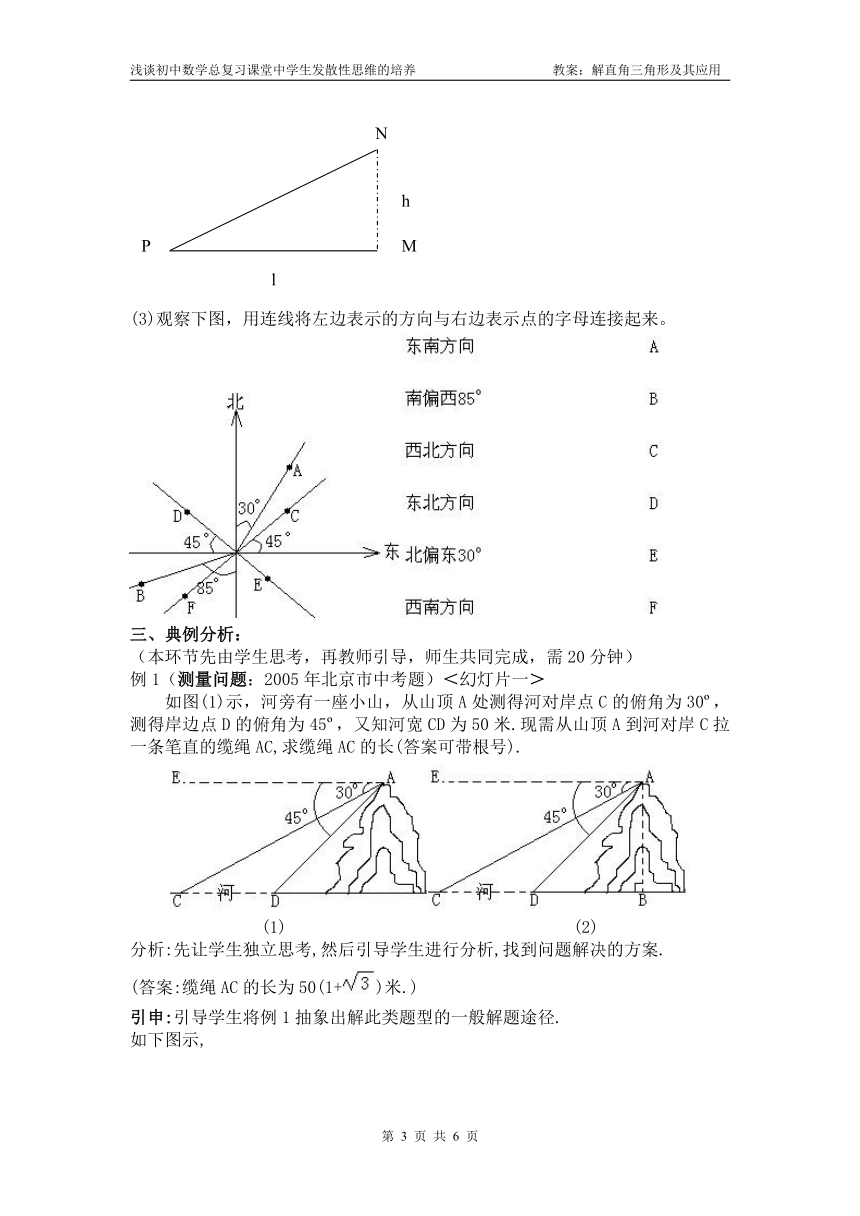
（2）如图示，从山脚下点P上坡走到点N时，升高的高度h(即线段MN的长)与水平前进的距离l（即线段PM的长度）的比叫做坡度，用字母i表示，即.坡度通常写成1：m的形式.图中的∠MPN叫作坡角（即山坡与地平面的夹角）.显然，坡度等于坡角的正切。坡度越大，山坡越陡。
(3)观察下图，用连线将左边表示的方向与右边表示点的字母连接起来。
三、典例分析：
（本环节先由学生思考，再教师引导，师生共同完成，需20分钟）
例1（测量问题：2005年北京市中考题）＜幻灯片一＞
如图(1)示，河旁有一座小山，从山顶A处测得河对岸点C的俯角为30 ，测得岸边点D的俯角为45 ，又知河宽CD为50米.现需从山顶A到河对岸C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号).
(1) (2)
分析:先让学生独立思考,然后引导学生进行分析,找到问题解决的方案.
(答案:缆绳AC的长为50(1+)米.)
引申:引导学生将例1抽象出解此类题型的一般解题途径.
如下图示,
思维拓展一：
例2(航海问题:2005年天津市中考题) ＜幻灯片一＞
如图示,一艘货轮向正北方向航行,在点A处测得灯塔M在北偏西30 ,货轮以每小时20海里的速度航行,1小时后到达B处,测得灯塔M在北偏西45 ,问该货轮到达灯塔正东方向D处时,货轮与灯塔M的距离是多少
(精确到0.1海里,≈1.732)
分析:先让学生独立思考,然后教师从方位角等概念入手，引导学生进行探求解决。在解决本题之后，还可引导学生将航海问题与测量问题进行类比分析,从而得出与之相似的结论，从而可将此种类型的航海问题与测量问题合二为一，达到触类旁通的效果. (答案:约为27.3海里)
思维拓展二：
例3（坡度问题：2005年哈尔滨市中考题）＜幻灯片二＞
如图示，拦水坝的横断面为梯形ABCD，坝顶宽BC为6m,坝高为3.2m.为了提高水坝的拦水能力，需要将水坝加高2m,并且保持坝顶宽度不变，迎水坡CD的坡度不变，但是背水坡的坡度由原来的i=1:2变成i'=1:2.5，（有关数据在图上已注明）.求加高后的坝底HD的长为多少？
分析：先由学生独立思考，然后从坡度、坡角的基本概念入手，引导学生作出相关的辅助线，最后将其解答出来。
（答案：加高后的坝底HD的长为29.4m）
思维拓展三：
例4（方案设计题：2005年沈阳市中考题）＜幻灯片三＞
如图示，A、B为两个村庄，AB、BC、CD为公路，BD为田地，AD为河宽，且CD与AD互相垂直.现在要从点E处开始铺设通往村庄A、村庄B的一条电缆，共有如下两种铺设方案：
方案一：E→D→A→B；方案二：E→C→B→A.
经测量得AB=4千米，BC=10千米，CE=6千米，∠BDC=45 ，∠ABD=15 .
已知：地下电缆的修建费为2万元/千米，水下电缆的修建费为4万元/千米.
(1)求出河宽AD（结果保留根号）；
(2)求出公路CD的长；
(3)哪种方案铺设电缆的费用低？请说明你的理由.
分析：本题为方案设计题，这是近年中考中的一个新题型，也是一个热点题型，要求学生具有比较周全的逻辑思维能力和分析能力。
四、沙场练兵：（先学生独立完成，再师生共同核对答案，大概需要10分钟）
1.如图，某海埂的横断面是梯形，坎上底AD为4米，近水面（斜坡AB）的坡度i=1：，斜坡AB的长度为12米，背水面（斜坡CD）的坡度为i=1：1，求（1）斜坡AB的坡角（2）坎底宽BC和斜坡CD的长。
2.要测得底部不能到达的烟囱的高AB，从与烟囱底部在同一水平线的C、D两处测得烟囱的仰角为α、β，CD间的距离是a米，已知测角仪的高b米，求烟囱的高AB
3.一船从西向东航行，航行到灯塔C处，测得海岛B在北偏东60°方向，该船继续向东航行到达灯塔D处时，测得海岛B在北偏东45°方向，若灯塔C、D间的距离是10海里，海岛B周围12海里有暗礁，问该船继续航行（沿原方向）有无触礁的危险？
五、课堂小结：（1分钟）
1、直角三角形中除直角外的五元素之间的关系；
2、仰角、俯角、坡角、坡度、方位角等概念；
3、解直角三角形的定义及四种基本题型；
4、解直角三角形的四种基本应用：
（1）测量问题；（2）航海问题；（3）坡度问题；（4）方案设计问题。
附：板书设计
解直角三角形及其应用
一、解直角三角形（左版上）
1、直角三角形中各元素之间的关系
（1） 边边关系：a2+b2=c2
（2） 角角关系：∠A+∠B=90
（3） 边角关系：满足三角函数关系
2、解直角三角形的定义
3、解直角三角形的四种基本题型
口诀：有弦用弦，无弦用切；宁乘毋除，取原避中。
二、解直角三角形的应用（左版下）
1、常用概念
（1）仰角与俯角
（2）坡角、坡度
（3）方位角
2、四种基本应用（中版上）
例1：（测量问题）（中版上）
例2：（航海问题）（中版下）
例3：（坡度问题）（右版上）
例4：（方案设计题）（右版下）
水平线
视线
视线
铅垂线
l
h
M
P
N
第 3 页 共 6 页