1.2.2 加减消元法(第1课时) 课件(共16张PPT)-2023-2024学年湘教版数学七年级下册
文档属性
| 名称 | 1.2.2 加减消元法(第1课时) 课件(共16张PPT)-2023-2024学年湘教版数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-21 20:19:53 | ||
图片预览





文档简介
(共16张PPT)
加减消元法
湘教版·七年级数学下册
①
复习导入
解二元一次方程组的基本想法是:__________________________
___________________________________________________
消去一个未知数(简称为消元),
得到一个一元一次方程,
然后解这个一元一次方程.
关键
把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法
叫做代入消元法.简称代入法.
探究新知
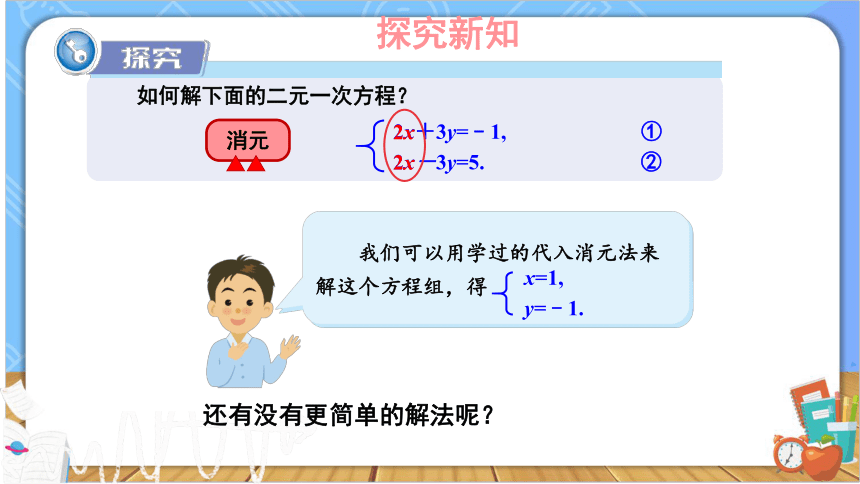
如何解下面的二元一次方程?
2x+3y=﹣1, ①
2x-3y=5. ②
我们可以用学过的代入消元法来解这个方程组,得
x=1,
y=﹣1.
还有没有更简单的解法呢?
消元
2x
2x
探究新知
如何解下面的二元一次方程?
2x+3y=﹣1, ①
2x-3y=5. ②
消元
2x
2x
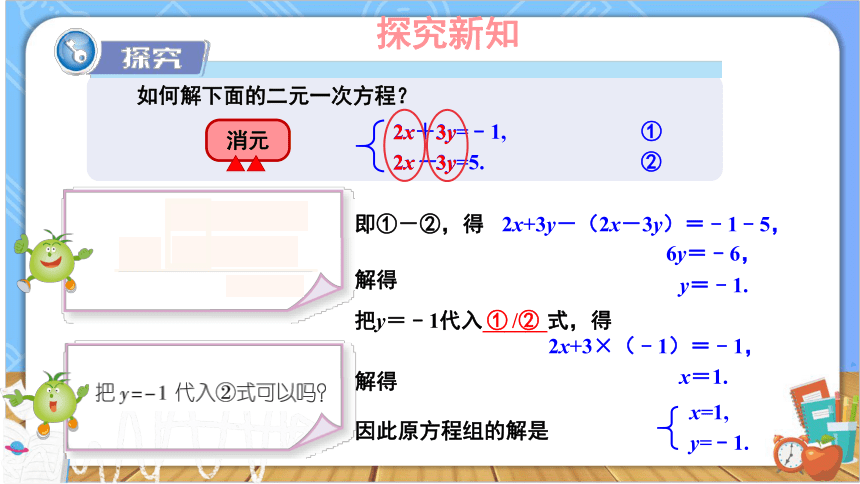
即①-②,得
2x+3y-(2x-3y)=﹣1﹣5,
6y=﹣6,
解得
y=﹣1.
把y=﹣1代入______式,得
①
/②
2x+3×(﹣1)=﹣1,
解得
x=1.
因此原方程组的解是
x=1,
y=﹣1.
3y
3y
探究新知
2x+3y=﹣1, ①
2x-3y=5. ②
消元
3y
3y
在消元过程中,如果把方程①与方程②相加,可以消去一个未知数吗?
如何解下面的二元一次方程?
即①+②,得
2x+3y+(2x-3y)=﹣1+5,
4x=4,
解得
x=1.
把x=1代入______式,得
①
/②
2×1+3y=﹣1,
解得
y=﹣1.
因此原方程组的解是
x=1,
y=﹣1.
探究新知
例 3
解二元一次方程组:
7x+3y=1, ①
2x-3y=8. ②
3y
3y
解:①+②,得
7x+3y+(2x-3y)=1+8,
9x=9,
解得
x=1.
把x=1代入①式,得
7×1+3y=1,
解得
y=﹣2.
因此原方程组的解是
x=1,
y=﹣2.
【归纳结论】两个二元一次方程中同一未知数的系数相同或相反时,把这两个方程相减或相加,就能消去这个未知数,从而得到一个一元一次方程,这种解方程组的方法叫做加减消元法,简称加减法.
2x+3y=﹣1, ①
2x-3y=5. ②
解:即①-②,得
2x+3y-(2x-3y)=﹣1-5,
解:①+②,得
7x+3y+(2x-3y)=1+8,
2x+3y=﹣1, ①
2x-3y=5. ②
解:即①+②,得
2x+3y+(2x-3y)=﹣1+5,
7x+3y=1, ①
2x-3y=8. ②
例 3
3y
3y
探究新知
用加减法解二元一次方程组的时候,什么条件下用加法?什么条件下用减法?
2x
2x
3y
3y
【归纳结论】 当方程组中同一未知数的系数互为相反数时,我们可以把两方程相加,当方程组中同一未知数的系数相等时,我们可以把两方程相减,从而达到消元的目的.
探究新知
例 4
解二元一次方程组:
2x+3y=﹣11, ①
6x-5y=9. ②
能直接相加减消掉一个未知数吗?
如何把同一未知数的系数变成一样呢?
②-③,得
-14y=42,
解得
y=﹣3.
把y=﹣3代入①式,得
2x+3×(﹣3)=﹣11,
解得
x=﹣1.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①×3,得
6x+9y=﹣33, ③
在例4中,如果先消去y应该如何解?会与上述结果一致吗?
2x+3y=﹣11, ①
6x-5y=9. ②
②+③,得
解得
x=﹣1.
把x=﹣1代入①式,得
2×(﹣1)+3y=﹣11,
解得
y=﹣3.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①× ,得
x+5y=﹣ , ③
x= ,
巩固练习
用加减法解二元一次方程组:
[选自教材P10 练习]
2x+y=﹣2, ①
﹣2x+3y=18; ②
(1)
5a-2b=11, ①
5a+3b=﹣4; ②
(2)
解:①+②,得
2x+y+(﹣2x+3y)=﹣2+18,
4y=16,
解得
y=4.
把y=4代入①式,得
2x+4=﹣2,
解得
x=﹣3.
因此原方程组的解是
x=﹣3,
y=4.
解:①-②,得
5a-2b-(5a+3b)=11-(﹣4),
﹣5b=15,
解得
b=﹣3.
把b=﹣3代入②式,得
5a+3×(﹣3)=﹣4,
解得
a=1.
因此原方程组的解是
a=1,
b=﹣3.
3m+2n=8, ①
6m-5n=﹣47; ②
(3)
2x-4y=34, ①
5x+2y=31; ②
(4)
③-②,得
9n=63,
解得
n=7.
把n=7代入①式,得
3m+2×7=8,
解得
m=﹣2.
因此原方程组的解是
m=﹣2,
n=7.
解:①×2,得
6m+4n=16, ③
③+②,得
12x=96,
解得
x=8.
把x=8代入①式,得
2×8-4y=34,
解得
因此原方程组的解是
解:②×2,得
10x+4y=62, ③
y=﹣ .
x=8,
y=﹣ .
巩固练习
[选自教材P10 练习]
2.解下列二元一次方程组:
2(x+2y)-5y=﹣1, ①
3(x-y)+y=2; ②
(1)
, ①
; ②
(2)
③-②,得
x=﹣4,
把x=﹣4代入③式,得
2×(﹣4)-y=34,
解得
因此原方程组的解是
①×2,得
2x-y=﹣2, ③
y=﹣7.
x=﹣4,
y=﹣7.
解:化简得
2x-y=﹣1, ①
3x-2y=2; ②
解:①+②,得
y=﹣9,
解得
把y=﹣9代入②式,得
解得
x=6.
因此原方程组的解是
x=6,
y=﹣9.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
m+2n+5=0, ①
7m-2n-13=0; ②
(3)
2x+5y=0, ①
x+3y=1; ②
(4)
解:①+②,得
m=1,
解得
把m=1代入①式,得
解得
n=﹣3.
因此原方程组的解是
m=1,
n=﹣3.
m+7m+5-13=0,
1+2n+5=0,
③-①,得
y=2,
把y=2代入③式,得
2x+6×2=2,
解得
因此原方程组的解是
解:②×2,得
2x+6y=2, ③
x=﹣5.
x=﹣5,
y=2.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
2x-y=3, ①
4x+3y=﹣13; ②
(5)
1.5p-2q=﹣1, ①
﹣4.5p+7q=8; ②
(6)
③-②,得
解得
因此原方程组的解是
解:①×2,得
4x-2y=6, ③
﹣2y-3y=6-(﹣13),
解得
y=﹣ ,
把y=﹣ 代入①式,得
2x-(﹣ )=3,
x=﹣ .
x=﹣ ,
y= ﹣ .
③+②,得
q=5,
把q=5代入①式,得
1.5p-2×5=2,
解得
因此原方程组的解是
解:①×3,得
4.5p-6q=﹣3, ③
p=6.
p=6,
q=5.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
课堂小结
代入消元法
加减消元法
解一元一次方程
二元一次方
程组的解法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
加减消元法
湘教版·七年级数学下册
①
复习导入
解二元一次方程组的基本想法是:__________________________
___________________________________________________
消去一个未知数(简称为消元),
得到一个一元一次方程,
然后解这个一元一次方程.
关键
把其中一个方程的某一个未知数用含有另一个未知数的代数式表示,然后把它代入到另一个方程中,便得到一个一元一次方程.这种解方程组的方法
叫做代入消元法.简称代入法.
探究新知
如何解下面的二元一次方程?
2x+3y=﹣1, ①
2x-3y=5. ②
我们可以用学过的代入消元法来解这个方程组,得
x=1,
y=﹣1.
还有没有更简单的解法呢?
消元
2x
2x
探究新知
如何解下面的二元一次方程?
2x+3y=﹣1, ①
2x-3y=5. ②
消元
2x
2x
即①-②,得
2x+3y-(2x-3y)=﹣1﹣5,
6y=﹣6,
解得
y=﹣1.
把y=﹣1代入______式,得
①
/②
2x+3×(﹣1)=﹣1,
解得
x=1.
因此原方程组的解是
x=1,
y=﹣1.
3y
3y
探究新知
2x+3y=﹣1, ①
2x-3y=5. ②
消元
3y
3y
在消元过程中,如果把方程①与方程②相加,可以消去一个未知数吗?
如何解下面的二元一次方程?
即①+②,得
2x+3y+(2x-3y)=﹣1+5,
4x=4,
解得
x=1.
把x=1代入______式,得
①
/②
2×1+3y=﹣1,
解得
y=﹣1.
因此原方程组的解是
x=1,
y=﹣1.
探究新知
例 3
解二元一次方程组:
7x+3y=1, ①
2x-3y=8. ②
3y
3y
解:①+②,得
7x+3y+(2x-3y)=1+8,
9x=9,
解得
x=1.
把x=1代入①式,得
7×1+3y=1,
解得
y=﹣2.
因此原方程组的解是
x=1,
y=﹣2.
【归纳结论】两个二元一次方程中同一未知数的系数相同或相反时,把这两个方程相减或相加,就能消去这个未知数,从而得到一个一元一次方程,这种解方程组的方法叫做加减消元法,简称加减法.
2x+3y=﹣1, ①
2x-3y=5. ②
解:即①-②,得
2x+3y-(2x-3y)=﹣1-5,
解:①+②,得
7x+3y+(2x-3y)=1+8,
2x+3y=﹣1, ①
2x-3y=5. ②
解:即①+②,得
2x+3y+(2x-3y)=﹣1+5,
7x+3y=1, ①
2x-3y=8. ②
例 3
3y
3y
探究新知
用加减法解二元一次方程组的时候,什么条件下用加法?什么条件下用减法?
2x
2x
3y
3y
【归纳结论】 当方程组中同一未知数的系数互为相反数时,我们可以把两方程相加,当方程组中同一未知数的系数相等时,我们可以把两方程相减,从而达到消元的目的.
探究新知
例 4
解二元一次方程组:
2x+3y=﹣11, ①
6x-5y=9. ②
能直接相加减消掉一个未知数吗?
如何把同一未知数的系数变成一样呢?
②-③,得
-14y=42,
解得
y=﹣3.
把y=﹣3代入①式,得
2x+3×(﹣3)=﹣11,
解得
x=﹣1.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①×3,得
6x+9y=﹣33, ③
在例4中,如果先消去y应该如何解?会与上述结果一致吗?
2x+3y=﹣11, ①
6x-5y=9. ②
②+③,得
解得
x=﹣1.
把x=﹣1代入①式,得
2×(﹣1)+3y=﹣11,
解得
y=﹣3.
因此原方程组的解是
x=﹣1,
y=﹣3.
解:①× ,得
x+5y=﹣ , ③
x= ,
巩固练习
用加减法解二元一次方程组:
[选自教材P10 练习]
2x+y=﹣2, ①
﹣2x+3y=18; ②
(1)
5a-2b=11, ①
5a+3b=﹣4; ②
(2)
解:①+②,得
2x+y+(﹣2x+3y)=﹣2+18,
4y=16,
解得
y=4.
把y=4代入①式,得
2x+4=﹣2,
解得
x=﹣3.
因此原方程组的解是
x=﹣3,
y=4.
解:①-②,得
5a-2b-(5a+3b)=11-(﹣4),
﹣5b=15,
解得
b=﹣3.
把b=﹣3代入②式,得
5a+3×(﹣3)=﹣4,
解得
a=1.
因此原方程组的解是
a=1,
b=﹣3.
3m+2n=8, ①
6m-5n=﹣47; ②
(3)
2x-4y=34, ①
5x+2y=31; ②
(4)
③-②,得
9n=63,
解得
n=7.
把n=7代入①式,得
3m+2×7=8,
解得
m=﹣2.
因此原方程组的解是
m=﹣2,
n=7.
解:①×2,得
6m+4n=16, ③
③+②,得
12x=96,
解得
x=8.
把x=8代入①式,得
2×8-4y=34,
解得
因此原方程组的解是
解:②×2,得
10x+4y=62, ③
y=﹣ .
x=8,
y=﹣ .
巩固练习
[选自教材P10 练习]
2.解下列二元一次方程组:
2(x+2y)-5y=﹣1, ①
3(x-y)+y=2; ②
(1)
, ①
; ②
(2)
③-②,得
x=﹣4,
把x=﹣4代入③式,得
2×(﹣4)-y=34,
解得
因此原方程组的解是
①×2,得
2x-y=﹣2, ③
y=﹣7.
x=﹣4,
y=﹣7.
解:化简得
2x-y=﹣1, ①
3x-2y=2; ②
解:①+②,得
y=﹣9,
解得
把y=﹣9代入②式,得
解得
x=6.
因此原方程组的解是
x=6,
y=﹣9.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
m+2n+5=0, ①
7m-2n-13=0; ②
(3)
2x+5y=0, ①
x+3y=1; ②
(4)
解:①+②,得
m=1,
解得
把m=1代入①式,得
解得
n=﹣3.
因此原方程组的解是
m=1,
n=﹣3.
m+7m+5-13=0,
1+2n+5=0,
③-①,得
y=2,
把y=2代入③式,得
2x+6×2=2,
解得
因此原方程组的解是
解:②×2,得
2x+6y=2, ③
x=﹣5.
x=﹣5,
y=2.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
2x-y=3, ①
4x+3y=﹣13; ②
(5)
1.5p-2q=﹣1, ①
﹣4.5p+7q=8; ②
(6)
③-②,得
解得
因此原方程组的解是
解:①×2,得
4x-2y=6, ③
﹣2y-3y=6-(﹣13),
解得
y=﹣ ,
把y=﹣ 代入①式,得
2x-(﹣ )=3,
x=﹣ .
x=﹣ ,
y= ﹣ .
③+②,得
q=5,
把q=5代入①式,得
1.5p-2×5=2,
解得
因此原方程组的解是
解:①×3,得
4.5p-6q=﹣3, ③
p=6.
p=6,
q=5.
[选自教材P13 习题1.2 A组 第2题 ]
巩固练习
课堂小结
代入消元法
加减消元法
解一元一次方程
二元一次方
程组的解法
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
