13.2.4三角形全等的判定——角边角 课件
文档属性
| 名称 | 13.2.4三角形全等的判定——角边角 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 165.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-01 18:18:38 | ||
图片预览



文档简介
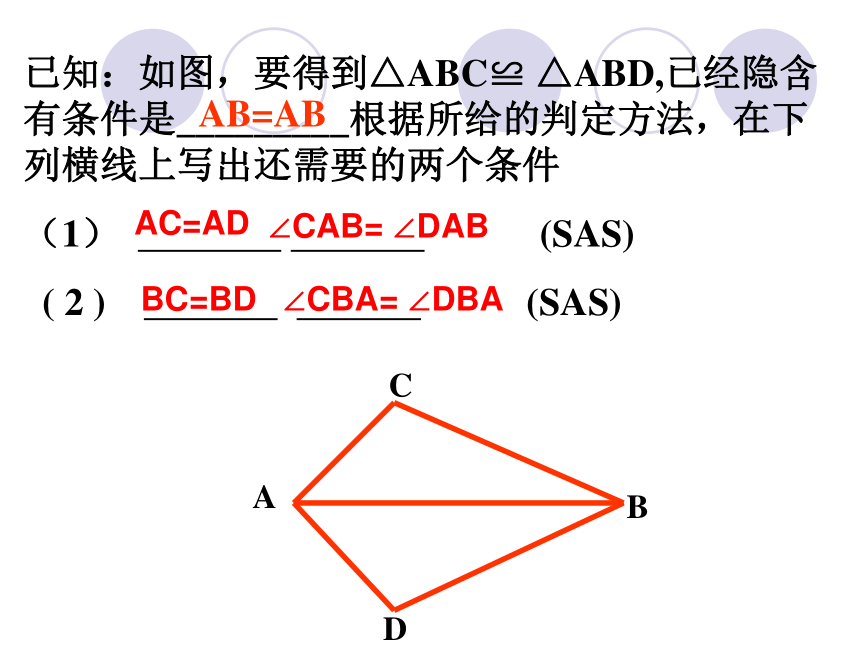
课件16张PPT。 全等三角形的判定 角边角已知:如图,要得到△ABC≌ △ABD,已经隐含有条件是_________根据所给的判定方法,在下列横线上写出还需要的两个条件
(1) (SAS)
( 2 ) (SAS)AB=ABAC=AD∠CAB= ∠DABBC=BD∠CBA= ∠DBA 当两个三角形的两条边及其夹角分别对应相等时,
两个三角形一定全等.(SAS)而当两个三角形的两条边及其中一边的对角分别对应
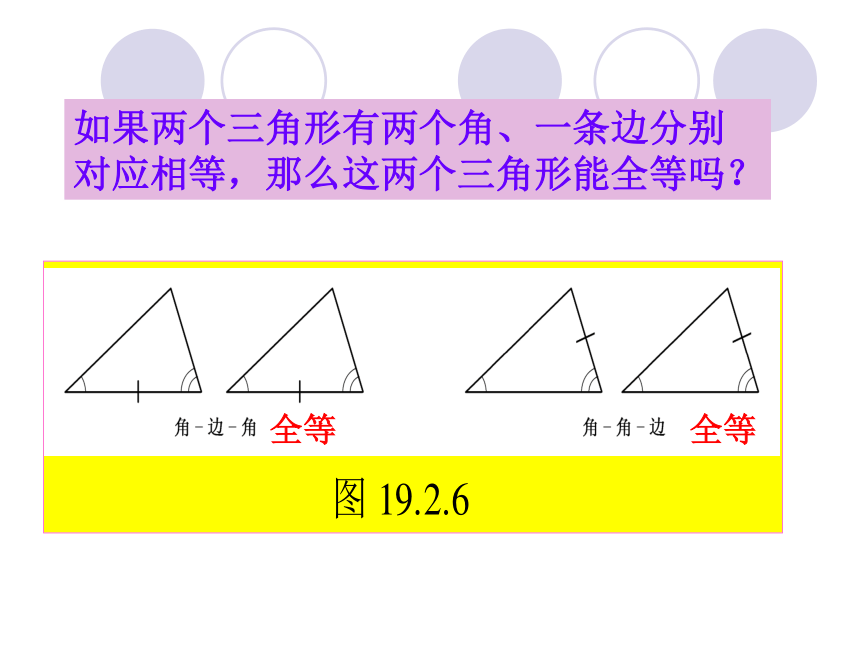
相等时,两个三角形未必一定全等.(SSA)两角一边呢如果两个三角形有两个角、一条边分别
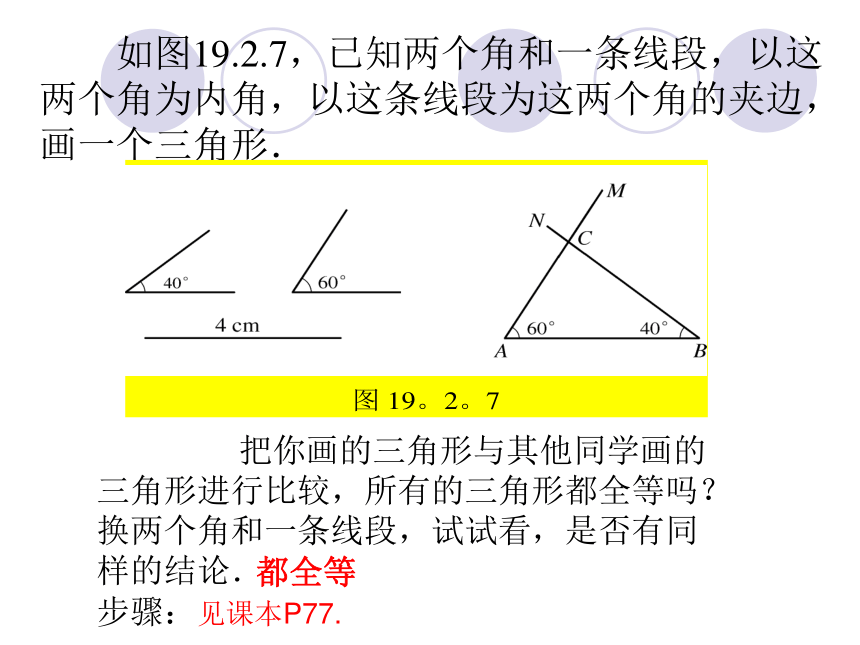
对应相等,那么这两个三角形能全等吗?全等全等 如图19.2.7,已知两个角和一条线段,以这
两个角为内角,以这条线段为这两个角的夹边,
画一个三角形.
把你画的三角形与其他同学画的
三角形进行比较,所有的三角形都全等吗?
换两个角和一条线段,试试看,是否有同
样的结论.
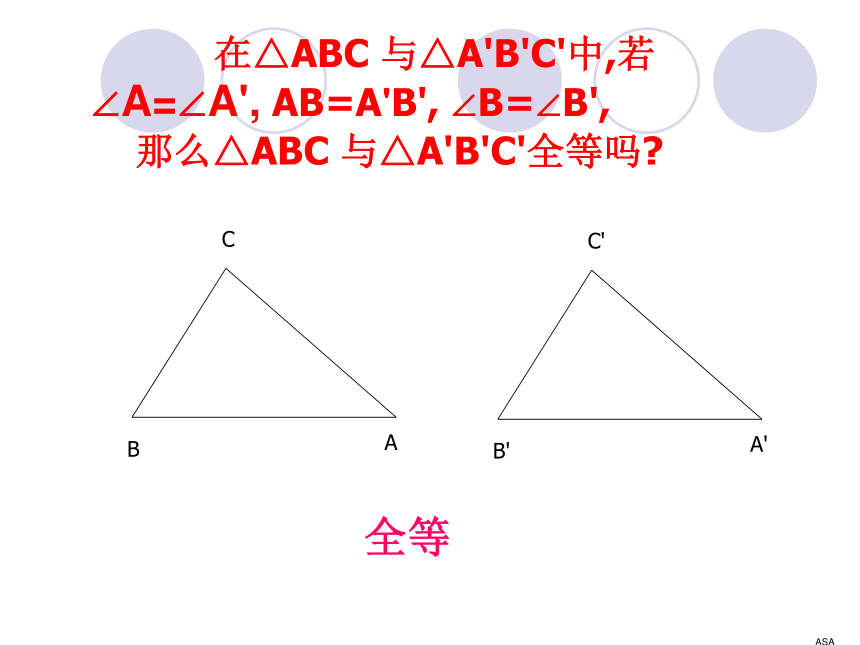
步骤:见课本P77.都全等 在△ABC 与△A'B'C'中,若
∠A=∠A', AB=A'B', ∠B=∠B',
那么△ABC 与△A'B'C'全等吗?ASA全等如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.简记为A.S.A.
(或角边角). 角边角公理在△ABC和△DEF中,△ABC≌△DEF (A.S.A.)∴用符号语言表达为:练习如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习∠AEC=∠BFDAC=BD∠A=∠B∠C=∠DAC=BD∠A=∠B如图19.2.9,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
例2 ∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明在△ABC和△DCB中,∵
∴ △ABC≌△DCB( )A.S.A.AAS?P74练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但BC不都是两个三角形两组内角的夹边,所以不全等。P74练习2、如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE
在△ ABD和△ BAE中
∠ABD=∠BAE
∵ AB=BA
∠BAD=∠ABE
∴ △ABD≌△BAE(ASA) 定理:
如果两个三角形有两个角和其中
一个角的对边分别对应相等,那么这两个三角形全等.简记为A.A.S.(或角角边).
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 如图,O是AB的中点, = , 与 全等吗?
为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)在 和 中( )例已知如图,∠1 = ∠2,∠C = ∠D
求证:AC = AD证明:在△ABC和△ABD中∠1 = ∠2
∠C = ∠D
AB = AB∴△ABC≌△ABD(AAS)
∴AC = AD(全等三角形对应边相等)谈谈本节课的收获小结请说出目前判定三角形全等的3种方法:SAS,ASA,AAS.
(1) (SAS)
( 2 ) (SAS)AB=ABAC=AD∠CAB= ∠DABBC=BD∠CBA= ∠DBA 当两个三角形的两条边及其夹角分别对应相等时,
两个三角形一定全等.(SAS)而当两个三角形的两条边及其中一边的对角分别对应
相等时,两个三角形未必一定全等.(SSA)两角一边呢如果两个三角形有两个角、一条边分别
对应相等,那么这两个三角形能全等吗?全等全等 如图19.2.7,已知两个角和一条线段,以这
两个角为内角,以这条线段为这两个角的夹边,
画一个三角形.
把你画的三角形与其他同学画的
三角形进行比较,所有的三角形都全等吗?
换两个角和一条线段,试试看,是否有同
样的结论.
步骤:见课本P77.都全等 在△ABC 与△A'B'C'中,若
∠A=∠A', AB=A'B', ∠B=∠B',
那么△ABC 与△A'B'C'全等吗?ASA全等如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.简记为A.S.A.
(或角边角). 角边角公理在△ABC和△DEF中,△ABC≌△DEF (A.S.A.)∴用符号语言表达为:练习如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上。课堂练习∠AEC=∠BFDAC=BD∠A=∠B∠C=∠DAC=BD∠A=∠B如图19.2.9,已知∠ABC=∠DCB,
∠ACB= ∠DBC,
求证: △ABC≌△DCB.
例2 ∠ABC=∠DCB,
BC=CB,
∠ACB=∠DBC,
证明在△ABC和△DCB中,∵
∴ △ABC≌△DCB( )A.S.A.AAS?P74练习 1、如图,已知∠ABC=∠D,∠ACB=∠CBD
判断图中的两个三角形是否全等,并说明理由.
不全等。因为虽然有两组内角相等,且BC=BC,但BC不都是两个三角形两组内角的夹边,所以不全等。P74练习2、如图,△ABC是等腰三角形,AD、 BE分别是
∠BAC、∠ABC的角平分线,△ABD和△BAE全等吗?
试说明理由.
全等。∵ △ABC是等腰三角形
∴ ∠ABD=∠BAE
∵ AD、 BE分别是
∠BAC、∠ABC的角平分线
∴ ∠BAD=∠ABE
在△ ABD和△ BAE中
∠ABD=∠BAE
∵ AB=BA
∠BAD=∠ABE
∴ △ABD≌△BAE(ASA) 定理:
如果两个三角形有两个角和其中
一个角的对边分别对应相等,那么这两个三角形全等.简记为A.A.S.(或角角边).
1.两个直角三角形中,斜边和一锐角对应相等,这两个直角
三角形全等吗?为什么?2.两个直角三角形中,有一条直角边和一锐角对应相等,这
两个直角三角形全等吗?为什么?答:全等,根据AAS答:全等,根据AAS 如图,O是AB的中点, = , 与 全等吗?
为什么?两角和夹边对应相等(已知)(中点的定义)(对顶角相等)在 和 中( )例已知如图,∠1 = ∠2,∠C = ∠D
求证:AC = AD证明:在△ABC和△ABD中∠1 = ∠2
∠C = ∠D
AB = AB∴△ABC≌△ABD(AAS)
∴AC = AD(全等三角形对应边相等)谈谈本节课的收获小结请说出目前判定三角形全等的3种方法:SAS,ASA,AAS.
