2023-2024学年内蒙古呼和浩特市铁路局呼和浩特职工子弟一中高一(上)期末数学模拟试卷(含解析)
文档属性
| 名称 | 2023-2024学年内蒙古呼和浩特市铁路局呼和浩特职工子弟一中高一(上)期末数学模拟试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-01-20 00:00:00 | ||
图片预览




文档简介
2023-2024学年内蒙古呼和浩特市铁路局呼和浩特职工子弟一中高一(上)期末数学模拟试卷
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)设集合M={x|x=2n,n∈Z},N={x|x=2n+1,n∈Z},P={x|x=4n,n∈Z},则( )
A.M=P B.P≠M C.N∩P≠ D.M∩N≠
2.(5分)若,那么等于( )
A.1 B. C. D.
3.(5分)若,则a,b,c的大小关系为( )
A.c>a>b B.b>a>c C.a>b>c D.b>c>a
4.(5分)下列函数中,既是偶函数,又在(0,+∞)上是增函数的是( )
A. B.y=|lnx| C.y=ex D.
5.(5分)把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是( )
A.cm2 B.4cm2 C.3cm2 D.2cm2
6.(5分)已知函数,若实数x0是方程的解,且f(x)=0,0<x1<x0,则f(x1)的值为( )
A.恒为正值 B.等于0 C.恒为负值 D.不大于0
7.(5分)某射击运动员连续射击10次,命中环数如表:
命中球数 7 8 9 10
频数 2 3 4 1
则这组数据的中位数和众数分别为( )
A.4,4 B.3.5,4 C.8.5,9 D.9,9
8.(5分)如果ab=﹣1,那么的取值范围是( )
A.(﹣∞,﹣2)∪(2,+∞) B.(﹣∞,﹣2]∪[2,+∞)
C.(﹣2,2) D.[﹣2,2]
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)设0<b<a<1,则下列不等式不成立的是( )
A.ab<b2<1 B. C. D.a2<ab<1
(多选)10.(5分)下列四个命题中正确的是( )
A.若事件A,B是互斥事件,则A,B是对立事件
B.若事件A,B是对立事件,则A,B是互斥事件
C.若事件A是必然事件,则P(A)=1
D.若事件A,B是互斥事件,则P(A∪B)=1
(多选)11.(5分)已知函数f(x)=loga(x﹣1)+2(a>0,且a≠1)的图象过定点(s,t),正数m,n满足m+n=s+t,则( )
A.m+n=4 B.m2+n2≥8 C.mn≥4 D.
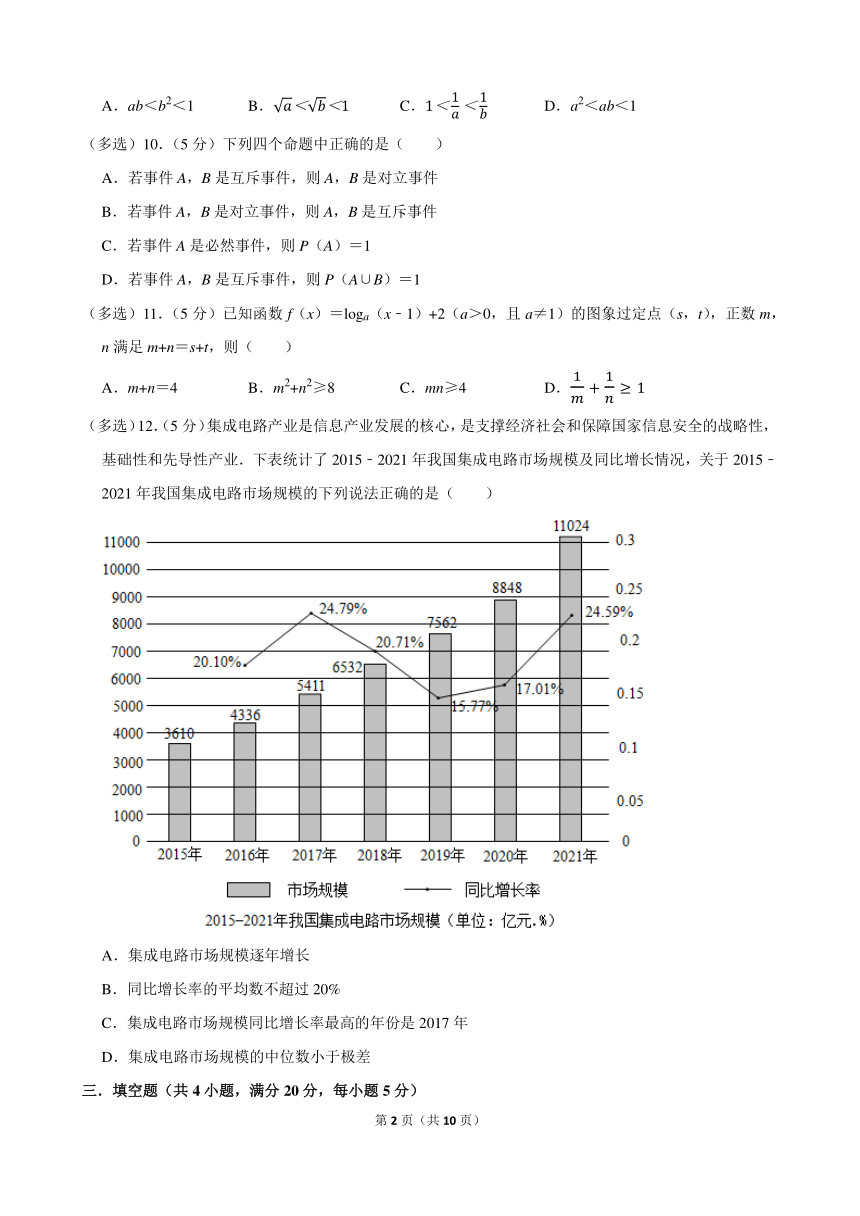
(多选)12.(5分)集成电路产业是信息产业发展的核心,是支撑经济社会和保障国家信息安全的战略性,基础性和先导性产业.下表统计了2015﹣2021年我国集成电路市场规模及同比增长情况,关于2015﹣2021年我国集成电路市场规模的下列说法正确的是( )
A.集成电路市场规模逐年增长
B.同比增长率的平均数不超过20%
C.集成电路市场规模同比增长率最高的年份是2017年
D.集成电路市场规模的中位数小于极差
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)用计算机或计算器模拟试验的方法称为 .
14.(5分)已知正实数x,y满足x+y+z=3,xy+yz+zx=2,则实数z的取值范围是 .
15.(5分)5G指的是第五代移动通信技术,比第四代移动通信技术的数据传输速率快数百倍,某公司在研发5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,已知甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.则该公司攻克这项技术难题的概率为 .
16.(5分)已知函数f(x),且f(x)在R上递减,则实数a的取值范围 .
四.解答题(共6小题,满分70分)
17.(10分)解下列不等式.
(1)6﹣2x≤x2﹣3x<18;
(2);
(3)x2﹣3|x|+2>0.
18.(12分)(1)()680.25﹣(﹣2019)0;
(2)2log32﹣log3.
19.(12分)某地举办了一次地区性的中国象棋比赛,小明作为选手参加.除小明外的其他参赛选手中,一、二、三类棋手的人数之比为5:7:8,小明与一、二、三类棋手比赛获胜的概率分别是0.6、0.5、0.4.
(1)从参赛选手中随机抽取一位棋手与小明比赛,求小明获胜的概率;
(2)如果小明获胜,求与小明比赛的棋手分别为一、二、三类棋手的概率.
20.(12分)已知2<a<3,﹣2<b<﹣1,求ab,的取值范围.
21.(12分)世界各国越来越关注环境保护问题,某检测点连续100天监视空气质量指数(AQI),将这100天的AQI数据分为五组,各组对应的区间为[0,50),[50,100),[100,150),[150,200),[200,250].并绘制出如图所示的不完整的频率分布直方图.
(1)请将频率分布直方图补充完整;
(2)已知空气质量指数AQI在[0,50)内的空气质量等级为优,在[50,100)内的空气质量等级为良,分别求这100天中空气质量等级为优与空气质量等级为良的天数;
(3)在(2)的条件下,在空气质量等级为优和良的天数中,先按分层抽样的方法已经选定了6天,然后再从这6天中任取两天,求这两天的空气质量等级相同的概率.
22.(12分)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在函数的图象(弹道曲线)上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)确定k的值使炮弹恰好击中坐标为(2,3)的目标P;若目标P成功躲避炮弹射击,该枚炮弹的射程是多少?
(2)求炮的射程关于k的函数解析式x=f(k),并求炮的最大射程;
(3)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
2023-2024学年内蒙古呼和浩特市铁路局呼和浩特职工子弟一中高一(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:∵集合M={x|x=2n,n∈Z},
N={x|x=2n+1,n∈Z},
P={x|x=4n,n∈Z},
∴M≠P,N∩P= ,M∩N= ,
故选:B.
2.【解答】解:∵,
∴当x=﹣2时,,
故选:C.
3.【解答】解:∵,,
∴b>a>c.
故选:B.
4.【解答】解:对于A中,函数,则f(﹣x)=f(x),
所以函数f(x)为偶函数,且f(x)=x在区间(0,+∞)上为单调递增函数,符合题意;
对于B中,函数f(x)=|lnx|的定义域为(0,+∞),所以函数f(x)为非奇非偶函数,不符合题意;
对于C中,函数f(x)=ex,根据指数函数的性质,可得函数f(x)为非奇非偶函数,不符合题意;
对于D中,函数的定义域为(﹣∞,0)∪(0,+∞),关于原点对称,
且满足f(﹣x)=f(x),所以函数f(x)为偶函数,
当x∈(0,+∞)时,可得为单调递减函数,不符合题意.
故选:A.
5.【解答】解:设两段长分别为xcm,(12﹣x)cm,
则这两个正三角形面积之和 S()2()2
(x2﹣12x+72)[(x﹣6)2+36]≥2,
故选:D.
6.【解答】解:分别作出函数是减函数,h(x)=log2x的图象,如图.
在(0,+∞) 是减函数,h(x)=log2x是增函数,
所以函数,在(0,+∞)上是减函数,所以f(x1)>f(x0)=0,
故选:A.
7.【解答】解:由已知该运动员射中7环2次,8环3次,9环4次,10环1次,
射中9环的次数最多,所以命中环数的众数为9,
将所有数据按从小到大排列可得7,7,8,8,8,9,9,9,9,10,
所以命中环数的中位数为.
故选:C.
8.【解答】解:∵ab=﹣1∴b
∴a﹣b=a
要使上式有意义a≠±1
当a>0时,a22,等号取不到;
当a<0时,a(﹣a)≤﹣22,等号取不到;
综上所述w的范围是(﹣∞,﹣2)∪(2,+∞)
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:A:因为0<b<a<1,则ab>b2,故A错误,
B:因为0<b<a<1,则,故B错误,
C:因为0<b<a<1,则1,故C正确,
D:因为0<b<a<1,则a2>ab,故D错误,
故选:ABD.
10.【解答】解:根据题意,依次分析选项:
对于A,互斥事件不一定是对立事件,A错误;
对于B,对立事件一定互斥,B正确;
对于C,若事件A是必然事件,则P(A)=1,C正确;
对于D,当事件A,B是对立事件时,P(A∪B)=1,D错误;
故选:BC.
11.【解答】解:由题意得,函数f(x)的图象过定点(2,2),s=t=2,所以m+n=4,所以A正确;
由重要不等式m2+n2≥2mn可得2(m2+n2)≥(m+n)2=16,
故m2+n2≥8,当且仅当m=n=2时取等号,所以B正确;
由基本不等式可得,,当且仅当,m=n=2时取等号,故C错误;
又,
当且仅当,即m=n=2时取等号,所以D正确.
故选:ABD.
12.【解答】解:对于A,由图可知,集成电路市场规模逐年增长,故A正确;
对于B,同比增长率的平均数为:
(20.10%+24.79%+20.71%+15.77%+17.01%+24.59%)=20.495%>20%,故B不正确;
对于C,集成电路市场规模同比增长率最高的年份是2017年,为24.79%,故C正确;
对于D,集成电路市场规模的中位数为:6532,集成电路市场规模的极差为:11024﹣3610=7414>6532,故D正确.
故选:ACD.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:用计算机或计算器模拟试验的方法称为随机模拟法或梦特卡洛方法.
故答案为:随机模拟法或梦特卡洛方法.
14.【解答】解:由 已知可得y=3﹣(x+z),
所以,xy+yz+zx=x(3﹣x﹣z)+(3﹣x﹣z)z+xz=2,
即x2+(z﹣3)x+z2﹣3z+2=0,
由题意可得,Δ=(z﹣3)2﹣4(z2﹣3z+2)≥0,
解可得,,
又即3>z>2或z<1,
综上可得,,
故答案为:{z|}.
15.【解答】解:某公司在研发5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,
甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.
设事件A表示”甲部门攻克该技术难题“,事件B表示“乙部门攻克该技术难题”,
则P(A)=0.6,P(B)=0.5,
该公司攻克这项技术难题的概率为:
P=1﹣P()=1﹣(1﹣0.6)(1﹣0.5)=0.8.
故答案为:0.8.
16.【解答】解:∵函数f(x)在R上单调递减,
∴,求得2≤a≤3,
故答案为:[2,3].
四.解答题(共6小题,满分70分)
17.【解答】解:(1)原不等式等价于,即,
解得,
∴﹣3<x≤﹣2或3≤x<6,
即不等式的解集为(﹣3,﹣2]∪[3,6).
(2)原不等式等价于,即,
∴,
等价于(2x﹣3)(3x﹣1)≤0且3x﹣1≠0,
解得,
所以不等式的解集为(,].
(3)当x≥0时,不等式化为x2﹣3x+2>0,
解得x<1或x>2,
∴0≤x<1或x>2,
当x<0时,不等式化为x2+3x+2>0,
解得x<﹣2或x>﹣1,
∴x<﹣2或﹣1<x<0,
综上所述,不等式的解集为(﹣∞,﹣2)∪(﹣1,1)∪(2,+∞).
18.【解答】解:(1)原式1=22×33﹣2﹣1=105;
(2)原式.
19.【解答】解:(1)小明与其他参赛选手中,一、二、三类棋手相遇的概率分别为0.25,0.35,0.4,
从参赛选手中随机抽取一位棋手与小明比赛,小明获胜的概率为0.25×0.6+0.35×0.5+0.4×0.4=0.485.
(2)小明获胜,与小明比赛的棋手为一类棋手的概率为,
小明获胜,与小明比赛的棋手为二类棋手的概率为,
小明获胜,与小明比赛的棋手为三类棋手的概率为.
20.【解答】解:①∵﹣2<b<﹣1,∴1<﹣b<2,又2<a<3,∴2<﹣ab<6,∴﹣6<ab<﹣2;
②∵2<a<3,﹣2<b<﹣1,∴,1<b2<4,∴.
21.【解答】解:(1)因为AQI在[100,150)内的频率为1﹣50×(0.004+0.008+0.002+0.001)=0.25,
所以AQI在[100,150)内的,
故频率分布直方图补充完整如图所示.
(2)这100天中空气质量等级为优的天数为50×0.004×100=20,
空气质量等级为良的天数为50×0.008×100=40.
(3)由(2)可知,选定的6天中有2天空气质量等级为优,有4天为良分别记为A1,A2和B1,B2,B3,B4,
记事件“从这6天中任取两天,这两天的空气质量等级相同”为M,
则事件M包含的基本事件有(A1,A2),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),
共有7个基本事件,
而从6天中任取两天包含的基本事件有:
(A1,A2),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),(A1,B1),
(A2,B1),(A1,B2),(A2,B2),(A1,B3),(A2,B3),(A1,B4),(A2,B4),共有15个基本事件,
∴从这6天中任取两天,这两天的空气质量等级相同的概率.
22.【解答】解:(1)由题意,点P(2,3)在函数y=kx(1+k2)x2(k>0)的图象上,
∴2k(1+k2) 22=3,解得k=2或k=8,
当k=2时,弹道曲线为y=2x(x>0),令y=0,得x=2,
当k=8时,弹道曲线为y=8xx2(x>0),令y=0,得x,
∴当k=2或8时,炮弹恰好击中坐标为(2,3)的目标P,
此时炮弹未能击中目标的射程分别是2千数或千米.
(2)在y=kx(1+k2)x2(k>0)中,令y=0,得kx0,
由实际意义和题设条件知x>0,k>0,∴x=f(k),k>0,
∴x10,
当且仅当k=1时,取等号,∴炮的最大射程是10千米.
(3)∵a>0,∴炮弹可以击中目标等价于存在k>0,使ka(1+k2)a2=3.2成立,
即关于k的方程a2k2﹣20ak+a2+64=0有正根,
由Δ=(﹣20a)2﹣4a2(a2+64)≥0,得a≤6,
此时,k0,
当a不超过6千米时,炮弹可以击中目标.
第1页(共1页)
一.选择题(共8小题,满分40分,每小题5分)
1.(5分)设集合M={x|x=2n,n∈Z},N={x|x=2n+1,n∈Z},P={x|x=4n,n∈Z},则( )
A.M=P B.P≠M C.N∩P≠ D.M∩N≠
2.(5分)若,那么等于( )
A.1 B. C. D.
3.(5分)若,则a,b,c的大小关系为( )
A.c>a>b B.b>a>c C.a>b>c D.b>c>a
4.(5分)下列函数中,既是偶函数,又在(0,+∞)上是增函数的是( )
A. B.y=|lnx| C.y=ex D.
5.(5分)把长为12cm的细铁丝截成两段,各自围成一个正三角形,那么这两个正三角形面积之和的最小值是( )
A.cm2 B.4cm2 C.3cm2 D.2cm2
6.(5分)已知函数,若实数x0是方程的解,且f(x)=0,0<x1<x0,则f(x1)的值为( )
A.恒为正值 B.等于0 C.恒为负值 D.不大于0
7.(5分)某射击运动员连续射击10次,命中环数如表:
命中球数 7 8 9 10
频数 2 3 4 1
则这组数据的中位数和众数分别为( )
A.4,4 B.3.5,4 C.8.5,9 D.9,9
8.(5分)如果ab=﹣1,那么的取值范围是( )
A.(﹣∞,﹣2)∪(2,+∞) B.(﹣∞,﹣2]∪[2,+∞)
C.(﹣2,2) D.[﹣2,2]
二.多选题(共4小题,满分20分,每小题5分)
(多选)9.(5分)设0<b<a<1,则下列不等式不成立的是( )
A.ab<b2<1 B. C. D.a2<ab<1
(多选)10.(5分)下列四个命题中正确的是( )
A.若事件A,B是互斥事件,则A,B是对立事件
B.若事件A,B是对立事件,则A,B是互斥事件
C.若事件A是必然事件,则P(A)=1
D.若事件A,B是互斥事件,则P(A∪B)=1
(多选)11.(5分)已知函数f(x)=loga(x﹣1)+2(a>0,且a≠1)的图象过定点(s,t),正数m,n满足m+n=s+t,则( )
A.m+n=4 B.m2+n2≥8 C.mn≥4 D.
(多选)12.(5分)集成电路产业是信息产业发展的核心,是支撑经济社会和保障国家信息安全的战略性,基础性和先导性产业.下表统计了2015﹣2021年我国集成电路市场规模及同比增长情况,关于2015﹣2021年我国集成电路市场规模的下列说法正确的是( )
A.集成电路市场规模逐年增长
B.同比增长率的平均数不超过20%
C.集成电路市场规模同比增长率最高的年份是2017年
D.集成电路市场规模的中位数小于极差
三.填空题(共4小题,满分20分,每小题5分)
13.(5分)用计算机或计算器模拟试验的方法称为 .
14.(5分)已知正实数x,y满足x+y+z=3,xy+yz+zx=2,则实数z的取值范围是 .
15.(5分)5G指的是第五代移动通信技术,比第四代移动通信技术的数据传输速率快数百倍,某公司在研发5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,已知甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.则该公司攻克这项技术难题的概率为 .
16.(5分)已知函数f(x),且f(x)在R上递减,则实数a的取值范围 .
四.解答题(共6小题,满分70分)
17.(10分)解下列不等式.
(1)6﹣2x≤x2﹣3x<18;
(2);
(3)x2﹣3|x|+2>0.
18.(12分)(1)()680.25﹣(﹣2019)0;
(2)2log32﹣log3.
19.(12分)某地举办了一次地区性的中国象棋比赛,小明作为选手参加.除小明外的其他参赛选手中,一、二、三类棋手的人数之比为5:7:8,小明与一、二、三类棋手比赛获胜的概率分别是0.6、0.5、0.4.
(1)从参赛选手中随机抽取一位棋手与小明比赛,求小明获胜的概率;
(2)如果小明获胜,求与小明比赛的棋手分别为一、二、三类棋手的概率.
20.(12分)已知2<a<3,﹣2<b<﹣1,求ab,的取值范围.
21.(12分)世界各国越来越关注环境保护问题,某检测点连续100天监视空气质量指数(AQI),将这100天的AQI数据分为五组,各组对应的区间为[0,50),[50,100),[100,150),[150,200),[200,250].并绘制出如图所示的不完整的频率分布直方图.
(1)请将频率分布直方图补充完整;
(2)已知空气质量指数AQI在[0,50)内的空气质量等级为优,在[50,100)内的空气质量等级为良,分别求这100天中空气质量等级为优与空气质量等级为良的天数;
(3)在(2)的条件下,在空气质量等级为优和良的天数中,先按分层抽样的方法已经选定了6天,然后再从这6天中任取两天,求这两天的空气质量等级相同的概率.
22.(12分)如图,建立平面直角坐标系xOy,x轴在地平面上,y轴垂直于地平面,单位长度为1千米.某炮位于坐标原点.已知炮弹发射后的轨迹在函数的图象(弹道曲线)上,其中k与发射方向有关.炮的射程是指炮弹落地点的横坐标.
(1)确定k的值使炮弹恰好击中坐标为(2,3)的目标P;若目标P成功躲避炮弹射击,该枚炮弹的射程是多少?
(2)求炮的射程关于k的函数解析式x=f(k),并求炮的最大射程;
(3)设在第一象限有一飞行物(忽略其大小),其飞行高度为3.2千米,试问它的横坐标a不超过多少时,炮弹可以击中它?请说明理由.
2023-2024学年内蒙古呼和浩特市铁路局呼和浩特职工子弟一中高一(上)期末数学模拟试卷
参考答案与试题解析
一.选择题(共8小题,满分40分,每小题5分)
1.【解答】解:∵集合M={x|x=2n,n∈Z},
N={x|x=2n+1,n∈Z},
P={x|x=4n,n∈Z},
∴M≠P,N∩P= ,M∩N= ,
故选:B.
2.【解答】解:∵,
∴当x=﹣2时,,
故选:C.
3.【解答】解:∵,,
∴b>a>c.
故选:B.
4.【解答】解:对于A中,函数,则f(﹣x)=f(x),
所以函数f(x)为偶函数,且f(x)=x在区间(0,+∞)上为单调递增函数,符合题意;
对于B中,函数f(x)=|lnx|的定义域为(0,+∞),所以函数f(x)为非奇非偶函数,不符合题意;
对于C中,函数f(x)=ex,根据指数函数的性质,可得函数f(x)为非奇非偶函数,不符合题意;
对于D中,函数的定义域为(﹣∞,0)∪(0,+∞),关于原点对称,
且满足f(﹣x)=f(x),所以函数f(x)为偶函数,
当x∈(0,+∞)时,可得为单调递减函数,不符合题意.
故选:A.
5.【解答】解:设两段长分别为xcm,(12﹣x)cm,
则这两个正三角形面积之和 S()2()2
(x2﹣12x+72)[(x﹣6)2+36]≥2,
故选:D.
6.【解答】解:分别作出函数是减函数,h(x)=log2x的图象,如图.
在(0,+∞) 是减函数,h(x)=log2x是增函数,
所以函数,在(0,+∞)上是减函数,所以f(x1)>f(x0)=0,
故选:A.
7.【解答】解:由已知该运动员射中7环2次,8环3次,9环4次,10环1次,
射中9环的次数最多,所以命中环数的众数为9,
将所有数据按从小到大排列可得7,7,8,8,8,9,9,9,9,10,
所以命中环数的中位数为.
故选:C.
8.【解答】解:∵ab=﹣1∴b
∴a﹣b=a
要使上式有意义a≠±1
当a>0时,a22,等号取不到;
当a<0时,a(﹣a)≤﹣22,等号取不到;
综上所述w的范围是(﹣∞,﹣2)∪(2,+∞)
故选:A.
二.多选题(共4小题,满分20分,每小题5分)
9.【解答】解:A:因为0<b<a<1,则ab>b2,故A错误,
B:因为0<b<a<1,则,故B错误,
C:因为0<b<a<1,则1,故C正确,
D:因为0<b<a<1,则a2>ab,故D错误,
故选:ABD.
10.【解答】解:根据题意,依次分析选项:
对于A,互斥事件不一定是对立事件,A错误;
对于B,对立事件一定互斥,B正确;
对于C,若事件A是必然事件,则P(A)=1,C正确;
对于D,当事件A,B是对立事件时,P(A∪B)=1,D错误;
故选:BC.
11.【解答】解:由题意得,函数f(x)的图象过定点(2,2),s=t=2,所以m+n=4,所以A正确;
由重要不等式m2+n2≥2mn可得2(m2+n2)≥(m+n)2=16,
故m2+n2≥8,当且仅当m=n=2时取等号,所以B正确;
由基本不等式可得,,当且仅当,m=n=2时取等号,故C错误;
又,
当且仅当,即m=n=2时取等号,所以D正确.
故选:ABD.
12.【解答】解:对于A,由图可知,集成电路市场规模逐年增长,故A正确;
对于B,同比增长率的平均数为:
(20.10%+24.79%+20.71%+15.77%+17.01%+24.59%)=20.495%>20%,故B不正确;
对于C,集成电路市场规模同比增长率最高的年份是2017年,为24.79%,故C正确;
对于D,集成电路市场规模的中位数为:6532,集成电路市场规模的极差为:11024﹣3610=7414>6532,故D正确.
故选:ACD.
三.填空题(共4小题,满分20分,每小题5分)
13.【解答】解:用计算机或计算器模拟试验的方法称为随机模拟法或梦特卡洛方法.
故答案为:随机模拟法或梦特卡洛方法.
14.【解答】解:由 已知可得y=3﹣(x+z),
所以,xy+yz+zx=x(3﹣x﹣z)+(3﹣x﹣z)z+xz=2,
即x2+(z﹣3)x+z2﹣3z+2=0,
由题意可得,Δ=(z﹣3)2﹣4(z2﹣3z+2)≥0,
解可得,,
又即3>z>2或z<1,
综上可得,,
故答案为:{z|}.
15.【解答】解:某公司在研发5G项目时遇到一项技术难题,由甲、乙两个部门分别独立攻关,
甲部门攻克该技术难题的概率为0.6,乙部门攻克该技术难题的概率为0.5.
设事件A表示”甲部门攻克该技术难题“,事件B表示“乙部门攻克该技术难题”,
则P(A)=0.6,P(B)=0.5,
该公司攻克这项技术难题的概率为:
P=1﹣P()=1﹣(1﹣0.6)(1﹣0.5)=0.8.
故答案为:0.8.
16.【解答】解:∵函数f(x)在R上单调递减,
∴,求得2≤a≤3,
故答案为:[2,3].
四.解答题(共6小题,满分70分)
17.【解答】解:(1)原不等式等价于,即,
解得,
∴﹣3<x≤﹣2或3≤x<6,
即不等式的解集为(﹣3,﹣2]∪[3,6).
(2)原不等式等价于,即,
∴,
等价于(2x﹣3)(3x﹣1)≤0且3x﹣1≠0,
解得,
所以不等式的解集为(,].
(3)当x≥0时,不等式化为x2﹣3x+2>0,
解得x<1或x>2,
∴0≤x<1或x>2,
当x<0时,不等式化为x2+3x+2>0,
解得x<﹣2或x>﹣1,
∴x<﹣2或﹣1<x<0,
综上所述,不等式的解集为(﹣∞,﹣2)∪(﹣1,1)∪(2,+∞).
18.【解答】解:(1)原式1=22×33﹣2﹣1=105;
(2)原式.
19.【解答】解:(1)小明与其他参赛选手中,一、二、三类棋手相遇的概率分别为0.25,0.35,0.4,
从参赛选手中随机抽取一位棋手与小明比赛,小明获胜的概率为0.25×0.6+0.35×0.5+0.4×0.4=0.485.
(2)小明获胜,与小明比赛的棋手为一类棋手的概率为,
小明获胜,与小明比赛的棋手为二类棋手的概率为,
小明获胜,与小明比赛的棋手为三类棋手的概率为.
20.【解答】解:①∵﹣2<b<﹣1,∴1<﹣b<2,又2<a<3,∴2<﹣ab<6,∴﹣6<ab<﹣2;
②∵2<a<3,﹣2<b<﹣1,∴,1<b2<4,∴.
21.【解答】解:(1)因为AQI在[100,150)内的频率为1﹣50×(0.004+0.008+0.002+0.001)=0.25,
所以AQI在[100,150)内的,
故频率分布直方图补充完整如图所示.
(2)这100天中空气质量等级为优的天数为50×0.004×100=20,
空气质量等级为良的天数为50×0.008×100=40.
(3)由(2)可知,选定的6天中有2天空气质量等级为优,有4天为良分别记为A1,A2和B1,B2,B3,B4,
记事件“从这6天中任取两天,这两天的空气质量等级相同”为M,
则事件M包含的基本事件有(A1,A2),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),
共有7个基本事件,
而从6天中任取两天包含的基本事件有:
(A1,A2),(B1,B2),(B1,B3),(B1,B4),(B2,B3),(B2,B4),(B3,B4),(A1,B1),
(A2,B1),(A1,B2),(A2,B2),(A1,B3),(A2,B3),(A1,B4),(A2,B4),共有15个基本事件,
∴从这6天中任取两天,这两天的空气质量等级相同的概率.
22.【解答】解:(1)由题意,点P(2,3)在函数y=kx(1+k2)x2(k>0)的图象上,
∴2k(1+k2) 22=3,解得k=2或k=8,
当k=2时,弹道曲线为y=2x(x>0),令y=0,得x=2,
当k=8时,弹道曲线为y=8xx2(x>0),令y=0,得x,
∴当k=2或8时,炮弹恰好击中坐标为(2,3)的目标P,
此时炮弹未能击中目标的射程分别是2千数或千米.
(2)在y=kx(1+k2)x2(k>0)中,令y=0,得kx0,
由实际意义和题设条件知x>0,k>0,∴x=f(k),k>0,
∴x10,
当且仅当k=1时,取等号,∴炮的最大射程是10千米.
(3)∵a>0,∴炮弹可以击中目标等价于存在k>0,使ka(1+k2)a2=3.2成立,
即关于k的方程a2k2﹣20ak+a2+64=0有正根,
由Δ=(﹣20a)2﹣4a2(a2+64)≥0,得a≤6,
此时,k0,
当a不超过6千米时,炮弹可以击中目标.
第1页(共1页)
同课章节目录
