天津市梅江中学八年级数学下册18.1.1 平行四边形的性质课件1 (新人教版)
文档属性
| 名称 | 天津市梅江中学八年级数学下册18.1.1 平行四边形的性质课件1 (新人教版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-02 00:00:00 | ||
图片预览



文档简介
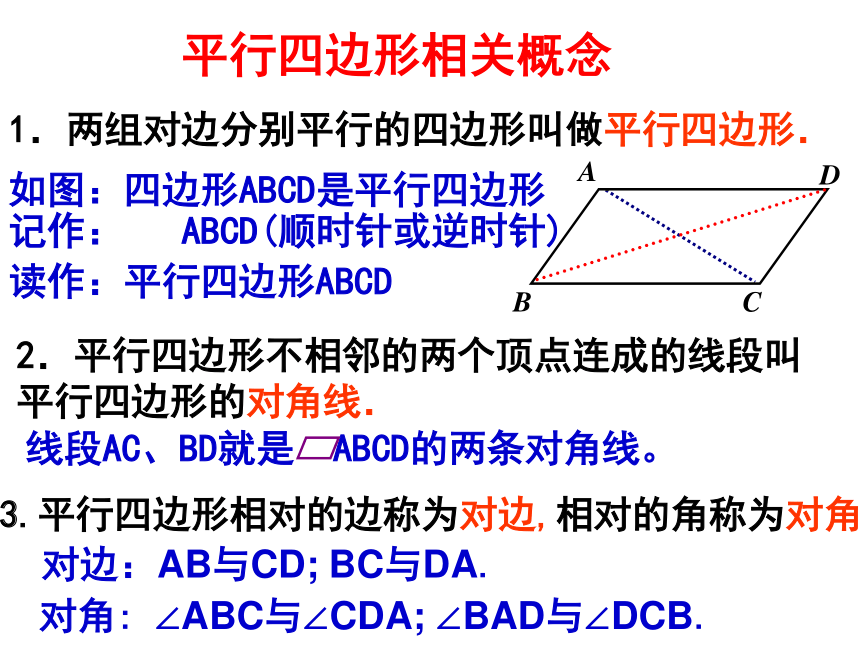
课件32张PPT。平行四边形1.两组对边分别平行的四边形叫做平行四边形.如图:四边形ABCD是平行四边形记作: ABCD(顺时针或逆时针)
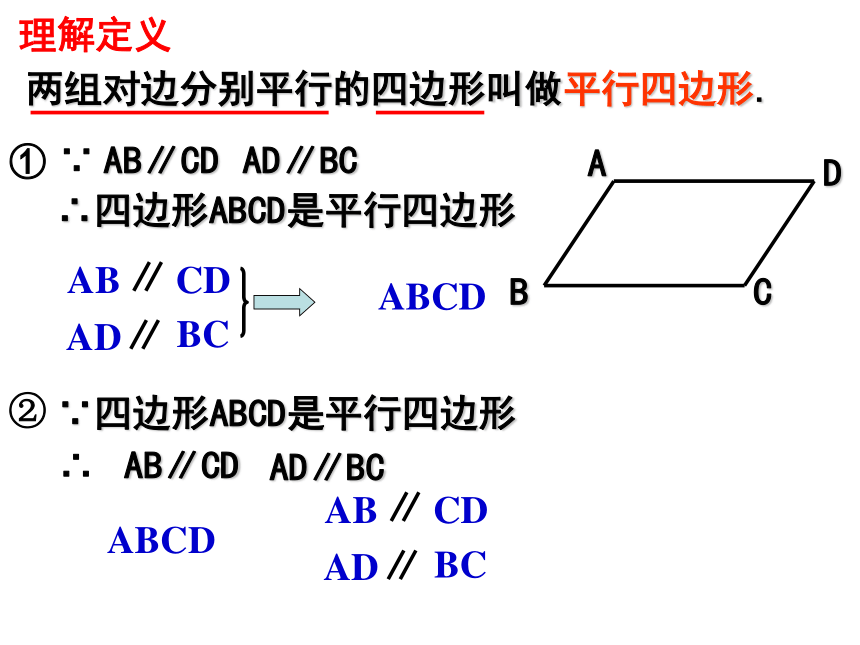
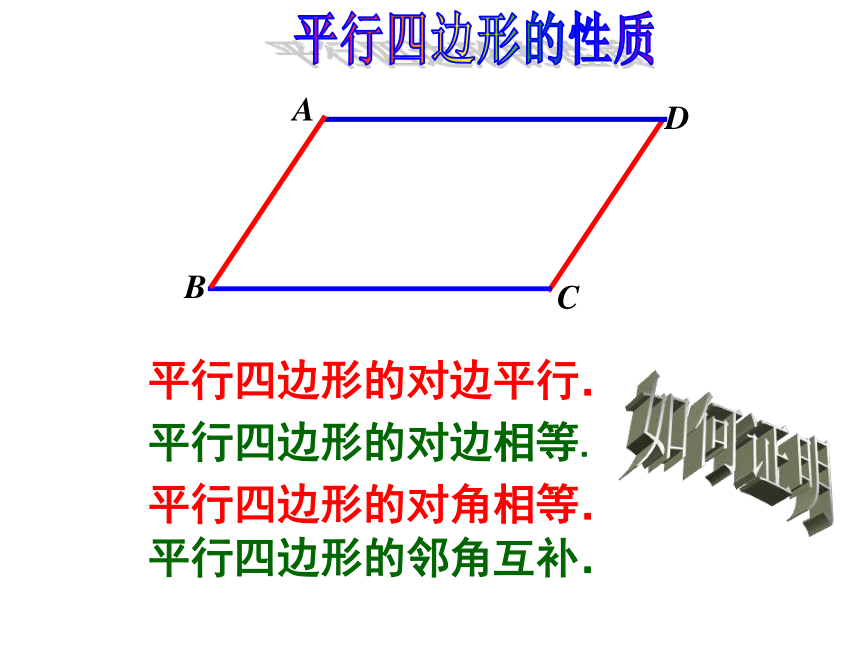
读作:平行四边形ABCD2.平行四边形不相邻的两个顶点连成的线段叫 平行四边形的对角线.3.平行四边形相对的边称为对边,相对的角称为对角平行四边形相关概念对边:AB与CD; BC与DA.对角: ∠ABC与∠CDA; ∠BAD与∠DCB.两组对边分别平行的四边形叫做平行四边形.∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形AB∥CDAD∥BC∴ 理解定义ABCD①②ABCD 平行四边形的边、角有怎样的数量关系?猜一猜平行四边形的对边平行.
平行四边形的对边相等.
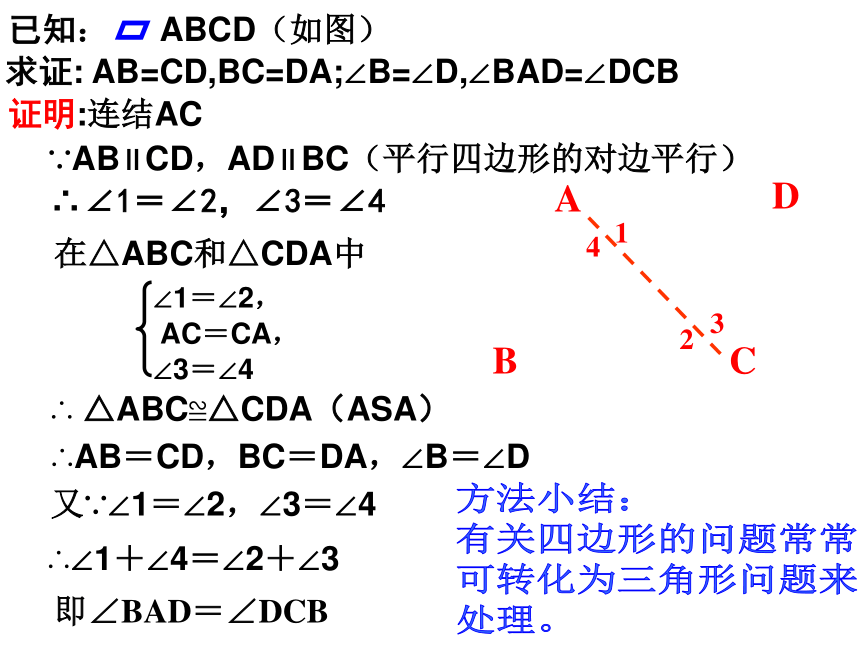
平行四边形的对角相等.平行四边形的邻角互补.ABCD平行四边形的性质如何证明即∠BAD=∠DCB证明:连结AC ∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在△ABC和△CDA中ABCD求证: AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB方法小结:
有关四边形的问题常常
可转化为三角形问题来
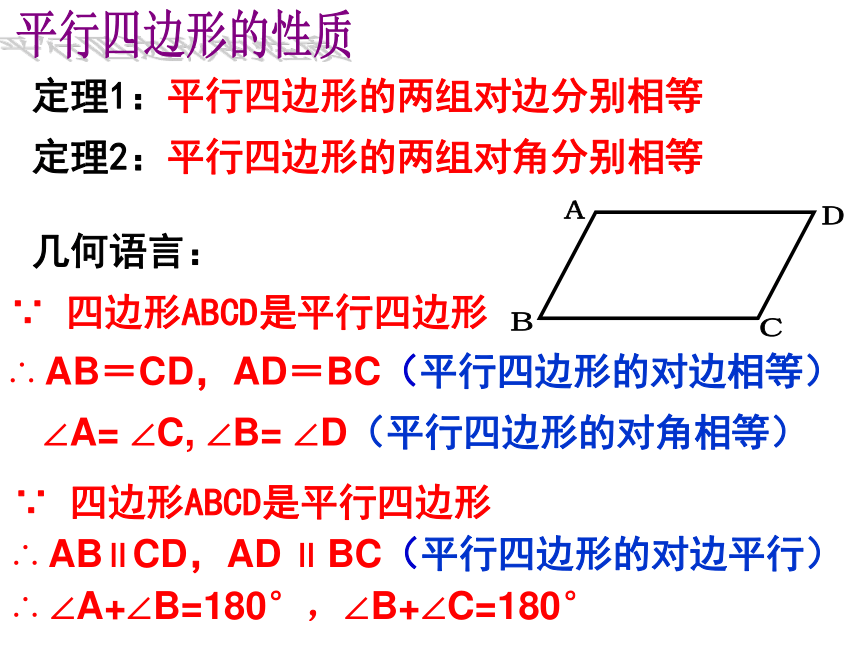
处理。平行四边形的性质几何语言:定理1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC(平行四边形的对边相等)∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 定理2:平行四边形的两组对角分别相等∴ ∠A+∠B=180°,∠B+∠C=180°∵ 四边形ABCD是平行四边形∴ AB∥CD,AD ∥ BC(平行四边形的对边平行) 1.如图:在 ABCD中,根据已知你能得到哪
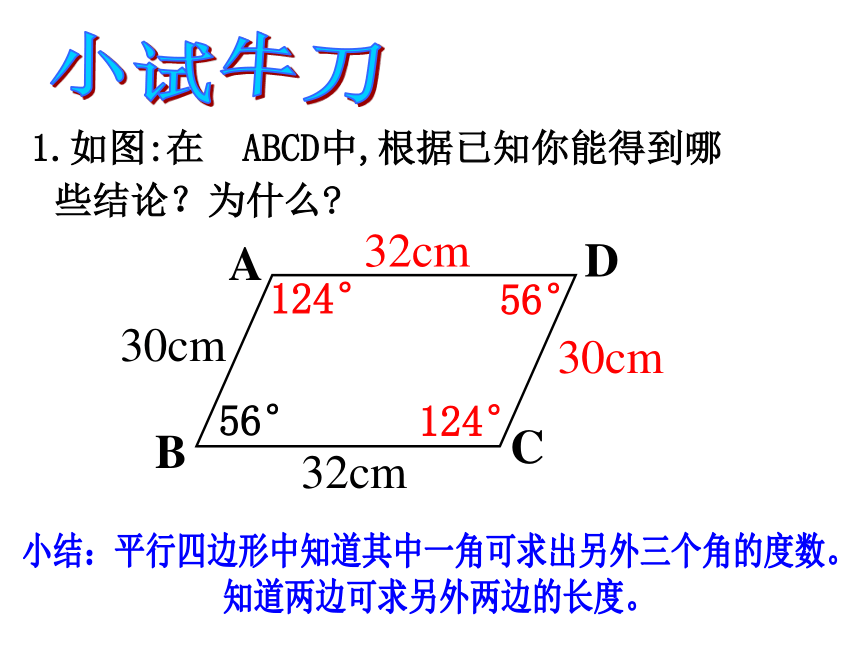
些结论?为什么?32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数。
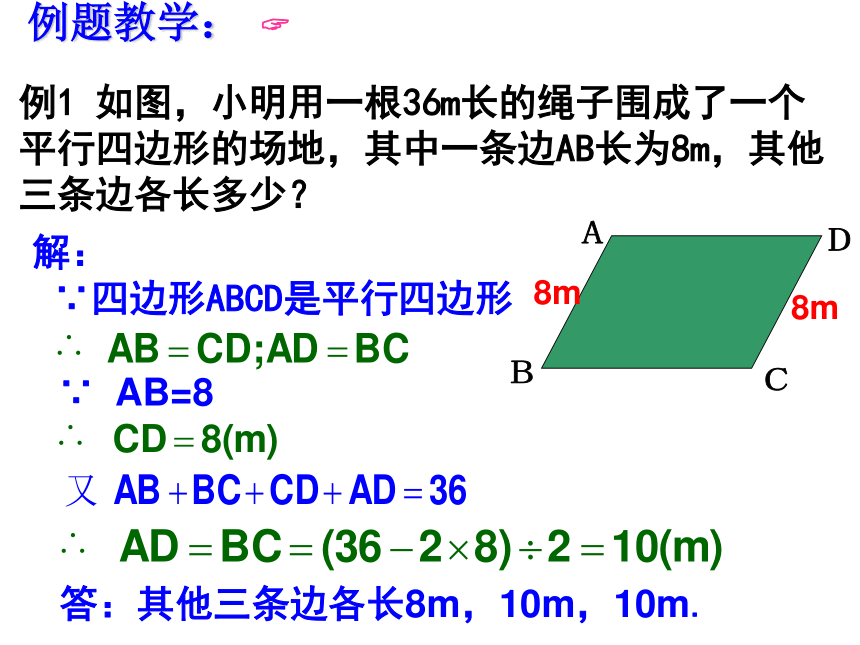
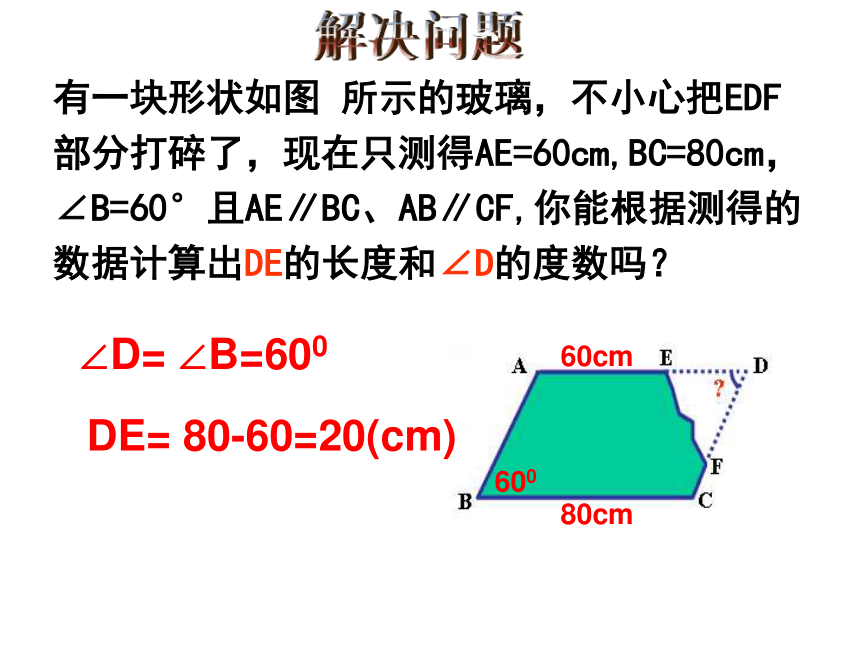
知道两边可求另外两边的长度。小试牛刀 例题教学: ? 例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵ AB=8∴∴∴答:其他三条边各长8m,10m,10m.8m8m有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?解决问题60cm80cm600∠D= ∠B=600DE= 80-60=20(cm) 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。 随堂练习: 401. 在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ; AB= ;
∠A= , ∠C= , ∠D= .30120°120°60°403060°2. 在 ABCD 中,∠ADC=120°,
∠CAD=20°,则
∠ABC= , ∠CAB= .120°40°20°120°20°20°3.如图, ABCD的周长是28cm,△ABC的周长
是22cm, 则AC的长为( )A. 6cm B. 12cm C. 4cm D. 8cmABDCADBC4. 如图,在 ABCD中,∠A:∠B=7:2,
则∠C的度数是 . D1400EABDC9cm5cm5.如图,在 ABCD中,若BE平分∠ABC,
则ED= .4cm25cm5cm4cm16.如图,在 ABCD中,CE⊥AB,点E为垂足,
如果∠A=125°,则∠BCE的度数为 .ADBCE3507.已知 ABCD,延长AB到E, 延长CD到F ,使
BE=DF. 求证:AF=CEABDCFE证明:
∵ ABCD
∴AD=CB,∠1= ∠2
∴ 1800-∠1= 1800- ∠2,即∠3= ∠4
又∵ DF=BE
∴△AFD≌△CEB(SAS)
∴AF=CE1234 8. 已知如图:E、F是平行四边形ABCD的对角线
AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF1234证明:(1)
∵平行四边形ABCD中,AD∥CB
∴AD=CB,∠1=∠2
∵ AE=CF ∴ AE+EF=CF+EF,即AF=CE
∴△AFD≌△CEB(SAS)
(2) ∵△AFD≌△CEB
∴∠3=∠4
∴ DF∥EB 如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM2.平行四边形的对边相等;3.平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形1.平行四边形的对边平行;∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC小结:平行四边形的性质是证明线段相等和 角相等的重要依据和方法。平行四边形的性质∴AB=CD,AD=BC∴∠A=∠C,∠B=∠DABDCE9cm5cm活动 4运用所学知识解决问题如果 ∠C= 100° ,求∠BED= ? 2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .58°2832122°活动 528323.求如图所示的四边形ABCD的面积.3cm活动 6BADC302050° 50°130°100 首页上页下页 如图,在 ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长度?FDCBAE活动与探究首页上页下页问题1 :在 ABCD中,已知∠A =32。,求其余三个角的度数。∵四边形ABCD是平行四边形解:且 ∠A =32。 (已知)∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等) 又∵AD∥BC(平行四边形的对边平行)∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。说一说 ∠C=80°∠D=100°∠B=100°在 ABCD 中, ∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。48°3cm132°说一说2 通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结课堂回顾:1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°互相平分AO=CO BO=DO
读作:平行四边形ABCD2.平行四边形不相邻的两个顶点连成的线段叫 平行四边形的对角线.3.平行四边形相对的边称为对边,相对的角称为对角平行四边形相关概念对边:AB与CD; BC与DA.对角: ∠ABC与∠CDA; ∠BAD与∠DCB.两组对边分别平行的四边形叫做平行四边形.∴四边形ABCD是平行四边形∵四边形ABCD是平行四边形AB∥CDAD∥BC∴ 理解定义ABCD①②ABCD 平行四边形的边、角有怎样的数量关系?猜一猜平行四边形的对边平行.
平行四边形的对边相等.
平行四边形的对角相等.平行四边形的邻角互补.ABCD平行四边形的性质如何证明即∠BAD=∠DCB证明:连结AC ∵AB∥CD,AD∥BC(平行四边形的对边平行)∴∠1=∠2,∠3=∠4∴ △ABC≌△CDA(ASA)∴AB=CD,BC=DA,∠B=∠D又∵∠1=∠2,∠3=∠4∴∠1+∠4=∠2+∠3在△ABC和△CDA中ABCD求证: AB=CD,BC=DA;∠B=∠D,∠BAD=∠DCB方法小结:
有关四边形的问题常常
可转化为三角形问题来
处理。平行四边形的性质几何语言:定理1:平行四边形的两组对边分别相等∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC(平行四边形的对边相等)∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 定理2:平行四边形的两组对角分别相等∴ ∠A+∠B=180°,∠B+∠C=180°∵ 四边形ABCD是平行四边形∴ AB∥CD,AD ∥ BC(平行四边形的对边平行) 1.如图:在 ABCD中,根据已知你能得到哪
些结论?为什么?32cm30cm56°124°124°小结:平行四边形中知道其中一角可求出另外三个角的度数。
知道两边可求另外两边的长度。小试牛刀 例题教学: ? 例1 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?解:∵四边形ABCD是平行四边形∵ AB=8∴∴∴答:其他三条边各长8m,10m,10m.8m8m有一块形状如图 所示的玻璃,不小心把EDF部分打碎了,现在只测得AE=60cm,BC=80cm,∠B=60°且AE∥BC、AB∥CF,你能根据测得的数据计算出DE的长度和∠D的度数吗?解决问题60cm80cm600∠D= ∠B=600DE= 80-60=20(cm) 用两个全等的三角形纸片可以拼出几种形状不同的平行四边形?拼一拼从拼图可以得到什么启示?小结:
平行四边形可以是由两个全等的三角形组成,因此在解决平行四边形的问题时,通常可以连结对角线转化为两个全等的三角形进行解题。 随堂练习: 401. 在 ABCD 中,AD=40,CD=30,
∠B=60°,则BC= ; AB= ;
∠A= , ∠C= , ∠D= .30120°120°60°403060°2. 在 ABCD 中,∠ADC=120°,
∠CAD=20°,则
∠ABC= , ∠CAB= .120°40°20°120°20°20°3.如图, ABCD的周长是28cm,△ABC的周长
是22cm, 则AC的长为( )A. 6cm B. 12cm C. 4cm D. 8cmABDCADBC4. 如图,在 ABCD中,∠A:∠B=7:2,
则∠C的度数是 . D1400EABDC9cm5cm5.如图,在 ABCD中,若BE平分∠ABC,
则ED= .4cm25cm5cm4cm16.如图,在 ABCD中,CE⊥AB,点E为垂足,
如果∠A=125°,则∠BCE的度数为 .ADBCE3507.已知 ABCD,延长AB到E, 延长CD到F ,使
BE=DF. 求证:AF=CEABDCFE证明:
∵ ABCD
∴AD=CB,∠1= ∠2
∴ 1800-∠1= 1800- ∠2,即∠3= ∠4
又∵ DF=BE
∴△AFD≌△CEB(SAS)
∴AF=CE1234 8. 已知如图:E、F是平行四边形ABCD的对角线
AC上的两点,AE=CF
求证:(1)△ADF≌ △CBE (2)EB∥DF1234证明:(1)
∵平行四边形ABCD中,AD∥CB
∴AD=CB,∠1=∠2
∵ AE=CF ∴ AE+EF=CF+EF,即AF=CE
∴△AFD≌△CEB(SAS)
(2) ∵△AFD≌△CEB
∴∠3=∠4
∴ DF∥EB 如图 在?ABC中,AD平分∠BAC,点M,E,F分别
是AB,AD,AC上的点,四边形BEFM是平行四边形
求证:AF=BM
BDCEFAM 证明: ∵ 四边形BEFM是平行四边形
∴BM=EF AB//EF
∵ AD平分∠BAC
∴∠BAD=∠CAD
∵AB//EF ∴ ∠BAD=∠AEF
∴∠CAD =∠AEF ∴ AF=EF
∴ AF=BM2.平行四边形的对边相等;3.平行四边形的对角相等;
∵四边形ABCD是平行四边形∵四边形ABCD是平行四边形1.平行四边形的对边平行;∵四边形ABCD是平行四边形∴AB∥CD,AD∥BC小结:平行四边形的性质是证明线段相等和 角相等的重要依据和方法。平行四边形的性质∴AB=CD,AD=BC∴∠A=∠C,∠B=∠DABDCE9cm5cm活动 4运用所学知识解决问题如果 ∠C= 100° ,求∠BED= ? 2.如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= , BC = .58°2832122°活动 528323.求如图所示的四边形ABCD的面积.3cm活动 6BADC302050° 50°130°100 首页上页下页 如图,在 ABCD中,AB=4cm,AD=7cm,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长度?FDCBAE活动与探究首页上页下页问题1 :在 ABCD中,已知∠A =32。,求其余三个角的度数。∵四边形ABCD是平行四边形解:且 ∠A =32。 (已知)∴ ∠A = ∠C=32。, ∠B= ∠D (平行四边形的对角相等) 又∵AD∥BC(平行四边形的对边平行)∴ ∠A + ∠B =180。(两直线平行,
同旁内角互补)∴ ∠B= ∠D= 180。- ∠A = 180。- 32。=148。解:∵四边形ABCD是平行四边形(已知)
∴AB=CD,BC=AD(平行四边形的对边相等)
又∵AB=6cm,BC=4cm(已知)
∴AB=CD= 6cm,BC=AD= 4cm已知 ABCD中,∠A=80°,你能求出其他各角的度数吗?说说你的理由。说一说 ∠C=80°∠D=100°∠B=100°在 ABCD 中, ∠A=48°,BC=3cm,则∠B= , ∠C= ,AD= 。48°3cm132°说一说2 通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结通过本节课的学习,你有什么收获?1.两组对边分别平行的四边形叫做平行四边形.
2.平行四边形的性质:对边平行
对边相等
对角相等
邻角互补
3.解决平行四边形的有关问题经常连结对角线转化为三角形。课堂小结课堂回顾:1:定义:两组对边分别平行的四边形叫做平行四边形.
2:性质:平行四边形的对边平行。
平行四边形的对边相等。
平行四边形的对角相等。
平行四边形的邻角互补。
3:性质的运用平行四边形的性质平行且相等相等互补∠A=∠C,∠B=∠D∠A+∠B=180°互相平分AO=CO BO=DO
