天津市梅江中学八年级数学下册 18.1.2 平行四边形的判定课件2
文档属性
| 名称 | 天津市梅江中学八年级数学下册 18.1.2 平行四边形的判定课件2 |  | |
| 格式 | zip | ||
| 文件大小 | 304.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-07-02 17:14:25 | ||
图片预览





文档简介
课件24张PPT。18.1.2平行四边形的判定(2)复习巩固 1.平行四边形的性质:
边_____________,___________________
角______________
对角线_____________
2.判定一个四边形是平行四边形的四种方法:
边______________________________,
____________________________
角_______________________
对角形_____________________对边平行 对边相等
对角相等
对角线互相平分
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
1.探究并掌握平行四边形的第五种判定方法:一组对边平行且相等的四边形是平行四边形,并且能够根据判定方法进行相关的应用。
2.了解三角形的中位线及其性质,并会简单的应用。
3.在探索过程中发展合理的推理意识、主动探究的习惯和如何添加辅助线的思想。
学习目标设置情境
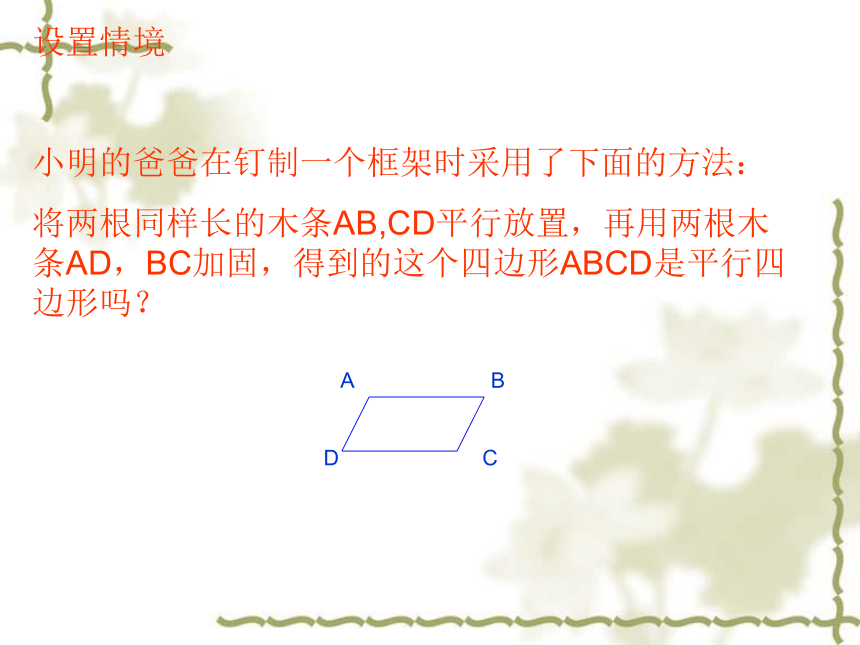
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是平行四边形吗? A B
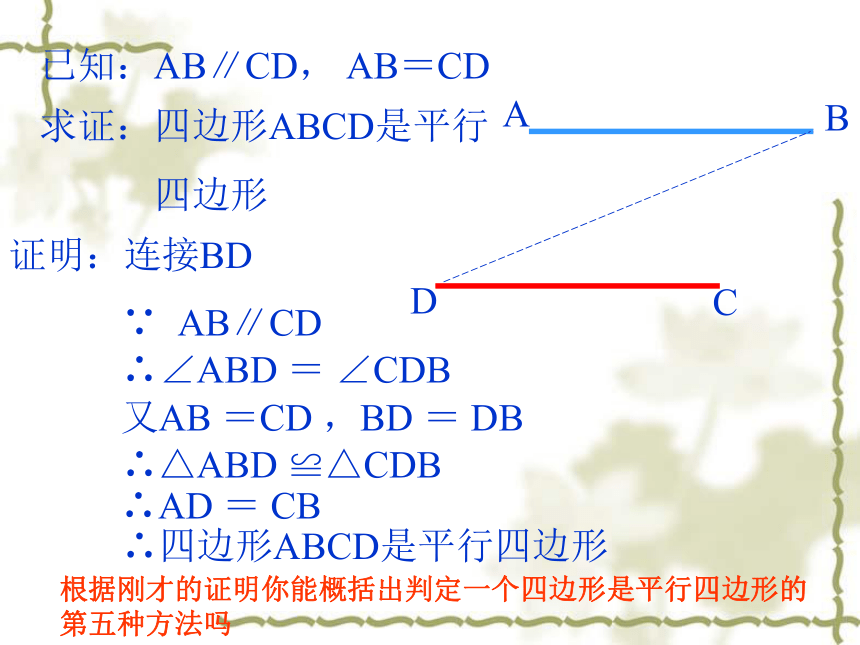
D C已知:AB∥CD, AB=CD求证:四边形ABCD是平行
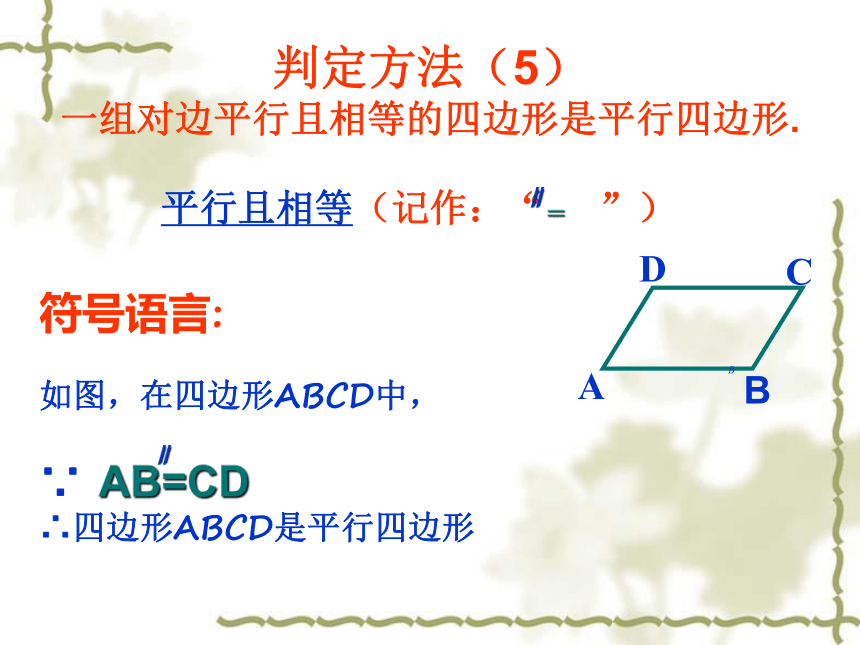
四边形证明:连接BD根据刚才的证明你能概括出判定一个四边形是平行四边形的第五种方法吗判定方法(5) 一组对边平行且相等的四边形是平行四边形. 符号语言:如图,在四边形ABCD中,
∵ AB=CD
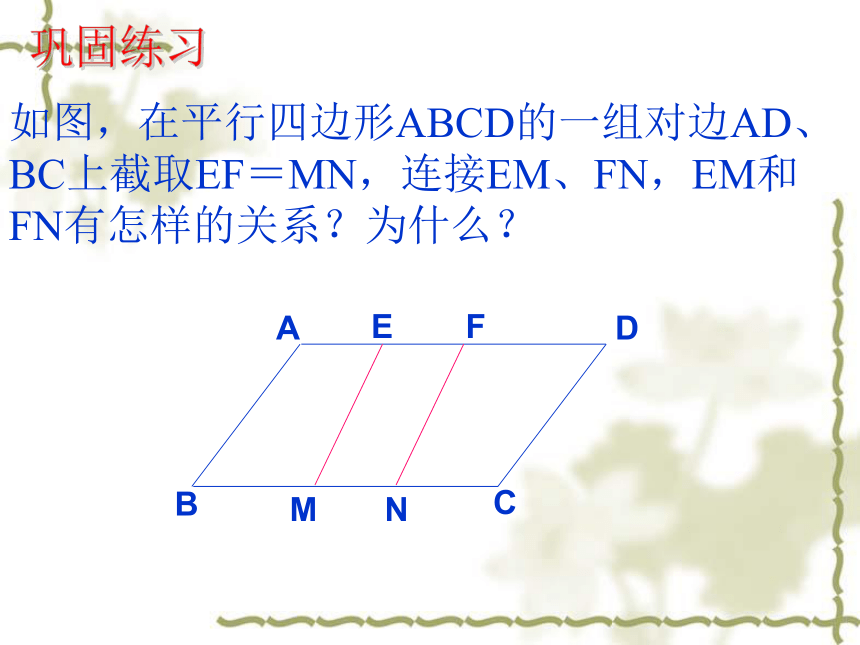
∴四边形ABCD是平行四边形∥平行且相等(记作:“= ”) ∥从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习
自学课本P.89第8,9两行,解答下列问题。
1、 叫做三角形的中位线,一个三角形有 条中位线。
2.在练习本上画出一个三角形,并画出它的一条中位线。连接三角形两边中点的线段三自主学习三角形的中位线有什么性质?如图,EF是△ABC 的一条中位线. (1)量一量DE,BC的长是多少?你能作出什么猜测? (2)观察图形中的EF与BC,猜测DE 与BC 位置关系吗?几何画板验证一下
探究与思考怎样将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?(1)剪一个三角形,记为△ABC;(2)沿中位线DE将△ABC剪成两部分,并将△ADE绕点E顺时针旋转180°得四边形BCFD. ABCDEF四边形BCFD是平行四边形吗? 为什么?四边形BCFD是平行四边形ABCDEF∵DE=EF ∠1=∠2 AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB
∴BD∥ CF且 BD =CF
∴四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC 已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。 12ABCEDFCEDFBA
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。 用符号语言表示∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.数量关系位置关系 (1)证明平行
(2)证明一条线段是另一条线
段的2倍或ABCDE 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线定理的主要用途:巩固新知
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4ABCDED 8cm6cm 平行于
等于 一半 4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = . 61°24 5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .5㎝ 6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
5.27、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。12EFBACD 知识总结:
1。判定定理:一组对边平行且相等的四边形是平行四边形
2.定义 :连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。数学思想:转化思想
1.把四边形的问题转化为三角形问题解决
2.线段的倍分问题可转化为相等问题来解决.
数学方法:在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法本节课你有哪些收获?已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。挑战自我
边_____________,___________________
角______________
对角线_____________
2.判定一个四边形是平行四边形的四种方法:
边______________________________,
____________________________
角_______________________
对角形_____________________对边平行 对边相等
对角相等
对角线互相平分
两组对边分别平行的四边形是平行四边形
两组对边分别相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
对角线互相平分的四边形是平行四边形
1.探究并掌握平行四边形的第五种判定方法:一组对边平行且相等的四边形是平行四边形,并且能够根据判定方法进行相关的应用。
2.了解三角形的中位线及其性质,并会简单的应用。
3.在探索过程中发展合理的推理意识、主动探究的习惯和如何添加辅助线的思想。
学习目标设置情境
小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是平行四边形吗? A B
D C已知:AB∥CD, AB=CD求证:四边形ABCD是平行
四边形证明:连接BD根据刚才的证明你能概括出判定一个四边形是平行四边形的第五种方法吗判定方法(5) 一组对边平行且相等的四边形是平行四边形. 符号语言:如图,在四边形ABCD中,
∵ AB=CD
∴四边形ABCD是平行四边形∥平行且相等(记作:“= ”) ∥从边来判定1、两组对边分别平行的四边形是平行四边形 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形理一理平行四边形的判定方法如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习
自学课本P.89第8,9两行,解答下列问题。
1、 叫做三角形的中位线,一个三角形有 条中位线。
2.在练习本上画出一个三角形,并画出它的一条中位线。连接三角形两边中点的线段三自主学习三角形的中位线有什么性质?如图,EF是△ABC 的一条中位线. (1)量一量DE,BC的长是多少?你能作出什么猜测? (2)观察图形中的EF与BC,猜测DE 与BC 位置关系吗?几何画板验证一下
探究与思考怎样将一个三角形纸片剪成两部分,使分成的两部分能拼成一个平行四边形?(1)剪一个三角形,记为△ABC;(2)沿中位线DE将△ABC剪成两部分,并将△ADE绕点E顺时针旋转180°得四边形BCFD. ABCDEF四边形BCFD是平行四边形吗? 为什么?四边形BCFD是平行四边形ABCDEF∵DE=EF ∠1=∠2 AE=EC
∴△ADE ≌ △CFE证明:如 图,延 长DE 到 F,使EF=DE ,连 结CF.∴AD=FC 、∠A=∠ECF
∴AB∥FC又AD=DB
∴BD∥ CF且 BD =CF
∴四边形BCFD是平行四边形还有另外的证法吗?∴DF∥BC,DF=BC又∵即DE∥BC 已知:在△ABC 中,DE是△ABC 的中位线
求证:DE ∥ BC,且DE= BC 。 12ABCEDFCEDFBA
三角形中位线定理
三角形的中位线平行于第三边,且等于第三边的一半。 用符号语言表示∵DE是△ABC的中位线
∴ DE∥BC,
DE= BC.数量关系位置关系 (1)证明平行
(2)证明一条线段是另一条线
段的2倍或ABCDE 三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.三角形的中位线定理的主要用途:巩固新知
1.三角形的中位线_______第三边,并且______第三边的____________
2.如图:在△ABC中,DE是中位线。
(1)若∠ADE=60°,则∠B= ;
(2)若BC=8cm,则DE= cm.
(3)DE +BC=12cm,则BC=——
3.若等腰△ABC的周长是40cm,AB=AC=14cm,则中位线DE=———60°4ABCDED 8cm6cm 平行于
等于 一半 4.如图, MN 为△ABC 的中位线,若∠ABC =61°则∠AMN = ,
若MN =12 ,则BC = . 61°24 5. 如图, △ABC 中, D ,E 分别为AB,
AC 的中点,当BC =10㎝时,则DE = .5㎝ 6.如图,已知△ABC中,
AB = 3㎝,BC=3.4 ㎝ AC=4㎝ 且D,E,F分别为 AB,BC,AC边的中点,则△DEF的周长
是 ㎝.
5.27、如下图:在Rt △ ABC中,∠A=90°,D、E、F分别是各边中点, AB=6cm,AC=8cm,则△DEF的周长= cm。12EFBACD 知识总结:
1。判定定理:一组对边平行且相等的四边形是平行四边形
2.定义 :连接三角形两边中点的线段叫做三角形的中位线
3.三角形的中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半。数学思想:转化思想
1.把四边形的问题转化为三角形问题解决
2.线段的倍分问题可转化为相等问题来解决.
数学方法:在三角形的中位线定理的发现过程用到画图、测量、猜想、验证、证明等数学方法本节课你有哪些收获?已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点。
求证:四边形EFGH是平行四边形。挑战自我
